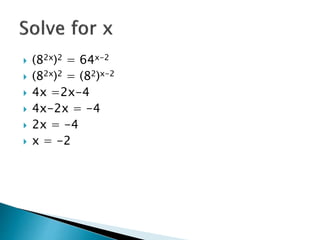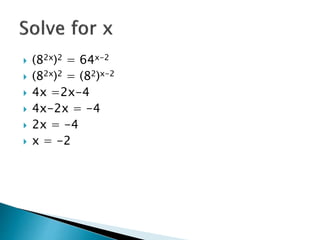
The document discusses indices and the laws of indices. It explains that indices provide a compact way to write repeated multiplication and that understanding indices is essential for algebraic processes. It then describes the three main laws of indices: 1) when expressions with the same base are multiplied, the indices are added, 2) when expressions with the same base are divided, the indices are subtracted, and 3) when two indices are multiplied, the new index is the product of the original indices. It provides examples of applying each law.

1. Trevor Bennett

2.  Indices is a more compact way of expressing
an algebraic notation for repeated
multiplication of the same number or
variable. Great space saver!

3.  A knowledge indices is essential for an
understanding of most algebraic processes.
 To manipulate expressions involving indices
we use rules known as the laws of indices.
 There are essentially three laws.
 The laws should be used precisely as they are
stated:
 Do not make up variations of your own!

4.  When expressions with the same base are
multiplied, the indices are added.
 i.e. am x an = am+n
 For example:
 105 x102= 105+2 =107

5.  When expressions with the same base are
divided, the indices are subtracted.
 i.e. am/an = am-n
 Example: We can write
 85/83 =85-3 =82
 Z7/z3 = z7-3= z4
Also if you have 1/an =a-n
and if you have 1/a-m =am

6. When two indices m and n have been multiplied
to yield the new index mn
i.e. (am)n = amn
Example:

7.  It is useful to note that any base raise to
power of zero is equal to one
 i.e. a0 = 1
 For example if you put all of these in your
calculator, you will get the same result of
one:
 90, 30,100,340, 670,990, 1550

8.  And any base raise to power of one is equal
to base. i.e. a1 = a

9.  If (ex-2)2 = e3x-5, find x.
 Equating the indices, we get
 (x-2)2 =3x – 5
 2x -4 =3x-5
 Therefore x = 1

10.  (82x)2 = 64x-2
 (82x)2 = (82)x-2
 4x =2x-4
 4x-2x = -4
 2x = -4
 x = -2