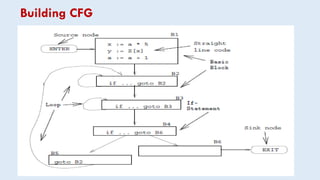
Intermediate representations are used in compilers to represent programs between the source and target languages. Control flow graphs (CFG) are a common intermediate representation that represent a program as a directed graph with basic blocks as nodes and edges showing possible control transfers. CFGs help optimize programs by breaking them into manageable blocks and making structures like loops and branches explicit. Building a CFG involves identifying basic blocks, which are straight line code sequences without internal jumps, and representing the control flow between them.

1. Intermediate Representations
Control Flow Graphs (CFG)
Don by khalid alsediri
COMP2105

2. Intermediate Representations(IR)
An intermediate representation is a representation of a program
part way between the source and target language
.
IR use many technique for representation
-Structured (graph or tree-based)
-Flat, tuple-based
-Flat, stack-based
-Or any combination of the above three

3. Optimization
Code transformations to improve program
-minimize execution time.
-reduce program size .
Must be save, the result program should give same
result to all possible input

4. Control Flow Graphs(CFG)
A control flow graph (CFG) is a data structure for High level
representation or low level representation .
1. break the big problem into smaller piece which are
manageable
2. To perform machine independent optimizations
3. Can easily find unreachable code
4. Makes syntactic structure (like loops) easy to find
The CFG is a directed graph where the vertices represent
basic blocks and edges represent possible transfer of control
flow from one basic block to another

5. Building CFG
• We divide the intermediate code of each procedure into basic
blocks. A basic block is a piece of straight line code, i.e. there
are no jumps in or out of the middle of a block.
• The basic blocks within one procedure are organized as a
(control) flow graph, or CFG. A flow-graph has
• basic blocks 𝑩 𝟏· · · 𝑩 𝒏 as nodes,
• a directed edge 𝑩 𝟏 𝑩 𝟐 if control can flow from 𝑩 𝟏 to 𝑩 𝟐.
• Special nodes ENTER and EXIT that are the source and sink
of the graph.
• Inside each basic block can be any of the IRs we’ve seen:
tuples, trees, DAGs, etc.

6. Building CFG

7. Building the CFG
• High-level representation
– Control flow is implicit in an AST.
• Low-level representation:
– Nodes represent statements (low-level linear IR)
– Edges represent explicit flow of control

8. • Program
x = z-2 ;
y = 2*z;
if (c) {
x = x+1;
y = y+1;
}
else {
x = x-1;
y = y-1;
}
z = x+y;
x = z-2 ;
y = 2*z;
if (c)
x = x+1;
y = y+1;
x = x-1;
y = y-1;
z = x+y;
B3
B1
B2
B4
FT
Example high level

9. 1 a := 0
2 b := a * b
3 L1: c := b/d
4 if c < x goto L2
5 e := b / c
6 f := e + 1
7 L2: g := f
8 h := t - g
9 if e > 0 goto L3
10 goto L1
11 L3: return
a := 0
b := a * b
c := b/d
if c < x
e := b / c
f := e + 1
g := f
h := t - g
if e > 0
goto return
B1
B2
B3
B4
B6 B5
Low level example

10. ---------Source Code-----------------------
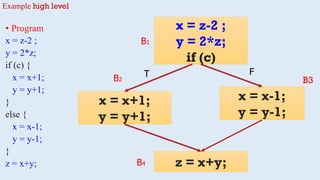
X := 20; WHILE X < 10 DO
X := X-1; A[X] := 10;
IF X = 4 THEN X := X - 2; ENDIF;
ENDDO; Y := X + 5;
---------Intermediate Code---------------
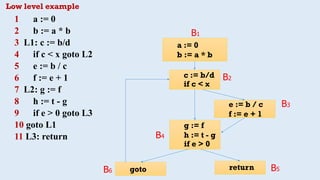
(1) X := 20
(2) if X>=10 goto (8)
(3) X := X-1
(4) A[X] := 10
(5) if X<>4 goto (7)
(6) X := X-2
(7) goto (2)
(8) Y := X+5
X := 20
Y := X+5
goto B2
X := X-2
X := X-1
(4) A[X] := 10
(5) if X<>4 goto B6
if X>=10 goto B4
B1
B2
B4B3
B5
B6

11. Building basic blocks algorithm
• Identify leaders
1-The first instruction in a procedure, or
2-The target of any branch, or
3-An instruction immediately following a branch (implicit target)
• For each leader, its basic block is the leader
and all statements up to, but not including, the
next leader or the end of the program.

12. Building basic blocks algorithm
• Input: List of n instructions (instr[i] =𝑖 𝑡ℎ instruction),
A sequence of intermediate code statements
Output: Set of leaders & list of basic blocks
(block[x] is block with leader x)
leaders = {1} // First instruction is a leader
for i = 1 to n // Find all leaders
if instr[i] is a branch
leaders = leaders ∪ set of potential targets of instr[i]
foreach x ∈ leaders //each leader is leader of it self
block[x] = { x }
i = x+1 // Fill out x’s basic block
while i ≤ n and i ∉ leaders
block[x] = block[x] ∪ { i }
i = i + 1

13. Building basic blocks algorithm
1 a := 0
2 b := a * b
3 L1: c := b/d
4 if c < x got L2
5 e := b / c
6 f := e + 1
7 L2: g := f
8 h := t - g
9 if e > 0 goto L3
10 goto L1
11 L3: return

14. Building basic blocks algorithm
1 a := 0
2 b := a * b
3 L1: c := b/d
4 if c < x got L2
5 e := b / c
6 f := e + 1
7 L2: g := f
8 h := t - g
9 if e > 0 goto L3
10 goto L1
11 L3: return
Leaders?
– {1, 3, 5, 7, 10, 11}
Blocks?
– {1, 2}
– {3, 4}
– {5, 6}
– {7, 8, 9}
– {10}
– {11}

15. Building CFG
• Input: A list of m basic blocks (block)
Output: A CFG where each node is a basic block
for i = 1 to m
x = last instruction of block[i]
if instr x is a branch
for each target (to block j) of instr x
create an edge from block i to block j
if instr x is not an unconditional branch
create an edge from block i to block i+1

16. Building basic blocks algorithm
1 a := 0
2 b := a * b
3 L1: c := b/d
4 if c < x got L2
5 e := b / c
6 f := e + 1
7 L2: g := f
8 h := t - g
9 if e > 0 goto L3
10 goto L1
11 L3: return
Leaders?
– {1, 3, 5, 7, 10, 11}
Blocks?
– {1, 2}
– {3, 4}
– {5, 6}
– {7, 8, 9}
– {10}
– {11}
1 a := 0
2 b := a * b
3 L1: c := b/d
4 if c < x got L2
5 e := b /
c
6 f := e +
1
7 L2: g := f
8 h := t - g
9 if e > 0 goto
L3
10 goto
L1
11 L3:
return

17. Variation of CFG
• Extended basic blocks
-A maximal sequence of instructions that
-has no merge points in it (except perhaps in the leader)
-Single entry, multiple exits
• Reverse extended basic blocks
-Useful for “backward flow” problems

18. Reference
• Modern Compilers: Theory , V. Krishna Nandivada,
2015,http://www.cse.iitm.ac.in/~krishna/courses/2015/even-
cs6013/lecture4.pdf ,accessed(19-14-2016).
• Introduction to Compilers,Tim
Teitelbaum,2008,http://www.cs.cornell.edu/courses/cs412/2008sp/l
ectures/lec24.pdf,accessed(19-14-2016).
• Modern Programming Language Implementation , E Christopher
Lewis ,2006,http://www.cis.upenn.edu/~cis570/slides/lecture03.pdf,
accessed(19-14-2016).