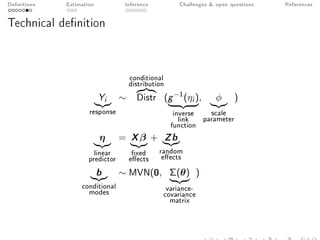
This document discusses generalized linear mixed models (GLMMs). It begins with examples of GLMM applications and definitions of key terms. The document then covers estimation methods for GLMMs, including maximum likelihood estimation, integrated likelihood, and both deterministic and stochastic approaches. Inference for GLMMs and remaining challenges are also mentioned. The overall document provides an overview of GLMM frameworks, examples, estimation techniques, and open questions.

1. Denitions Estimation Inference Challenges open questions References
Generalized linear mixed model discussion
Ben Bolker
McMaster University, Mathematics Statistics and Biology
25 April 2014

2. Denitions Estimation Inference Challenges open questions References
Acknowledgments
lme4: Doug Bates, Martin
Mächler, Steve Walker
Data: Josh Banta, Adrian Stier,
Sea McKeon, David Julian,
Jada-Simone White
NSERC (Discovery)
SHARCnet

3. Denitions Estimation Inference Challenges open questions References
Outline
1 Examples and denitions
2 Estimation
Overview
Methods
3 Inference
4 Challenges open questions

4. Denitions Estimation Inference Challenges open questions References
Outline
1 Examples and denitions
2 Estimation
Overview
Methods
3 Inference
4 Challenges open questions

5. Denitions Estimation Inference Challenges open questions References
(Generalized) linear mixed models
(G)LMMs: a statistical modeling framework incorporating:
Linear combinations of categorical and continuous
predictors, and interactions
Response distributions in the exponential family
(binomial, Poisson, and extensions)
Any smooth, monotonic link function
(e.g. logistic, exponential models)
Flexible combinations of blocking factors
(clustering; random eects)

6. Denitions Estimation Inference Challenges open questions References
(Generalized) linear mixed models
(G)LMMs: a statistical modeling framework incorporating:
Linear combinations of categorical and continuous
predictors, and interactions
Response distributions in the exponential family
(binomial, Poisson, and extensions)
Any smooth, monotonic link function
(e.g. logistic, exponential models)
Flexible combinations of blocking factors
(clustering; random eects)

7. Denitions Estimation Inference Challenges open questions References
(Generalized) linear mixed models
(G)LMMs: a statistical modeling framework incorporating:
Linear combinations of categorical and continuous
predictors, and interactions
Response distributions in the exponential family
(binomial, Poisson, and extensions)
Any smooth, monotonic link function
(e.g. logistic, exponential models)
Flexible combinations of blocking factors
(clustering; random eects)

8. Denitions Estimation Inference Challenges open questions References
Coral protection by symbionts
(McKeon et al., 2012)
none shrimp crabs both
Number of predation events
Symbionts
Numberofblocks
0
2
4
6
8
10
1
2
0
1
2
0
2
0
1
2

9. Denitions Estimation Inference Challenges open questions References
Environmental stress: Glycera cell survival
(D. Julian unpubl.)
H2S
Copper
0
33.3
66.6
133.3
0 0.03 0.1 0.32
Osm=12.8
Normoxia
Osm=22.4
Normoxia
0 0.03 0.1 0.32
Osm=32
Normoxia
Osm=41.6
Normoxia
0 0.03 0.1 0.32
Osm=51.2
Normoxia
Osm=12.8
Anoxia
0 0.03 0.1 0.32
Osm=22.4
Anoxia
Osm=32
Anoxia
0 0.03 0.1 0.32
Osm=41.6
Anoxia
0
33.3
66.6
133.3
Osm=51.2
Anoxia
0.0
0.2
0.4
0.6
0.8
1.0

10. Denitions Estimation Inference Challenges open questions References
Arabidopsis response to fertilization clipping
(Banta et al., 2010)
panel: nutrient, color: genotypeLog(1+fruitset)
0
1
2
3
4
5
unclipped clipped
qqqqq q
qq
q
qq
q
q
q
q
q
qq
q
q
qq
q
q
q
q
qqq q
q q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
qq
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
qq
q
q
q
q
q
q q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q q
q
q
q
q
q
q
q
q
q
qqq qq q
q
qq
q
qq
q
qq
q
q
q
q
qq q
q
q
q
q
q
q qqq qqq qqq qqq qq qq qq q
q
q
q
q qqq qqqq
q
q
q
qq
q
q
q q
q
q
q
qqqqqq qq
q
q
q q
q
q
q q
q
q
q
q
q
:nutrient 1
unclipped clipped
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
qq
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q q
q
q
q
q qq
q
q
q
q
q
q
q
q
qq
q
qq
q
q
q
q
q
q
q
qq
q
qq
q
q
q
q
q
q
q
q
qq
q
q
q q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
qqqq qq qqq qqqq q
q
q
qq
q
q
q
q
q
q
qqqqqqq qqq qq
q
q
q
q
q
q
q
q
q
q
q
q
q
qqqq
q
q
qqqqq
q
qq
q
q
q
q
q
q
q
q
q
q
:nutrient 8

11. Denitions Estimation Inference Challenges open questions References
Coral demography
(J.-S. White unpubl.)
Before Experimental
q
q
q q q q
qq
q
q q
q q
q
q
qq qq
q
qq q q
q
qq qq
q
qq
q
q q
qq
q
q
q
q
q
q
q
q
q
qq
q
q
q q
q
q
q
q
q q
q
q
q
q
q q
q
qqq
qq
q
q
qqqq
q qq q
q
q
q
q qq q
q
q
q
qq
q
q
q
q q q
q
q q
q q
q
q qqq qqq q
q
q
q
q
q
q
qq q
q
q
q
q
q qqq
q
q
q
q
q
q
q
q qq qqq
q
q
q
qqq
q
q
q
qq
q
qq
qq
q
qqq q
qq
qq qq qq
q
q
q
qq
q
qqq qq
q
q
q q
q
q q
q
q
q0.00
0.25
0.50
0.75
1.00
0 10 20 30 40 50 0 10 20 30 40 50
Previous size (cm)
Mortalityprobability
Treatment
q
q
Present
Removed

12. Denitions Estimation Inference Challenges open questions References
Technical denition
Yi
response
∼
conditional
distribution
Distr (g−1(ηi )
inverse
link
function
, φ
scale
parameter
)
η
linear
predictor
= Xβ
xed
eects
+ Zb
random
eects
b
conditional
modes
∼ MVN(0, Σ(θ)
variance-
covariance
matrix
)

13. Denitions Estimation Inference Challenges open questions References
What are random eects?
a way to account for among-individual, within-block correlation
a compromise between complete pooling (σ2
among = 0) and
xed eects (σ2
among → ∞)
levels selected at random from a larger population
a way do to shrinkage estimation/share information among
levels
a way to estimate variability among levels
a way to allow predictions on unmeasured levels

14. Denitions Estimation Inference Challenges open questions References
What are random eects?
a way to account for among-individual, within-block correlation
a compromise between complete pooling (σ2
among = 0) and
xed eects (σ2
among → ∞)
levels selected at random from a larger population
a way do to shrinkage estimation/share information among
levels
a way to estimate variability among levels
a way to allow predictions on unmeasured levels

15. Denitions Estimation Inference Challenges open questions References
What are random eects?
a way to account for among-individual, within-block correlation
a compromise between complete pooling (σ2
among = 0) and
xed eects (σ2
among → ∞)
levels selected at random from a larger population
a way do to shrinkage estimation/share information among
levels
a way to estimate variability among levels
a way to allow predictions on unmeasured levels

16. Denitions Estimation Inference Challenges open questions References
What are random eects?
a way to account for among-individual, within-block correlation
a compromise between complete pooling (σ2
among = 0) and
xed eects (σ2
among → ∞)
levels selected at random from a larger population
a way do to shrinkage estimation/share information among
levels
a way to estimate variability among levels
a way to allow predictions on unmeasured levels

17. Denitions Estimation Inference Challenges open questions References
What are random eects?
a way to account for among-individual, within-block correlation
a compromise between complete pooling (σ2
among = 0) and
xed eects (σ2
among → ∞)
levels selected at random from a larger population
a way do to shrinkage estimation/share information among
levels
a way to estimate variability among levels
a way to allow predictions on unmeasured levels

18. Denitions Estimation Inference Challenges open questions References
What are random eects?
a way to account for among-individual, within-block correlation
a compromise between complete pooling (σ2
among = 0) and
xed eects (σ2
among → ∞)
levels selected at random from a larger population
a way do to shrinkage estimation/share information among
levels
a way to estimate variability among levels
a way to allow predictions on unmeasured levels

19. Denitions Estimation Inference Challenges open questions References
Outline
1 Examples and denitions
2 Estimation
Overview
Methods
3 Inference
4 Challenges open questions

20. Denitions Estimation Inference Challenges open questions References
Maximum likelihood estimation
L(Yi |θ, β)
likelihood
= · · · L(Yi |β, b)
data|random eects
× L(b|Σ(θ))
random eects
db
Best t is a compromise between two components
(consistency of data with xed eects and conditional modes;
consistency of random eect with RE distribution)

21. Denitions Estimation Inference Challenges open questions References
Integrated (marginal) likelihood
−10 −5 0 5 10
0.0
0.2
0.4
0.6
0.8
1.0
conditional mode value (u)
Scaledprobability
L(b|σ2
)
L(x|b, β)
Lprod

22. Denitions Estimation Inference Challenges open questions References
Shrinkage: Arabidopsis conditional modes
q q
q
q
q
q
q q q q q q q q q q q q q q q q q q
Genotype
Mean(log)fruitset
0 5 10 15 20 25
−15
−3
0
3
q q q
q
q
q
q q q q q q q q q q q q q q q q q q
3 2 10
8
10
4
3 9 9 4 6 4 2 6 10 5 7 9 4 9 11 2 5 5

23. Denitions Estimation Inference Challenges open questions References
Estimation methods
deterministic : various approximate integrals (Breslow, 2004) . . .
stochastic (Monte Carlo): frequentist and Bayesian (Booth and
Hobert, 1999; Ponciano et al., 2009; Sung, 2007)

24. Denitions Estimation Inference Challenges open questions References
Deterministic approaches
PQL fast and biased, especially for binary/low-count data:
(MASS:glmmPQL)
Laplace intermediate (lme4:glmer, glmmML, glmmADMB,
R2ADMB (AD Model Builder))
Gauss-Hermite quadrature slow but accurate (lme4:glmer,
glmmML, repeated)
INLA Bayesian, very exible: INLA
General trade-o between exibility (ADMB/glmmADMB) and
eciency (lme4)

25. Denitions Estimation Inference Challenges open questions References
Stochastic approaches
Mostly Bayesians (Bayesian computation handles
high-dimensional integration)
various avours: Gibbs sampling, MCMC, MCEM, etc.
generally slower but more exible
simplies many inferential problems
must specify priors, assess convergence/error
specialized: glmmAK, MCMCglmm (Hadeld, 2010), bernor
general: glmmBUGS, R2WinBUGS, BRugs (WinBUGS/OpenBUGS),
R2jags, rjags (JAGS), glmer2stan, Stan

26. Denitions Estimation Inference Challenges open questions References
Estimation: example (McKeon et al., 2012)
Log−odds of predation
−6 −4 −2 0 2
Symbiont
Crab vs. Shrimp
Added symbiont
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
GLM (fixed)
GLM (pooled)
PQL
Laplace
AGQ

27. Denitions Estimation Inference Challenges open questions References
Outline
1 Examples and denitions
2 Estimation
Overview
Methods
3 Inference
4 Challenges open questions

28. Denitions Estimation Inference Challenges open questions References
Wald tests
Wald tests (e.g. typical results of summary)
based on information matrix
assume quadratic log-likelihood surface
exact for regular linear models;
only asymptotically OK for GLM(M)s
computationally cheap
approximation is sometimes awful (Hauck-Donner eect)

29. Denitions Estimation Inference Challenges open questions References
2D proles for coral predation
Scatter Plot Matrix
.sig01
2 4 6 8 101214
−3
−2
−1
0
(Intercept)
0
5
10
15
10 15
0 1 2 3
tttcrabs
−10
−8
−6
−4
−2
0
−4 −2 0
0 1 2 3
tttshrimp
−10
−8
−6
−4
−2 −6 −4 −2
0 1 2 3
tttboth
−12
−10
−8
−6
−4
−2
0 1 2 3

30. Denitions Estimation Inference Challenges open questions References
Likelihood ratio tests
better, but still have to deal with two nite-size problems:
denominator degrees of freedom (when estimating scale)
numerator is only asymptotically χ2 anyway (Bartlett
corrections)
Kenward-Roger correction? (Stroup, 2014)
Prole condence intervals: moderately expensive/fragile

31. Denitions Estimation Inference Challenges open questions References
Parametric bootstrapping
t null model to data
simulate data from null model
t null and working model, compute likelihood dierence
repeat to estimate null distribution
should be OK but ??? not well tested
(assumes estimated parameters are suciently good)

32. Denitions Estimation Inference Challenges open questions References
Parametric bootstrap results
True p value
Inferredpvalue
0.02
0.04
0.06
0.08
0.02 0.06
Osm Cu
H2S
0.02 0.06
0.02
0.04
0.06
0.08
Anoxia

33. Denitions Estimation Inference Challenges open questions References
Bayesian approaches
If we have a good sample from the posterior distribution
(Markov chains have converged etc. etc.) we get most of the
inferences we want for free by summarizing the marginal
posteriors
post hoc Bayesian can work, but mode at zero causes
problems

34. Denitions Estimation Inference Challenges open questions References
Outline
1 Examples and denitions
2 Estimation
Overview
Methods
3 Inference
4 Challenges open questions

35. Denitions Estimation Inference Challenges open questions References
On beyond R
Julia: MixedModels package
SAS: PROC MIXED, NLMIXED
AS-REML
Stata (GLLAMM, xtmelogit)
AD Model Builder
HLM, MLWiN

36. Denitions Estimation Inference Challenges open questions References
Challenges
Small/medium data: inference, singular ts (blme, MCMCglmm)
Big data: speed!
Worst case: large n, small N (e.g. telemetry/genomics)
Model diagnosis
Condence intervals accounting for uncertainty in variances
See also: http://rpubs.com/bbolker/glmmchapter, https:
//groups.nceas.ucsb.edu/non-linear-modeling/projects

37. Denitions Estimation Inference Challenges open questions References
What about space?
Sometimes blocks are spatial partitions (sites, zip codes,
states)
O-the-shelf methods for true spatial GLMMs?
(Dormann et al., 2007)
Correlation of residuals or conditional modes?
INLA; GeoBUGS; ADMB
lme4: hacking Z: pedigrees, moving average, CAR models?
lme4: flexLambda branch
methods also apply to temporal, phylogenetic correlations
(Ives and Helmus, 2011)

38. Denitions Estimation Inference Challenges open questions References
Next steps
Complex random eects:
regularization, model selection, penalized methods
(lasso/fence)
Flexible correlation and variance structures
Flexible/nonparametric random eects distributions
hybrid improved MCMC methods
Reliable assessment of out-of-sample performance

39. Denitions Estimation Inference Challenges open questions References
Banta, J.A., Stevens, M.H.H., and Pigliucci, M., 2010. Oikos, 119(2):359369. ISSN 1600-0706.
doi:10.1111/j.1600-0706.2009.17726.x.
Booth, J.G. and Hobert, J.P., 1999. Journal of the Royal Statistical Society. Series B, 61(1):265285.
doi:10.1111/1467-9868.00176.
Breslow, N.E., 2004. In D.Y. Lin and P.J. Heagerty, editors, Proceedings of the second Seattle
symposium in biostatistics: Analysis of correlated data, pages 122. Springer. ISBN 0387208623.
Dormann, C.F., McPherson, J.M., et al., 2007. Ecography, 30(5):609628.
doi:10.1111/j.2007.0906-7590.05171.x.
Hadeld, J.D., 2010. Journal of Statistical Software, 33(2):122. ISSN 1548-7660.
Ives, A.R. and Helmus, M.R., 2011. Ecological Monographs, 81(3):511525. ISSN 0012-9615.
doi:10.1890/10-1264.1.
McKeon, C.S., Stier, A., et al., 2012. Oecologia, 169(4):10951103. ISSN 0029-8549.
doi:10.1007/s00442-012-2275-2.
Ponciano, J.M., Taper, M.L., et al., 2009. Ecology, 90(2):356362. ISSN 0012-9658.
Stroup, W.W., 2014. Agronomy Journal, 106:117. doi:10.2134/agronj2013.0342.
Sung, Y.J., 2007. The Annals of Statistics, 35(3):9901011. ISSN 0090-5364.
doi:10.1214/009053606000001389.