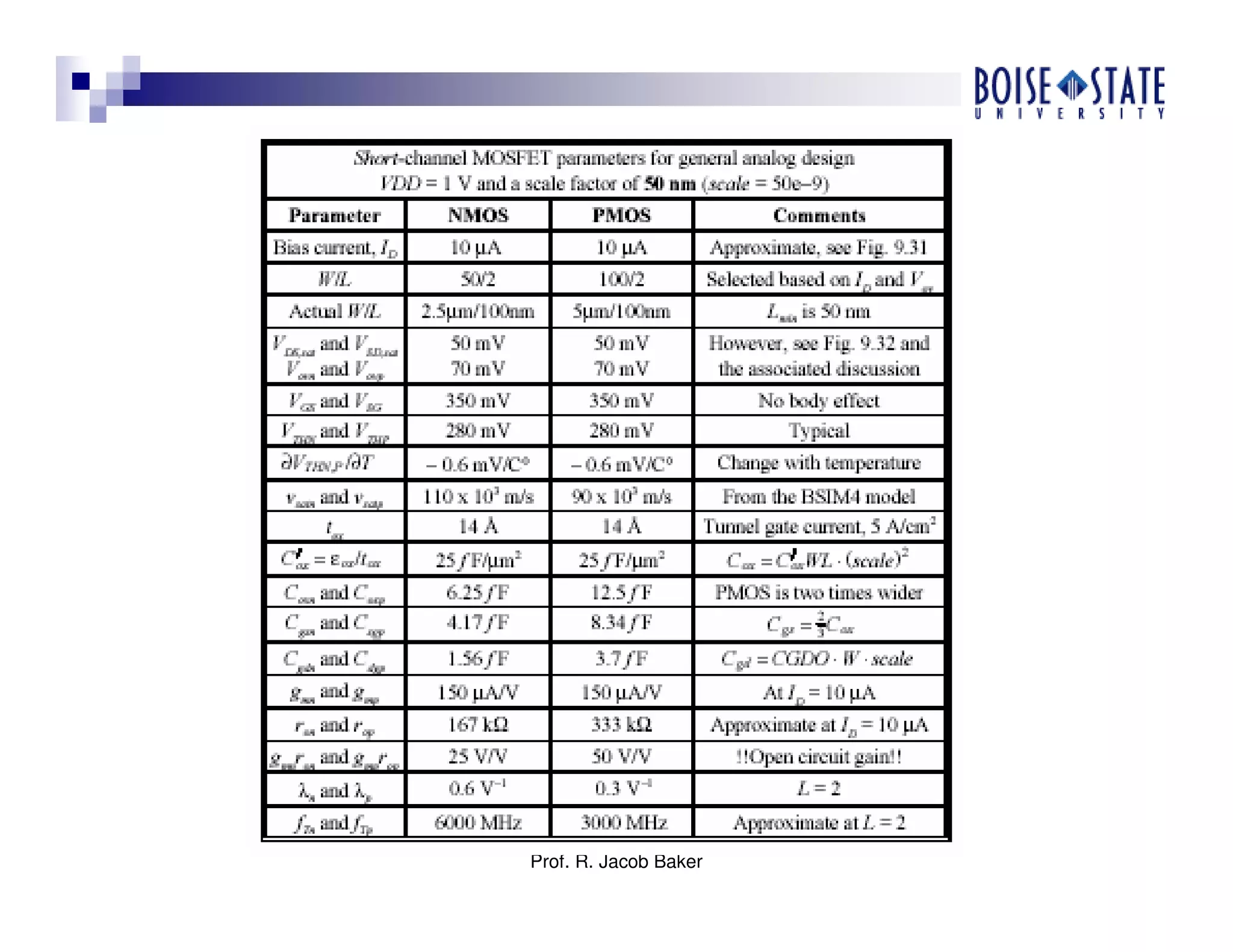
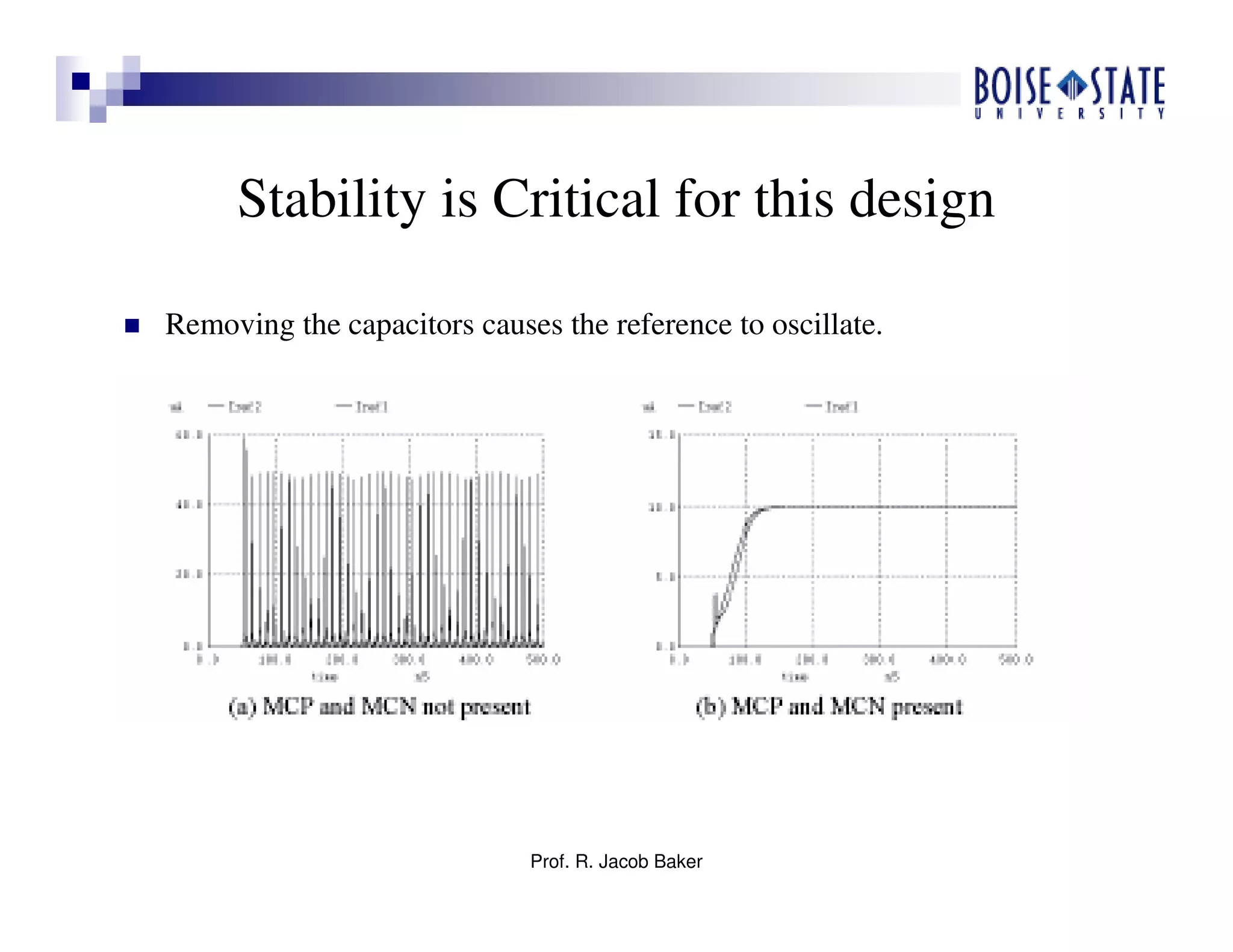
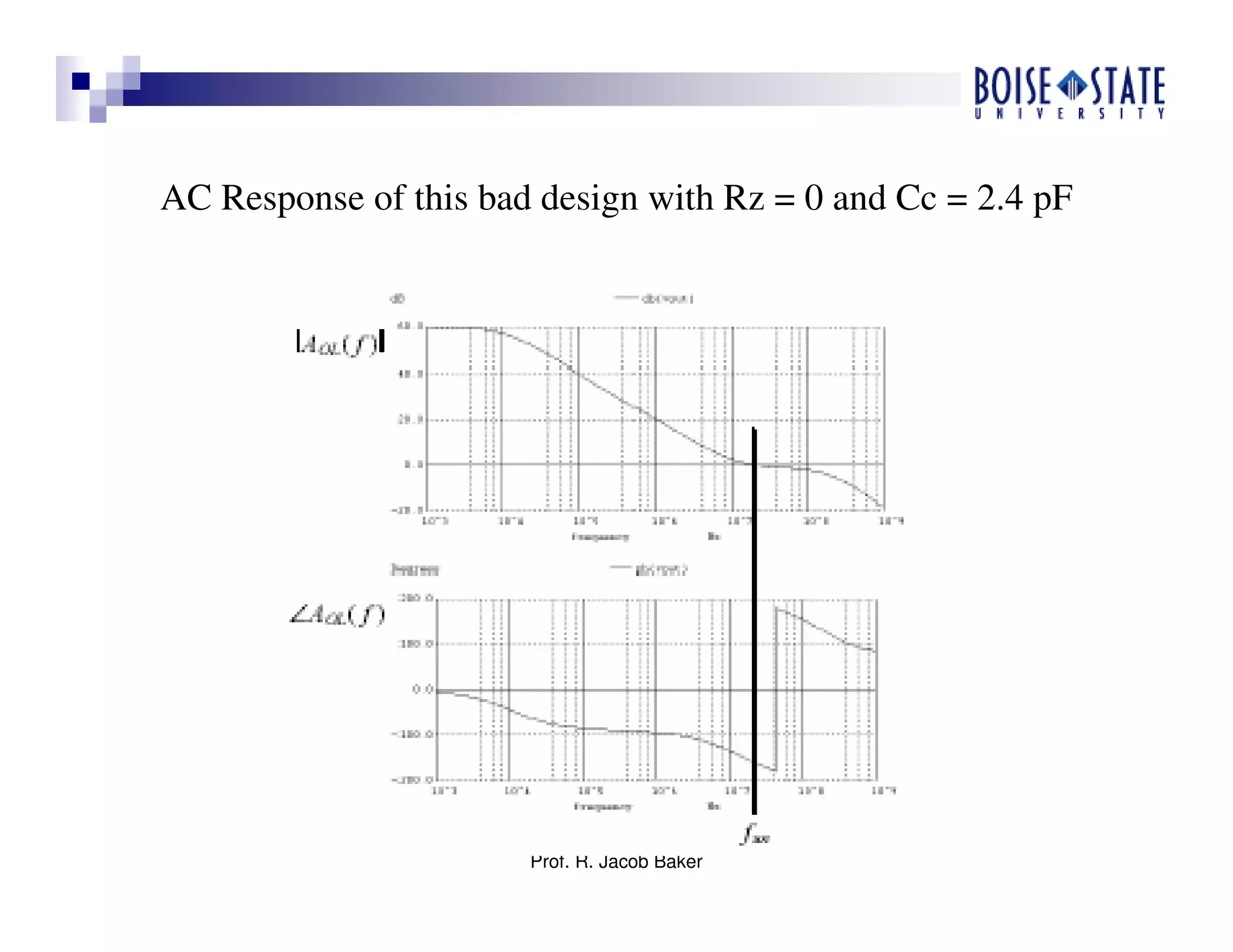
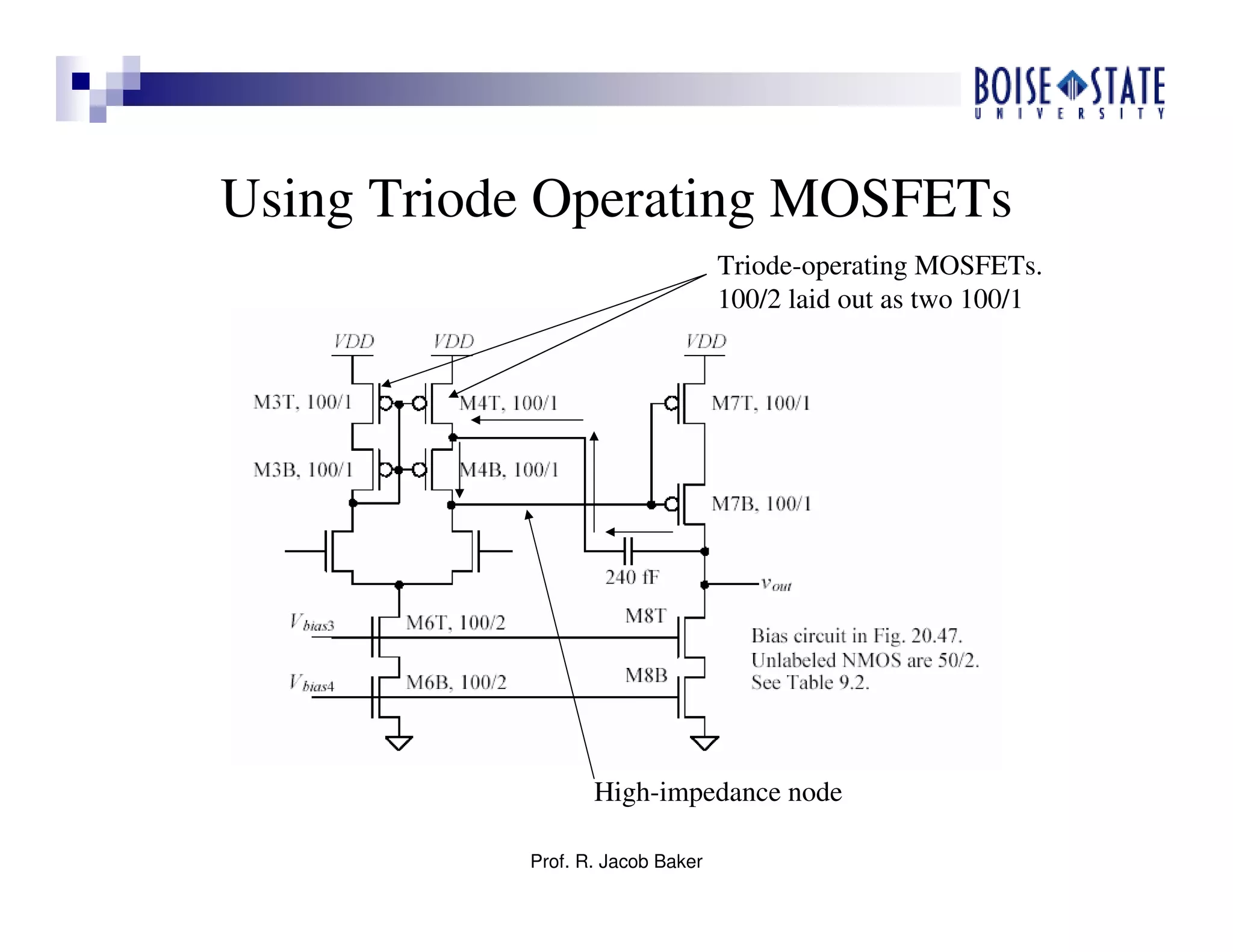
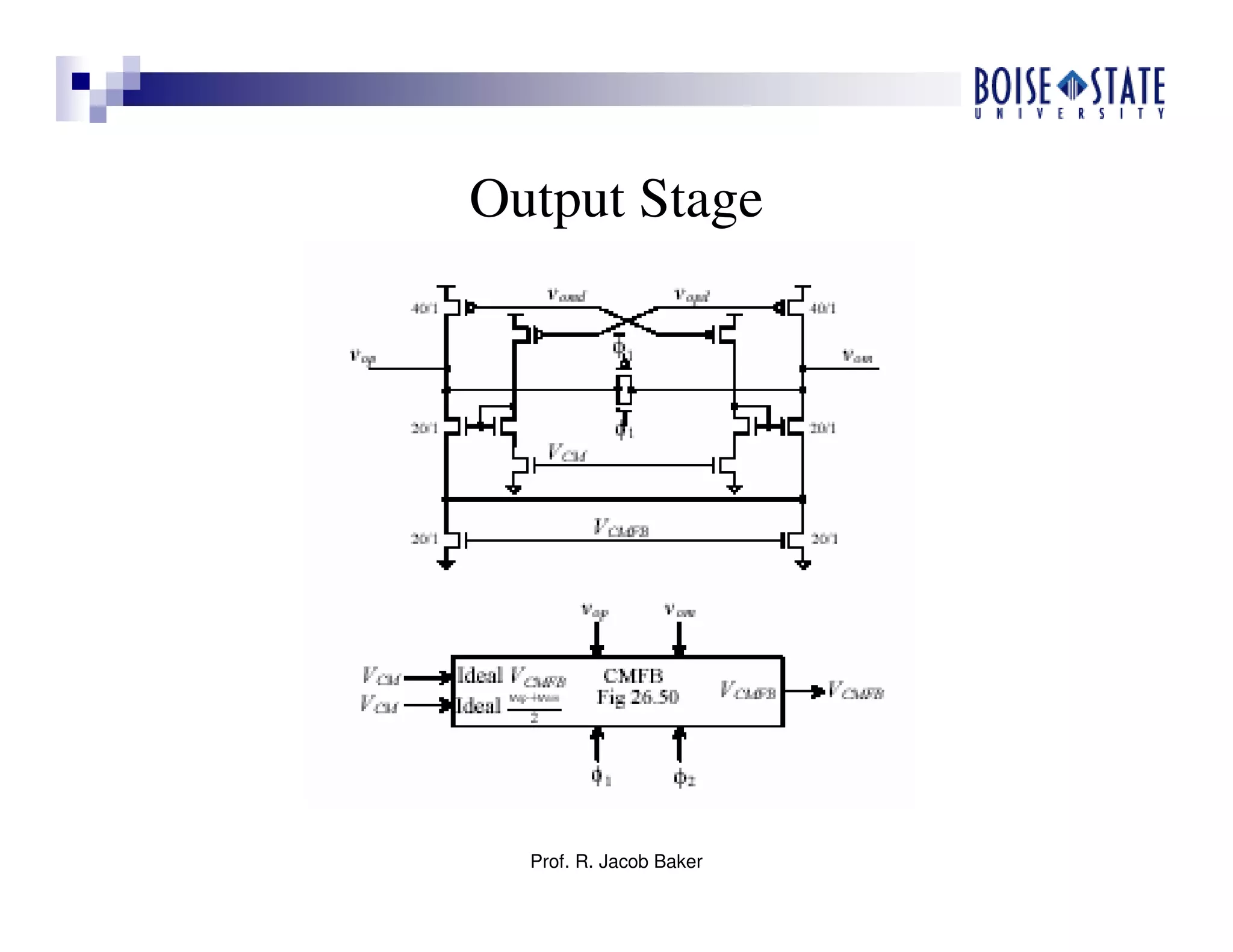
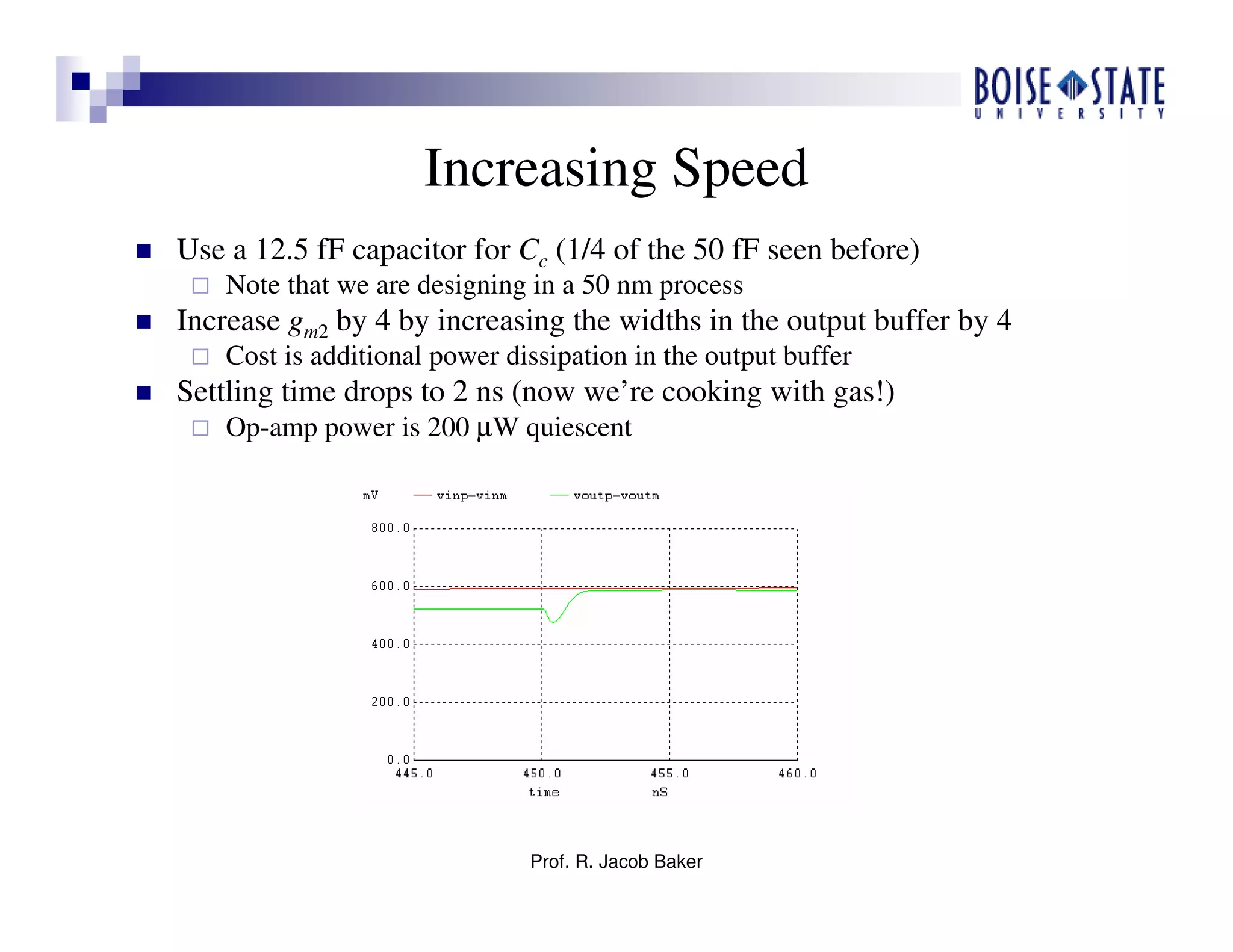
The document discusses the design of high-speed CMOS operational amplifiers for signal processing, highlighting techniques that address the challenges posed by scaling to nanometer technologies. It covers critical design aspects such as biasing, device sizing, and compensation methods while emphasizing the importance of power, speed, and manufacturability. Various design examples and practical design guidelines are provided, focusing on achieving optimal performance in CMOS op-amp applications.