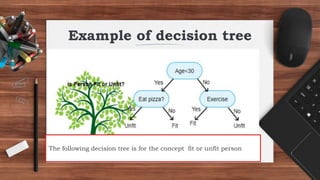
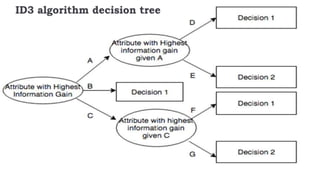
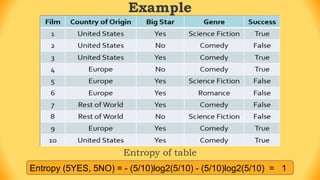
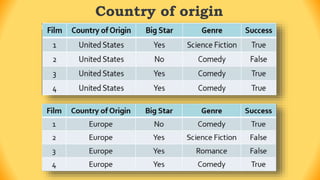
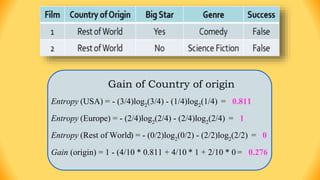
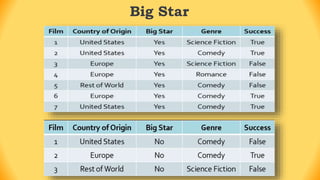
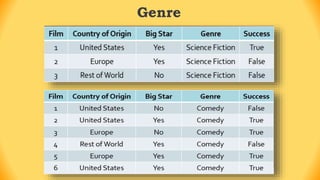
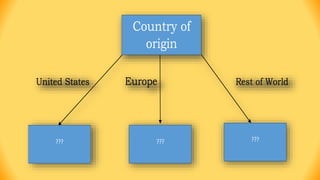
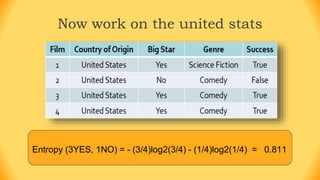
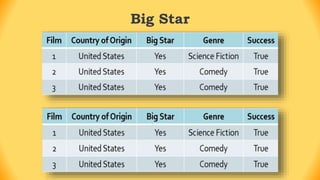
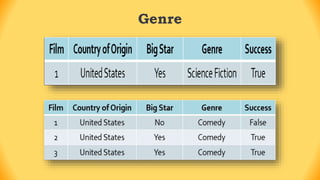
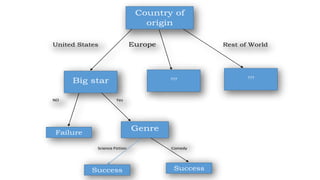
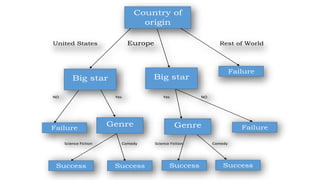
The ID3 algorithm is a decision tree learning algorithm developed by Ross Quinlan. It builds classification models in the form of a decision tree from a set of labeled training data. The algorithm works by selecting the attribute that is most useful for classifying the training examples at each step, starting with the root node. It then splits the examples into smaller subsets based on the value of that attribute. This process continues recursively on each derived subset until the subsets are pure or until stopping criteria are met. The resulting decision tree can then be used to classify new or unknown data instances.

1. ID3 Algorithm
Rehouma Cherif
Master AI and SD
02/13/2020

2. History
 Invented by Ross Quinlan in 1975.
 Quinlan was a computer science
researcher in data mining, and decision
theory.
 Received doctorate in computer science at
the University of Washington in 1968.

3. Want big impact?
Use big image.

4. What is the ID3 algorithm?
 ID3 (Iterative Dichotomiser 3).
 A mathematical algorithm for building the
decision tree.
 Algorithm used to generate a decision tree.
 The resulting tree is used to classify future
samples.
 ID3 is a precursor to the C4.5 Algorithm.
 Uses Information Theory invented by Shannon in
1948.

5. Decision Tree
 Rules for classifying data using attributes.
 Tree consists of decision nodes and decision
leafs.
 Nodes can have two or more branches which
represents the value for the attribute tested.
 Leafs nodes produces a homogeneous result.

6. Example of decision tree
The following decision tree is for the concept fit or unfit person

7. The Process
 Take the attributes and calculates their
entropies.
 Chooses attribute that has the lowest
entropy is minimum or when information
gain is maximum
 Makes a node containing that attribute

8. The Algorithm
 Create a root node for the tree.
 If all examples are positive, Return the
single-node tree Root, with label = +.
 If all examples are negative, Return the
single-node tree Root, with label = -.

9. • Else
– A = The Attribute that best classifies examples.
– Decision Tree attribute for Root = A.
– For each possible value, vi, of A,
• Add a new tree branch below Root, corresponding
to the test A = vi.
• Let Examples(vi), be the subset of examples that
have the value vi for A
• If Examples(vi) is empty
– Then below this new branch add a leaf node
with label = most common target value in the
examples
• Else below this new branch add the subtree ID3
(Examples(vi), Target_Attribute, Attributes – {A})
• End
• Return Root

10. Entropy
 Formula to calculate the homogeneity of a
sample.
 A complete homogeneous sample has an entropy
of 0
 An equally divided sample as an entropy of 1
 Entropy = - p+log2 (p+) -p-log2 (p-) for a sample of
negative and positive elements.
 to define information gain, we need to discuss
entropy first.

11. Information Gain
 Looking for which attribute creates the most
homogeneous branches
 The formula for calculating information gain is:
Gain(S, A) = Entropy(S) - ((|Sv| / |S|)*Entropy(Sv))
Where:
 Sv = subset of S for which attribute A has value v
 |Sv| = number of elements in Sv.
 |S| = number of elements in S.

12. 12

13. Entropy of table
Entropy (5YES, 5NO) = - (5/10)log2(5/10) - (5/10)log2(5/10) = 1
Example

14. Country of origin

15. Gain of Country of origin
Entropy (USA) = - (3/4)log2
(3/4) - (1/4)log2
(1/4) = 0.811
Entropy (Europe) = - (2/4)log2
(2/4) - (2/4)log2
(2/4) = 1
Entropy (Rest of World) = - (0/2)log2
(0/2) - (2/2)log2
(2/2) = 0
Gain (origin) = 1 - (4/10 * 0.811 + 4/10 * 1 + 2/10 * 0 = 0.276

16. Big Star

17. Gain of Big Star
Entropy(YES)=-(4/7)log2
(4/7)-(3/7)log2
(3/7) = 0.985
Entropy(NO)=-(1/3)log2
(1/3)-(2/3)log2
(2/3) = 0.918
Gain(Star)=1-(7/10*0.985+3/10*0.918= 0.0351

18. Genre

19. Entropy (SF) = - (1/3)log2
(1/3) - (2/3)log2
(2/3) = 0.918
Entropy (Com) = - (4/6)log2
(4/6) - (2/6)log2
(2/6) = 0.918
Entropy (Rom) = - (0/1)log2
(0/1) - (1/1)log2
(1/1) = 0
Gain (Genre) = 1 - (3/10 * 0.918 + 6/10 * 0.918 + 1/10 * 0 = 0.1738
Gain of Genre

20. Now we compare Gain
Now we compare Gain
the attention of your audience over a key
concept using icons or illustrations
Gain (Origin) = 0.276
Gain (Star) = 0.0351
Gain (Genre) = 0.1738

21. United States Europe Rest of World
Country of
origin
??? ???
???

22. Now work on the united stats
Entropy (3YES, 1NO) = - (3/4)log2(3/4) - (1/4)log2(1/4) = 0.811

23. Big Star

24. Gain of Big Star
Entropy(YES)=-(3/3)log2
(3/3)-(0/3)log2
(0/3) = 0
Entropy(NO)=-(0/1)log2
(0/1)-(1/1)log2
(1/1) = 0
Gain(Star)=1-(3/4*0+1/4*0= 0.811

25. Genre

26. Gain of Genre
Gain (Genre) = 0.1225
Gain (Star) = 0.811
The best is the star
Entropy (SF) = - (1/1)log2
(1/1) - (0/1)log2
(0/1) = 0
Entropy (Com) = - (2/3)log2
(2/3) - (1/3)log2
(1/3) = 0.918
Gain (Genre) = 1 - (1/4 * 0+ 3/4 * 0.918 = 0.1225

27. United States Europe Rest of World
NO Yes
Science Fiction Comedy
Country of
origin
Big star
???
???
Failure
Genre
Success Success

28. United States Europe Rest of World
NO Yes Yes NO
Science Fiction Comedy Science Fiction Comedy
Country of
origin
Big star Big star
Failure
Genre
Success Success
Genre
Success Success
Failure
Failure

29. Advantage of ID3
 Builds the fastest tree.
 Builds a short tree.
 Only need to test enough
attributes until all data is
classified.

30. Disadvantage of ID3
 Only one attribute at a time is
tested for making a decision.
 The modification of expert after
result.

31. Conclusion
 There exist another algorithms were
invented just after id3 has the same role
like algorithm 4.5 and algorithm cart,
ect.
 Scientific research in this domain are
search to makes a system can give a
decision tree very exact without
modification of the expert

32. Thanks!