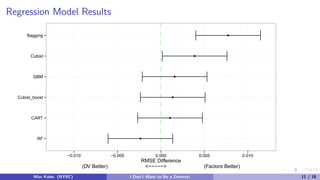
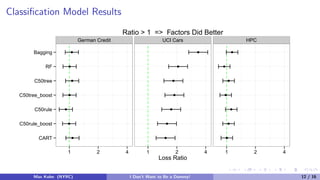
The document discusses tree-based models and the importance of encoding categorical predictors as dummy variables or factors in predictive modeling. It presents various modeling techniques and evaluates their performance on different datasets, highlighting that the choice of encoding can significantly affect model accuracy and training speed. Additionally, it concludes that the encoding decision should consider the nature of the data and the specific modeling approach used.

1. I Don’t Want to Be a Dummy!
Encoding Predictors for Trees
Max Kuhn
NYRC

2. Trees
Tree–based models are nested sets of if/else statements that make predictions in the
terminal nodes:
> library(rpart)
> library(AppliedPredictiveModeling)
> data(schedulingData)
> rpart(Class ~ ., data = schedulingData, control = rpart.control(maxdepth = 2))
n= 4331
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 4331 2100 VF (0.511 0.311 0.119 0.060)
2) Protocol=C,D,E,F,G,I,J,K,L,N 2884 860 VF (0.703 0.206 0.068 0.023) *
3) Protocol=A,H,M,O 1447 690 F (0.126 0.521 0.219 0.133)
6) Iterations< 1.5e+02 1363 610 F (0.134 0.553 0.232 0.081) *
7) Iterations>=1.5e+02 84 1 L (0.000 0.000 0.012 0.988) *
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 2 / 16

3. Rules
Similarly, rule–based models are non–nested sets of if statements:
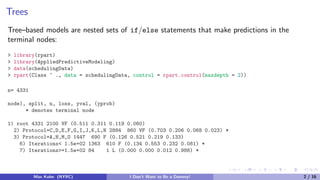
> library(C50)
> summary(C5.0(Class ~ ., data = schedulingData, rules = TRUE))
<snip>
Rule 109: (17/7, lift 9.7)
Protocol in {F, J, N}
Compounds > 818
InputFields > 152
NumPending <= 0
Hour > 0.6333333
Day = Tue
-> class L [0.579]
Default class: VF
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 3 / 16

4. Bayes!
Bayesian regression and classification models don’t really specify anything about the predictors
beyond Pr[X] and Pr[X|Y ].
If there were only one categorical predictor, we could have Pr[X|Y ] be a table of raw
probabilities:
> xtab <- table(schedulingData$Day, schedulingData$Class)
> apply(xtab, 2, function(x) x/sum(x))
VF F M L
Mon 0.1678 0.1492 0.15 0.162
Tue 0.1913 0.2019 0.27 0.255
Wed 0.2090 0.2101 0.19 0.228
Thu 0.1678 0.1589 0.18 0.154
Fri 0.2171 0.2183 0.20 0.178
Sat 0.0068 0.0082 0.00 0.023
Sun 0.0403 0.0535 0.00 0.000
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 4 / 16

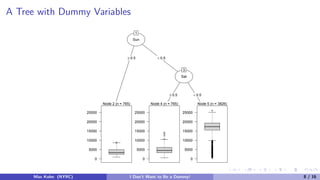
5. Dummy Variables
For the other models, we typically encode a predictor with C categories into C − 1 binary
dummy variables:
> design_mat <- model.matrix(Class ~ Day, data = head(schedulingData))
> design_mat[, colnames(design_mat) != "(Intercept)"]
DayTue DayWed DayThu DayFri DaySat DaySun
1 1 0 0 0 0 0
2 1 0 0 0 0 0
3 0 0 1 0 0 0
4 0 0 0 1 0 0
5 0 0 0 1 0 0
6 0 1 0 0 0 0
In this case, one predictor generates six columns in the design matrix
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 5 / 16

6. Encoding Choices
We make the decision on how to encode the data prior to creating the model.
That means we choose whether to present the model with the grouped categories or
ungrouped binary dummy variables.
The means we could get different representations of the model (see the next two slides).
Does it matter? Let’s do some experiments!
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 6 / 16

7. A Tree with Categorical Data
wday
1
Sun, Sat Mon, Tues, Wed, Thurs, Fri
Node 2 (n = 1530)
0
5000
10000
15000
20000
25000
q
qq
q
q
Node 3 (n = 3826)
0
5000
10000
15000
20000
25000
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qqq
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
q
qq
q
q
q
q
q
q
qqq
q
q
qq
q
q
q
q
qq
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 7 / 16

8. A Tree with Dummy Variables
Sun
1
≥ 0.5 < 0.5
Node 2 (n = 765)
0
5000
10000
15000
20000
25000
q
Sat
3
≥ 0.5 < 0.5
Node 4 (n = 765)
0
5000
10000
15000
20000
25000
q
q
q
q
Node 5 (n = 3826)
0
5000
10000
15000
20000
25000
q
q
q
q
q
q
qq
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
qqq
q
q
qq
q
q
q
q
qq
q
q
q
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
qq
q
q
q
q
q
qq
q
q
q
q
q
q
qqq
q
q
qq
qq
q
q
qq
q
q
q
q
qq
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
q
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 8 / 16

9. Data Sets
Classification:
German Credit, 13 categorical predictors out of 20 (ROC AUC ≈ 0.76)
UCI Car Evaluation, 6 of 6 (Acc ≈ 0.96)
APM High Performance Computing, 2 of 7 (κ ≈ 0.7)
Regression:
Sacramento house prices, 3 of 8 but one has 37 unique values and another has 68
(RMSE ≈ 0.13, R2 ≈ 0.6)
For each data set, we did 10 separate simulations were 20% of the data were used for testing.
Repeated cross-validation is used to the tune the models when they have tuning parameters.
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 9 / 16

10. Simulaitons
Models fit twice on each dataset (with and without dummy variables:
single trees (CART, C5.0)
single rulesets (C5.0, Cubist)
bagged trees
random forests
boosted models (SGB trees, C5.0, Cubist)
A number of performance metrics were computed for each (e.g. RMSE, binomial or
multinomial log–loss, etc.) and the test set results are used to compare models.
Confidence intervals were computed using a linear mixed model as to account for the
resample–to–resample correlation structure.
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 10 / 16

11. Regression Model Results
RF
CART
Cubist_boost
GBM
Cubist
Bagging
−0.010 −0.005 0.000 0.005 0.010
RMSE Difference
(DV Better) <−−−−−> (Factors Better)
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 11 / 16

12. Classification Model Results
German Credit UCI Cars HPC
CART
C50rule_boost
C50rule
C50tree_boost
C50tree
RF
Bagging
1 2 4 1 2 4 1 2 4
Loss Ratio
Ratio > 1 => Factors Did Better
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 12 / 16

13. It Depends!
For classification:
The larger differences in the UCI car data might indicate that, if the percentage of
categorical predictors is large, it might matter a lot.
However, the magnitude of improvement of factors over dummy variables depends on the
model.
For 2 or 3 data sets, there was no real difference.
For regression:
It doesn’t seem to matter (except when it does)
Two very similar models (bagging and random forests) showed effects in different
directions.
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 13 / 16

14. It Depends!
All of this is also dependent on how easy the problem is.
If no models are able to adequately model the data, the choice of factor vs. dummy won’t
matter.
Also, if the categorical predictors are really important, the difference would most likely be
discernible.
For the Sacramento data, ZIP code is very important. For the HPC data, the protocol variable
is also very informative.
However, one thing is definitive:
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 14 / 16

15. Factors Usually Take Less Time to Train
German Credit UCI Cars
HPC Sacramento
C50rule
C50tree
CART
C50tree_boost
C50rule_boost
RF
Bagging
Cubist_boost
Cubist
GBM
C50rule
C50tree
CART
C50tree_boost
C50rule_boost
RF
Bagging
Cubist_boost
Cubist
GBM
1 2 4 1 2 4
Speedup for Using Factors
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 15 / 16

16. R and Dummy Variables
In almost all cases, using a formula with a model function will convert factors to dummy
variables.
However, some do not (e.g. rpart, randomForest, gbm, C5.0, NaiveBayes, etc.). This
makes sense for these models.
If you are tuning your model with train, the formula method will create dummy variables and
the non–formula method does not:
> ## dummy variables presented to underlying model:
> train(Class ~ ., data = schedulingData, ...)
>
> ## any factors are preserved
> train(x = schedulingData[, -ncol(schedulingData)],
+ y = schedulingData$Class,
+ ...)
Max Kuhn (NYRC) I Don’t Want to Be a Dummy! 16 / 16