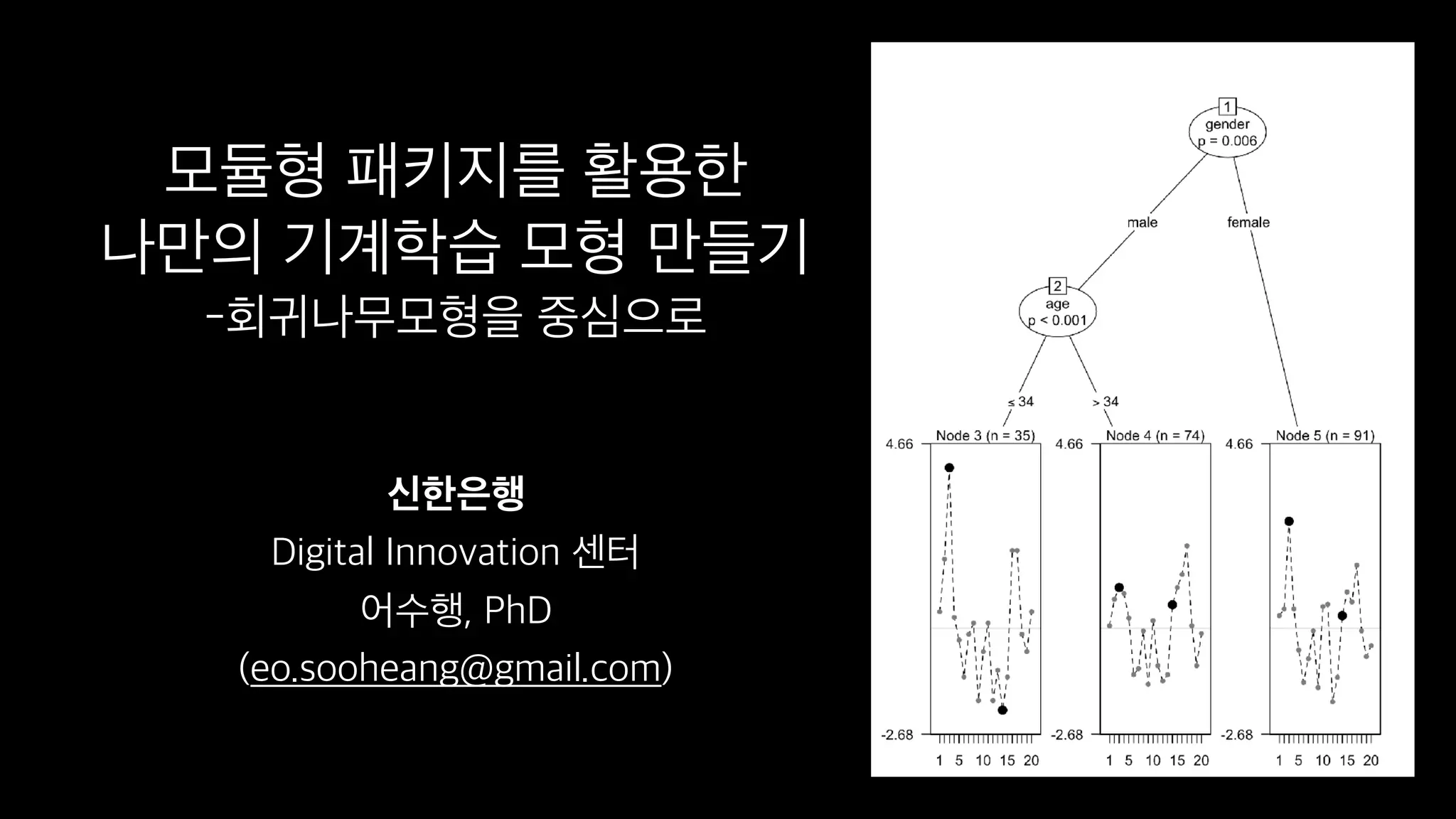
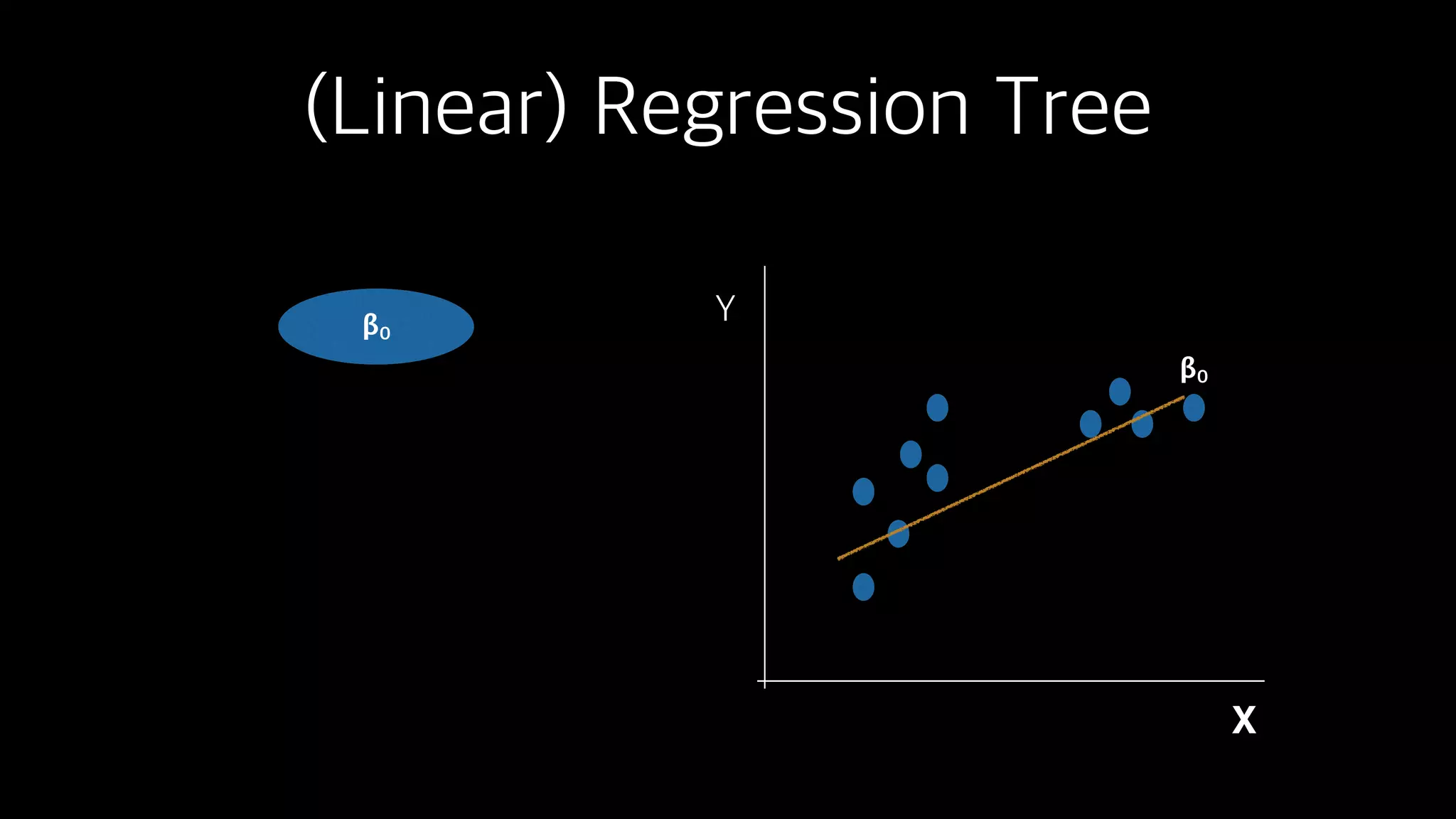
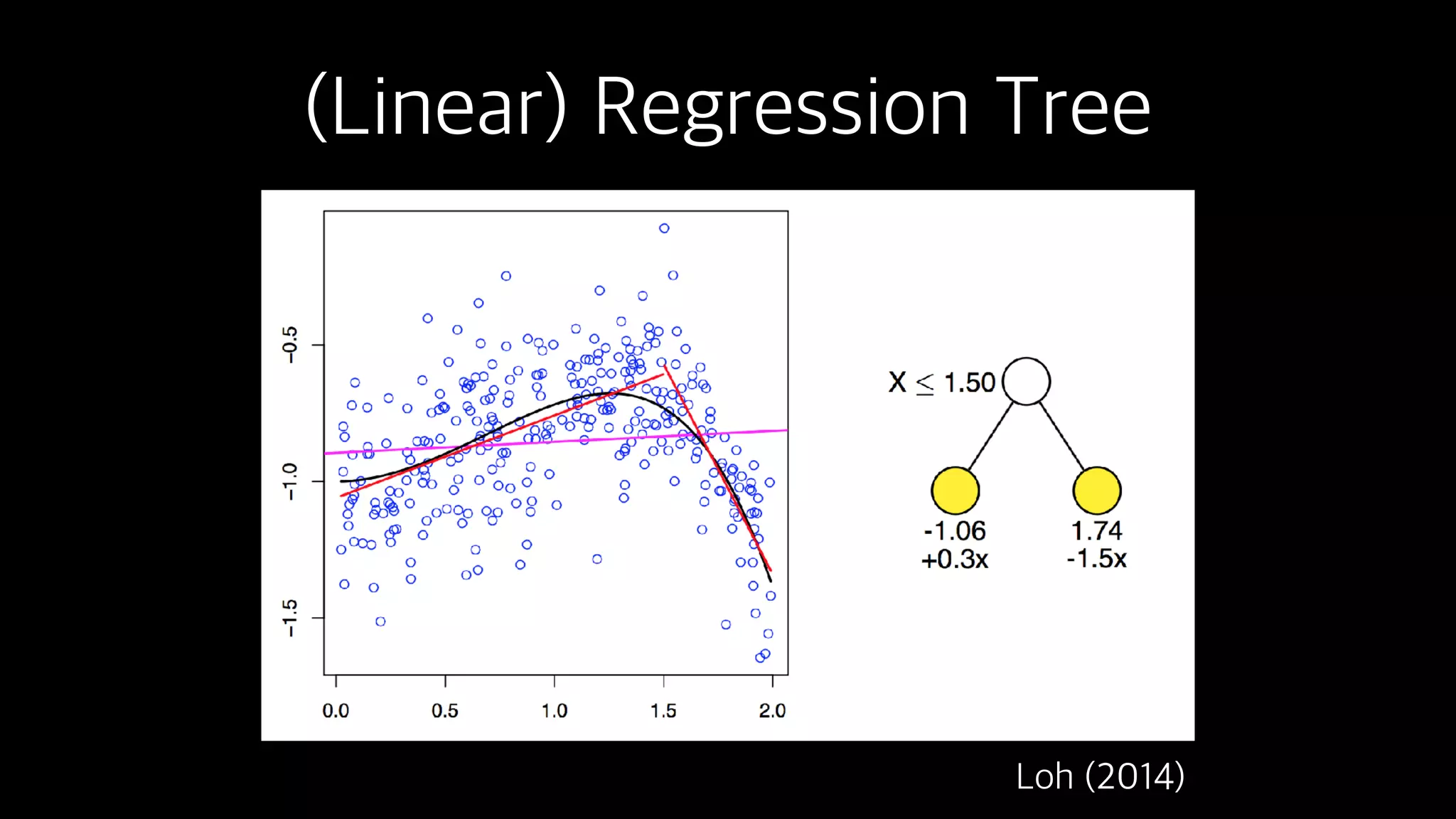
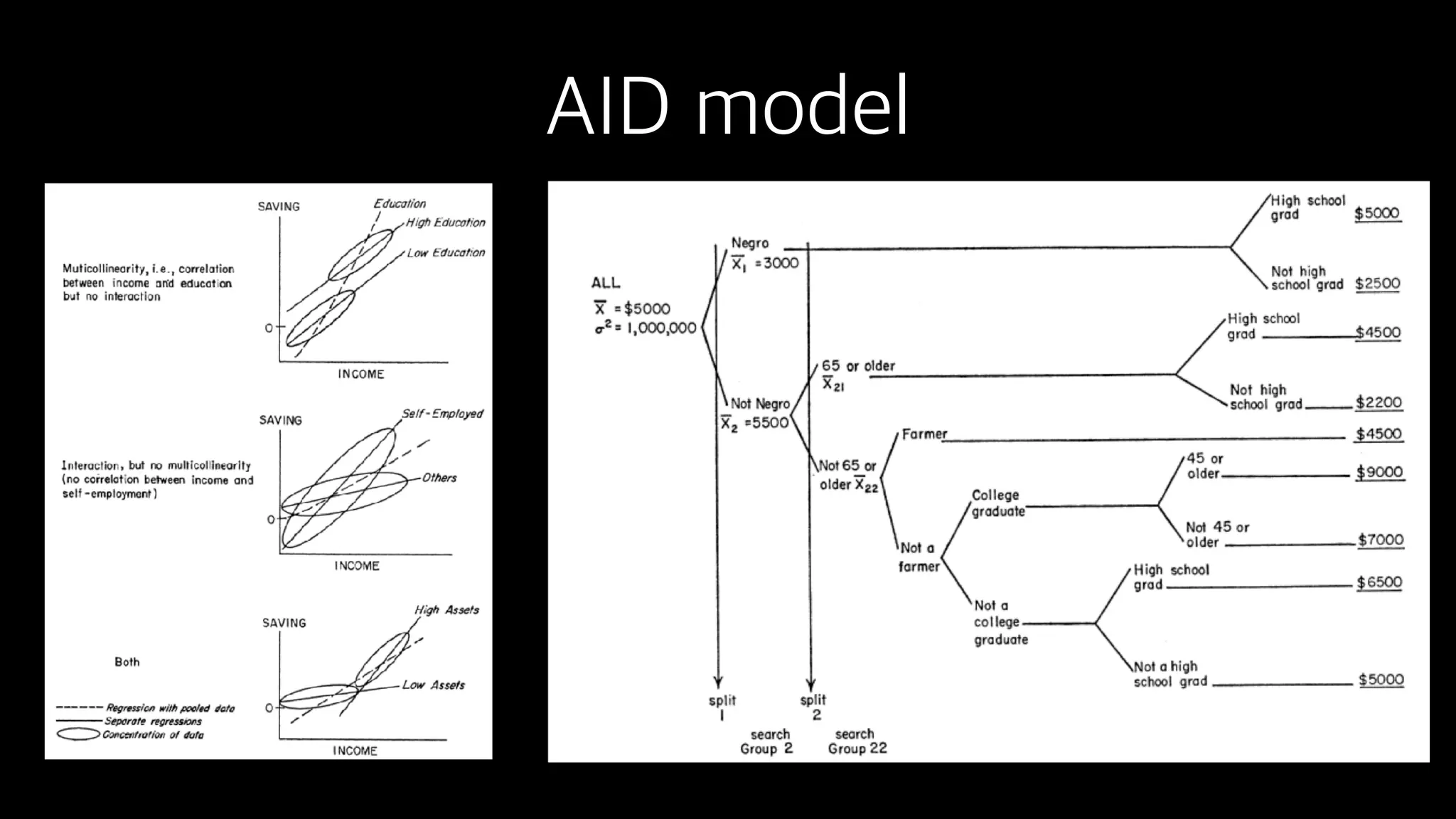
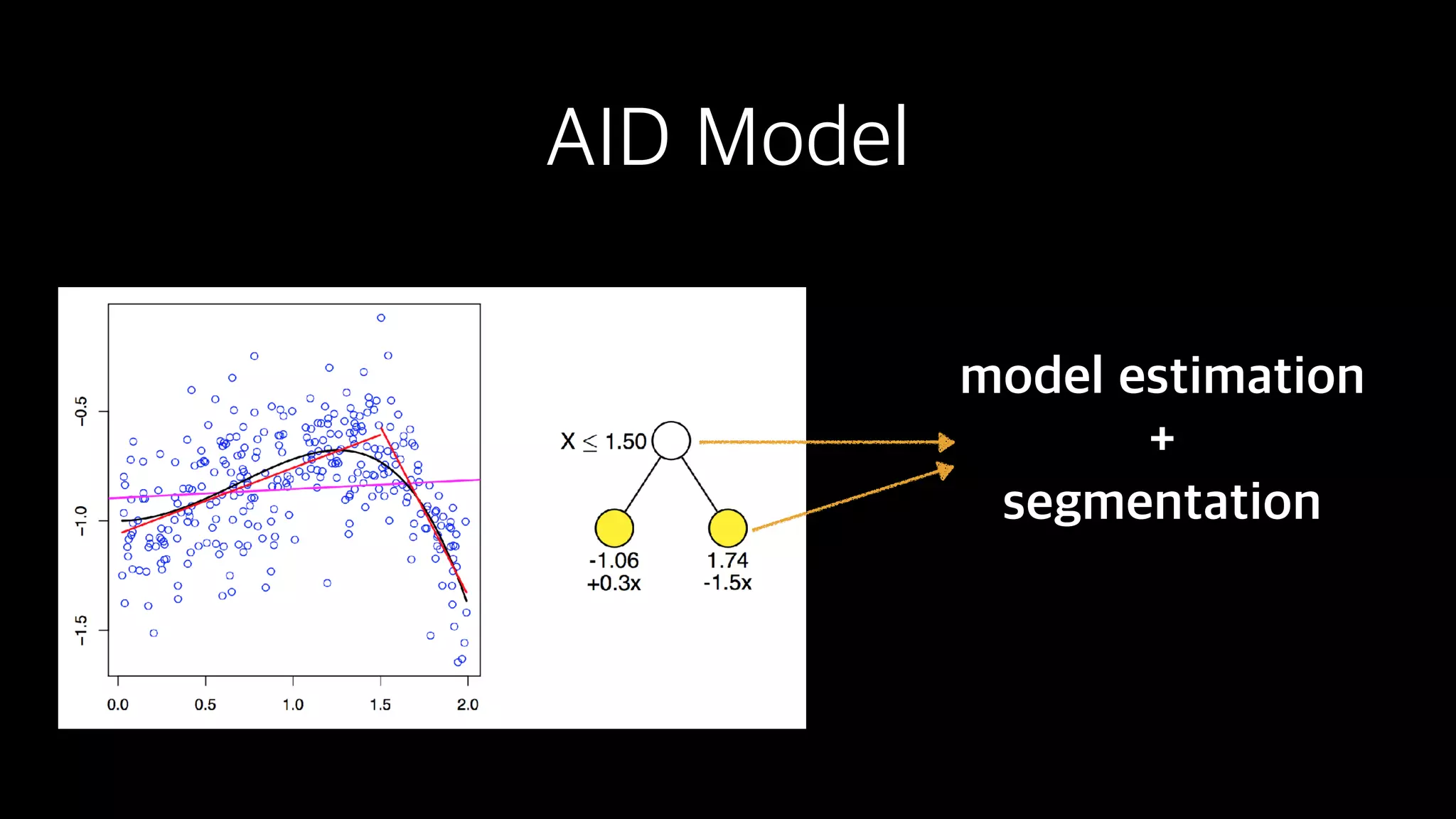
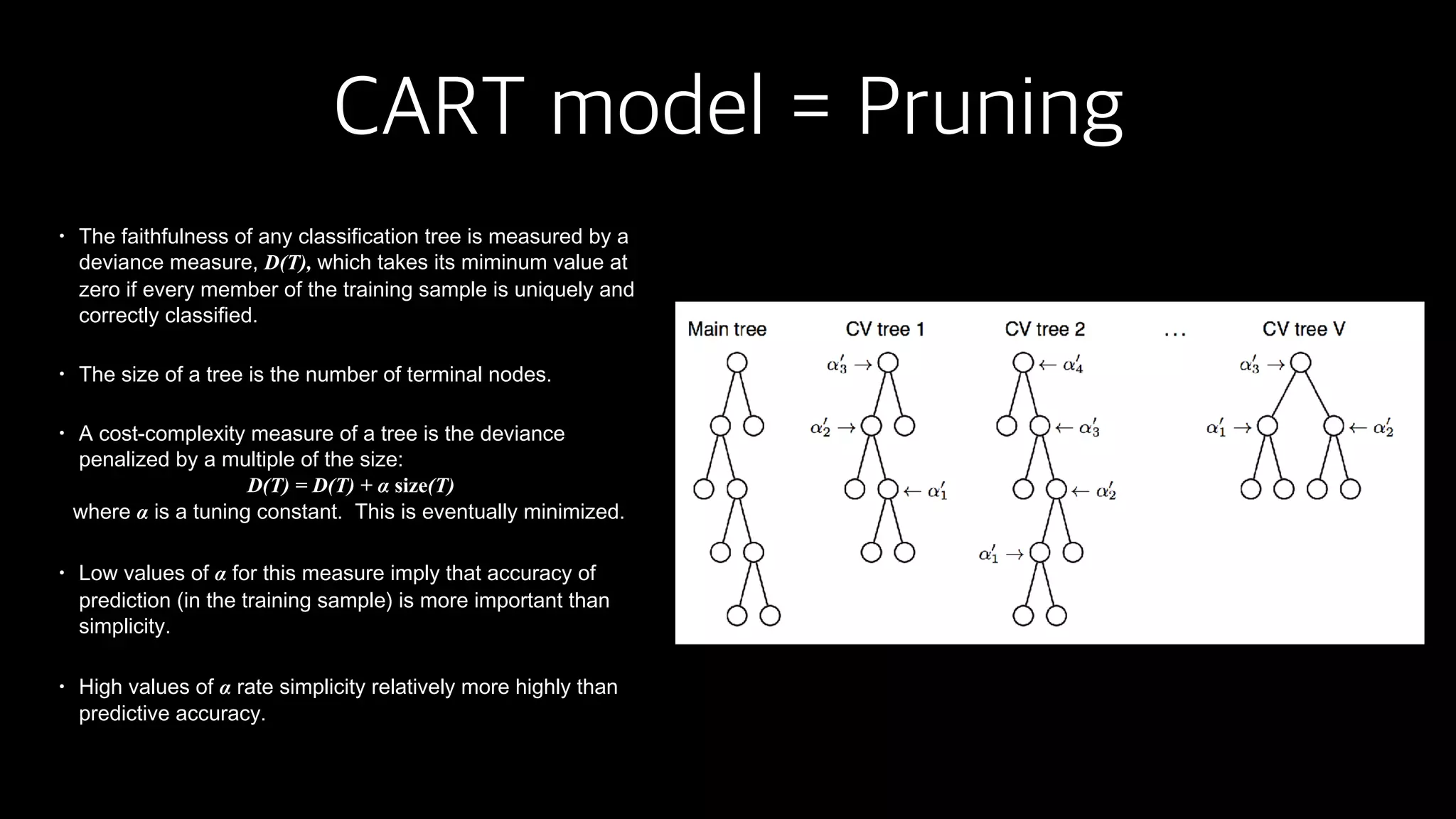
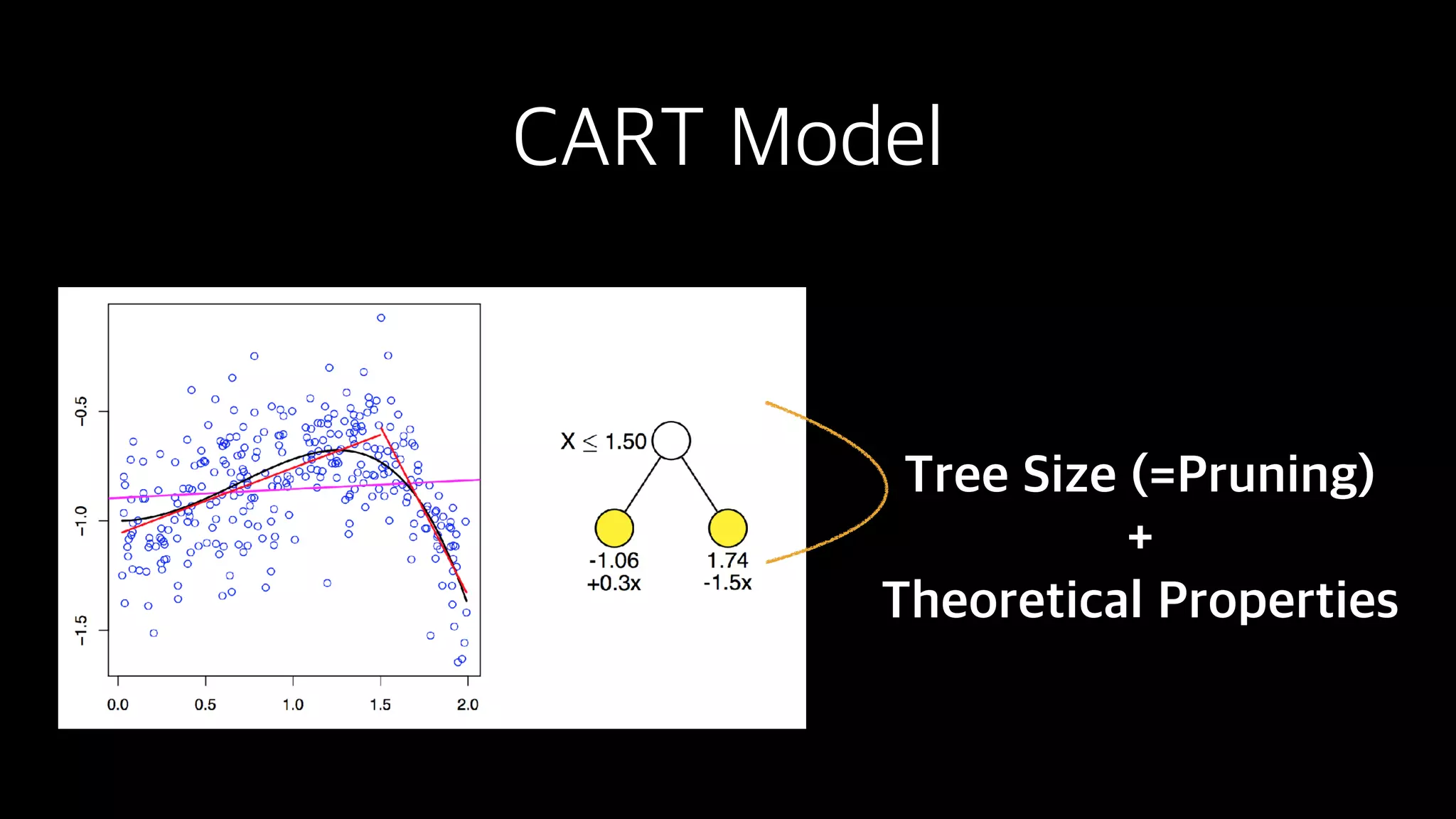
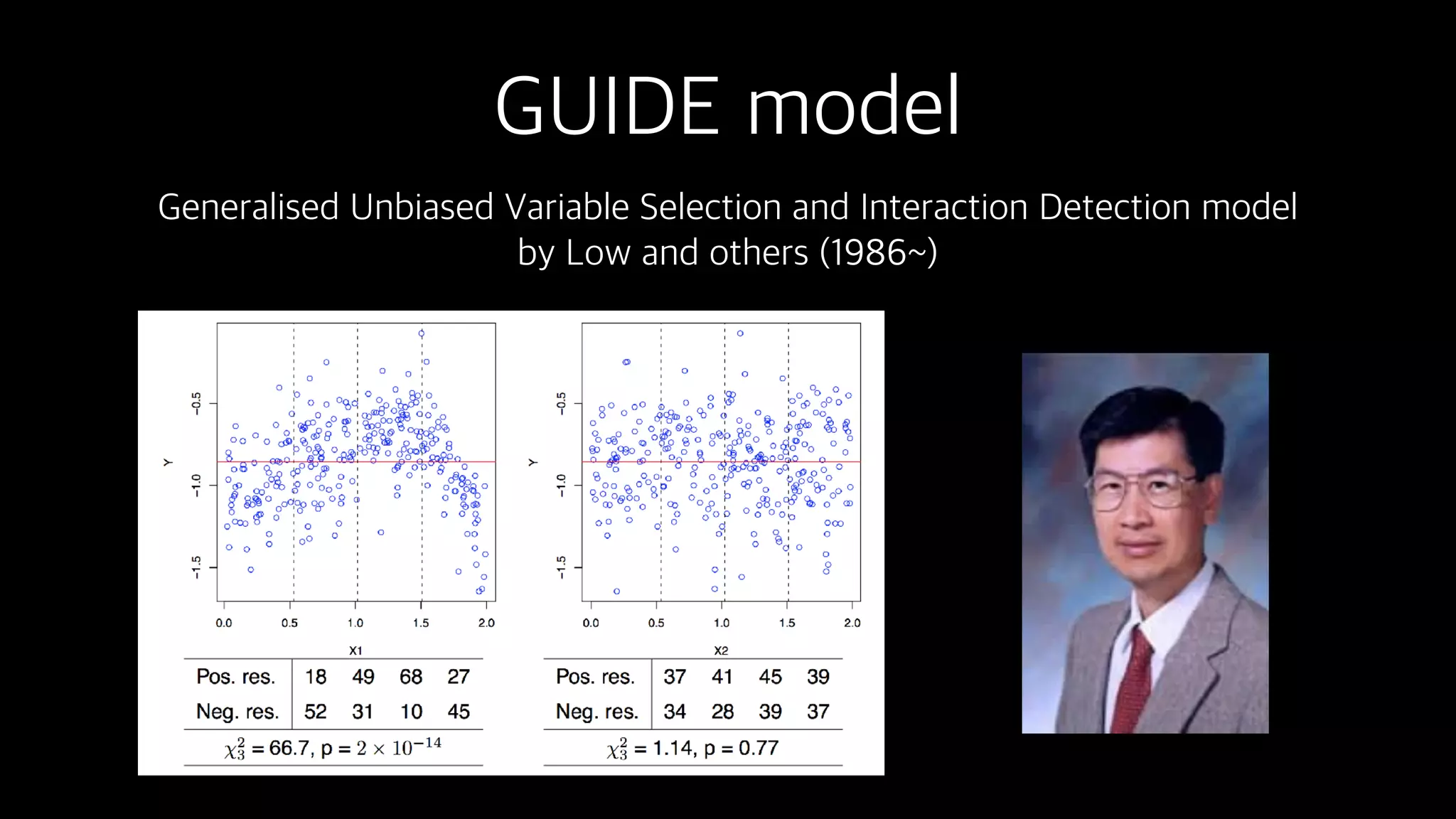
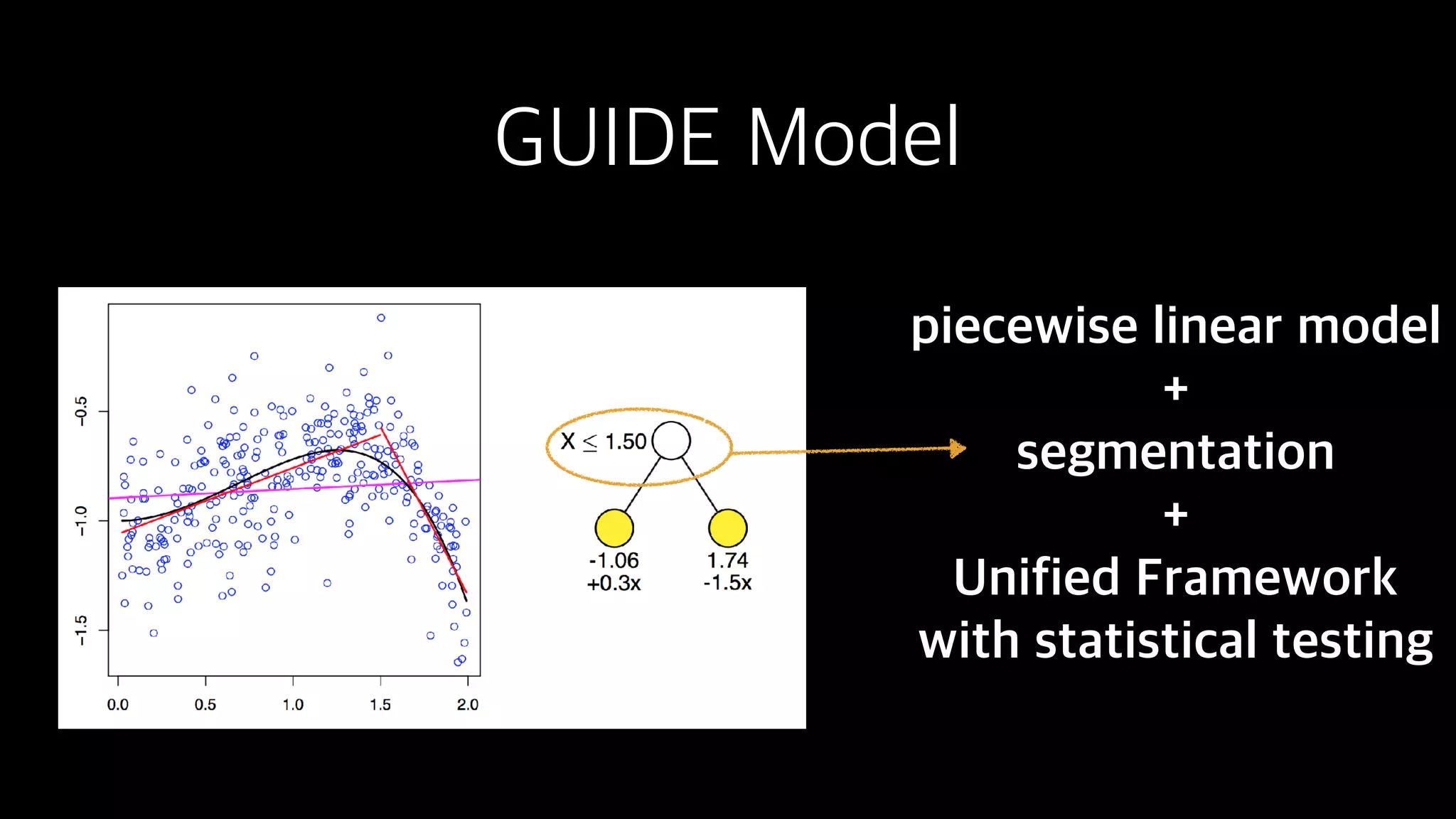
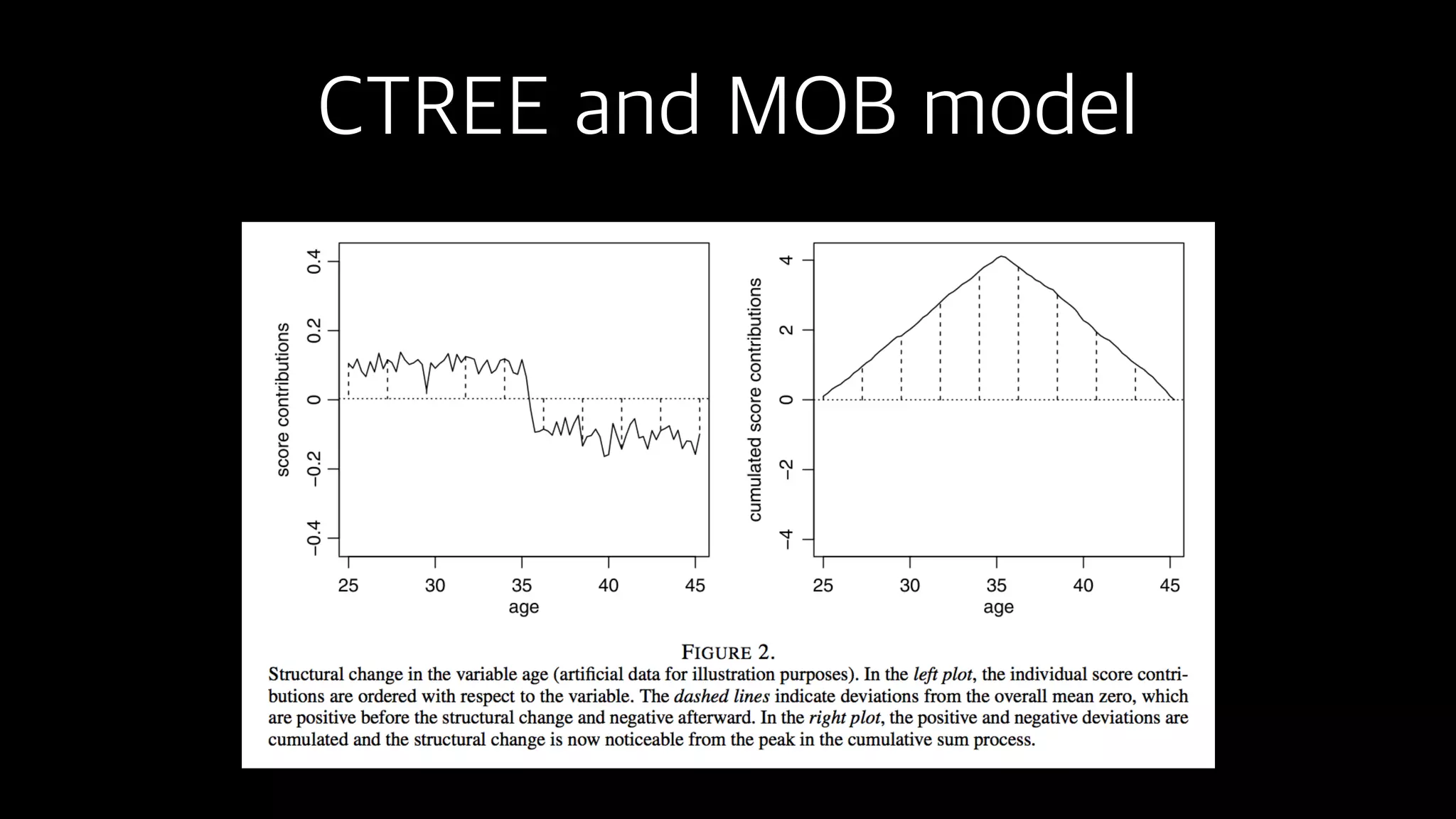
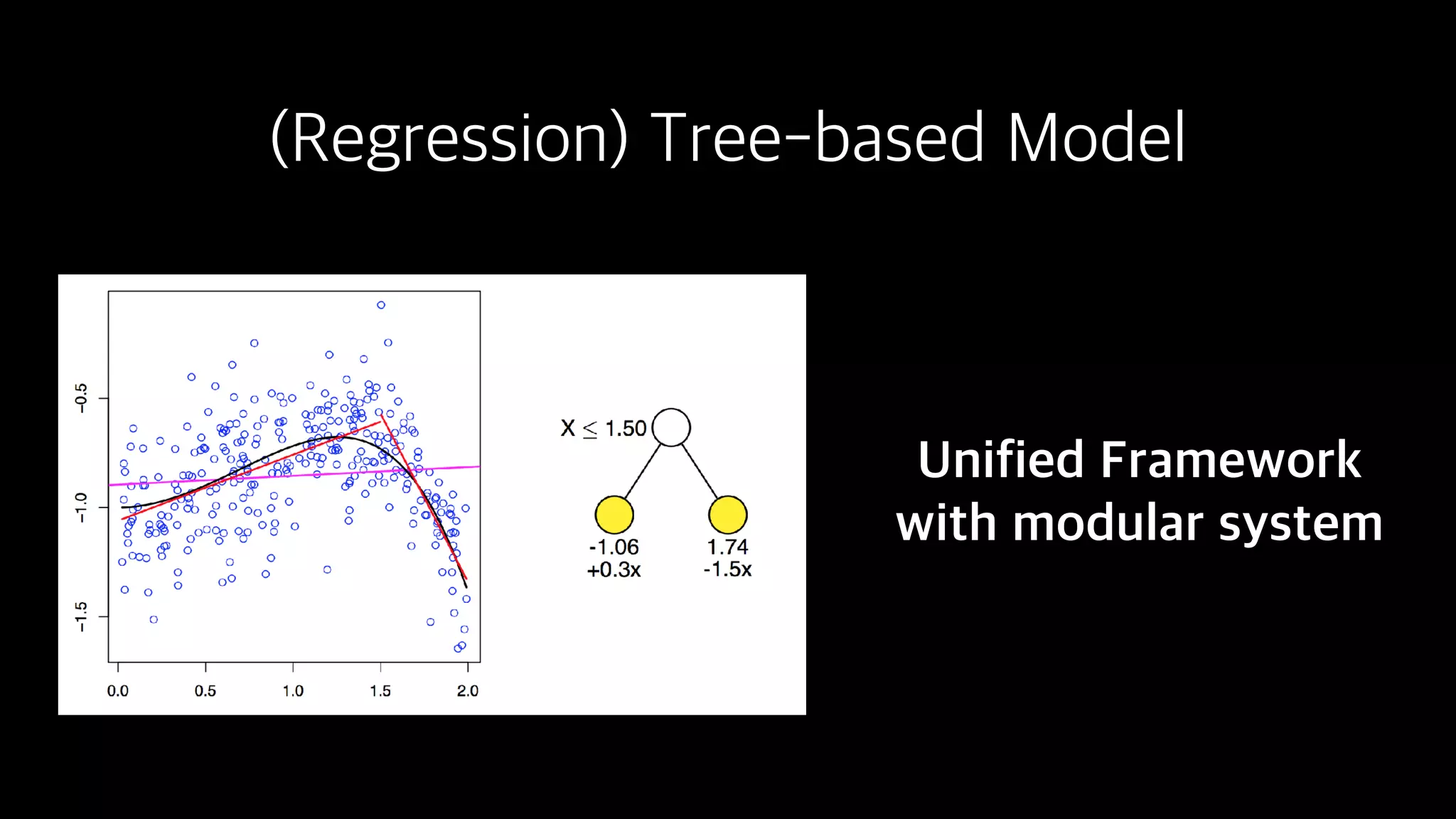
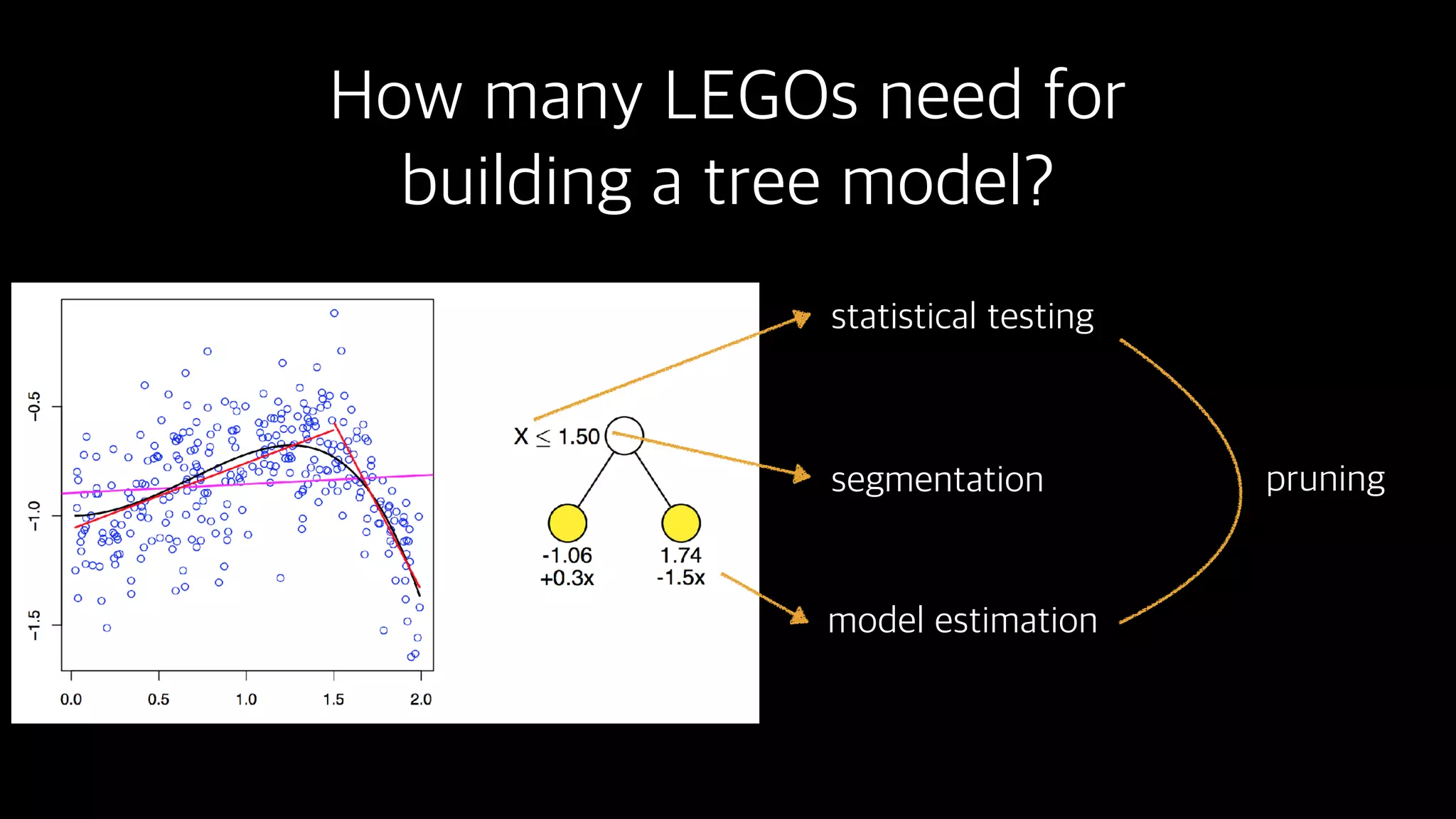
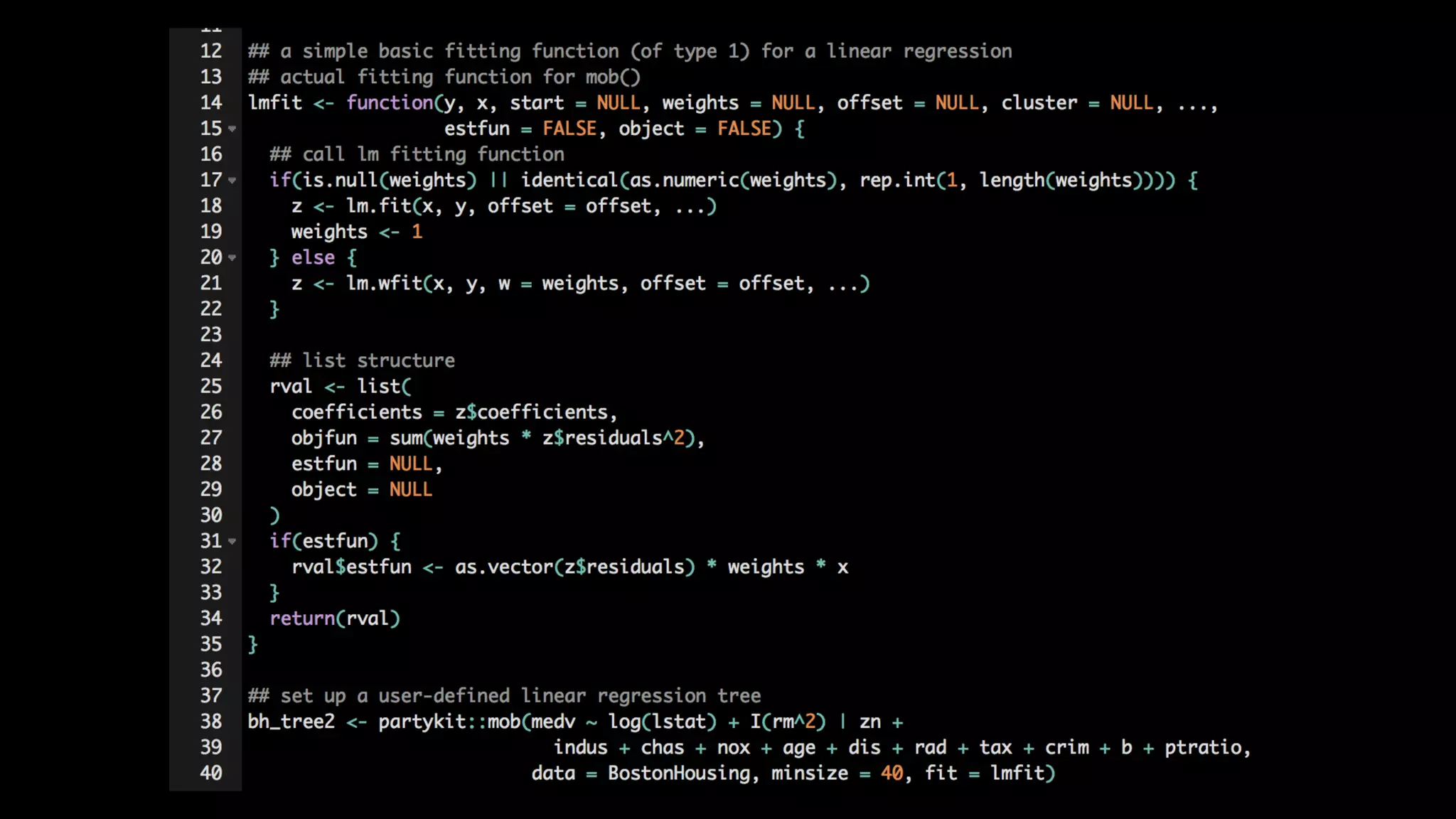
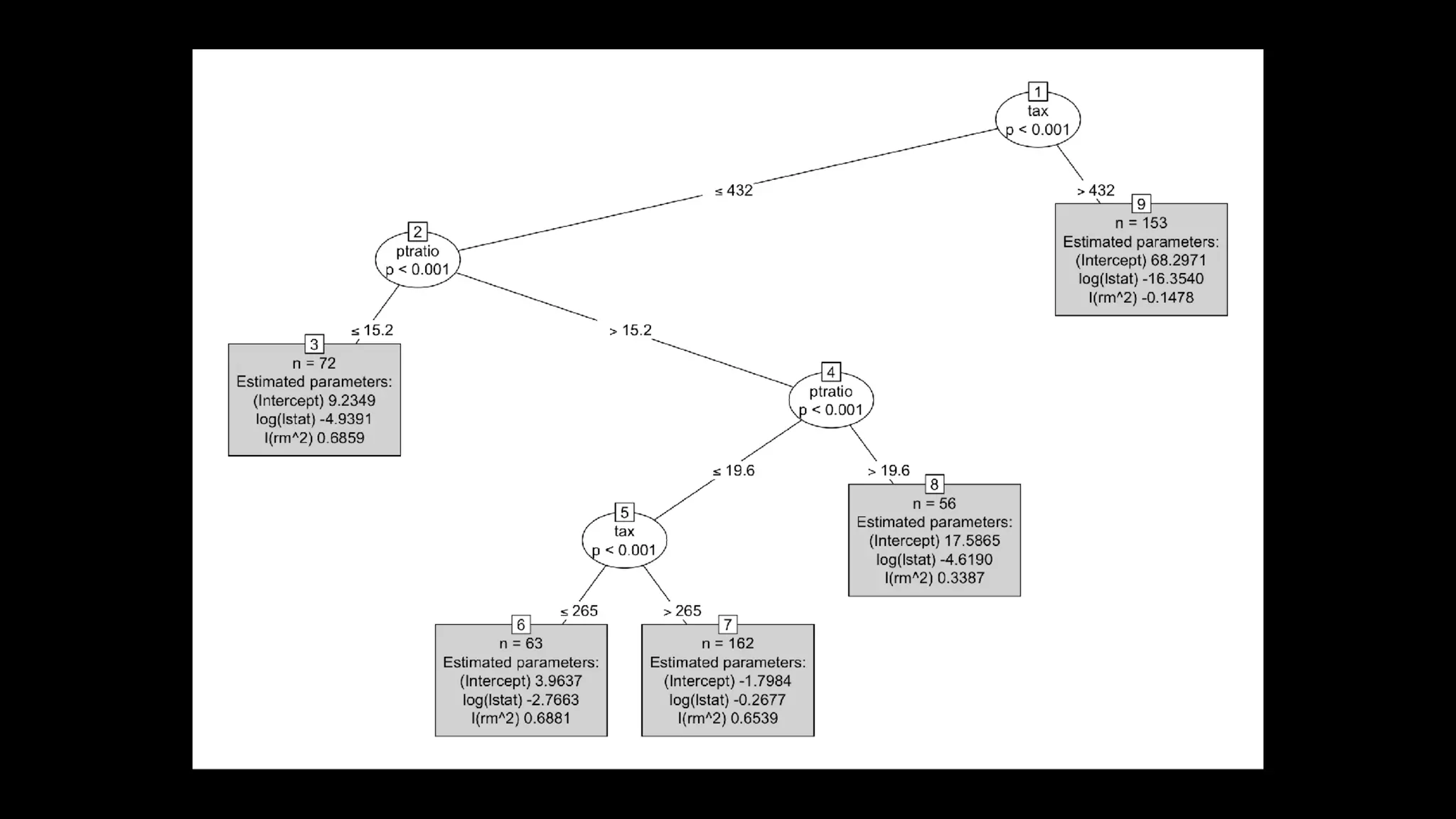
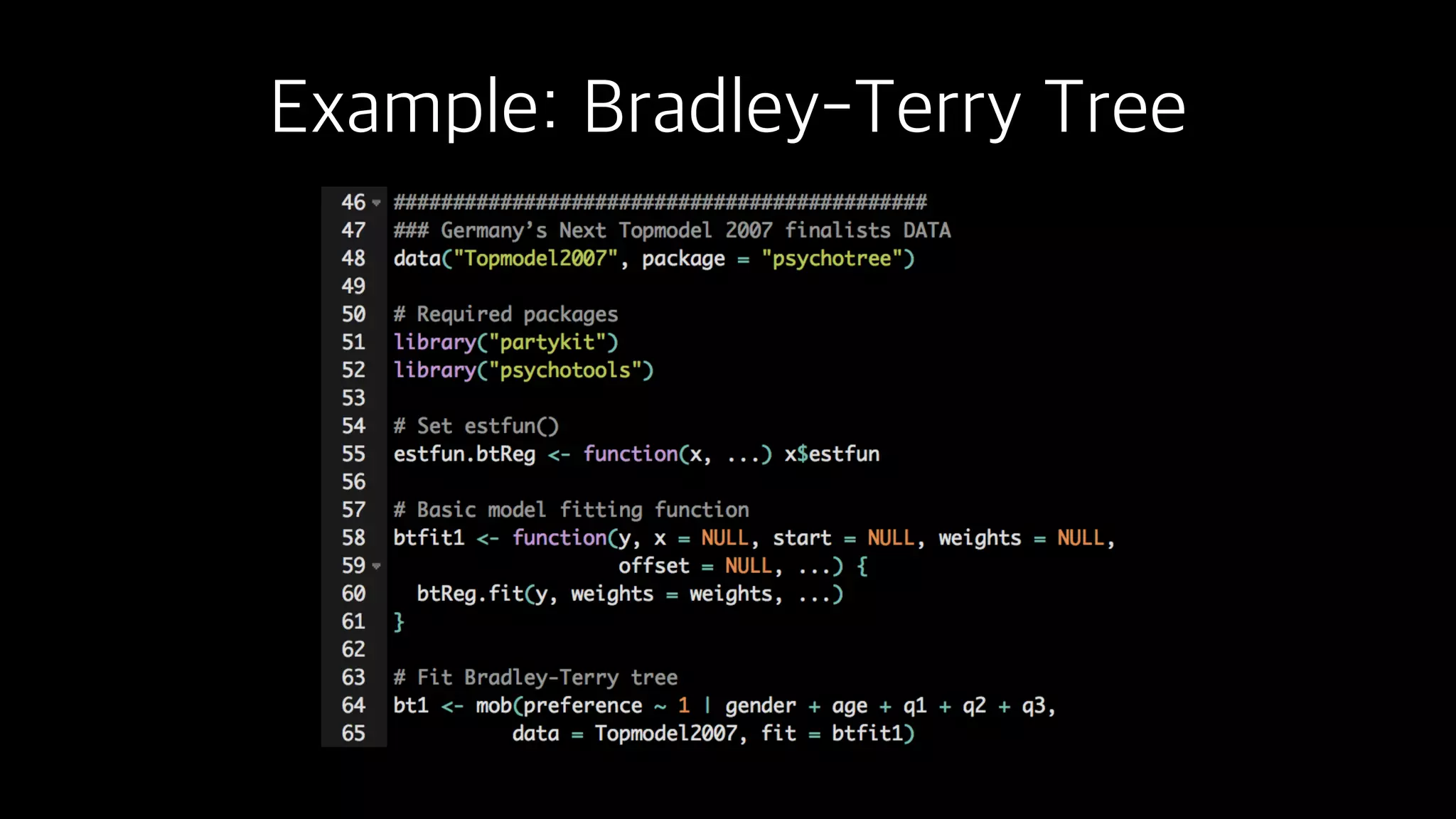
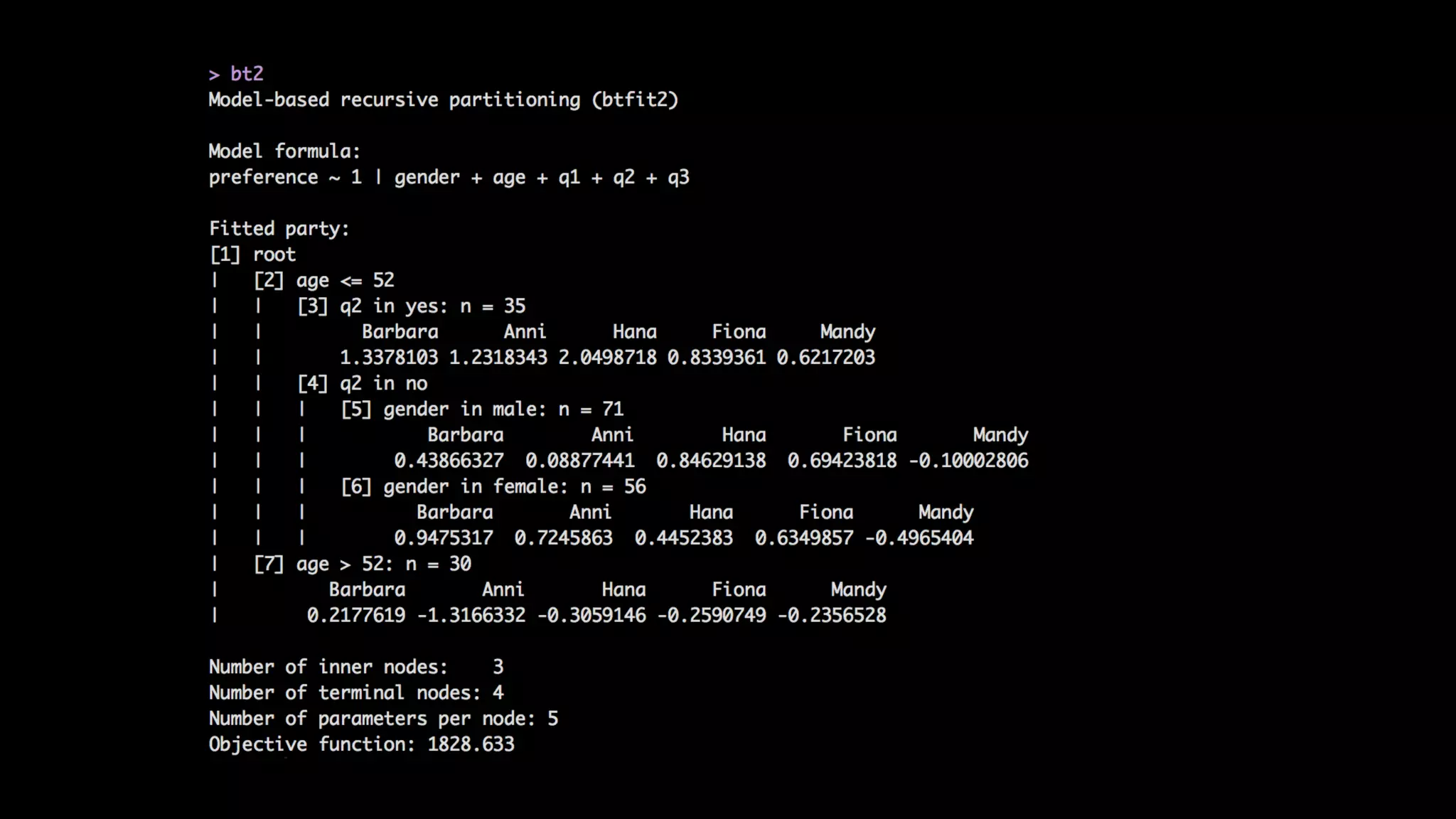
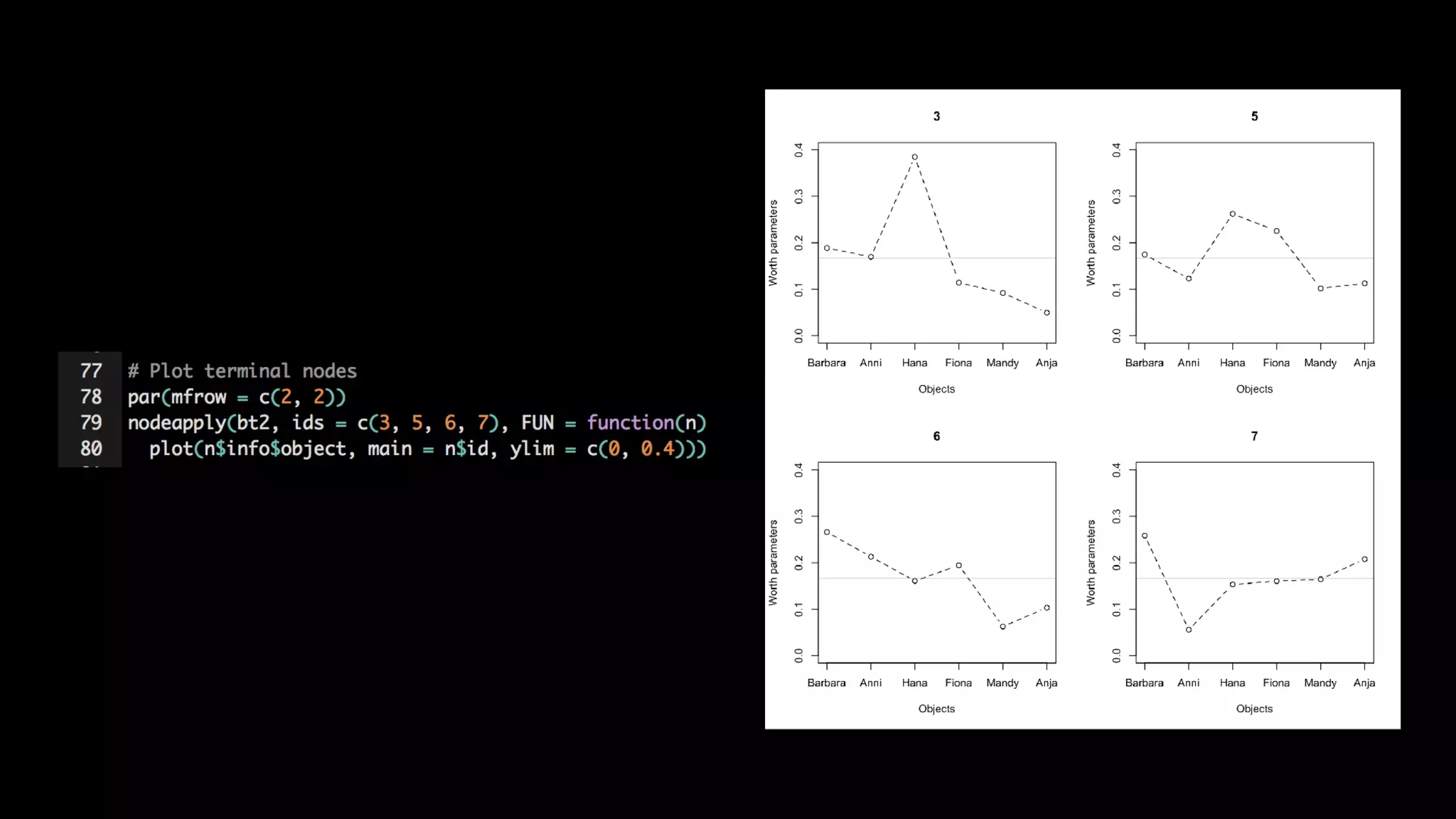
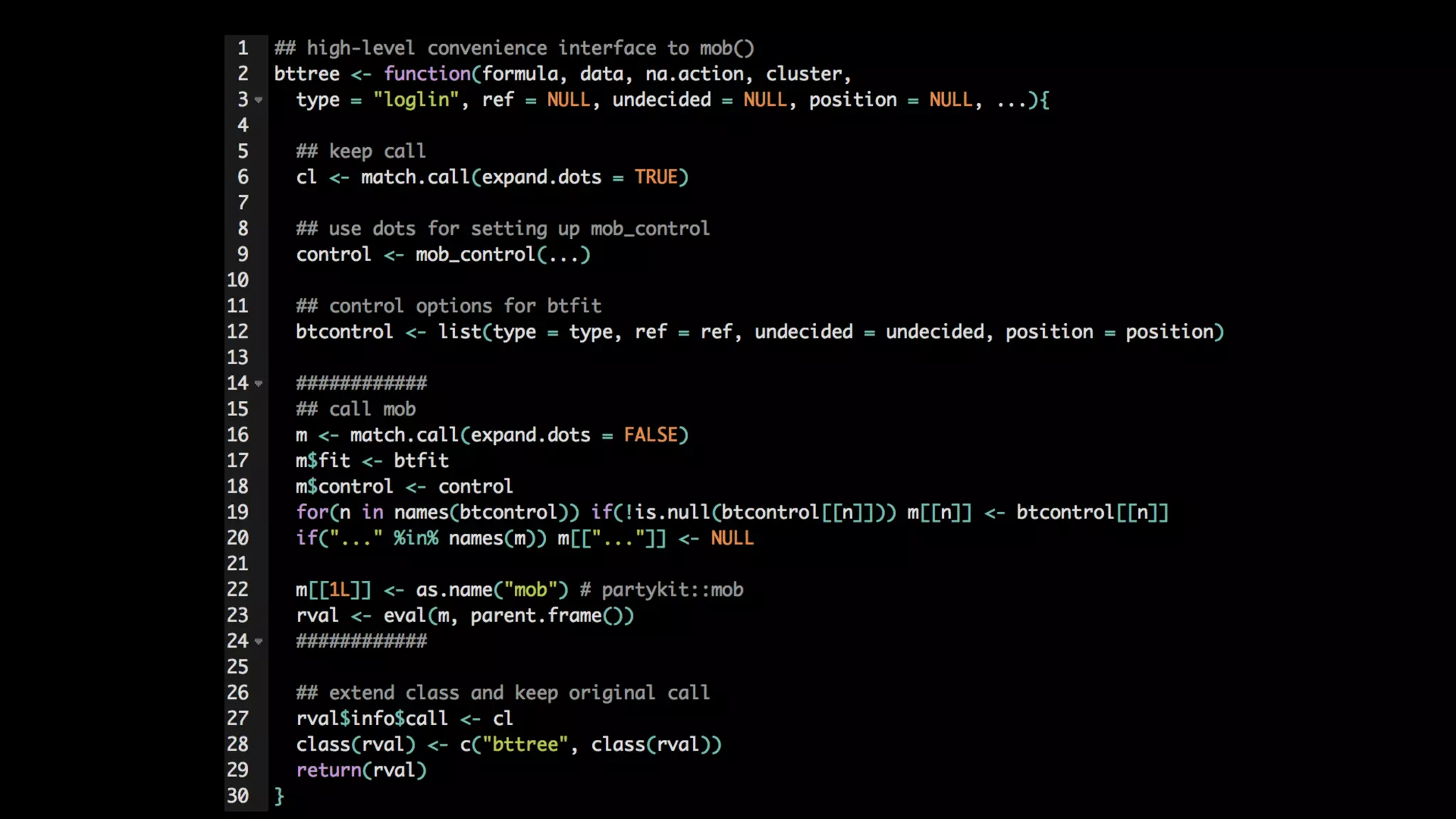
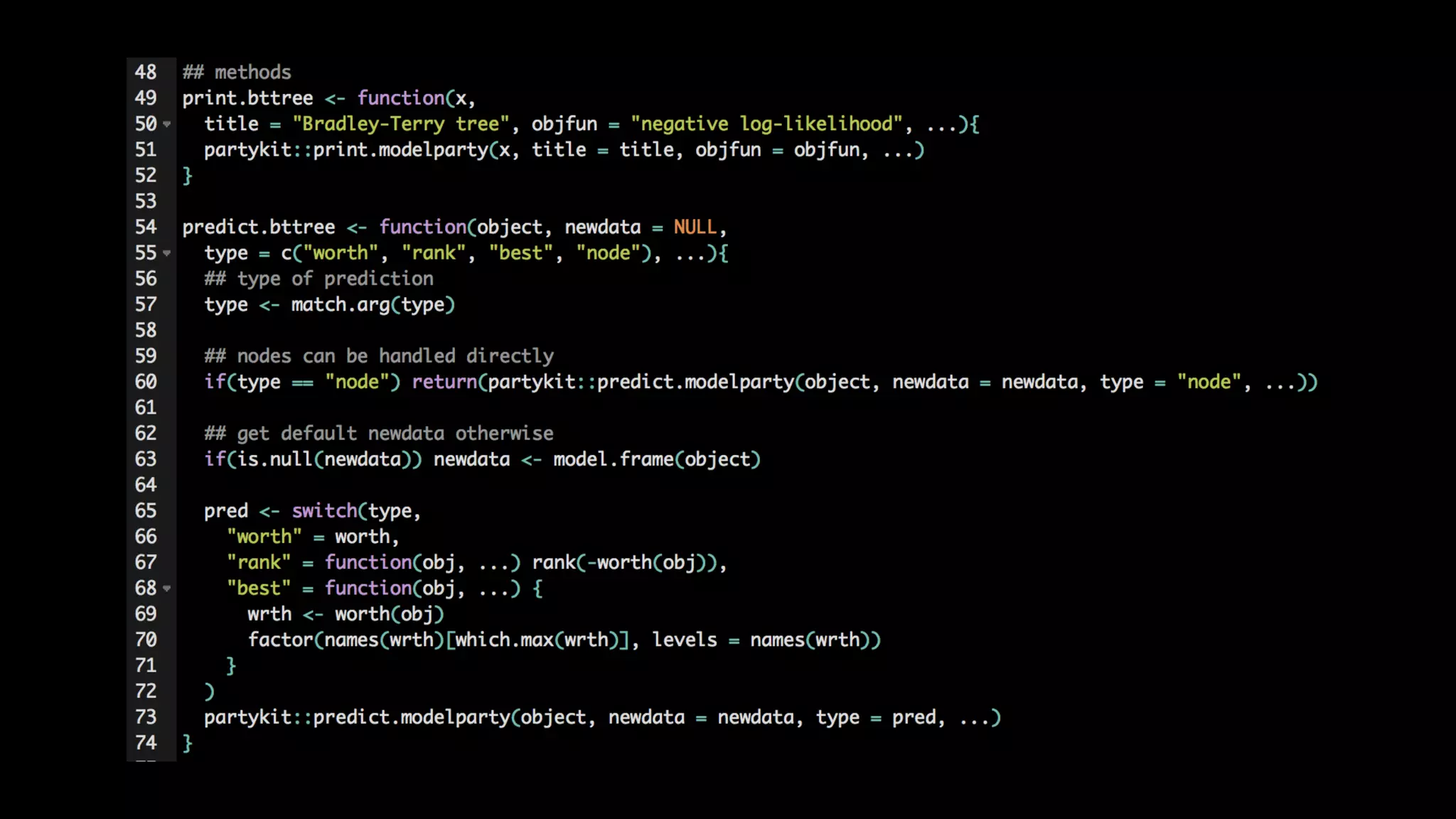
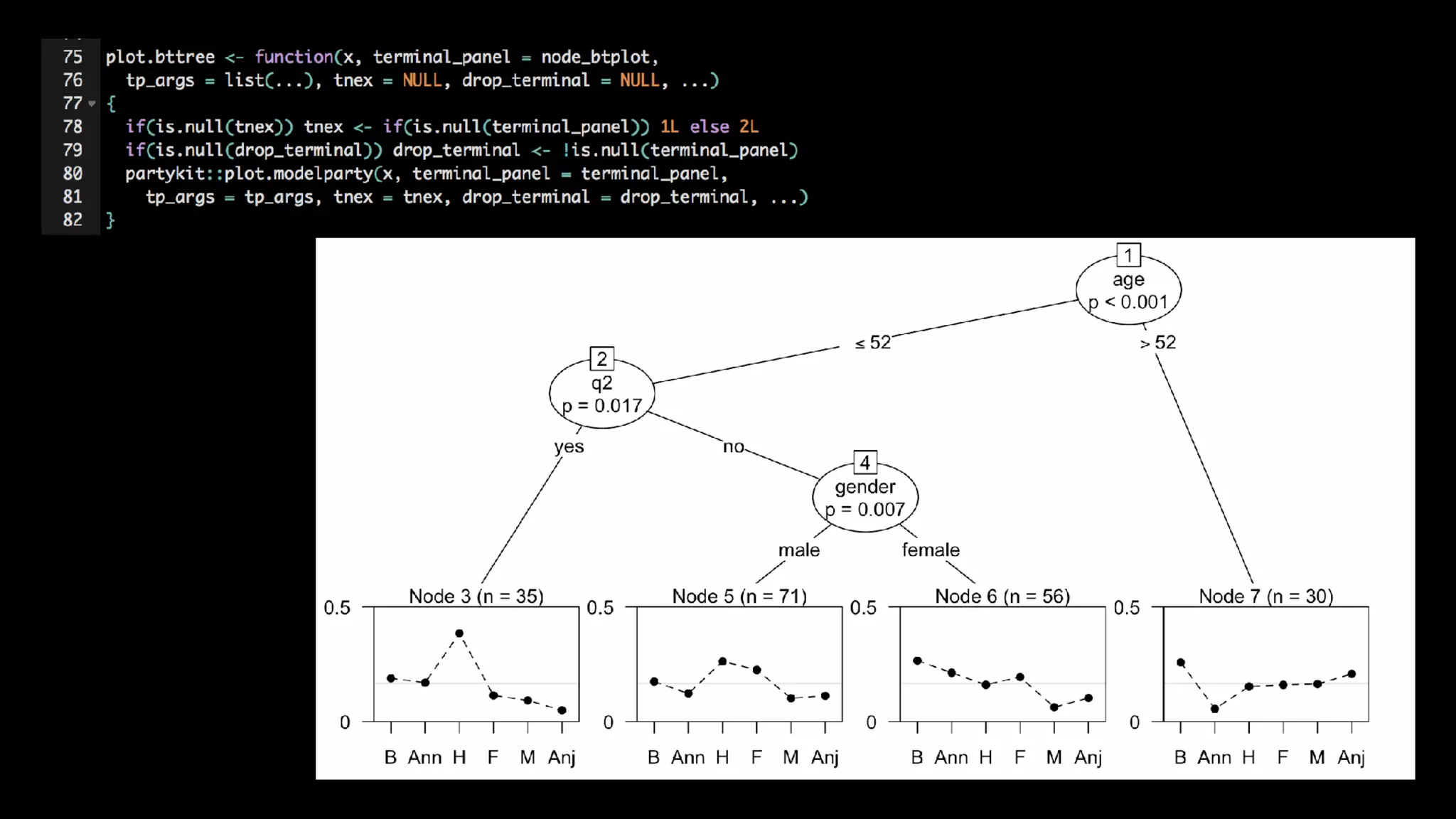
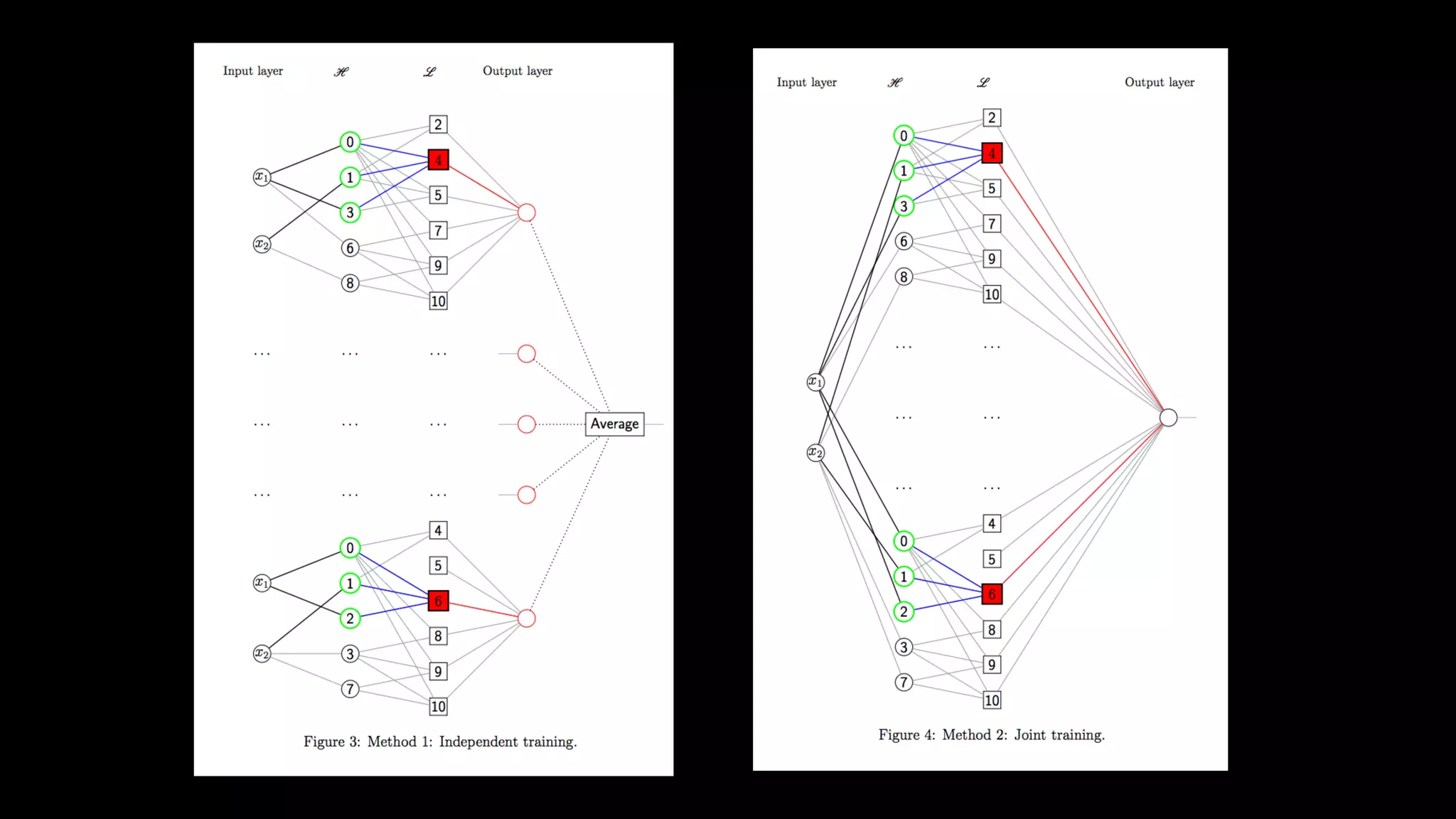
This document discusses the history and implementation of regression tree models. It begins by covering early tree models from the 1960s-1980s like CART and GUIDE. It then discusses more modern unified frameworks using modular packages in R like partykit and mob models. The document provides an example using a Bradley-Terry tree to model preferences from paired comparisons. It concludes by discussing potential extensions to deep learning methods.

1. 모듈형 패키지를 활용한
나만의 기계학습 모형 만들기
-회귀나무모형을 중심으로
신한은행
Digital Innovation 센터
어수행, PhD
(eo.sooheang@gmail.com)

2. Translating statistical ideas into software.
R = Statistical Software

3. 목 차
•모형구현의 시각에서 본 회귀나무모형 역사
•모듈러 패키지를 활용한 회귀나무모형 구현

4. 본 세션은 아래와 같은 분들을 위해 기획되었습니다.
• 대상: 연구자/대학원생
• 연구분야: 사회과학(심리)/의학(병리 혹은 예방)
• 아래 분야에 대한 전문지식이 있으시면 세션이해가 수월하실 듯 합니다.
-> 교과서가 아닌 실무(연구)에서의 통계적 가설검정 경험
-> 1학기 분량의 기계학습 정규과정 수강 경험
-> R(혹은 SAS, Python)에서 tree model을 사용해본 경험

5. (Linear) Regression
£Input Variables: X=(X1, X2, …, Xp) ∈ Rp
£Target Variable: Y ∈ R
£Model: Yi= β0+β1X1i+ β2X2i+…+βp Xpi+εi,
εi~ iid N(0, σ2)
£Parameters for Regression Coefficients:
(β0,β1,β2,…,βp)
Y
X

6. (Linear) Regression
£Input Variables: X=(X1, X2, …, Xp) ∈ Rp
£Target Variable: Y ∈ R
£Model: Yi= β0+β1X1i+ β2X2i+…+βp Xpi+εi,
εi~ iid N(0, σ2)
£Parameters for Regression Coefficients:
(β0,β1,β2,…,βp)
Y
X

7. (Linear) Regression Tree
β0
Y
X
β0

8. (Linear) Regression Tree
Y
Xc
β0
β1 β2
x <= c x > c
β1
β2

9. (Linear) Regression Tree
Loh (2014)

10. Decision Tree
Recursive Partitioning
Tree(-structured) Model
Classification (Regression) Tree

11. (Linear) Regression Tree
• A tree model is a logical model represented as a tree that shows how the value
of a target variable can be predicted by using the values of a set of predictor
(input) variables.
• A tree model recursively partitions the data and sample space to construct the
predictive model.
• Its name derives from the practice of displaying the partitions as a decision tree,
from which the roles of the predictor variables may be inferred.
• The idea was first implemented by Morgan and Sonquist in 1963. It is called the
AID (Automatic Interaction Detection) algorithm.

12. AID model
Automatic Interaction Detection (AID) model by Morgan and Sonquist (1963; JASA)
http://home.isr.umich.edu/education/fellowships-awards/james-morgan-fund/

13. AID model

14. Code name ‘SEARCH’
Automatic Interaction Detector Program
(Sonquist and Morgan, 1964)
Enhanced version of the AID program
(Sonquist et al., 1974)

15. AID Model
model estimation
+
segmentation

16. CART model
Classification and Regression Tree (CART) model by BFOS (1976~)
Leo Breiman Jerome Friedman Richard Olshen Charles Stone

17. CART model
Stone (1977). Consistent Nonparametric Regression(with discussion), The Annals of Statistics, 5, 590-625

18. CART model = Pruning
• The faithfulness of any classification tree is measured by a
deviance measure, D(T), which takes its miminum value at
zero if every member of the training sample is uniquely and
correctly classified.
• The size of a tree is the number of terminal nodes.
• A cost-complexity measure of a tree is the deviance
penalized by a multiple of the size:
D(T) = D(T) + α size(T)
where α is a tuning constant. This is eventually minimized.
• Low values of α for this measure imply that accuracy of
prediction (in the training sample) is more important than
simplicity.
• High values of α rate simplicity relatively more highly than
predictive accuracy.

19. Implementation of CART model
tree package rpart package

20. Implementation of CART model
tree package rpart package

21. Implementation of CART model
• In R there is a native tree library that V&R have some reservations about. It is useful,
though.
•rpart is a library written by Beth Atkinson and Terry Therneau of the Mayo Clinic,
Rochester, NY. It is much closer to the spirit of the original CART algorithm of Breiman,
et al. It is now supplied with both S-PLUS and R.
• In R, there is a tree library that is an S-PLUS look-alike, but we think better in some
respects.
•rpart is the more flexible and allows various splitting criteria and different model bases
(survival trees, for example).
•rpart is probably the better package, but tree is acceptable and some things such as
cross-validation are easier with tree.
• In this discussion we (nevertheless) largely use tree!

22. Implementation of CART model
https://cran.r-project.org/package=rpart

23. CART Model
Tree Size (=Pruning)
+
Theoretical Properties

24. GUIDE model
Generalised Unbiased Variable Selection and Interaction Detection model
by Low and others (1986~)

25. Implementation of GUIDE model
IBM SPSS
GUIDE CORE
(Fortran95)
GUIDE Interface

26. GUIDE Model
piecewise linear model
+
segmentation
+
Unified Framework
with statistical testing

27. CTREE and MOB model
Model-based Recursive Partitioning by Hothorn and Zeileis (2004~)

28. CTREE and MOB model
Models: Estimation of parametric models with observations yi (and
regressors xi), parameter vector θ, and additive objective function Ψ.
Recursive partitioning:
1 Fit the model in the current subsample.
2 Assess the stability of θ across each partitioning variable zj.
3 Split sample along the zj∗ with strongest association: Choose breakpoint
with highest improvement of the model fit.
4 Repeat steps 1–3 recursively in the subsamples until some stopping
criterion is met.
ˆ✓ = argmin✓
P
i
0
(yi, xi, ˆ✓)

29. CTREE and MOB model

30. Implementation of MOB model

31. (Regression) Tree-based Model
Unified Framework
with modular system

32. 정리 (tree model의 관점)
• 1세대 - Michigan (1964 ~ 199x)
piecewise constant model with exhaustive (heuristic) search
• 2세대 - Berkely & Stanford (1972 ~ 200x)
Unified tree framework with exhastive search
• 2.5세대 - Wisconsin & ISI (1986 ~ 201x)
Unified tree framework with statistical testing
• 3세대 - LMU & Upenn & UNC (2005 ~ 201x)
Unified tree framework with piecewise model-based model
+ extensions (Domain / Bayesian Approaches / Tree-structured Objects)
순도 100% 개인적 생각

33. 정리 (구현 관점)
The CRAN task view on “Machine Learning” at http://CRAN.R-project.org/
view=MachineLearning lists numerous packages for tree-based modeling and
recursive partitioning, including
– rpart (CART),
– tree (CART),
– mvpart (multivariate CART),
– RWeka (J4.8, M5’, LMT),
– party (CTree, MOB),
– and many more (C50, quint, stima, . . . ).
Related: Packages for tree-based ensemble methods such as random forests or
boosting, e.g., randomForest, gbm, mboost, etc.

34. 모듈형 패키지를 활용한
나만의 회귀나무모형 만들기

35. How many LEGOs need for
building a tree model?
segmentation
statistical testing
model estimation
pruning

36. 1 Fit a model to the y or y and x variables using the observations in the
current node
2 Assess the stability of the model parameters with respect to each of the
partitioning variables z1, ..., zl. If there is some overall instability, choose
the variable z associated with the smallest p value for partitioning,
otherwise stop.
3 Search for the locally optimal split in z by minimizing the objective
function of the model. Typically, this will be something like deviance or
the negative logLik.
4 Refit the model in both kid subsamples and repeat from step 2.
How many LEGOs need for
building a tree model?
http://partykit.r-forge.r-project.org/partykit/outreach/

37. modular R package - partykit
http://partykit.r-forge.r-project.org/partykit/outreach/

38. Example: Linear Model Tree

39. Example: Linear Model Tree

41. Example: Linear Model Tree

42. Example: Linear Model Tree

44. Implementation: Models
Input: Basic interface.
fit(y, x = NULL, start = NULL, weights = NULL,
offset = NULL, ...)
y, x, weights, offset are (the subset of) the preprocessed data.
Starting values and further fitting arguments are in start and ....
Output: Fitted model object of class with suitable methods.
coef(): Estimated parameters hat_{theta}
logLik(): Maximized log-likelihood function .
estfun(): Empirical estimating functions Ψ0
http://partykit.r-forge.r-project.org/partykit/outreach/

45. Implementation: Models
Input: Extended interface.
fit(y, x = NULL, start = NULL, weights = NULL,
offset = NULL, ..., estfun = FALSE, object = FALSE)
Output: List object
coefficients: Estimated parameters
objfun: Minimized objective function
estfun: Empirical estimating functions
object: A model object for which further methods could be
available (e.g., predict(), or fitted(), etc.).
Internally: Extended interface constructed from basic interface if
supplied. Efficiency can be gained through extended approach.
ˆ✓ P
i (yi, xi, ˆ✓)
0
(yi, xi, ˆ✓)
http://partykit.r-forge.r-project.org/partykit/outreach/

46. Implementation: Framework
Class: ‘modelparty’ inheriting from ‘party’.
Main addition: Data handling for regressor and partitioning variables.
The Formula package is used for two-part formulas, e.g.,
y ~ x1 + x2 | z1 + z2 + z3.
The corresponding terms are stored for the combined model and
only for the partitioning variables.
Additional information: In info slots of ‘party’ and ‘partynode’.
call, formula, Formula, terms (partitioning variables only),
fit, control, dots, nreg.
coefficients, objfun, object, nobs, p.value, test.
Reusability: Could in principle be used for other model trees as well
(inferred by other algorithms than MOB).
http://partykit.r-forge.r-project.org/partykit/outreach/

47. Example: Bradley-Terry Tree
http://partykit.r-forge.r-project.org/partykit/outreach/

48. Example: Bradley-Terry Tree
• Task: Preference scaling of attractiveness.
• Data: Paired comparisons of attractiveness.
Germany’s Next Topmodel 2007 finalists:
Barbara, Anni, Hana,Fiona, Mandy, Anja.
Survey with 192 respondents at Universit t T bingen.
Available covariates: Gender, age, familiarty with the TV show.
Familiarity assessed by yes/no questions:
(1) Do you recognize the women?/Do you know the show?
(2) Did you watch it regularly?
(3) Did you watch the final show?/Do you know who won?
http://partykit.r-forge.r-project.org/partykit/outreach/

49. Example: Bradley-Terry Tree
Model: Bradley-Terry (or Bradley-Terry-Luce) model.
Standard model for paired comparisons in social sciences.
Parametrizes probability for preferring object i over j in terms of
corresponding “ability” or “worth” parameters
Implementation: bttree() in psychotree (Strobl et al. 2011).
Here: Use mob() directly to build model from scratch using
btReg.fit() from psychotools
⇡ij
✓i
⇡ij = ✓i
✓i+✓j
http://partykit.r-forge.r-project.org/partykit/outreach/

50. Example: Bradley-Terry Tree

51. Example: Bradley-Terry Tree

54. bttree() in psychotree

55. bttree() in psychotree

59. 적용

60. Case 1. random effects tree model
Eo and Cho (2014)

61. Case 2. latent variable tree model
Lee et al. (2012); Eo et al. (2014); Eo (2015);

62. Case 3. multiway splits tree model
Eo et al. (2014)Kim and Loh (1998)

63. Case 4. Industry (FDS)

64. Case 5. Industry (Quantile Tree)

65. 마무리

66. Extensions to Deep Learning

68. Summary
R에서
tree-structured model을 쓰지 않는다면
앙꼬없는 찐빵을 먹는것과 같다

69. 매일 밤 졸업을 위해 고민하는 대학원생들에게 본 세션을 바칩니다.
http://www.phdcomics.com/

70. Some review papers
• Loh, W.-Y. (2014). Fifty years of classification and regression trees (with discussion). International Statistical Review, vol,
pages.
• Loh, W.-Y. (2008). Regression by parts: Fitting visually interpretable models with GUIDE. In Handbook of Data Visualization, C.Chen,
W.H rdle, and A.Unwin, Eds. Springer, pp.447-469.
• Loh, W.-Y. (2008). Classification and regression tree methods. In Encyclopedia of Statistics in Quality and Reliability, F.Ruggeri,
R.Kenett, and F.W. Faltin, Eds. Wiley, Chichester, UK, pp.315-323.
• Loh, W.-Y. (2010). Tree-structured classifiers. Wiley Interdisciplinary Reviews: Computational Statistics, 2, 364-369.
• Loh, W.-Y. (2011). Classification and regression trees. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 14-23.
• Merkle, E.C. and Shaffer, V.A. (2011). Binary recursive partitioning: Background, methods, and application to psychology, British
Journal of Mathematical and Statistical Psychology, 64, 161–181.
• Morgan, J. N. and Sonquist, J. A. (1963). Problems in the analysis of survey data, and a proposal. J. Amer. Statist. Assoc. 58 415–434.
• Strobl, C., Malley, J. and Tutz, G. (2009). An Introduction to Recursive Partitioning: Rationale, Application, and Characteristics of
Classification and Regression Trees, Bagging, and Random forests. Psychological Methods, 14(4), 323–348.