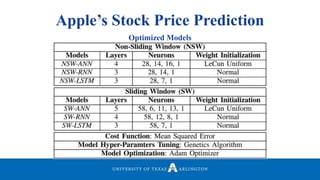
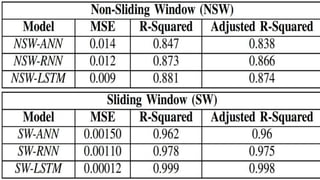
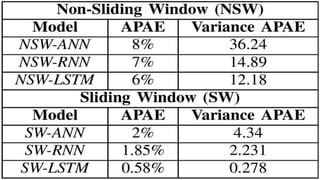
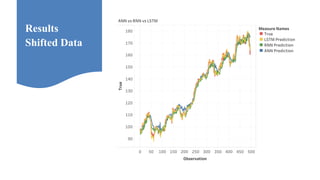
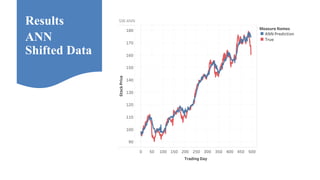
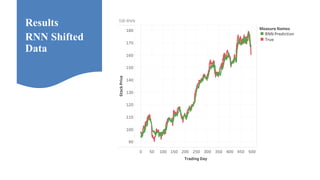
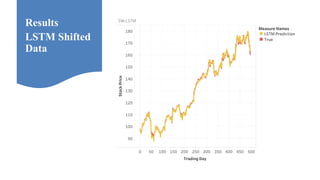
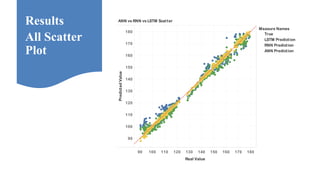
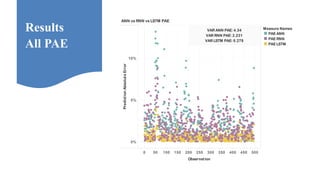
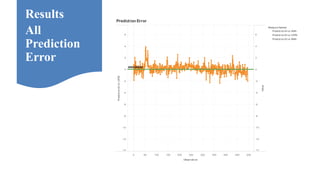
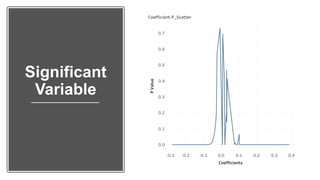
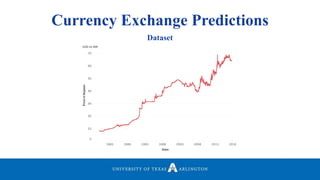
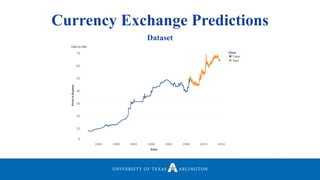
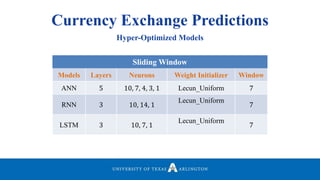
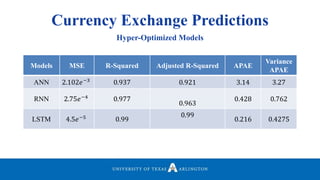
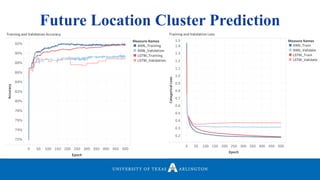
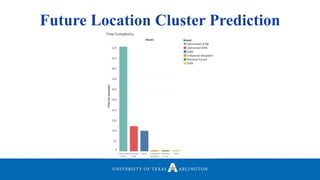
Neelabh Pant successfully defended his PhD thesis titled "Hyper-optimized Machine Learning and Deep Learning Methods for Geo-Spatial and Temporal Function Estimation" at the University of Texas at Arlington. His research focused on developing recurrent neural networks, long short-term memory models, and genetic optimization techniques to predict locations, stock prices, and currency exchanges based on spatio-temporal data. Pant's dissertation committee included Dr. Ramez Elmasri as his advisor along with four other professors who evaluated his work.

1. PhD Defense
Neelabh Pant
Mining and Analysis of Spatio-Temporal Data Lab (MAST)
Department of Computer Science and Engineering
University of Texas at Arlington
Dr. Ramez Elmasri (Advisor / Supervisor)
Mr. David Levine
Dr. Leonidas Fegaras
Dr. Sharma Chakravarthy
Dr. Shashi Shekhar
Committee Members

2. Hyper-optimized Machine Learning and Deep
Learning Methods for Geo-Spatial and
Temporal Function Estimation

3. Presentation Overview
1. Research up to Proposal (October 2017)
I. Location Prediction
i. Hidden Markov Model
a. Chinese Study
ii. Deep Neural Network
a. American Study
2. Research after Proposal (May 2018)
I. Methods:
i. Recurrent Neural Networks (RNN)
ii. Long Short Term Memory (LSTM)
iii. Genetic Optimization Technique
II. Domain:
i. Stock Prediction
ii. Currency Exchange Prediction
iii. Location Prediction
III. System
IV. Future Works
Committee’s
request
An Extra
Mile

4. Presentation Overview
1. Research up to Proposal (October 2017)
I. Location Prediction
i. Hidden Markov Model
a. Chinese Study
ii. Deep Neural Network
a. American Study
2. Research after Proposal (May 2018)
I. Methods:
i. Recurrent Neural Networks (RNN)
ii. Long Short Term Memory (LSTM)
iii. Genetic Optimization Technique
II. Domain:
i. Stock Prediction
ii. Currency Exchange Prediction
iii. Location Prediction
III. System
IV. Future Works

5.  Analysis of human movement to identify most significant places.
 Discover hidden patterns underlying in human behavior.
 Existing techniques do not focus on the time series patterns.
 High degree of freedom challenges to model human mobility.
 Abundant GPS Data gives one enough opportunity to build useful
systems.
Motivation

6. • We focused on one major type of query, i.e. predicting future location
of a user given a day (or day and time).
• Where would a user be when it is Monday?
• Where would a user be when it is Friday, 6pm?
• However, the system can also predict locations based on a user’s
current locations, for example:
• Right now (on a week day), the user is at the ERB. What is the most likely location he
will travel to next?
Motivation

7. Applications
Shared Historical GPS Data
Black Box
Predicted Location
• Shared Location Recommendation System
THINGS TO
DO
1. Store
2. …

8. Applications
• Healthcare Applications
• Traffic Planner
• Cellular Handshaking, etc.

9. • Identified clusters or locations where a user tends to visit most
frequently.
• Clusters can be named as “Home”, “Work”, “School” etc.
Table 1: Database Records of a User
Hidden Markov Model

10. • Our Varied K-Means clustering is a two step process:
1. Find the number of K or 𝜏.
2. Find the appropriate radius 𝛿 of each cluster.
HMM - (Varied K-Means Algorithm)

11. • Our variation of the K-Means algorithm was influenced by [1] and [2].
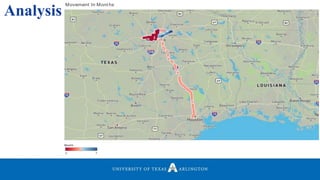
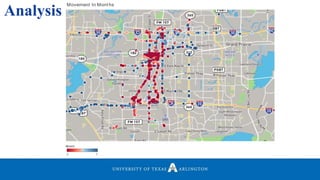
• Mainly focused on “where the user is instead of how the user got there”.
• Find the locations where a user spent most of their time.
• Targeted our algorithm to find the time elapsed between two consecutive
points.
• Identified the points which have more than “𝜏” between them and their
corresponding previous point.
• Another challenge was to find a significant value of “𝜏”.
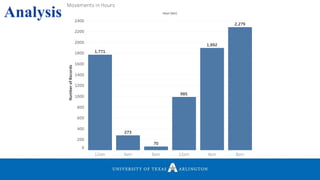
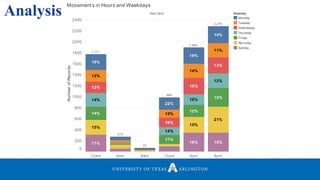
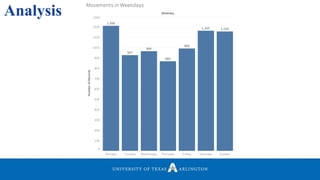
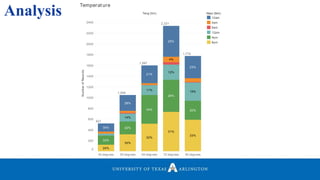
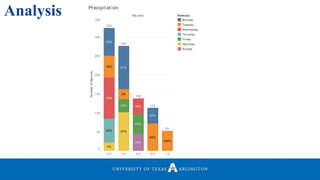
• Plotted a graph of Graph to Identify Meaningful Locations.
HMM - (Varied K-Means Algorithm)

12. Figure 1: Graph to identify meaningful locations
HMM - (Varied K-Means Algorithm)

13. • “𝜏” = 10mins. Now we start extracting the sites locations.
• Extracted sites are kept in a set which is called as significant sites.
• In traditional K-Means we need to initiate K.
• In our varied K-Means, K = Total # of extracted sites where a user
stopped for at least 10 minutes.
• K is also known as the number of desired clusters.
HMM - (Varied K-Means Algorithm)

14. • The objective of step 2 is to cluster points around the starting centroids found in step 1.
• The data is spread widely on a city-wide scale.
• Need to have a good measure of the radius for a cluster.
• If radius is too large: We will end up with insignificant places in the cluster, which will give incorrect results.
• If radius is too small: We will end up getting one single point in the cluster.
• To find an optimal radius for the cluster:
• We find distances “𝛿” between each significant centroid. Which was calculated using Haversine Distance metric.
• Extract the minimum “𝛿” and use it as the radius of the cluster.
• For different users, “𝛿” came out to be different, as one value of “𝛿” cannot be generalized for all the users.
HMM - (Varied K-Means Algorithm)

15. Figure 2: Clusters found for a user, user3 when radius=0.2 miles
K or 𝜏 = 253
𝛿 = 0.2
Figure display = 6 Ks
HMM - (Varied K-Means Algorithm)

16. Figure 3: Transition Between Clusters with Probability
HMM - (Varied K-Means Algorithm)

17. Hidden Markov Model for Days in a Week
• A, B, and C are the visible states or clusters.
• The hidden states are the days of the week.
• Thus by making use of the Bayesian Approach:
• 𝑃 𝑥 𝑆𝑢𝑛𝑑𝑎𝑦 =
𝑃 𝑆𝑢𝑛𝑑𝑎𝑦 𝑥 ∗𝑃(𝑥)
𝑃(𝑆𝑢𝑛𝑑𝑎𝑦)
• 𝑥 = ClusterID
• 𝑃 𝑆𝑢𝑛𝑑𝑎𝑦 𝑥 =
𝑇𝑜𝑡𝑎𝑙 # 𝑜𝑓 𝑣𝑖𝑠𝑖𝑡𝑠 𝑡𝑜 𝑥 𝑜𝑛 𝑆𝑢𝑛𝑑𝑎𝑦
𝑇𝑜𝑡𝑎𝑙 # 𝑜𝑓 𝑣𝑖𝑠𝑖𝑡𝑠 𝑡𝑜 𝑥
• 𝑃(𝑥) =
𝑇𝑜𝑡𝑎𝑙 𝑝𝑜𝑖𝑛𝑡𝑠 𝑖𝑛 𝑐𝑙𝑢𝑠𝑡𝑒𝑟 𝑥
𝑇𝑜𝑡𝑎𝑙 𝑝𝑜𝑖𝑛𝑡𝑠 𝑖𝑛 𝑎𝑙𝑙 𝑐𝑙𝑢𝑠𝑡𝑒𝑟𝑠
• If, 𝑋 = set of all clusters, then
• 𝑃(𝑆𝑢𝑛𝑑𝑎𝑦) = 𝑃 𝑆𝑢𝑛𝑑𝑎𝑦 𝑥 ∗ 𝑃 𝑥 + 𝑃 𝑆𝑢𝑛𝑑𝑎𝑦 𝑦 ∗
Hidden Markov Model - Day

18. Figure 5: Hidden Markov Model for Days and Time
• Example query: Where is a user most likely to
be at 8 pm on Wednesday?
• 𝑃 𝑥 𝑊𝑒𝑑𝑛𝑒𝑠𝑑𝑎𝑦. 7 =
𝑃 𝑊𝑒𝑑𝑛𝑒𝑠𝑑𝑎𝑦. 7 𝑥 ∗𝑃(𝑥)
𝑃(𝑊𝑒𝑑𝑛𝑒𝑠𝑑𝑎𝑦.7)
• This looks like a simple query but now it has
been added with an extra feature in the
calculation.
• Addition of time within the day.
• Intuitively, we are trying to calculate the
contribution of period and day together.
• To make faster calculations, we compute this
offline by running the algorithm on the entire
training data set.
Hidden Markov Model – Day and Time

19. Artificial Neural Network
• GPS data should be made private and sensitive and hence acquiring a GPS data set
that satisfies VACCU :
• Validity
• Accuracy
• Completeness
• Consistency
• Uniformity, is very difficult.
• To overcome this issue we use
• Our own personal 8 months of GPS dataset recorded on our own GPS devices.
• GeoLife Dataset by Microsoft Research Asia

20. Dataset
GeoLife Personal Data

21. Analysis

22. Analysis Hour (bin)
12am 4am 8am 12pm 4pm 8pm
0
200
400
600
800
1000
1200
1400
1600
1800
2000
2200
2400
NumberofRecords
16%
22%
16%
14%
12%
15%
14%
11%
12%
18%
15%
13%
14%
14%
10%
12%
14%
17%
12%
15%
15%
15%
21%
17% 18% 15%
1,771
273
70
985
1,892
2,279
Movement s in Hours and Weekdays
Weekday
Monday
Tuesday
Wednesday
Thursday
Friday
Sat urday
Sunday

23. Analysis

24. Analysis Weekday
Monday Tuesday Wednesday Thursday Friday Sat urday Sunday
0
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300
NumberofRecords
24%
23%
21%
29%
24%
23%
27%
30%
40%
35%
30%
18%
16%
18%
16%
17%
30%28%
24%
28%
30%
23%
22%
25%
30%
25%
8%
4%
5%
6%
5%
5%
1,208
927
964
866
989
1,162 1,154
Movement in Weekdays and Hours
Hour (bin)
12am
4am
8am
12pm
4pm
8pm

25. Analysis Tavg (bin)
40 degrees 50 degrees 60 degrees 70 degrees 80 degrees
0
200
400
600
800
1000
1200
1400
1600
1800
2000
2200
2400
NumberofRecords
30%
28%
21%
25%
23%
33%
14%
11%
12%
19%
33%
22%
34%
26%
20%
24%
30%
32%
31%
4%
521
1,049
1,597
2,331
1,772
Temperat ure
Hour (bin)
12am
4am
8am
12pm
4pm
8pm

26. Analysis Ppt (bin)
0.2 0.4 0.6 0.8 1.0
0
50
100
150
200
250
300
350
NumberofRecords
100%
41%
36%
18%
33%
64%
23%
33%
30%
20%
12%
37%
37%
7%
9%
323
276
138
113
53
Precipit at ion
Weekday
Monday
Tuesday
Wednesday
Thursday
Friday
Sat urday
Sunday

27. Analysis
Movement In Mont hs
2 7
Mont h

28. Analysis
Movement In Mont hs
2 7
Mont h

29. System
• Two Novel Different Methods to Predict Locations:
1. Multiple Linear Regression: 𝑦′
= 𝑏 + 𝑋0 𝑤 𝑜 + 𝑋1 𝑤1 + ⋯ + 𝑋 𝑛 𝑤 𝑛
2. Classification: 𝜎(𝑍) 𝑗 =
𝑒
𝑍 𝑗
𝑘=1
𝐾 𝑒 𝑍 𝐾
for 𝑗 = 1, … , 𝐾

30. System
1. Multiple Linear Regression: 𝑦′
= 𝑏 + 𝑋0 𝑤𝑜 + 𝑋1 𝑤1 + ⋯ + 𝑋 𝑛 𝑤 𝑛
• Predictive features:
1. Time
2. Weekday
3. Month
4. Temperature
5. Precipitation
• Target Feature:
• Location
• Latitude, Longitude
Multiple Linear Regression

31. System
1. Multiple Linear Regression: 𝑦′
= 𝑏 + 𝑋0 𝑤 𝑜 + 𝑋1 𝑤1 + ⋯ + 𝑋 𝑛 𝑤 𝑛
• Hypothesis:
• 𝑦′ is the linear function of 𝑋 𝜖 {𝑋0, 𝑋1, … , 𝑋 𝑛} + 𝜀 (Error).
• 𝑏 and 𝑤 𝜖 {𝑤0, 𝑤1, … , 𝑤 𝑛} control our linear hypothesis.
Multiple Linear Regression

32. System
1. Multiple Linear Regression: 𝑦′
= 𝑏 + 𝑋0 𝑤 𝑜 + 𝑋1 𝑤1 + ⋯ + 𝑋 𝑛 𝑤 𝑛
• Cost:
• Residual: 𝑦𝑖 − 𝑦′𝑖
• Total Error = 𝑖 𝜖𝑖 = 𝑖 |𝑦𝑖 − 𝑦′𝑖|
• MSE =
1
𝑁 𝑖(𝑦𝑖 − 𝑦′𝑖)2
• Why MSE?:
• Smooth and is guaranteed to have a global minimum.
Multiple Linear Regression

33. System
Multiple Linear Regression

34. System
• Softmax: 𝜎(𝑍) 𝑗 =
𝑒
𝑍 𝑗
𝑘=1
𝐾 𝑒 𝑍 𝐾
for 𝑗 = 1, … , 𝐾.
• Impart probabilities
• Gives probability distribution for each targets
• Finding out classification where probability of the class
is maximum
Classification

35. System

36. Experiments
American Study:
1. ~9000 GPS points
2. 6 Months Data
3. Google Timeline
4. Weather Added

37. Experiments
Table 1: MLR Model Configuration
Table 2: Features Set
Multiple Linear Regression

38. Experiments
Table 3: Classification Model
Classification

39. Results
1. Multi Linear Regression WITHOUT WEATHER
2. Multi Linear Regression WITH WEATHER
American Study

40. 0 10 20 30 40 50 60 70 80 90 100
Epoch
-1.63
-1.62
-1.61
-1.60
-1.59
-1.58
-1.57
-1.56
-1.55
LogLoss
-1.63
-1.62
-1.61
-1.60
-1.59
-1.58
-1.57
-1.56
-1.55
LogLoss
Loss Using Time vs Time Weat her
Measure Names
Loss Wit h BOTH Time and Weat her
Loss Wit h ONLY Time

41. 0 10 20 30 40 50 60 70 80 90 100
Epoch
-1.64
-1.63
-1.62
-1.61
-1.60
-1.59
-1.58
-1.57
-1.56
-1.55
-1.54
-1.53
-1.52
-1.51
-1.50
LogLoss
-1.64
-1.63
-1.62
-1.61
-1.60
-1.59
-1.58
-1.57
-1.56
-1.55
-1.54
-1.53
-1.52
-1.51
-1.50
LogLoss
Validat ion Loss Using Time vs Time Weat her
Measure Names
Validat ion Loss Wit h BOTH Time and Weat her
Validat ion Loss Wit h ONLY Time

42. Results
1. Classification Accuracy
2. Comparison with Oher Classifiers
American Study

44. Model
Multi Layer
Perceptron
Random Forest
Classifier
Support Vector
Machine
K - Nearest
Neighbor
0
10
20
30
40
50
60
70
80
90
AccuracyinPercent(%)
87.71637
65.96018 65.55595
58.52168
Model
Multi Layer Perceptron
Random Forest Classifier
Support Vector Machine
K - Nearest Neighbor
Table 4: Classification Report (Validation Data)
Image source: Wikipedia

45. Presentation Overview
1. Research up to Proposal (October 2017)
I. Location Prediction
i. Hidden Markov Model
a. Chinese Study
ii. Deep Neural Network
a. American Study
2. Research after Proposal (May 2018)
I. Methods:
i. Recurrent Neural Networks (RNN)
ii. Long Short Term Memory (LSTM)
iii. Genetic Optimization Technique
II. Domain:
i. Stock Prediction
ii. Currency Exchange Prediction
iii. Location Prediction
III. System
IV. Future Works

46. Presentation Overview
1. Research up to Proposal (October 2017)
I. Location Prediction
i. Hidden Markov Model
a. Chinese Study
ii. Deep Neural Network
a. American Study
2. Research after Proposal (May 2018)
I. Methods:
i. Recurrent Neural Networks (RNN)
ii. Long Short Term Memory (LSTM)
iii. Genetic Optimization Technique
II. Domain:
i. Stock Prediction
ii. Currency Exchange Prediction
iii. Location Prediction
III. System
IV. Future Works

47. Recurrent Neural Network
1. Unlike ANNs, RNNs have hidden state.
2. Hidden state make them to store important
information about past.
3. RNNs are dynamic neural network:
• The output depends on current input as well the past
hidden state.

48. Recurrent Neural Network
1. At time step t the model:
• Processes the input vector x(t)
• Calculates the hidden state h(t)
• To predict the output y(t)

49. Recurrent Neural Network
RNNs however suffer from a fundamental problem:
1. Not being able to capture Long Term Dependency
2. Vanishing gradient problem
• The gradient exponentially decays as it’s back-propagated
3. Factors that affect the magnitude of gradient
1. Weights
2. Derivatives of activation function
4. If either of these factors are smaller than 1 gradients may vanish in time
5. To overcome this problem we introduce LSTM

50. Long Short Term Memory (LSTM)
LSTM cell consists of three gates:
1. Input Gate
2. Output Gate
3. Forget Gate
• A gate is just like a layer (f(Input*Weight + Bias))
• Each gate has weights associated.
• Hence an LSTM cell is fully differentiable.
• We can compute the derivative of the components (gates).
• That will help us make them learn the information over time.

51. LSTM – Forget Gate
Sigmoid layer:
𝑓𝑡 = 𝜎(𝑊𝑓. ℎ 𝑡−1, 𝑥𝑡 + 𝑏𝑓)
1. Takes Output at time ‘t-1’, and
2. Current input at time ‘t’
3. Multiplied with internal state (𝐶𝑡−1)
4. If 𝑓𝑡 = 0, internal state is forgotten,
else
5. Internal state 𝐶𝑡−1 is passed
unaltered

52. LSTM – Input Gate
Sigmoid layer:
𝑖 𝑡 = 𝜎(𝑊𝑖. ℎ 𝑡−1, 𝑥𝑡 + 𝑏𝑖)
1. Takes Output at time ‘t-1’, and
2. Current input at time ‘t’
3. Multiplied with the output of
candidate layer
𝐶𝑡 = tanh(𝑊𝑐. ℎ 𝑡−1, 𝑥𝑡 + 𝑏 𝑐)

53. LSTM – State Update
Internal State is updated with this
rule:
𝐶𝑡 = 𝑓𝑡 ∗ 𝐶𝑡−1 + 𝑖 𝑡 ∗ 𝐶𝑡
The previous state
is multiplied by the
forget gate
Then added to the
fraction of the new
candidate allowed by
the input

54. LSTM – Output Gate
Output Gate controls how much of the
internal state is passed to the output
𝑜𝑡 = 𝜎(𝑊𝑜. ℎ 𝑡−1, 𝑥𝑡 + 𝑏 𝑜)
ℎ 𝑡 = 𝑜𝑡 ∗ tanh(𝑐𝑡)
This way the network learns:
i. How much the past output to keep
ii. How much of the current input to keep,
and
iii. How much of the internal state to send
out to the output

55. Optimization
1. Heuristics
2. Meta-heuristics
Heuristics:
Technique, which seeks optimal or near optimal solutions at a reasonable computational
cost
Meta-Heuristics:
Heuristics that are inspired by nature and are not problem specific

56. Optimization
• An example of metaheuristics is Genetics Algorithm.
• Higher level procedure to find or generate heuristic partial search algorithm
• GA’s mostly deal with optimization, to get as close to an ideal solution as
possible
• Specially with incomplete/imperfect information or limited computational
capacity
Genetic Algorithm

57. Optimization
• Samples a set of solutions, which is too large to be completely
sampled.
• Compared to optimization algorithm, e.g. Grid Search, metaheuristics
cannot guarantee a globally optimal solution.
• Provides a list of “good” solutions, not just a single solution.
Genetic Algorithm

58. Optimization
• Survival of the fittest
• Individual in a population exhibit variation in appearance
and behavior
• Those with traits most fitting in the environment survive to
reproduce
• Some of those traits are passed down from generation to
generation, including mutation to offer more variation in
the future
Darwin’s Famous Theory of Evolution

59. Optimization
• Developed by John Holland in the 1970
• Belongs to larger class of Evolutionary Algorithm
• Inspired by evolution, more specifically natural
selection, reproduction, and survival of the fittest
• Parents and offspring (organisms)
• Genetic crossover, mutation and selection
Genetics Algorithm

60. Select
𝑀, 𝑁, 𝑝𝑐, 𝑝 𝑚
and 𝑘
Create a
population of 𝑁
Pick at random
𝑘 strings
Evaluate and
pick best one
Twice
2
parents
Crossover at
𝑝𝑐
2
childrenMutate at 𝑝 𝑚
2
mutated
children
Is
𝑛 =
𝑁/2
𝑛 = 𝑛 + 1
Is
m =
𝑀
No
Yes
No
Yes
End, return
final set

61. Experiments
Three sets of domain and experiments
1. Apple Stock Price Prediction
2. Currency Exchange Prediction
3. Location Prediction

62. Experiments
Apple’s Stock Price Prediction
Forecast of stocks can be considered in two categories:
1. Technical Analysis
2. Fundamental Analysis
Technical Analysis:
• If dependent only on historical data (past stock value, volume of stocks etc.)
Fundamental Analysis:
• If dependent on external affects, e.g.:
i. Currency exchange rates
ii. News
iii. Interest rates

63. Used a hybrid approach considering
both technical and fundamental analysis
A total of:
i. 19 independent variables
ii. 1 dependent variable (Apple’s
closing)
High positive a negative correlation
among the variables.

64. Experiments
Apple’s Stock Price Prediction – Data/Feature Engineering
The experiments are done using:
1. Non-Sliding Window method and
2. Sliding Window method
Close Volume High Low Dependent
X11 X21 X31 Xn1 Y1 = X12
X12 X22 X32 Xn2 Y2 = X13
X13 X23 X33 Xn3 Y3 = X14

65. Experiments
Apple’s Stock Price Prediction – Data/Feature Engineering
The experiments are done using:
1. Non-Sliding Window method and
2. Sliding Window method
Close_1 Close_2 Volume High Low Dependent
X11 X10 X21 X31 Xn1 Y1 = X12
X12 X11 X22 X32 Xn2 Y2 = X13
X13 X12 X23 X33 Xn3 Y3 = X14

66. Experiments
Size of Sliding Window
• Set the window size using Partial Autocorrelation
• Partial Autocorrelation between stock prices
• Lags ranging between 10 through 40 days
• Best window size of 30 days

67. Apple’s Stock Price Prediction
Neurons/Cells and Layers Optimization
6 8 10 12 14 16 18 20
Neurons
1.5e-04
1.6e-04
1.6e-04
1.6e-04
1.7e-04
1.8e-04
Loss
0.00015109
Number of Neurons vs Loss (Hidden 2)
6 8 10 12 14 16 18 20
Neurons
0.00150
0.00152
0.00154
0.00156
0.00158
0.00160
0.00162
0.00164
0.00166
0.00168
0.00170
0.00172
0.00174
Loss
0.0015300
Number of Neurons vs Loss (Hidden 1)
0 2 4 6 8 10 12 14 16 18 20 22
Cells
1.5e-04
1.6e-04
1.6e-04
1.7e-04
1.7e-04
1.8e-04
1.8e-04
1.9e-04
Loss
0.00015320
LSTM Cells

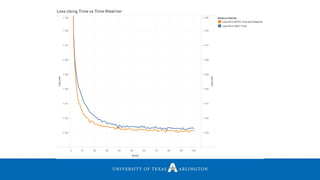
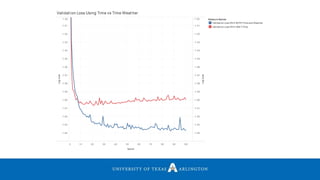
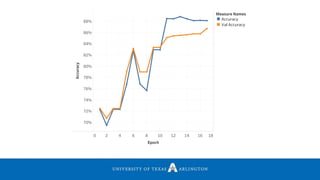
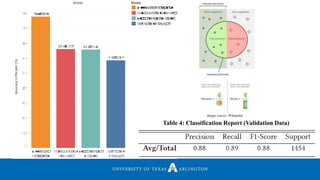
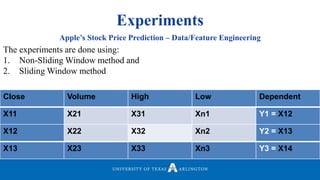
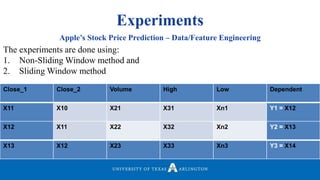
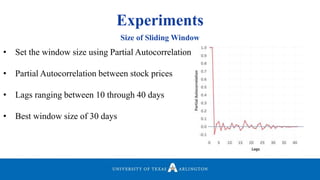
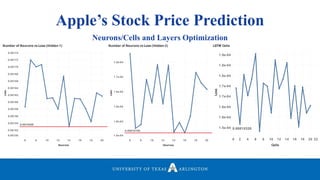
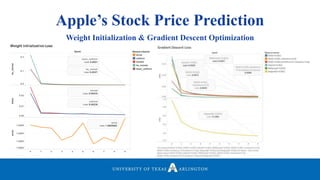
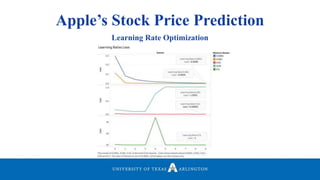
68. Experiments
Weight Initialization and Gradient Descent
• 𝑍 = 𝑤1 𝑥1+ 𝑤2 𝑥2 + ⋯ + 𝑤 𝑛 𝑥 𝑛
• Good rule of thumb:
• Var(𝑊𝑖) =
1
𝑛
• Set variance of weights equal to
1/number of features in the dataset
• Lecun_Uniform: Named after its creator
Yann LeCun
• Lecun_uni: Draws samples from
uniform distribution within [-lim, lim]
• lim = 𝑠𝑞𝑟𝑡(
3
𝑓𝑎𝑛𝑖𝑛
)
• He_normal: Named after its creator
Kaiming He
• StdDev(𝑊𝑖) = 𝑠𝑞𝑟𝑡(
2
𝑓𝑎𝑛𝑖𝑛
)

69. Experiments
Weight Initialization and Gradient Descent

70. Apple’s Stock Price Prediction
Weight Initialization & Gradient Descent Optimization
Epoch
0 1 2 3 4 5 6 7 8 9
0.0
0.1
0.2
he_normal
0.00
0.01
0.02
Value
1.0002
1.0003
1.0004
1.0005
zeros
lecun_uniform
Loss: 0.0021
he_normal
Loss: 0.0027
normal
Loss: 0.00233
uniform
Loss: 0.00238
zeros
Loss: 1.0005862
Weight Initialization Loss
Measure Names
zeros
uniform
normal
he_normal
lecun_uniform

71. Apple’s Stock Price Prediction
Learning Rate Optimization

72. Apple’s Stock Price Prediction
Optimized Models

73. Results
Evaluation of the model is done using:
1. Mean Squared Error
2. R-Squared Value
3. Adjusted R-Squared Value
4. Average Prediction Absolute Error (APAE)
5. Variance among APAE

75. Results

76. Results
Shifted Data

77. Results
ANN
Shifted Data

78. Results
RNN Shifted
Data

79. Results
LSTM Shifted
Data

80. 90 100 110 120 130 140 150 160 170 180
Real Value
90
100
110
120
130
140
150
160
170
180
PredictedValue
ANN vs RNN vs LSTM Scatter
Measure Names
True
LSTM Prediction
RNN Prediction
ANN Prediction
Results
All Scatter
Plot

81. 0 50 100 150 200 250 300 350 400 450 500
Observation
0%
5%
10%
PredictionAbsoluteError
VAR ANN PAE: 4.34
VAR RNN PAE: 2.231
VAR LSTM PAE: 0.278
ANN vs RNN vs LSTM PAE
Measure Names
PAE ANN
PAE RNN
PAE LSTM
Results
All PAE

82. 0 50 100 150 200 250 300 350 400 450 500
Observat ion
-14
-12
-10
-8
-6
-4
-2
0
2
4
6
PredictionErrorLSTM
-14
-12
-10
-8
-6
-4
-2
0
2
4
6
Value
ZERO ERROR
Prediction Error
Measure Names
Predict ion Error ANN
Predict ion Error LSTM
Predict ion Error RNN
Results
All
Prediction
Error

83. Variables
Apple_High
Apple_Open
Apple_Low
shift_23
IBM_High
SP_High
shift_25
shift_3
shift_16
IBM_Close
shift_30
shift_10
SP_Close
IBM_Volume
shift_17
shift_1
shift_18
Msft_High
IBM_Low
shift_14
Msft_Close
shift_2
shift_5
SP_Volume
shift_24
shift_6
Constant
shift_15
Msft_Low
shift_29
shift_19
shift_28
shift_13
shift_26
shift_12
shift_11
shift_9
shift_22
shift_8
shift_20
Msft_Volume
IBM_Open
shift_21
shift_7
shift_27
shift_4
SP_Low
Apple_Volume
SP_Open
Msft_Open
-0.3
-0.2
-0.1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
P Value
-0.3
-0.2
-0.1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Coefficients
Coefficients vs P-Value
Measure Names
Coefficients
P Value
Significant Variable

84. Significant
Variable

85. Currency Exchange Predictions
Dataset

86. Currency Exchange Predictions
Dataset

87. Currency Exchange Predictions
Dataset

88. Currency Exchange Predictions
Hyper-Optimized Models
Sliding Window
Models Layers Neurons Weight Initializer Window
ANN 5 10, 7, 4, 3, 1 Lecun_Uniform 7
RNN 3 10, 14, 1
Lecun_Uniform
7
LSTM 3 10, 7, 1
Lecun_Uniform
7

89. Currency Exchange Predictions
Hyper-Optimized Models
Models MSE R-Squared Adjusted R-Squared APAE
Variance
APAE
ANN 2.102𝑒−3
0.937 0.921 3.14 3.27
RNN 2.75𝑒−4
0.977
0.963
0.428 0.762
LSTM 4.5𝑒−5
0.99
0.99
0.216 0.4275

90. Results
ANN vs RNN vs LSTM Predictions
0.80 0.85 0.90 0.95 1.00 1.05 1.10 1.15 1.20 1.25 1.30 1.35 1.40
True
0.80
0.85
0.90
0.95
1.00
1.05
1.10
1.15
1.20
1.25
1.30
1.35
1.40
True
ANN vs RNN vs LSTM Scatter
Measure Names
True
LSTM prediction
RNN prediction
ANN prediction

91. Results
ANN vs RNN vs LSTM Prediction Error
0 200 400 600 800 1000 1200 1400 1600 1800 2000
Observation
0%
1%
2%
3%
4%
5%
6%
7%
8%
9%
PredictionAbsoluteError
Absolute Prediction Error
Measure Names
PAE Error LSTM
PAE Error RNN
PAE Error ANN

92. Future Location Cluster Prediction
Optimized ANN and LSTM

93. Future Location Cluster Prediction
Clusters
• Varied K-Means algorithm
• Found 8 and 10 as optimal
number of clusters
• Clusters were named manually
after inspection
• Objective is to predict the next
cluster of the user based on
time, day and weather
information

94. Future Location Cluster Prediction

95. Future Location Cluster Prediction
Model Precision Recall F-1 Score Support
Optimized
LSTM
89% 91% 0.90 806
Optimized
ANN
88% 90% 0.89 806
ANN 74% 85% 0.79 806

96. Future Location Cluster Prediction

97. System
1. Language/Visualization:
1. MATLAB/Octave
2. Python
3. Tableau
2. Deep Learning:
1. NN Toolbox (MATLAB)
2. Tensorflow(r1.6)
3. Keras (2.0.4)
3. GPU: On demand cloud-computing
1. AWS – Tesla v100 GPU
• p3.2xlarge, 1, 16GiB GPU Mem., 8 CPUs, 61GiB Main Mem.
2. Azure (Recent)
4. OS:
• LINUX

98. Future Works
Show Results in Tableau **

99. Research Papers
1. Conference:
1. Survey on Spatio-Temporal Database Research (ACIIDS 2018, Springer)
2. Performance Comparison of Spatial Indexing Structures for Different Query Types
(IRF, 2016)
3. Hyper-Optimized Deep Learning Models to Predict Future Apple’s Stocks (ICDM’18 –
in progress)
2. Workshop:
1. Detecting Meaningful Places and Predicting Locations Using Varied K-Means and
Hidden Markov Model (SIAM, 2017)
3. Journal:
1. Survey on Spatio-Temporal Database Research Extended with Deep Learning
Prediction Methods for Spatial and Temporal Data (Taylor & Francis 2018 - in progress)