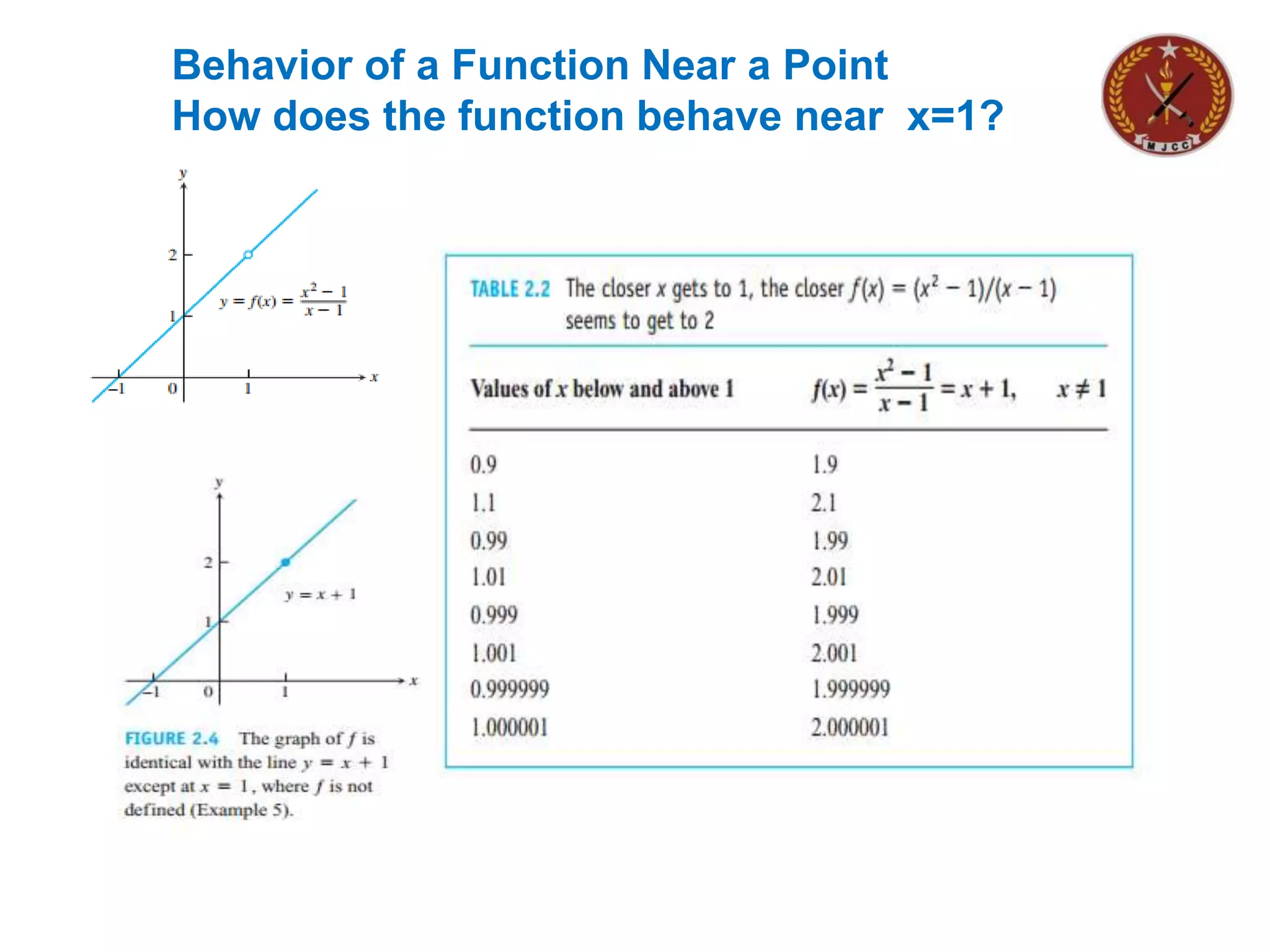
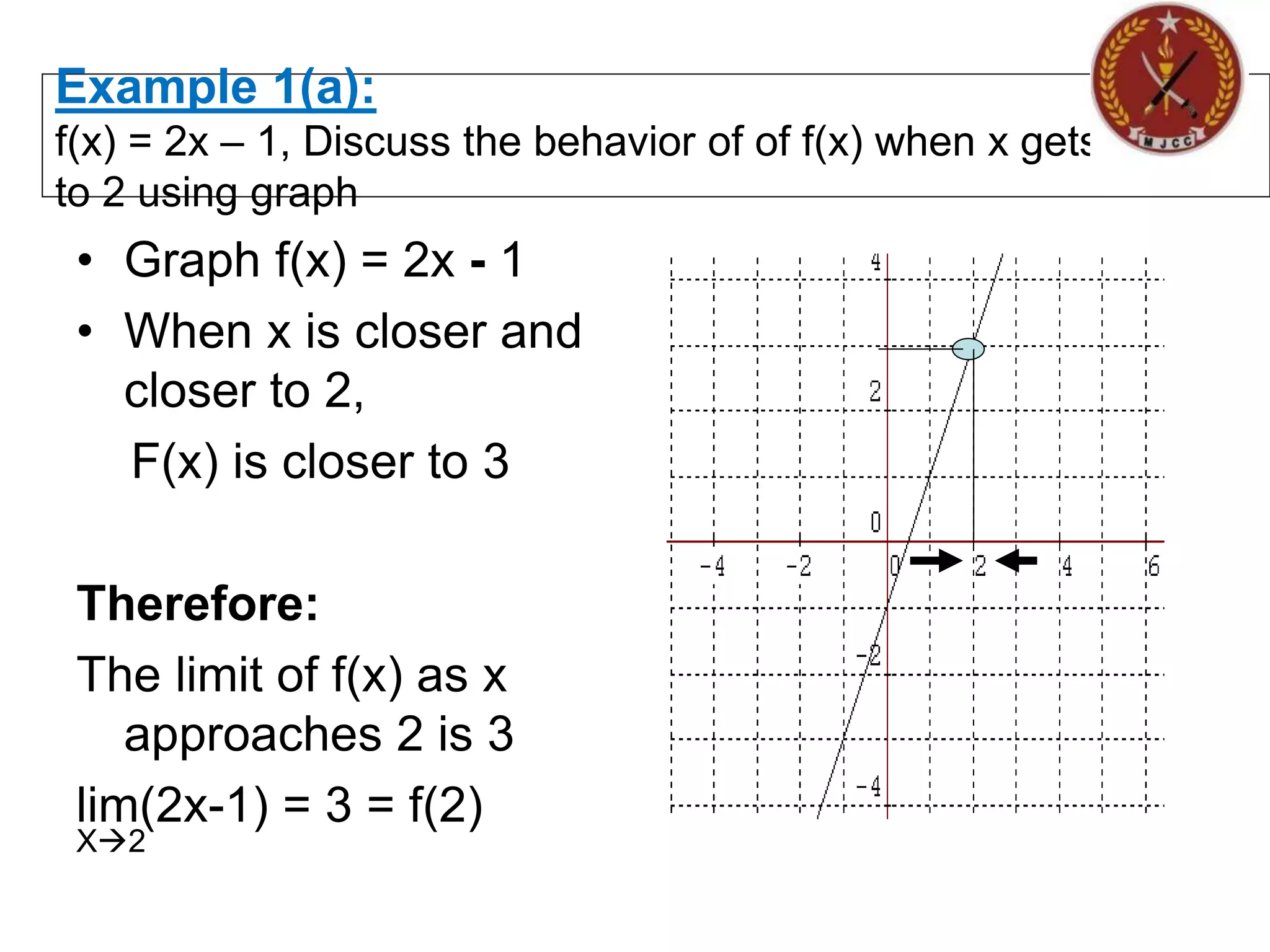
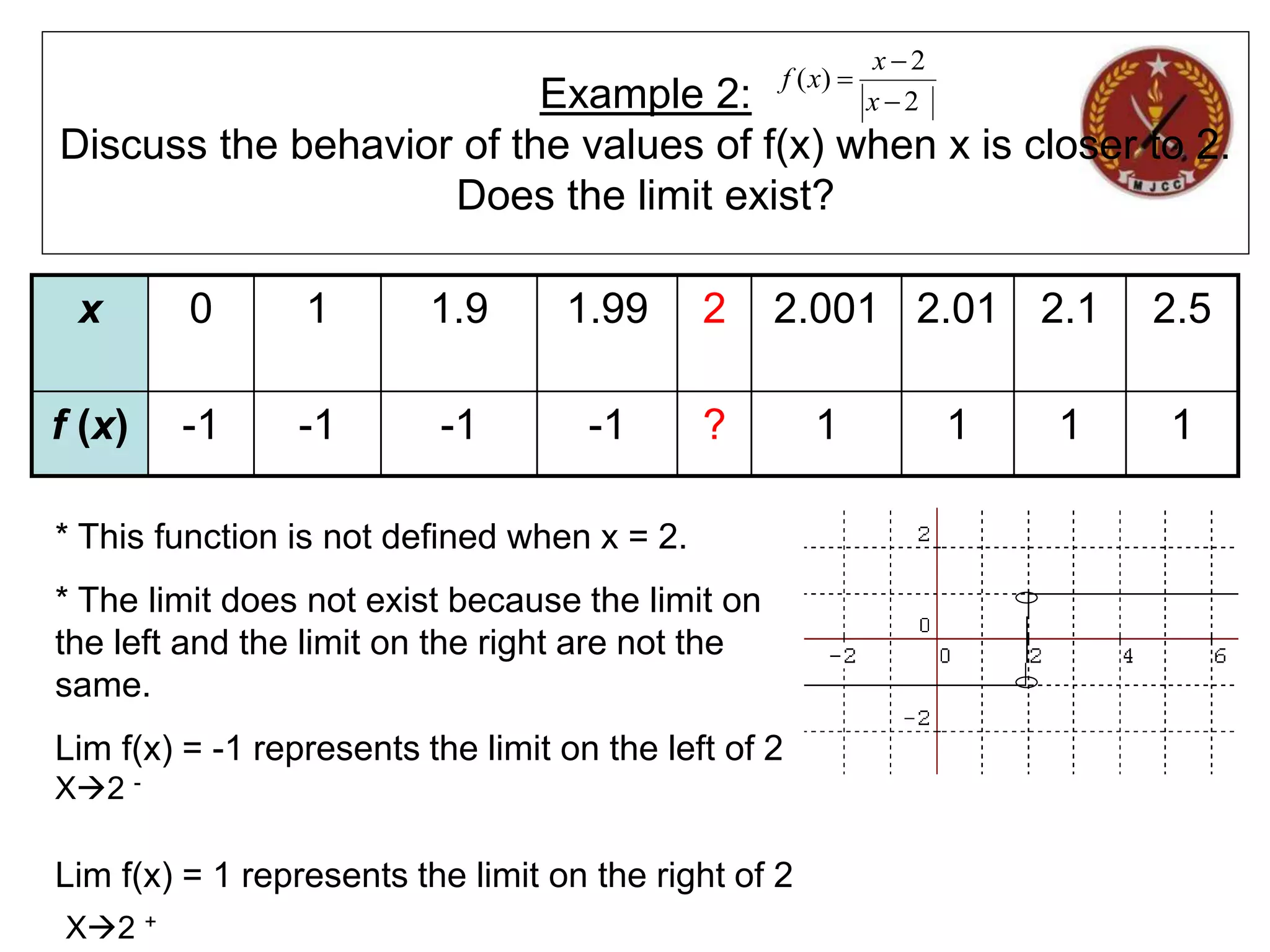
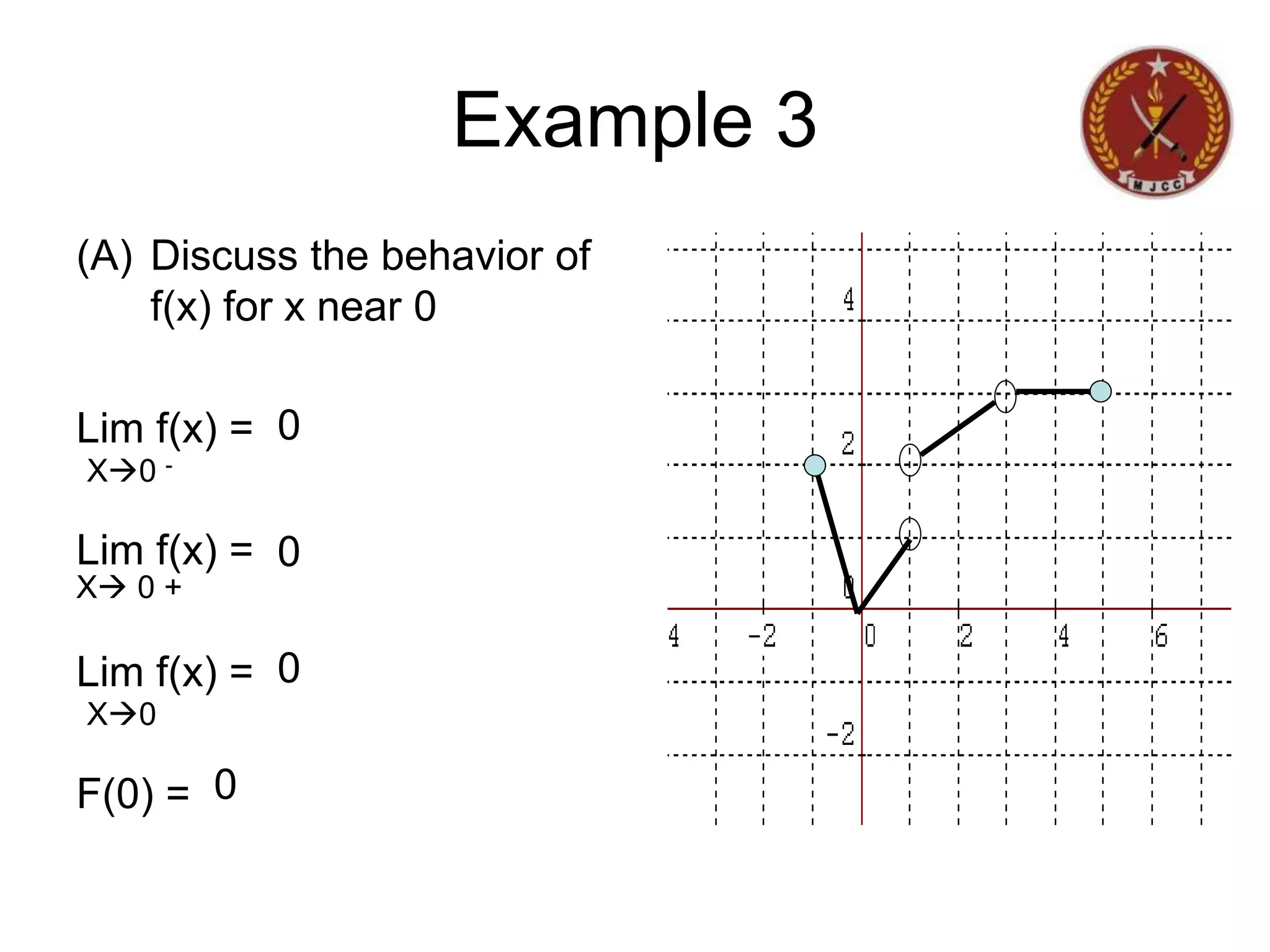
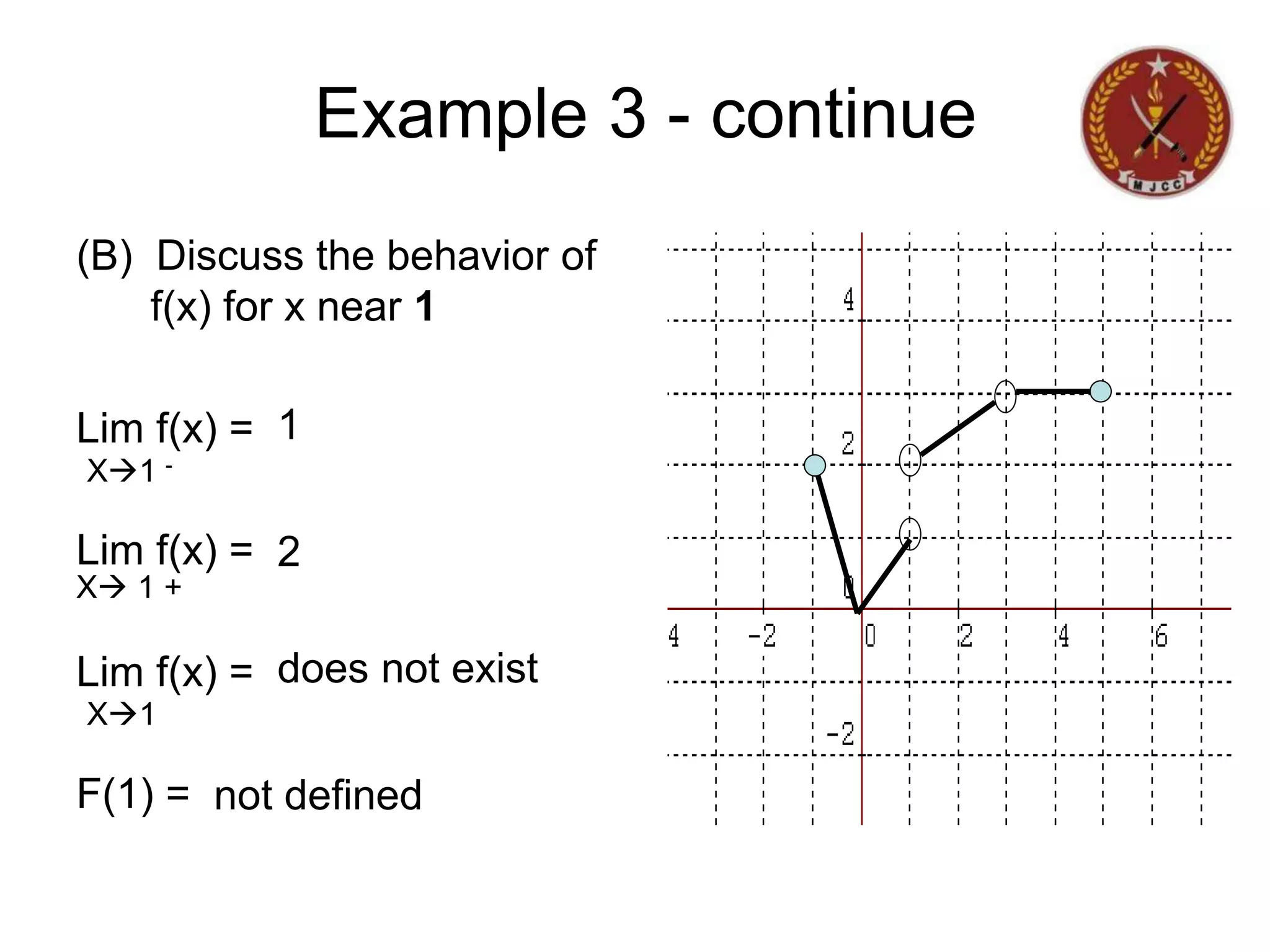
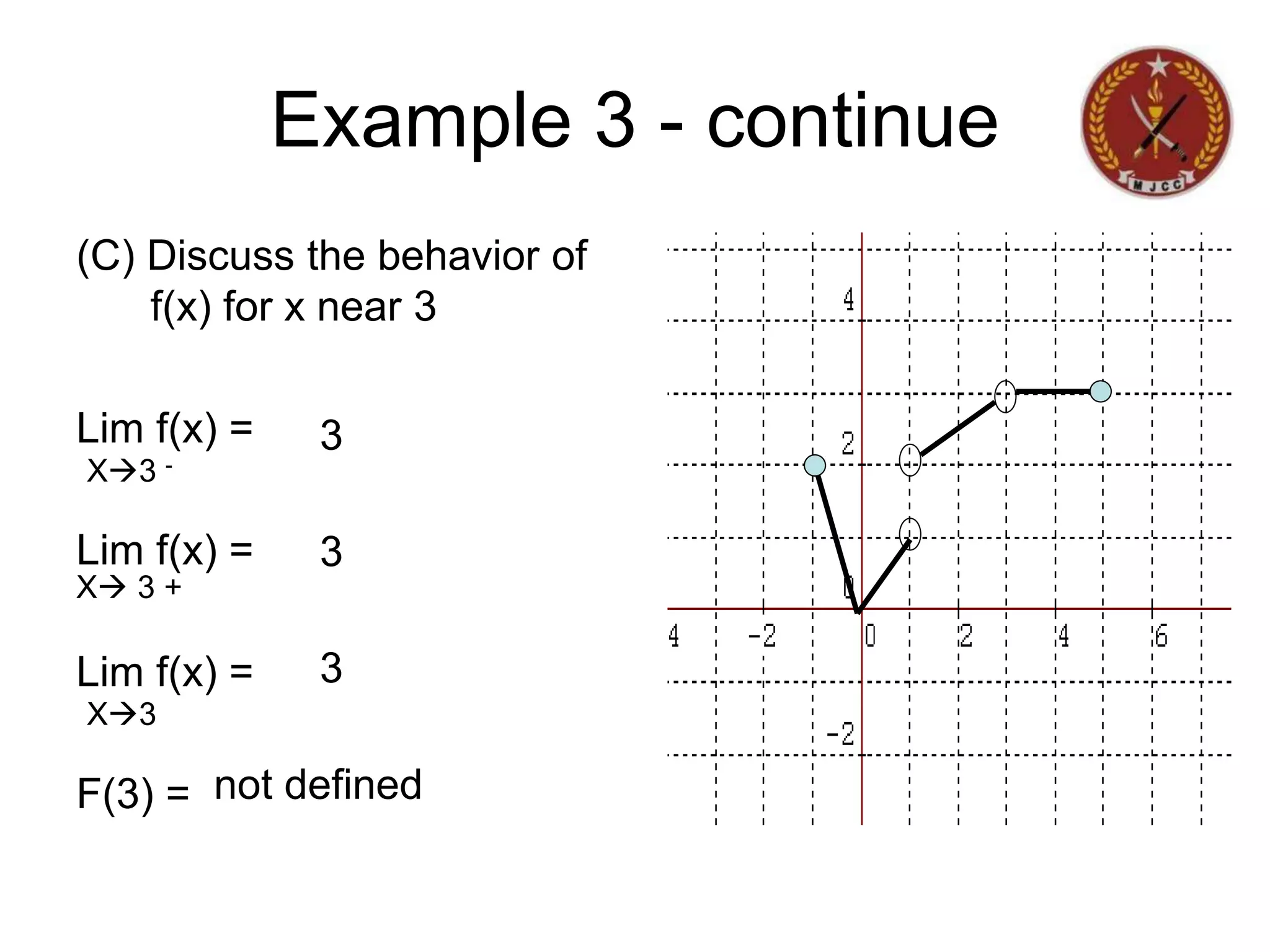
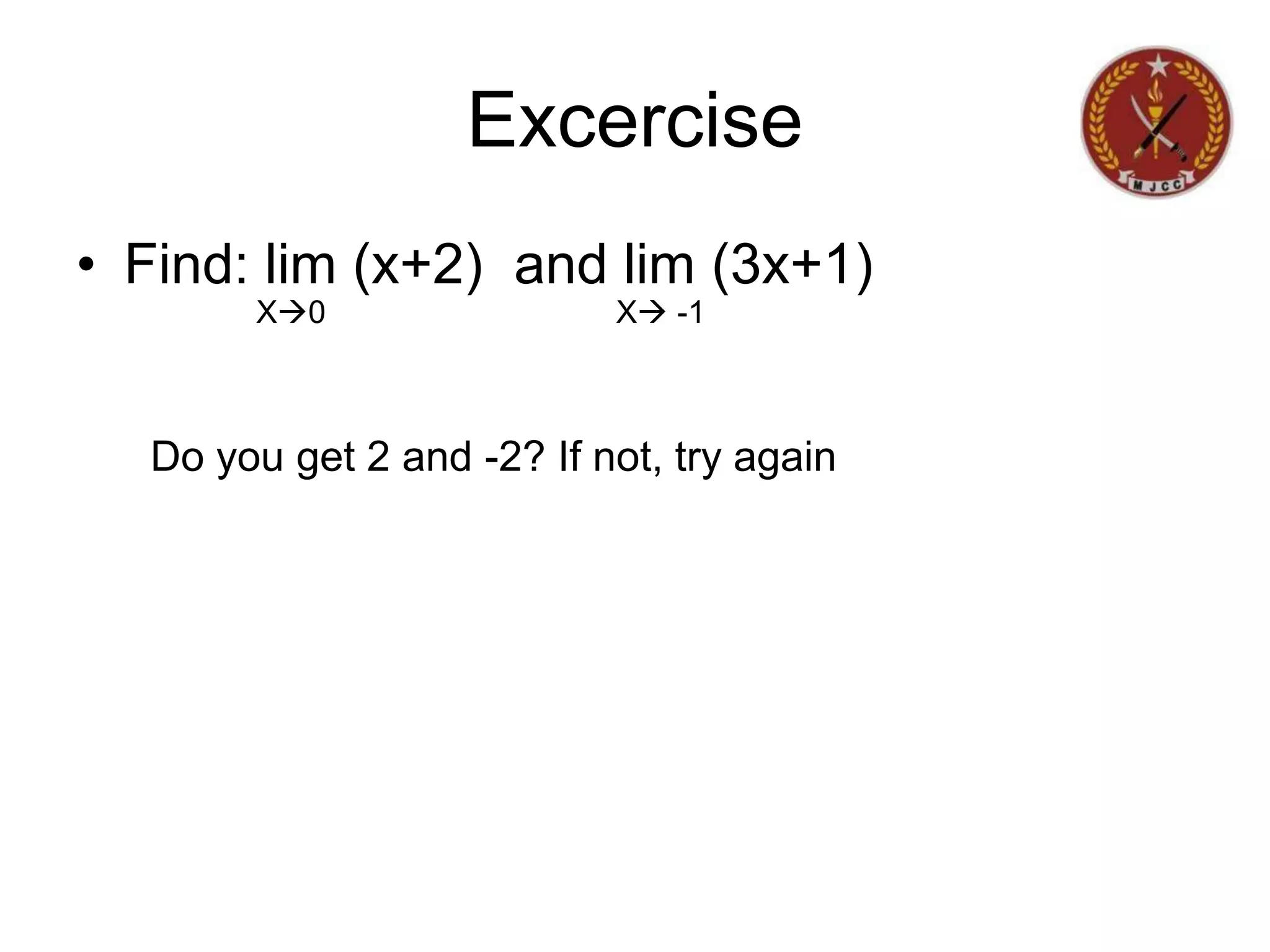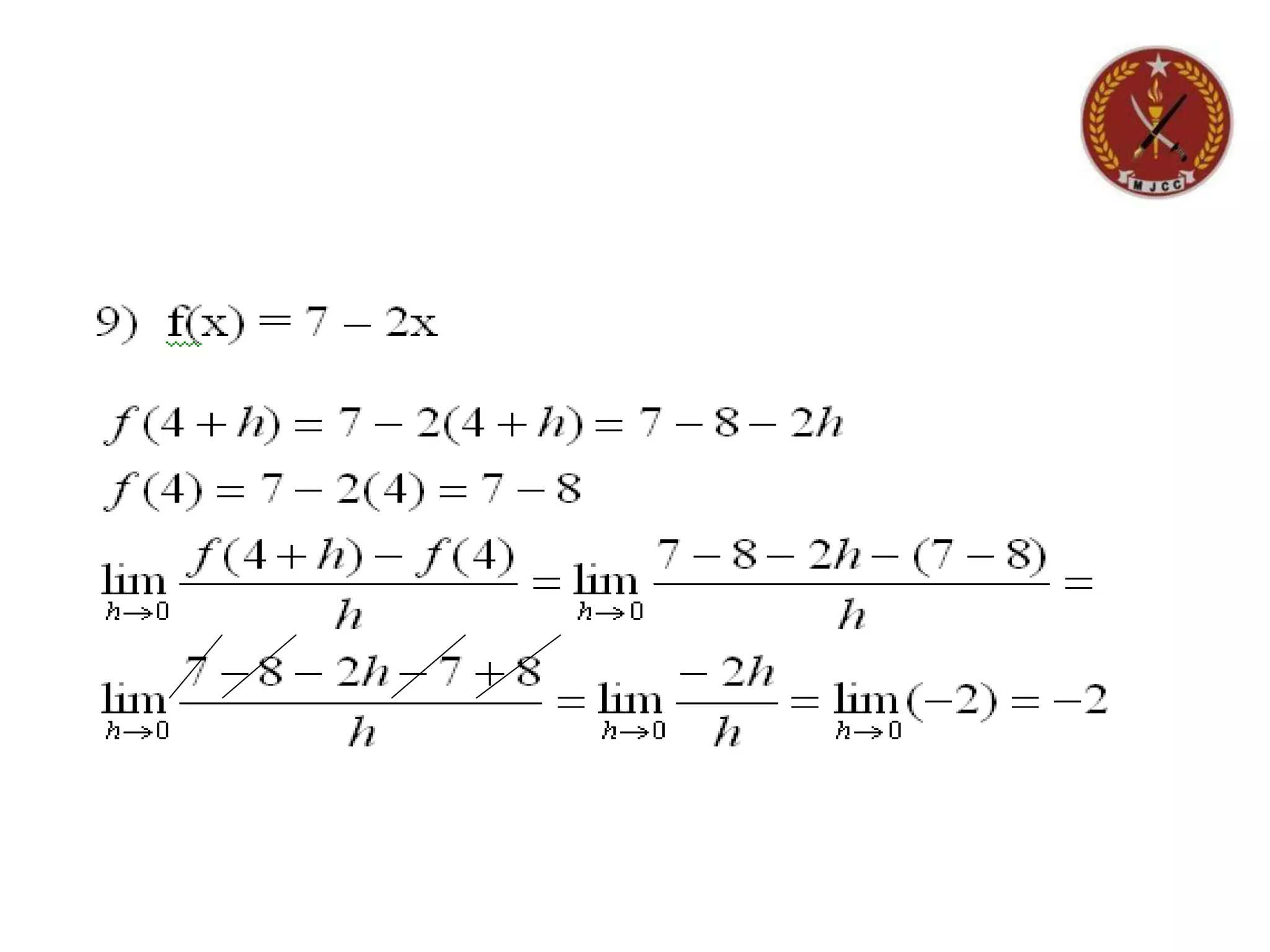The document discusses limits of functions. It begins by defining key terms like "x approaches zero" and outlines learning outcomes related to limits. Examples are provided to illustrate calculating average and instantaneous rates of change using limits, as well as one-sided limits. The document explains that a limit exists only if the left-hand and right-hand limits are equal. Several examples demonstrate evaluating limits algebraically and graphically for various functions, including limits of rational functions. The document concludes by discussing indeterminate forms that arise when evaluating certain limits.

1. LIMIT OF FUNCTIONS
BY
Mr.Sadiq Hussain
C.C.GHAZI

2. Prior knowledge
• What is “calculus”?
• What do you learn in a calculus class?
• How do algebra and calculus differ?
 You will be able to answer all of these
questions after you finish the course.

3. Learning Outcomes
• Student will learn meaning of the phrase “x
approaches zero”
• Meaning of the phrase “x approaches a”
• Meaning of the phrase “x approaches
infinity”
• Concept of Limit of a Function
• Understand Theorems on Limits of Functions
• Limits of important functions
• Method for evaluating the limits
• Practical examples for practice

4. • One of the basic concepts to the study of
calculus is the concept of limit.
• It is fundamental to finding the tangent to a
curve or the velocity of
an object.
• This concept will help to describe the
behavior of f(x) when x is approaching a
particular value c.
• In this section, we will review and learn more
about functions, graphs, and limits

5. It is fundamental to finding the tangent to a curve
or the velocity of an object. We use limits to
describe the way a function ƒ varies. Some
functions vary continuously;
small changes in x produce only small changes in
ƒ(x). Other functions can have values that jump or
vary erratically.The notion of limit gives a precise
way to distinguish between these behaviors.

6. Average and Instantaneous Speed
A moving body’s average speed during an
interval of time is found by dividing the distance
covered by the time elapsed. The unit of measure is
length per unit time: kilometers per hour, feet per
second, or whatever is appropriate to the problem
at hand.

7. EXAMPLE 1;
Finding an Average Speed A rock breaks loose
from the top of a tall cliff. What is its average speed
(a) during the first 2 sec of fall?
(b) during the 1-sec interval between second 1 and
second 2?
Solution ;
In solving this problem we use the fact, discovered
by Galileo in the late sixteenth century, that a solid
object dropped from rest (not moving) to fall freely
near the surface of the earth will fall a distance
proportional to the square of the time it has been
falling. (This assumes negligible air resistance to
slow the object down and that gravity is the only
force acting on the falling body. We call this type of
motion free fall.)

8. If y denotesthe distance fallen in feet after t
seconds, then Galileo’s law is
y = 16t^2.,
where 16 is the constant of proportionality.
The average speed of the rock during a given time
interval is the change in distance, ∆y divided by the
length of the time interval, ∆t.
(a) For the first 2 sec:
(b)From sec 1 to sec 2:

9. EXAMPLE 2; Finding an Instantaneous Speed
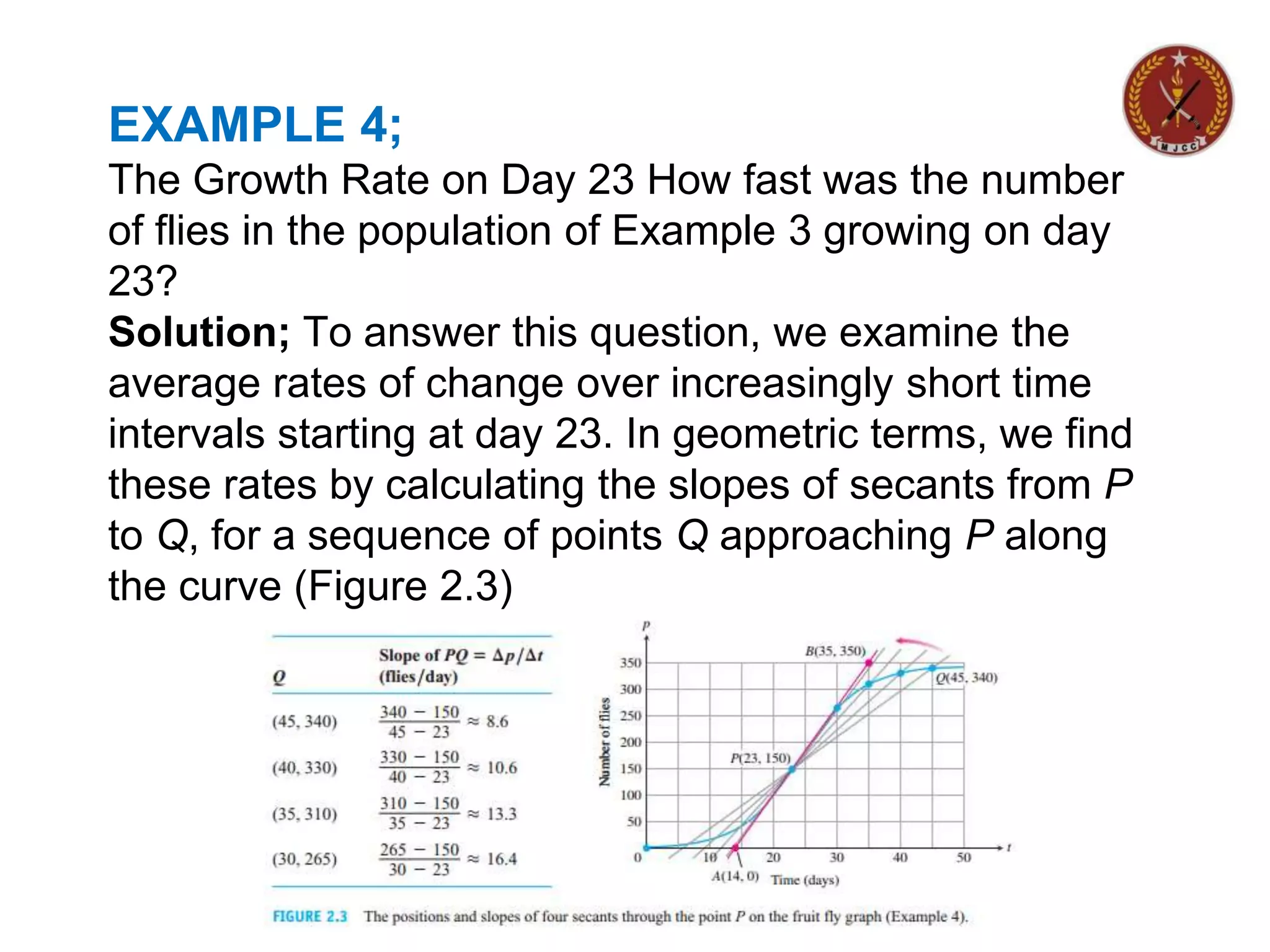
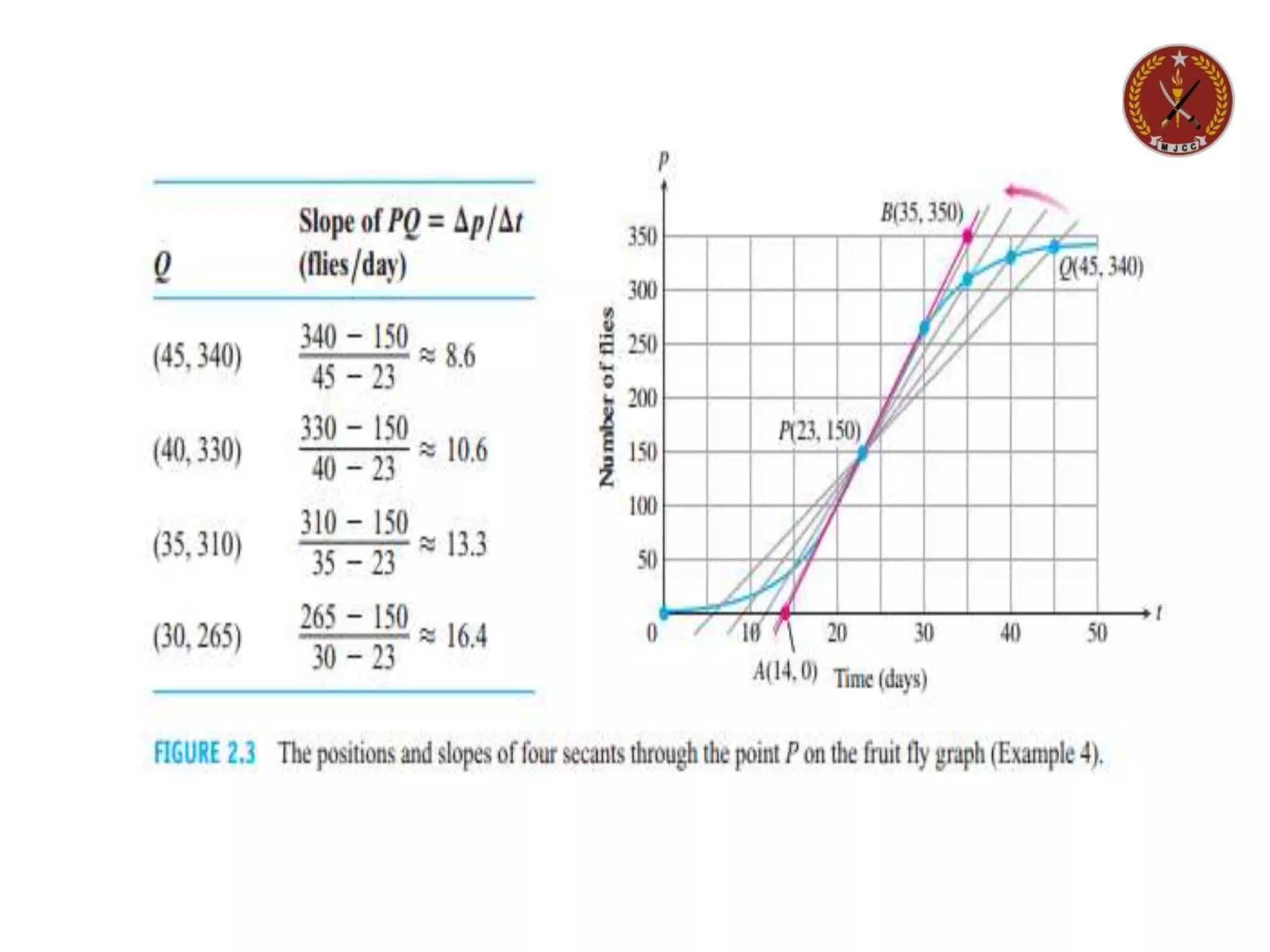
The next example examines what happens when we look at
the average speed of a falling object over shorter and
shorter time intervals
Find the speed of the falling rock at t=1sec and t=2 sec.
Solution ; We can calculate the average speed of the rock
over a time interval [t0 t0+h] having length ∆t=h as
eq(1).
We cannot use this formula to calculate the “instantaneous” speed
at t0 by substituting h=0 because we cannot divide by zero. But we
can use it to calculate average speeds over increasingly short time
intervals starting at t0=1 &t0=2 and When we do so, we see a pattern
inTable

10. The average speed on intervals starting at t0=1 seems to
approach a limiting value of 32 as the length of the interval
decreases. This suggests that the rock is falling at a speed of
32 ft sec at t0=1sec. Let’s confirm this algebraically.

11. If we set and then expand the numerator in Equation
(1) and simplify, we find that
For values of h different from 0, the expressions on the right and left
are equivalent and the average speed is32+16h ft/sec. We can now
see why the average speed has the limitingvalue 32+16(0)=32 ft/sec.
as h approaches 0.
Similarly, setting t0=1 in Equation (1), the procedureyields
for values of h different from 0. As h gets closer and closer to 0,
the average speed at t0=2 sec has the limiting value 64 ft sec.

12. Average Rates of Change and Secant Lines
Given an arbitrary function y=f(x). we calculate the average
rate of change of y with
respect to x over the interval [x1 x2], by dividing the change in
the value of y, ∆y=f(x2)-f(x1).by the length
∆x=x2-x1=h of the interval over which the
change occurs.

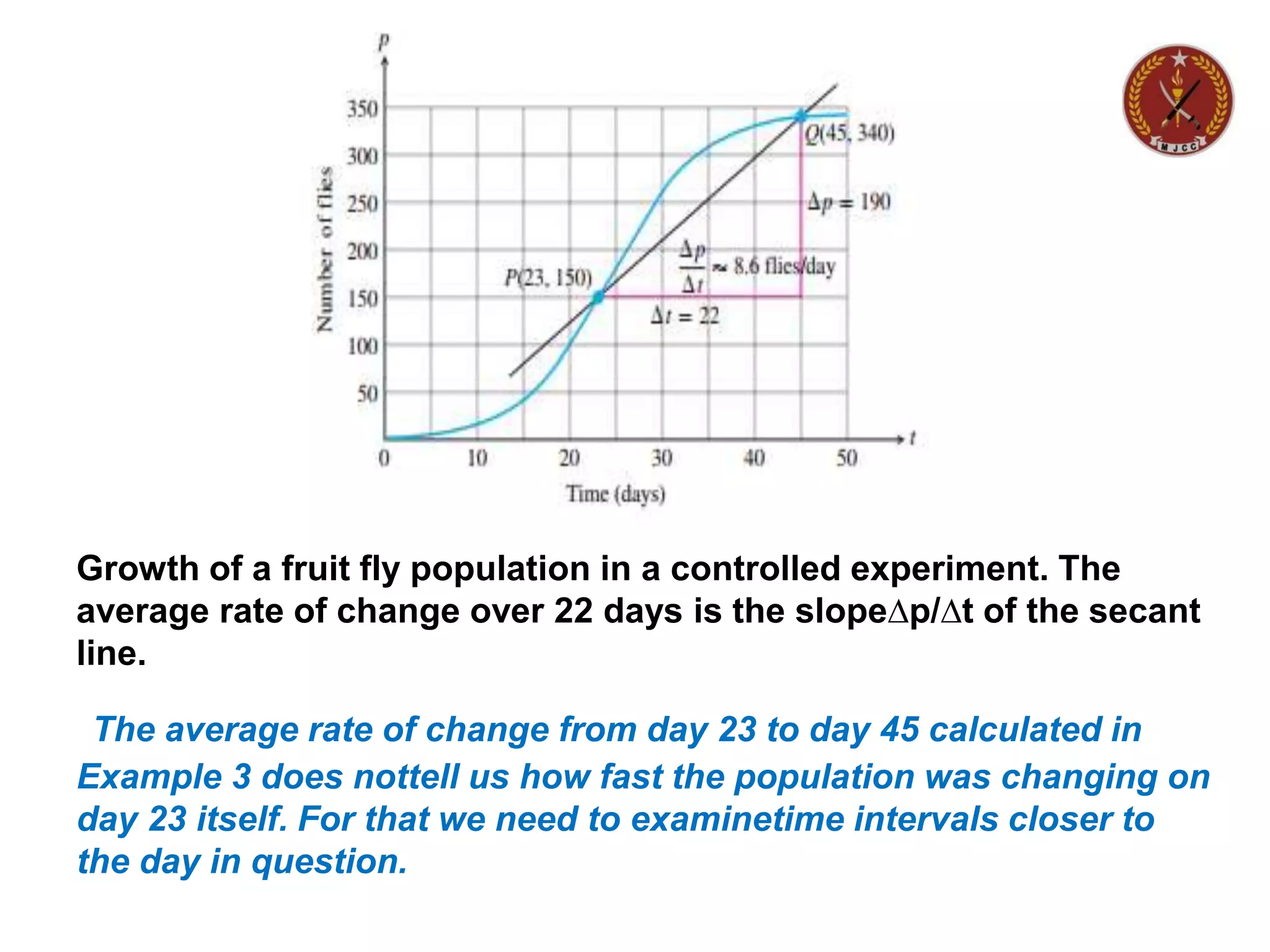
13. Conclusion;
Geometrically, the rate of change of ƒ over [x1 x2], is the slope of
the line through the pointsP(x1,f(x1)) and Q(x2,f(x2)) Figure . In
geometry, a line joining two points of a curve is a secant to the
curve. Thus, the average rate of change of ƒ from x1 to x2 is
identical with the slope of secant PQ.
Experimental biologists often want to know the rates at which
populations grow undercontrolled laboratory conditions

14. EXAMPLE 2;
The Average Growth Rate of a Laboratory Population
Figure 2.2 shows how a population of fruit flies (Drosophila) grew in a
50-day experiment. The number of flies was counted at regular
intervals, the counted values plotted with respect to time, and the
points joined by a smooth curve (colored blue in Figure 2.2). Find the
average growth rate from day 23 to day 45.
Solution; There were 150 flies on day 23 and 340 flies on day 45.
Thus the number of flies increased by340-150=190 in 45-23=22 days.
The average rate of changeof the population from day 23 to day45was
Average rate of change:

15. Growth of a fruit fly population in a controlled experiment. The
average rate of change over 22 days is the slope∆p/∆t of the secant
line.
The average rate of change from day 23 to day 45 calculated in
Example 3 does nottell us how fast the population was changing on
day 23 itself. For that we need to examinetime intervals closer to
the day in question.

16. EXAMPLE 4;
The Growth Rate on Day 23 How fast was the number
of flies in the population of Example 3 growing on day
23?
Solution; To answer this question, we examine the
average rates of change over increasingly short time
intervals starting at day 23. In geometric terms, we find
these rates by calculating the slopes of secants from P
to Q, for a sequence of points Q approaching P along
the curve (Figure 2.3)

18. The values in the table show that the secant slopes rise from 8.6
to 16.4 as the t-coordinate of Q decreases from 45 to 30, and we
would expect the slopes to rise slightly higheras t continued on
toward 23. Geometrically, the secants rotate about P and seem
to approach the red line in the figure, a line that goes through P
in the same direction that thecurve goes through P. We will see
that this line is called the tangent to the curve at P.Since the line
appears to pass through the points (14, 0) and (35, 350),
it has slope
On day 23 the population was increasing at a rate of about 16.7 flies day.

19. Conclusion;
The rates at which the rock in Example 2 was falling at the instants
t=1 and t=2 and the rate at which the population in Example 4 was
changing on day t=23 are called instantaneous rates ofchange.
As the examples suggest, we find instantaneous rates aslimiting values of
average rates. In Example 4, we also pictured the tangent line to the
population curve on day 23 as a limiting position of secant lines.
Instantaneous rates and tangent lines, intimately connected, appear in
many other contexts.
To talk about the two constructively, and to understand the connection
further, we need to investigate the process by which we determine limiting
values, or limits, as we will soon call them.

20. Limits of Function Values
Our examples have suggested the limit idea. Let’s
begin with an informal definition oflimit, postponing
the precise definition until we’ve gained more
insight.
Let ƒ(x) be defined on an open interval about except
possibly at itself. If ƒ(x) gets arbitrarily close to L
(as close to L as we like) for all x sufficiently close
to we saythat ƒ approaches the limit L as x
approaches and we write
which is read “the limit of ƒ(x) as x approaches is L”. Essentially, the
definition says thatthe values of ƒ(x) are close to the number L
whenever x is close to (on either side of )

21. Limit
We say that the limit of ( ) as approaches is and write
f x x a L
lim ( )
x a
f x L


if the values of ( ) approach as approaches .
f x L x a
a
L
( )
y f x


22. Behavior of a Function Near a Point
How does the function behave near x=1?

23. Example 1(a):
f(x) = 2x – 1, Discuss the behavior of of f(x) when x gets closer
to 2 using graph
• Graph f(x) = 2x - 1
• When x is closer and
closer to 2,
F(x) is closer to 3
Therefore:
The limit of f(x) as x
approaches 2 is 3
lim(2x-1) = 3 = f(2)
X2

24. Example 1(b): f(x) = 2x - 1
Discuss the behavior of the values of f(x) when x gets
closer to 2 using table

25. Excercise
• Find: lim (x+2) and lim (3x+1)
X0 X -1
Do you get 2 and -2? If not, try again

26. Example 2:
Discuss the behavior of f(x) when x gets closer to 2
2
4
)
(
2



x
x
x
f
x 1.5 1.9 1.99 1.999 2 2.001 2.01 2.1 2.5
f (x) 3.5 3.9 3.99 3.999 ? 4.001 4.01 4.1 4.5
If x = 2, f(x) is undefined. If you graph, you will see a hole
there.
Therefore, when x is closer and closer to 2, f(x) is closer to 4
lim f(x) = 4 = f(2) or
X2

27. Example 2:
Discuss the behavior of the values of f(x) when x is closer to 2.
Does the limit exist?
2
2
)
(



x
x
x
f
x 0 1 1.9 1.99 2 2.001 2.01 2.1 2.5
f (x) -1 -1 -1 -1 ? 1 1 1 1
* This function is not defined when x = 2.
* The limit does not exist because the limit on
the left and the limit on the right are not the
same.
Lim f(x) = -1 represents the limit on the left of 2
Lim f(x) = 1 represents the limit on the right of 2
X2 -
X2 +

28. ■ We write
and call K the limit from the left (or left-hand limit) if
f (x) is close to K whenever x is close to c, but to the left
of c on the real number line.
■ We write
and call L the limit from the right (or right-hand limit) if
f (x) is close to L whenever x is close to c, but to the right
of c on the real number line.
■ In order for a limit to exist, the limit from the left and
the limit from the right must exist and be equal.

29. Example 3
(A) Discuss the behavior of
f(x) for x near 0
Lim f(x) =
Lim f(x) =
Lim f(x) =
F(0) =
X0 -
X 0 +
X0
0
0
0
0

30. (B) Discuss the behavior of
f(x) for x near 1
Lim f(x) =
Lim f(x) =
Lim f(x) =
F(1) =
X1 -
X 1 +
X1
Example 3 - continue
1
2
does not exist
not defined

31. (C) Discuss the behavior of
f(x) for x near 3
Lim f(x) =
Lim f(x) =
Lim f(x) =
F(3) =
X3 -
X 3 +
X3
Example 3 - continue
3
3
3
not defined

33. Lim (x2 + 5x)
= lim x2 + lim 5x
= (lim x) (lim x) + 5 (lim x)
= (-2) (-2) + 5 (-2)
= 4 – 10 = -6
X-2
Example 4
X-2 X-2
X-2 X-2 X-2
Property 1
Property 4 and 3
Try lim (x4 + 3x – 2)
X-1 If you don’t get -4, try again

34. Example 5
Lim
=
=
6
3 2

x
X2
X2
Property 8
Try lim
X-1
)
6
3
lim( 2

x
6
6
12
6
)
2
)(
2
(
3 



2
2 2

x If you don’t get 2, try again

35. Example 6
1
lim 2
2
2 

 x
x
x
)
1
(
lim
lim
2
2
2
2





x
x
x
x
5
4
1
)
2
)(
2
(
)
2
)(
2
(






Note that this is a
rational function with a
nonzero denominator at
x = -2
= =
2
lim 4
1 
 x
x
Try
x If you don’t get 1/3, try again

36. Example 7







12
3
2
)
(
x
x
x
f
If x < 5
If x > 5
A)Lim f(x) =
lim (2x+3) = 2(5)+ 3 = 13
X5-
X5-
B) Lim f(x) =
lim (-x+12)=-5+12=7
X5+
X5+
C) Lim f(x) =
Does not exist because the left hand the right hand limits are not equal
X5
D) F(5) =
is not defined

38. Example 8:
Use algebraic and/or graphical techniques to
analyze each of the following indeterminate forms
2
2
1
2
2
1
2
1
)
1
(
1
lim
1
)
1
(
lim
1
1
lim









x
x
x
x
x
x
x
x
x
A)
C)
B)
See next page for step by
step instruction

39. Example 8 - Solutions
Note: when you find the limits of the above problems, you must factor first
and then simplify before you substitute the number for x

40. Different Quotient (pre-cal)
h
x
f
h
x
f )
(
)
( 

Indeterminate form

41. Examples:
• Find the following limit for the following functions
h
f
h
f
x
x
f
h
f
h
f
x
x
f
h
f
h
f
x
x
f
h
h
h
)
3
(
)
3
(
lim
;
)
(
)
1
(
)
1
(
lim
;
1
)
(
)
4
(
)
4
(
lim
;
2
7
)
(
0
0
0














9)
10)
11)
See the next pages for step by step instruction

43. Because the limit on the left and the litmit
on the right are not the same.
Therefore, this limit does not exist

44. Rationalize the numerator

45. Home work
• Exercise 1.3
• Q # 1 Part iii, iv and v
• Q # 2 Part iv, vi and ix

46. THANK YOU