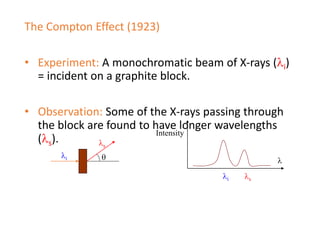
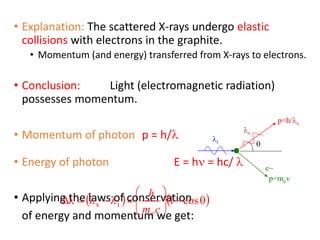
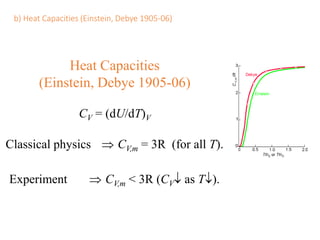
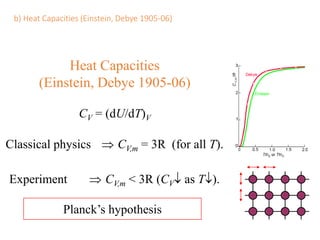
The document discusses several experiments from 1905-1925 that provided evidence that challenged classical physics and led to the development of quantum theory, including: - Heat capacity experiments showing heat capacity decreases with temperature, contradicting classical physics (1905-1906) - Photoelectric effect experiments showing electrons ejected by frequency-dependent photons, not intensity (1905) - 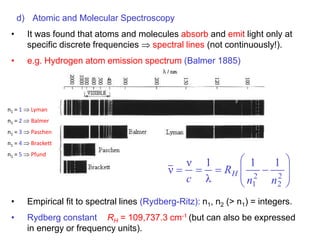Atomic spectroscopy experiments showing atoms absorb/emit only discrete frequencies (1885, early 1900s)

2. Heat Capacities
(Einstein, Debye 1905-06)

3. • Heat capacity – relates rise in energy of a material
with its rise in temperature:
CV = (dU/dT)V
Heat Capacities
(Einstein, Debye 1905-06)

4. b) Heat Capacities (Einstein, Debye 1905-06)
Classical physics  CV,m = 3R (for all T).
Heat Capacities
(Einstein, Debye 1905-06)
CV = (dU/dT)V

5. b) Heat Capacities (Einstein, Debye 1905-06)
Classical physics  CV,m = 3R (for all T).
Heat Capacities
(Einstein, Debye 1905-06)
CV = (dU/dT)V
Experiment  CV,m < 3R (CV as T).

6. b) Heat Capacities (Einstein, Debye 1905-06)
Classical physics  CV,m = 3R (for all T).
Heat Capacities
(Einstein, Debye 1905-06)
CV = (dU/dT)V
Experiment  CV,m < 3R (CV as T).

7. b) Heat Capacities (Einstein, Debye 1905-06)
Classical physics  CV,m = 3R (for all T).
Heat Capacities
(Einstein, Debye 1905-06)
CV = (dU/dT)V
Experiment  CV,m < 3R (CV as T).
Planck’s hypothesis

8. Conclusion
vibrational energy in solids is quantized:
vibrational frequencies of solids can only
have certain values ()
vibrational energy can only change by
integer multiples of h.

9. c) Photoelectric Effect (Einstein 1905)
• Ideas of Planck applied to electromagnetic radiation.
• No electrons are ejected (regardless of light intensity) unless 
exceeds a threshold value characteristic of the metal.
• Ek independent of light intensity but linearly dependent on .
• Even if light intensity is low, electrons are ejected if  is above the
threshold. (Number of electrons ejected increases with light
intensity).
• Conclusion: Light consists of discrete packets (quanta) of
energy = photons (Lewis, 1922).
e
P
h
o
t
e
l
e
c
t
r
o
n
s
-
h
Metal surface
work function = F
e
Photoelectrons ejected with
kinetic energy:
Ek = h - F

10. d) Atomic and Molecular Spectroscopy
• It was found that atoms and molecules absorb and emit light only at
specific discrete frequencies spectral lines (not continuously!).
• e.g. Hydrogen atom emission spectrum (Balmer 1885)
• Empirical fit to spectral lines (Rydberg-Ritz): n1, n2 (> n1) = integers.
• Rydberg constant RH = 109,737.3 cm-1 (but can also be expressed
in energy or frequency units).











 2
2
2
1
1
1
λ
1
ν
ν
n
n
R
c
H
n1 = 1  Lyman
n1 = 2  Balmer
n1 = 3  Paschen
n1 = 4  Brackett
n1 = 5  Pfund

11. The Compton Effect (1923)
• Experiment: A monochromatic beam of X-rays (i)
= incident on a graphite block.
• Observation: Some of the X-rays passing through
the block are found to have longer wavelengths
(s).

i
s
Intensity

i s

12. • Explanation: The scattered X-rays undergo elastic
collisions with electrons in the graphite.
• Momentum (and energy) transferred from X-rays to electrons.
• Conclusion: Light (electromagnetic radiation)
possesses momentum.
• Momentum of photon p = h/
• Energy of photon E = h = hc/ 
• Applying the laws of conservation
of energy and momentum we get:
i
s

e
p=h/s
p=mev
   












 cos
1
λ
λ
Δλ i
s
c
m
h
e

13. Particles Behaving as Waves
Electron Diffraction (Davisson and Germer, 1925)
Davisson and Germer showed that
a beam of electrons could be diffracted
from the surface of a nickel crystal.
Diffraction is a wave property – arises
due to interference between scattered waves.
This forms the basis of electron diffraction – an
analytical technique for determining the
structures of molecules, solids and surfaces (e.g.
LEED).
NB: Other “particles” (e.g. neutrons,
protons, He atoms) can also be
diffracted by crystals.