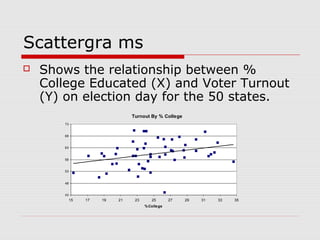
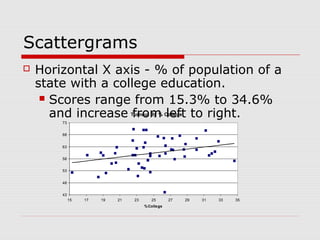
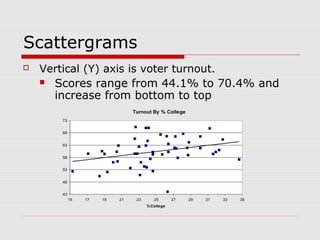
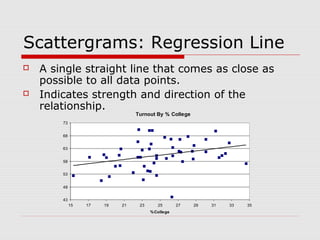
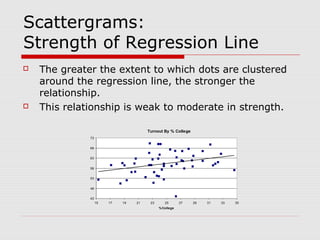
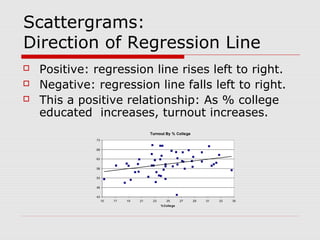
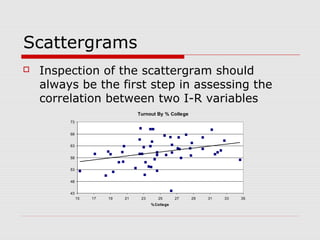
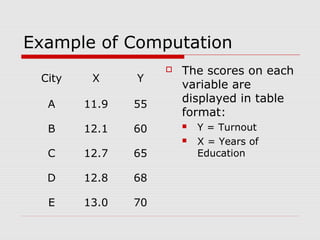
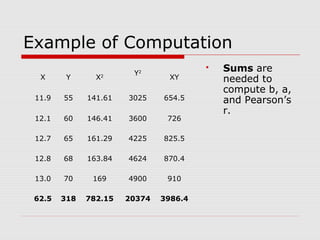
This document discusses the relationship between variables measured at the interval-ratio level. It provides examples of how to interpret scattergrams and the regression line to assess the strength and direction of relationships between two variables. It also explains how to calculate Pearson's correlation coefficient r and how r values between 0 and 1 indicate the strength of association between variables. r values closer to 1 represent stronger relationships.

1. Chapter 15
Association Between Variables
Measured at the Interval-Ratio
Level

2. Chapter Outline
 Interpreting the Correlation
Coefficient: r 2
 The Correlation Matrix
 Testing Pearson’s r for Significance
 Interpreting Statistics: The Correlates
of Crime

3. Scattergrams
 Scattergrams have two dimensions:
 The X (independent) variable is arrayed
along the horizontal axis.
 The Y (dependent) variable is arrayed
along the vertical axis.

4. Scattergrams
 Each dot on a scattergram is a case.
 The dot is placed at the intersection
of the case’s scores on X and Y.

5. Scattergra ms
 Shows the relationship between %
College Educated (X) and Voter Turnout
(Y) on election day for the 50 states.
Turnout By % College
73
68
63
58
53
48
43
15 17 19 21 23 25 27 29 31 33 35
% College

6. Scattergrams
 Horizontal X axis - % of population of a
state with a college education.
 Scores range from 15.3% to 34.6%
and increase from left to right.
Turnout By % College
73
68
63
58
53
48
43
15 17 19 21 23 25 27 29 31 33 35
% College

7. Scattergrams
 Vertical (Y) axis is voter turnout.
 Scores range from 44.1% to 70.4% and
increase from bottom to top
Turnout By % College
73
68
63
58
53
48
43
15 17 19 21 23 25 27 29 31 33 35
% College

8. Scattergrams: Regression Line
 A single straight line that comes as close as
possible to all data points.
 Indicates strength and direction of the
relationship.
Turnout By % College
73
68
63
58
53
48
43
15 17 19 21 23 25 27 29 31 33 35
% College

9. Scattergrams:
Strength of Regression Line
 The greater the extent to which dots are clustered
around the regression line, the stronger the
relationship.
 This relationship is weak to moderate in strength.
Turnout By % College
73
68
63
58
53
48
43
15 17 19 21 23 25 27 29 31 33 35
% College

10. Scattergrams:
Direction of Regression Line
 Positive: regression line rises left to right.
 Negative: regression line falls left to right.
 This a positive relationship: As % college
educated increases, turnout increases.
Turnout By % College
73
68
63
58
53
48
43
15 17 19 21 23 25 27 29 31 33 35
% College

11. Scattergrams
 Inspection of the scattergram should
always be the first step in assessing the
correlation between two I-R variables
Turnout By % College
73
68
63
58
53
48
43
15 17 19 21 23 25 27 29 31 33 35
% College

12. The Regression Line: Formula
 This formula defines the regression line:
 Y = a + bX
 Where:
 Y = score on the dependent variable
 a = the Y intercept or the point where the
regression line crosses the Y axis.
 b = the slope of the regression line or the
amount of change produced in Y by a unit
change in X
 X = score on the independent variable

13. Regression Analysis
 Before using the formula for the regression line, a
and b must be calculated.
 Compute b first, using Formula 15.3 (we won’t do
any calculation for this chapter)

14. Regression Analysis
 The Y intercept (a) is computed from
Formula 15.4:

15. Regression Analysis
 For the relationship between % college
educated and turnout:
 b (slope) = .42
 a (Y intercept)= 50.03
 Regression formula: Y = 50.03 + .42 X
 A slope of .42 means that turnout increases
by .42 (less than half a percent) for every
unit increase of 1 in % college educated.
 The Y intercept means that the regression
line crosses the Y axis at Y = 50.03.

16. Predicting Y
 What turnout would be expected in a state
where only 10% of the population was
college educated?
 What turnout would be expected in a state
where 70% of the population was college
educated?
 This is a positive relationship so the value
for Y increases as X increases:
 For X =10, Y = 50.3 +.42(10) = 54.5
 For X =70, Y = 50.3 + .42(70) = 79.7

17. Pearson correlation coefficient
 But of course, this is just an estimate of
turnout based on % college educated, and
many other factors also affect voter
turnout.
 How much of the variation in voter turnout
depends on % college educated? The
relevant statististic is the coefficient of
determination (r squared), but first we
need to learn about Pearson’s correlation
coefficient (r).

18. Pearson’s r
 Pearson’s r is a measure of association for I-R
variables.
 It varies from -1.0 to +1.0
 Relationship may be positive (as X increases, Y
increases) or negative (as X increases, Y decreases)
 For the relationship between % college educated and
turnout, r =.32.
 The relationship is positive: as level of education
increases, turnout increases.
 How strong is the relationship? For that we use R
squared, but first, let’s look at the calculation process

19. Example of Computation
 The computation and interpretation of a, b,
and Pearson’s r will be illustrated using
Problem 15.1.
 The variables are:
 Voter turnout (Y)
 Average years of school (X)
 The sample is 5 cities.
 This is only to simplify computations, 5 is much
too small a sample for serious research.

20. Example of Computation
 The scores on each
City X Y
variable are
A 11.9 55
displayed in table
format:
B 12.1 60  Y = Turnout
 X = Years of
C 12.7 65 Education
D 12.8 68
E 13.0 70

21. Example of Computation
Y2
 Sums are
X Y X2
XY needed to
compute b, a,
11.9 55 141.61 3025 654.5 and Pearson’s
r.
12.1 60 146.41 3600 726
12.7 65 161.29 4225 825.5
12.8 68 163.84 4624 870.4
13.0 70 169 4900 910
62.5 318 782.15 20374 3986.4

22. Interpreting Pearson’s r
 An r of 0.98 indicates an extremely strong
relationship between average years of
education and voter turnout for these five
cities.
 The coefficient of determination is r2 = .96.
Knowing education level improves our
prediction of voter turnout by 96%. This is
a PRE measure (like lambda and gamma)
 We could also say that education explains
96% of the variation in voter turnout.

23. Interpreting Pearson’s r
 Our first example provides a more
realistic value for r.
 The r between turnout and % college
educated for the 50 states was:
 r = .32
 This is a weak to moderate, positive
relationship.
 The value of r2 is .10.
Percent college educated explains
10% of the variation in turnout.