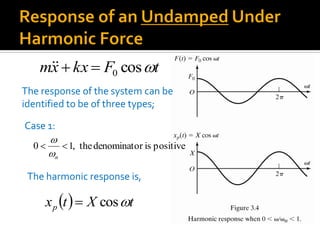
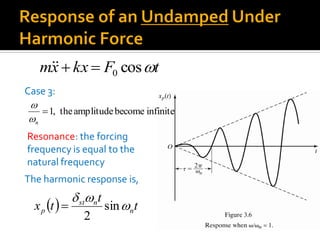
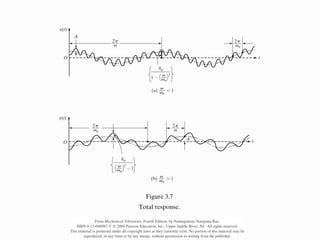
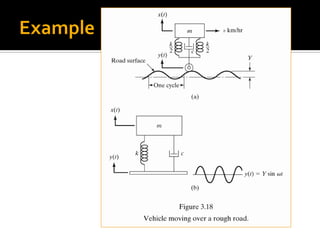
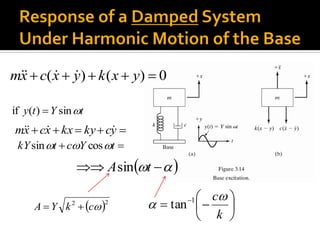
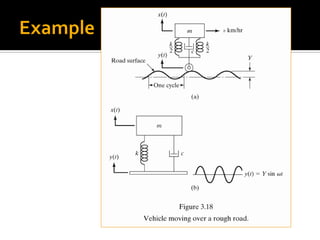
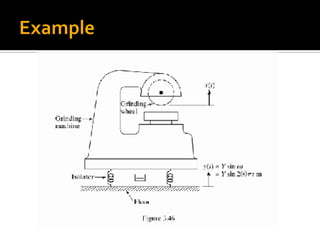
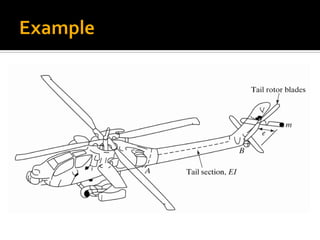
This chapter discusses forced vibration in mechanical systems. It defines forced vibration as when external energy is supplied to a system during vibration through an applied force or imposed displacement. The excitation can be harmonic, periodic but nonharmonic, nonperiodic, or random. Harmonic response and transient response are examined for a single degree of freedom system under harmonic excitation. Resonance is discussed, where the forcing frequency equals the natural frequency, causing infinite amplitude. The response of such a system is derived. Characteristics of the magnification factor and phase angle are also summarized.

1. Chapter 3

2.  A mechanical system is said to undergo
forced vibration whenever external energy is
supplied to the system during vibration
 External energy can be supplied to the
system through either an applied force or an
impose displacement excitation
 The applied force or displacement may be
harmonic, nonharmonic but periodic,
nonperiodic, or random

3.  Harmonic or transient responses
 Dynamic response of a single degree of
freedom under harmonic excitations
 Resonance
 Examples: unbalanced rotating response, the
oscillation of a tall chimney due to vortex
shedding and the vertical motion of an
automobile on a sinusoidal road surface

4.  tFkxxcxm  
0 kxxcxm 
Homogenous solution;
The solution;
  2chaptertxh 
This free vibration dies out with time under each of the three possible
conditions of damping and under all possible initial conditions.

5.  tFkxxcxm  
•The general solution
eventually reduces to a
particular solution xp (t), which
represents the steady-state
vibration
•The steady-state motion is
present as long as the forcing
function
  .....txp
Particular solution;

7. tFkxxm cos0
•The maximum amplitude of xp (t);
  tCtCtx nnh  sincos 21 
The homogeneous solution;
The particular solution;
  tXtxp cos
22
0
1 









n
st
mk
F
X





8. tFkxxm cos0
Using the initial conditions x(t=0) = x0 and v(t=0)=v0
  t
mk
F
tCtCtx nnh 

 cossincos 2
0
21


The total solution is;
2
0
01
mk
F
xC


n
x
C

0
2



9. tFkxxm cos0
2
1
1








n
st
X


The maximum amplitude can be
expressed;
Magnification factor, amplitude ratio
Frequency ratio, r

10. tFkxxm cos0
The response of the system can be
identified to be of three types;
Case 1:
positiveisrdenominatothe,10 
n

  tXtxp cos
The harmonic response is,

11. tFkxxm cos0
Case 2:
negativeisrdenominatothe,1
n

  tXtxp cos
The harmonic response is,
1
2







n
st
X




12. tFkxxm cos0
Case 3:
infinitebecomeamplitudethe,1
n

  t
t
tx n
nst
p 

sin
2

The harmonic response is,
Resonance: the forcing
frequency is equal to the
natural frequency

13. tFkxxm cos0
  t
t
t
x
txtx n
nst
n
n
n 



 sin
2
sincos 0
0 

The response of the system at resonance becomes;

14. tFkxxm cos0
The total response of the system can also be expressed
  1;cos
1
cos)( 2









n
n
st
n forttAtx







  1;cos
1
cos)( 2









n
n
st
n forttAtx








16.  A weight of 50 N is suspended from a spring
of stiffness 4000 N/m and is subjected to a
harmonic force of amplitude 60 N and
frequency 6 Hz. Find (a) the extension of the
spring due to the suspended weight, (b) the
static displacement of the spring due to the
maximum applied force, and the amplitude of
forced motion of the weight

17.  Consider a spring –mass system, with k=4000
N/m and mass, m=10 kg, subject to a
harmonic force F(t) = 400 cos 10 t N. Find the
total response of the system under the
following initial condition;
 x0 = 0.1m, v0 = 0

18.  The spring actuator shown in the figure operates
by using air pressure from a pneumatic
controller (p) as input and providing an output
displacement to a valve (x) proportional to the
input air pressure.The diaphragm, made of a
fabric-base rubber, has an area A and deflects
under the input air pressure against a spring of
stiffness k. Find the response of the valve under
a harmonically fluctuating input air pressure
p(t)=p0 sinωt for the following data:
 p0=10 psi, ω=8 rad/s, A=10 in2, k=400 lb/in, weight of
spring = 15 lb, and weight of valve and valve rod = 20
lb.

20. tFkxxcxm cos0 
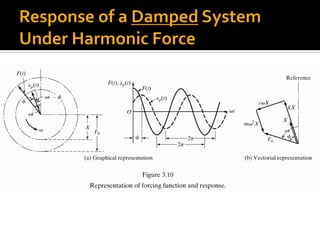
  tFtF cos0
The particular solution;
   tXtxp cos)(
  2/12222
0
][  cmk
F
X









 
2
1
tan



mk
c

22. Dividing X by k and substituting;
m
k
n 
mk
c
m
c
c
c
nc 22


 n
m
c
2
n
r



k
F
st
0

   222
2/1
2
2
2
21
1
21
1
rr
X
n
st 





 





























































 
2
1
2
1
1
2
tan
1
2
tan
r
r
n
n 







24.  Some characteristics of the magnification
factor;
 Any amount of damping reduces the
magnification factor
 For any specified value of r, a higher value of
damping reduces the value of M
 In the degenerate case of a constant force (r=0),
the value of M=1
 The reduction in M in the presence of damping is
very significant at or near resonance

25.  The amplitude of the forced vibration becomes
smaller with increasing values of the forcing
frequency ( that is M→0 as r → ∞)
 For 0 ≤ ζ≤ 1/√2, the maximum value of M occurs
when
 The maximum value of X is
22
21or21   nr
2
max 12
1
 






st
X
 
2
1






 n
st
X

26.  For ζ= 1/√2, dM/dr =0 when r=0.
 For ζ> 1/√2, the graph of M monotonically
decrease with increasing r

27.  Some characteristics of the phase angle;
 For an undamped system (ζ=0), the phase angle is
0 for 0< r < 1 and 180° for r > 1.This implies that
the excitation and the response are in phase for
0 < r < 1 and out phase for r > 1
 For ζ > 1 and 0 < r < 1, the phase angle is given by
0 < φ < 90°, implying that the response lags the
excitation
 For ζ > 0 and r > 1, the phase angle is given by
90° < φ < 180°, implying that response leads the
excitation

28.  For ζ > 0 and r = 1, the
phase angle is given by
φ = 90°, implying that
the phase difference
between the excitation
and the response is 90°
 For ζ > 1 and large
values of r, the phase
angle approaches 180° ,
implying that the
response and excitation
are out of phase

29. The complete solution, for an underdamped system,
     
 
tXteXtx d
tn
coscos 00


sincoscos
coscos
000
000
XXXx
XXx
dn 


For the initial condition,     00 0and0 xtxxtx  
     2/12
00
2
000 sincos  XXX 
00
00
0
cos
sin
tan



X
X

   222
21 rr
X st











 
2
1
1
2
tan
r
r


30.  For a vibrating system, m = 10 kg, k = 2500
N/m, and c = 45 N-s/m. A harmonic force 180
N and frequency 3.5 Hz acts on the mass. If
the initial displacement and velocity of the
mass are 15mm and 5 m/s, find the complete
solution representing the motion of the mass.

31. Q
XX
n
stsmallst













 
2
1
The quality factor, Q, is the value of
the of the amplitude ratio at
resonance.
For small values of damping, (ζ<0.05),
The points R1 and R2, where the amplification
factor falls to Q/√2, are called half power
points because the power absorbed by the
damper is proportional to the square of the
amplitude: 2
XcW 

32. 122
1


 
 n
Q
The difference between the frequencies
associated with the half power points is
called bandwidth



21
2
12
1
2
1 






n
rR 


21
2
22
2
2
2 






n
rR
n 212 

33. The harmonic forcing function can be represented
in complex form as F(t)=F0eiωt
ti
Fekxxcxm 
 
Assuming the particular solution;
  ti
p Xetx 

  


 icmk
F
X 2
0







 
2
1
tan



mk
c
  


i
e
cmk
F
X 

 2/1
2222
0

34. The steady-state solution;
The Frequency Response,
  


 icmk
F
X 2
0
  responsefrequencycomplexiH
 
  
 



 ti
p e
cmk
F
tx 2/1
2222
0
 

iH
rirF
kX



21
1
2
0

35. The Frequency Response,
 
     2/1
222
0 21
1
rrF
kX
iH



The absolute value ,
     
 
 ti
p eiH
k
F
tx 0
     
)(velocity 0
txieiH
k
F
itx p
ti
p  
 

       
)(accel. 202
txeiH
k
F
itx p
ti
p  
 


36.  The figure shows a simple model of a motor
vehicle that can vibrate in the vertical direction
while traveling over a rough road.The vehicle
has a mass of 1200 kg.The suspension system
has a spring constant of 400 kN/m and a
damping ratio of 0.5. If the vehicle speed is 20
km/hr, determine the displacement amplitude of
the vehicle.The road surface varies sinusoidally
with an amplitude ofY = 0.05 m and a
wavelength of 6m.

38. 0)()(  yxkyxcxm 
 yckykxxcxm 
 22
ckYA  





 
k
c
 1
tan
tYty sin)(if 
 tYctkY  cossin
   tAsin

39.  
   
 





 12/1222
22
sin
][
)( t
cmk
ckY
txp







 
2
1
1 tan



mk
c
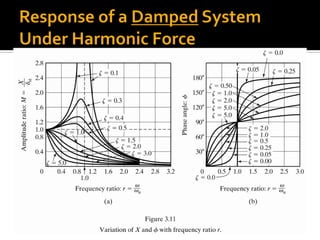
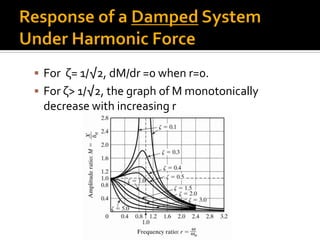
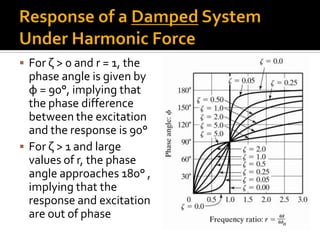
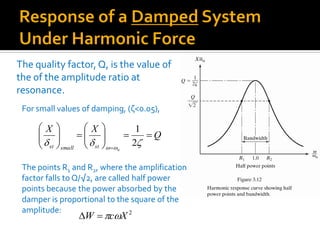
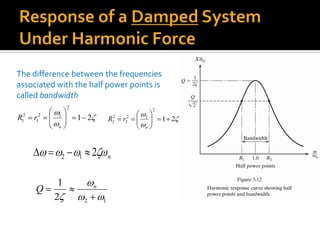
The steady state response of the mass,






 
k
c
 1
tan

40.    tAtxp sin)(
The response can be rewritten as,
 
   
 
   
2/1
222
22
1
222
22
21
21






















rr
r
cmk
ck
Y
X




      













 
22
3
1
22
3
1
141
2
tantan
r
r
cmkk
mc





Displacement transmissibility,

42. 













 ti
p Ye
rir
ri
tx 


21
21
Re)( 2
     iHrT
Y
X
d
2/12
21
The harmonic excitation of the base expressed in complex
form as
)Re()( ti
Yety 

The response of the system ,

43.  Some characteristics of the displacement
transmissibility;
 The value ofTd is unity at r=0 and close to unity for
small value of r
 For an undamped system (ζ=0),Td →∞ at
resonance (r=1)
 The value ofTd is less than unity for values r > √2
 The value ofTd =1 for all values of ζ at r= √2
 For r< √2, smaller damping ratio lead to larger
values ofTd .

44.  Some characteristics of the displacement
transmissibility;
 For r> √2, smaller damping ratio lead to smaller
values ofTd
 Td attains a maximum for 0<ζ<1 at the frequency
ratio r = rm < 1;
  2/1
2
181
2
1
 

mr

45.     xmyxcyxkF  
A force is transmitted to the base
or support due to the reaction from
the spring and the dashpot,
 
   
2/1
222
2
2
21
21











rr
r
r
kY
FT


Force transmissibility,
     tFtXmF T sinsin2

46.  
   
2/1
222
2
2
21
21











rr
r
r
kY
FT


Force transmissibility,

47. Relative Motion, z = x – y,
tYmymkzzcxm  sin2
 
   
    
 1
2/1
222
2
sin
sin







tZ
cmk
tYm
tz

48. Relative Motion, z = x – y,
       222
2
222
2
21 rr
r
Y
cmk
Ym
Z




















 
2
1
2
1
1
1
2
tantan
r
r
mk
c 




49.  The figure shows a simple model of a motor
vehicle that can vibrate in the vertical direction
while traveling over a rough road.The vehicle
has a mass of 1200 kg.The suspension system
has a spring constant of 400 kN/m and a
damping ratio of 0.5. If the vehicle speed is 20
km/hr, determine the displacement amplitude of
the vehicle.The road surface varies sinusoidally
with an amplitude ofY = 0.05 m and a
wavelength of 6m.

51.  A heavy machine, weighing 3000 N supported
on a resilient foundation.The static deflection of
the foundation due to the weight of the machine
is found to be 7.5 cm. It is observed that the
machine vibrates with an amplitude of 1 cm
when the base of the foundation is subjected to
harmonic oscillation at the undamped natural
frequency of the system with an amplitude of
0.25 cm. Find (a) the damping constant of the
foundation, (b) the dynamic force amplitude on
the base, and (c) the amplitude of the of the
machine relative to the base.

52.  A precision grinding machine is supported on an
isolator that has a stiffness of 1 MN/m and a
viscous damping constant of 1 kN-s/m.The floor
on which the machine is mounted is subjected to
a harmonic disturbance due to the operation of
an unbalanced engine in the vicinity of the
grinding machine. Find the maximum
acceptable displacement amplitude of the floor
if the resulting amplitude of vibration of the
grinding wheel is to be restricted to 10-6 m.
Assume that the grinding machine and the
wheel are a rigid body of weight 5000 N

54.  One of the tail rotor blades of a helicopter has
an unbalanced mass of m=0.5 kg at a distance
of e = 0.15 m from the axis of rotation , as
shown in the figure.The tail section has a
length of 4 m, a mass of 240 kg, a flexural
stiffness (EI) of 2.5 MN – m2 , and a damping
ratio of 0.15.The mass of the tail rotor blades,
including their drive system, is 20 kg.
Determine the forced response of the tail
section when the blades rotate at 1500 rpm

57. tmekxxcxM  sin2
 
  tmetF  sin2

The particular solution;
 
   





















ti
n
p
eiH
M
me
tXtx
2
Im
sin)(

58.  
 




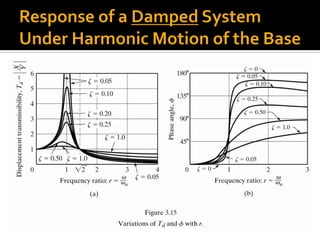
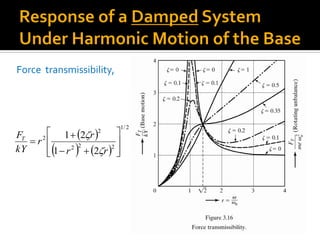
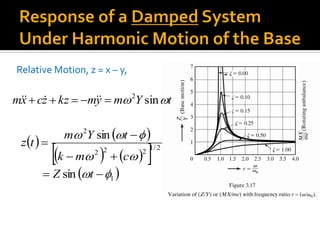
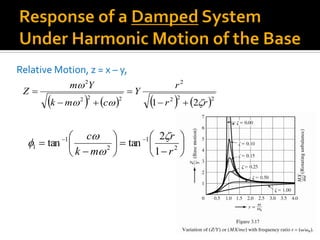
iH
M
me
cMk
me
X
n









2/12222
2
][







 
2
1
tan



Mk
c
      

iHr
rr
r
me
MX 2
222
2
21










 
2
1
1
2
tan
r
r


60.  The following observation can be made from
the equations;
 All the curves begin at zero amplitude.The
amplitude near resonance is markedly affected by
damping.Thus if the machine is to be run near
resonance, damping should be introduced
purposefully to avoid dangerous amplitudes.
 At very high speeds(ω large), MX/me is almost
unity, and the effect of damping is negligible.

61.  The following observation can be made from
the equations;
 For 0 < ζ < 1 /√2, the maximum of MX/me is
▪ The peaks occur to the right of the resonance value r=1
 Forζ > 1 /√2, MX/me does not attain a maximum.
Its value grows from 0 at r=0 to 1 at r→∞.
2
max 12
1
 






me
MX