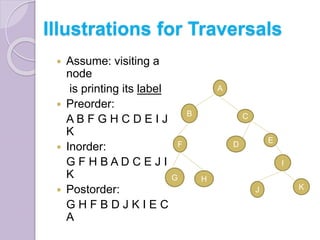
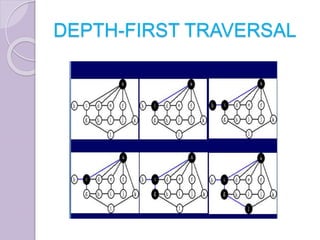
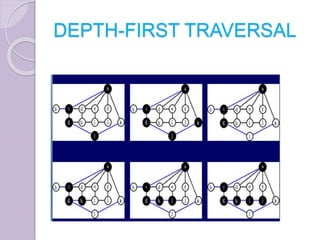
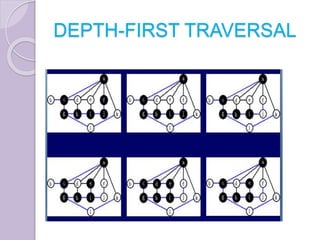
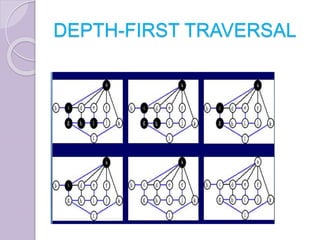
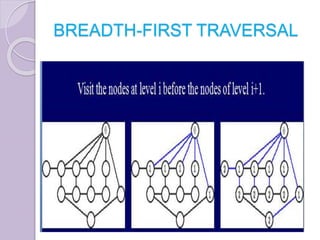
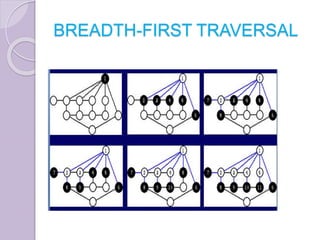
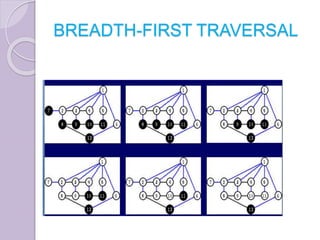
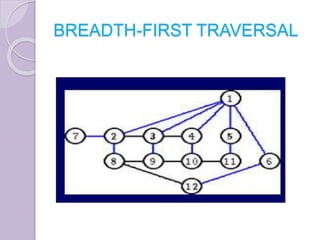
The document discusses binary tree traversal techniques, including preorder, inorder, and postorder methods, detailing their recursive algorithms. It also covers graph traversal methods, specifically depth-first and breadth-first traversals, explaining their differences and implementations. The algorithms provided demonstrate how to process nodes within each traversal method effectively.

1. NADARSARASWATHI COLLEGE OF ARTS
AND SCIENCE
DATA STRUCTURE ALOGIRTHM
TECHNIQUES FOR BINARY TREES
TECHNIQUES FOR GRAPHS
PRESENTED BY:
S.SABTHAMI
I.M.Sc(IT)

2. Binary Tree Traversal
Traversal is the process of visiting every node
once visiting a node entails doing some processing
at that node, but when describing a traversal
strategy

3. Binary Tree Traversal
Techniques
 Three recursive techniques for binary
tree traversal
 In each technique, the left subtree is
traversed recursively, the right subtree
is traversed recursively, and the root is
visited
 What distinguishes the techniques from
one another is the order of those 3
tasks

4. Preoder, Inorder, Postorder
 In Preorder, the root
is visited before (pre)
the subtrees traversals
 In Inorder, the root is
visited in-between left
and right subtree
traversal
 In Preorder, the root
is visited after (pre)
the subtrees traversals
 Preorder Traversal:
1. Visit the root
2. Traverse left subtree
3. Traverse right subtree
 Inorder Traversal:
1. Traverse left subtree
2. Visit the root
3. Traverse right subtree
 Postorder Traversal:
1. Traverse left subtree
2. Traverse right subtree
3. Visit the root

5. Illustrations for Traversals
 Assume: visiting a
node
is printing its label
 Preorder:
A B F G H C D E I J
K
 Inorder:
G F H B A D C E J I
K
 Postorder:
G H F B D J K I E C
A
A
B C
D
E
I
J K
F
G H

6. Code for the Traversal
Techniques
 The code for visitis up to you to provide,
depending
on the application
 A typical example for visit(…) is to print
out the data
part of its input node

7. ALGORITHM FOR PREORDER
void preOrder(Tree *tree){
if (tree->isEmpty( )) return;
visit(tree->getRoot( ));
preOrder(tree->getLeftSubtree());
preOrder(tree->getRightSubtree());
}

8. ALGORITHM FOR INORDER
void inOrder(Tree *tree){
if (tree->isEmpty( )) return;
inOrder(tree->getLeftSubtree( ));
visit(tree->getRoot( ));
inOrder(tree->getRightSubtree( ));
}

9. ALGORITHM FOR
POSTORDER
void PostOrder(struct Treenode*t)
{
if(t){
PostOrder(t->1child);
PostOrder(t->child);
Visit(t);
}
}

10. Graph Traversal
Depth-First Traversal
Breadth-First Traversal

11. Depth-First Traversal
 algorithm dft(x)
visit(x)
FOR each y such that (x,y) is an edge DO
IF <y was not visited yet >
THEN dft(y)

12. Depth-First Traversal
 A recursive algorithm implicitly
recording a “backtracking” path from
the root to the node currently under
consideration

13. DEPTH-FIRST TRAVERSAL
• Depth first search is another way
of traversing graphs, which is
closely related to preorder
traversal of a tree.
• the Breath-first search tree is typically
"short and bushy", the DFS tree is
typically "long and stringy".

14. DEPTH-FIRST TRAVERSAL

15. DEPTH-FIRST TRAVERSAL

16. DEPTH-FIRST TRAVERSAL

17. DEPTH-FIRST TRAVERSAL

18. BREADTH-FIRST TRAVERSAL
• Each vertex is clearly
• marked at most once,
• added to the list at most once (since that happens only
when it's marked), and
• removed from the list at most once.
◦ Since the time to process a vertex is proportional to the
length of its adjacency list, the total time for the whole
algorithm is O(m).
• A tree T constructed by the algorithm is called a breadth
first search tree.
• The traversal goes a level at a time, left to right within a
level (where a level is defined simply in terms of distance
from the root of the tree).

19. BREADTH-FIRST TRAVERSAL
• Every edge of G can be classified into one of three
groups.
• Some edges are in T themselves.
• Some connect two vertices at the same level of T.
• The remaining ones connect two vertices on two
adjacent levels. It is not possible for an edge to skip
a level.
• Breadth-first search tree really is a shortest path tree
starting from its root.

20. BREADTH-FIRST TRAVERSAL

21. BREADTH-FIRST TRAVERSAL

22. BREADTH-FIRST TRAVERSAL

23. BREADTH-FIRST TRAVERSAL

24. Relation between BFS and
DFS
 Both of these search algorithms now keep a list
of edges to explore; the only difference
between the two is
 while both algorithms adds items to the end of L,
• BFS removes them from the beginning, which
results in maintaining the list as a queue
• DFS removes them from the end, maintaining
the list as a stack.

25. BFS and DFS in directed
graphs
 The same search routines work essentially
unmodified for directed graphs.
◦ The only difference is that when exploring a
vertex v, we only want to look at edges (v,w)
going out of v; we ignore the other edges
coming into v.

26. BFS AND DFS IN DIRECTED
GRAPHS
 For BFS in directed graphs each edge of the
graph either
• connects two vertices at the same level
• goes down exactly one level
• goes up any number of levels.
 For DFS, each edge either connects an ancestor
to
• a descendant
• a descendant to an ancestor
• one node to a node in a previously visited
subtree.