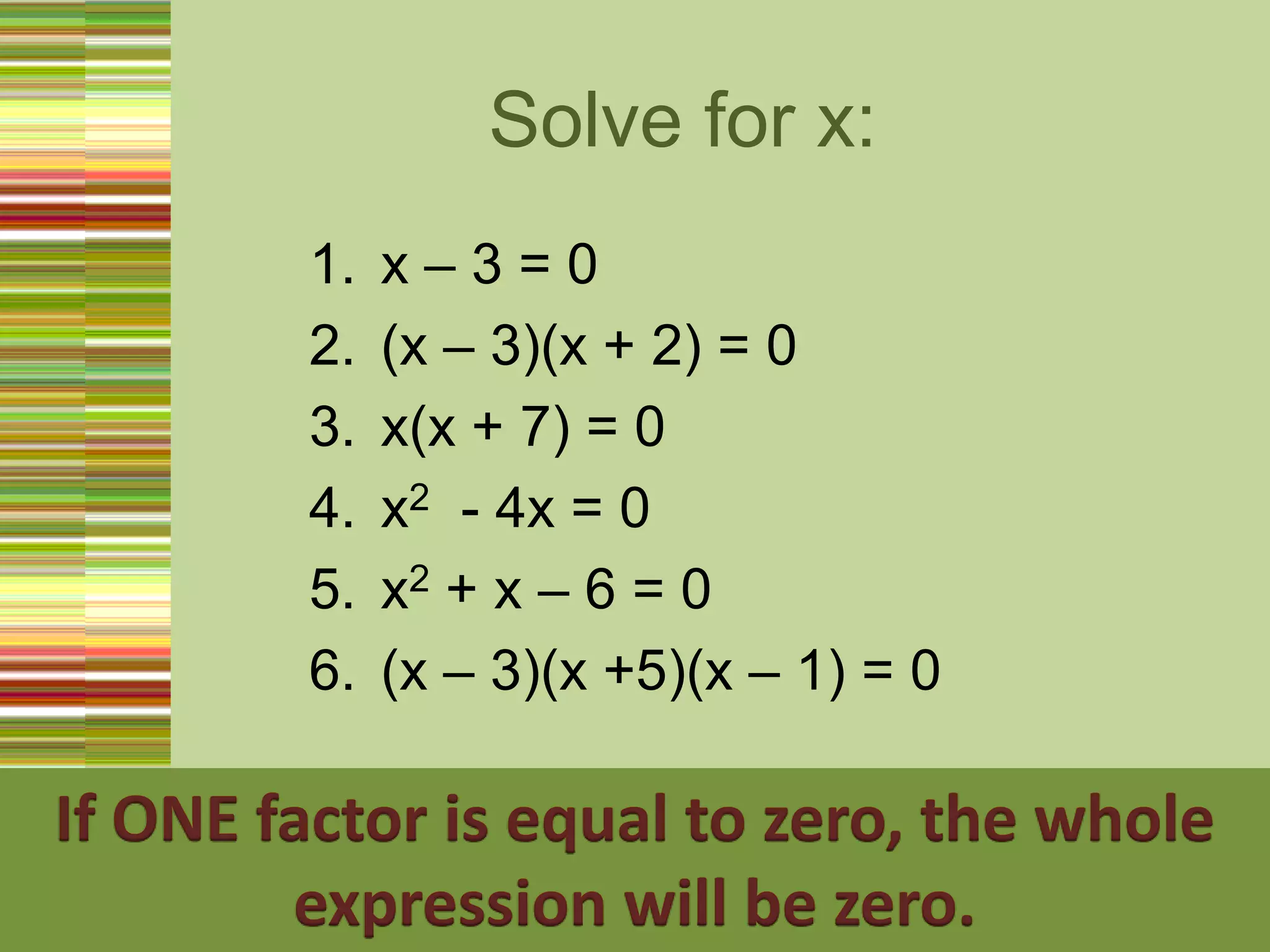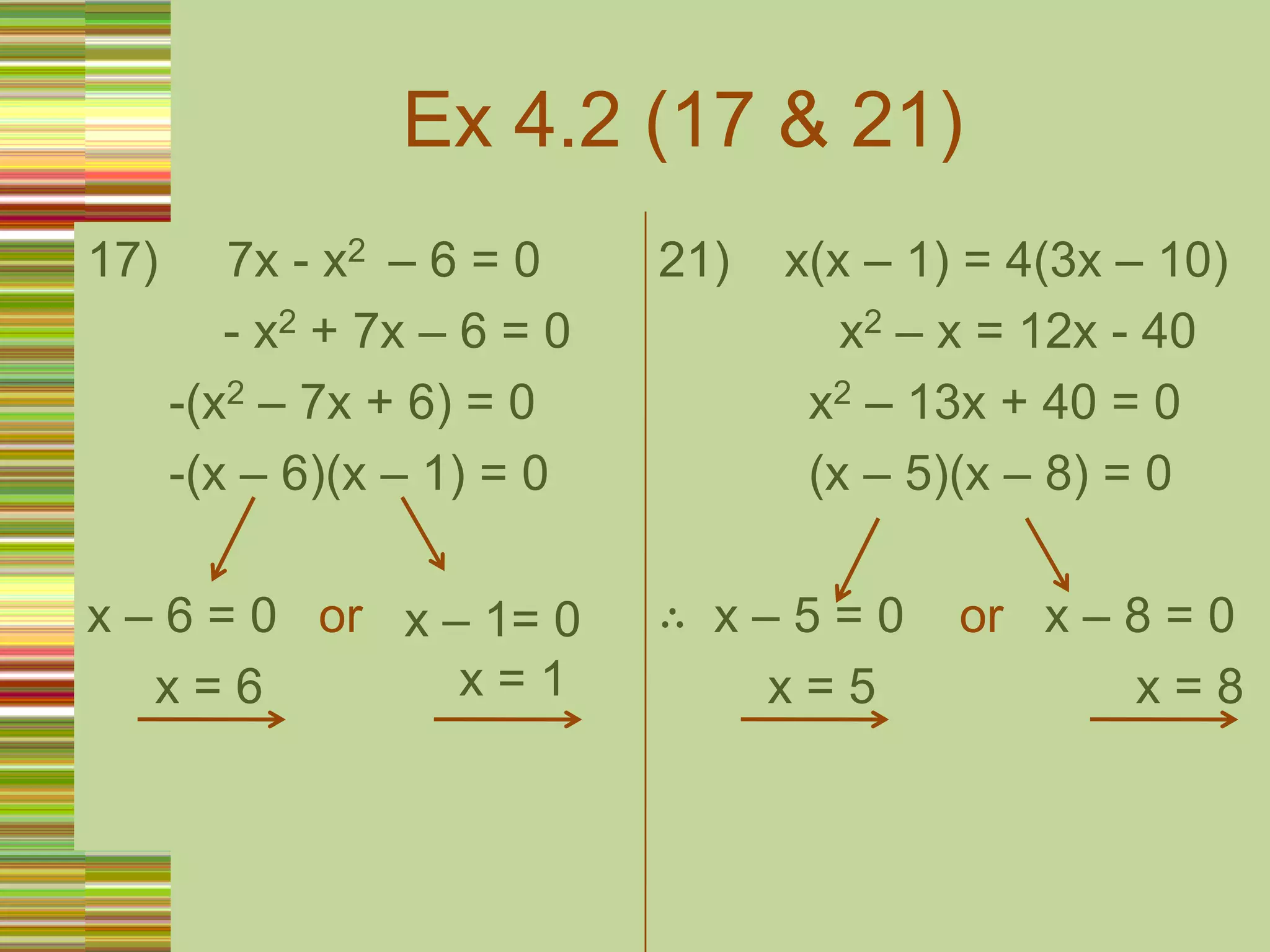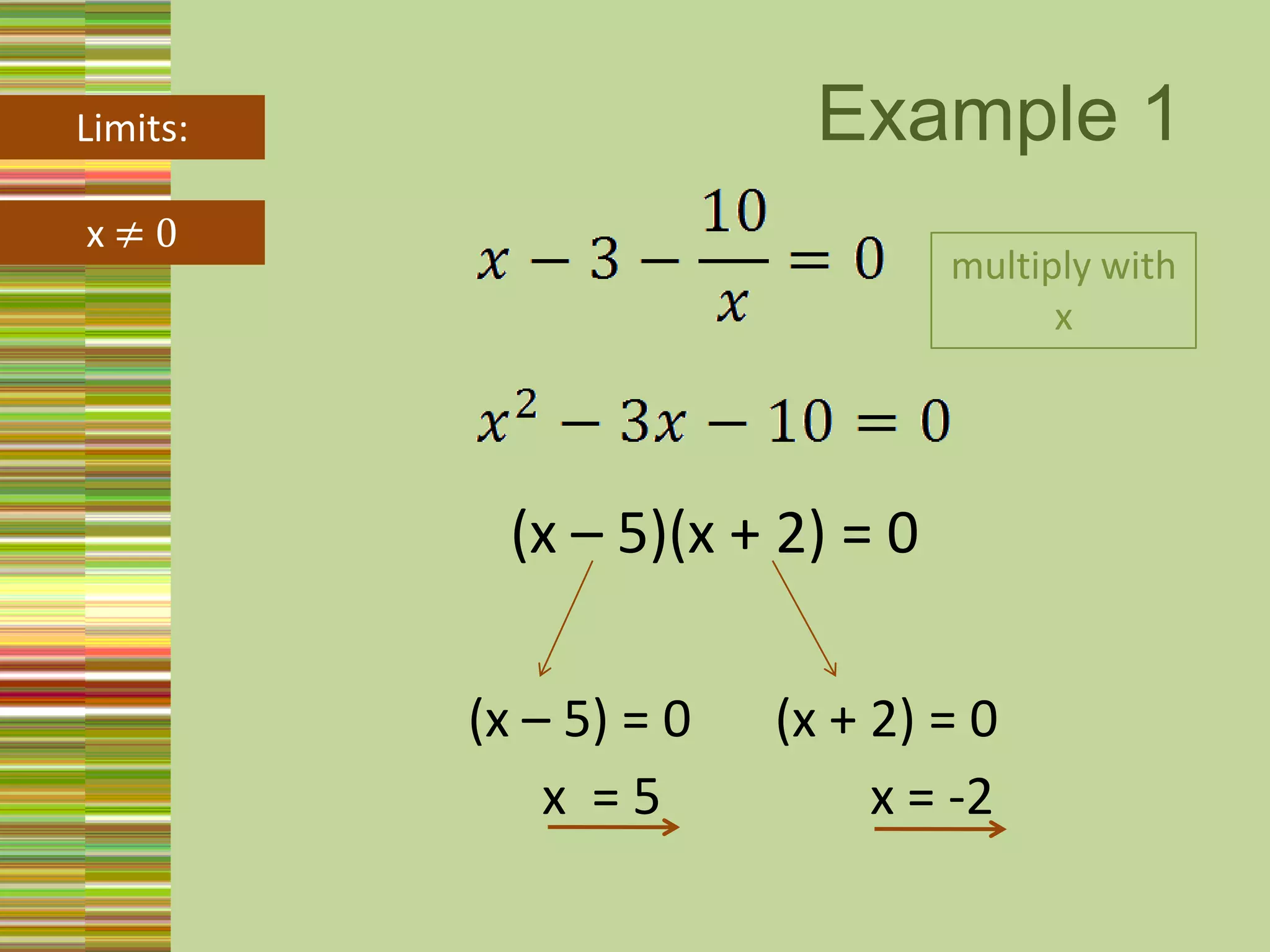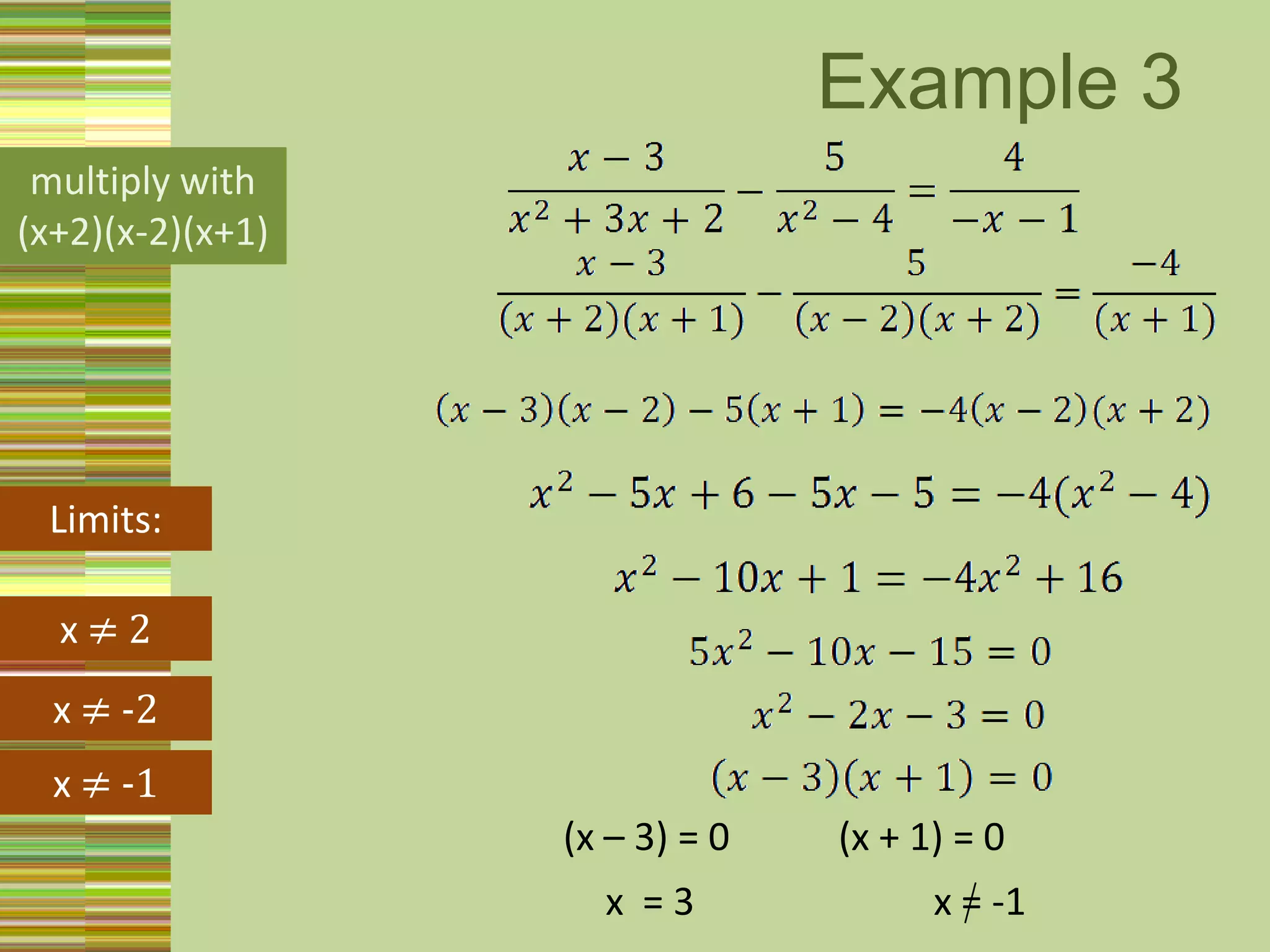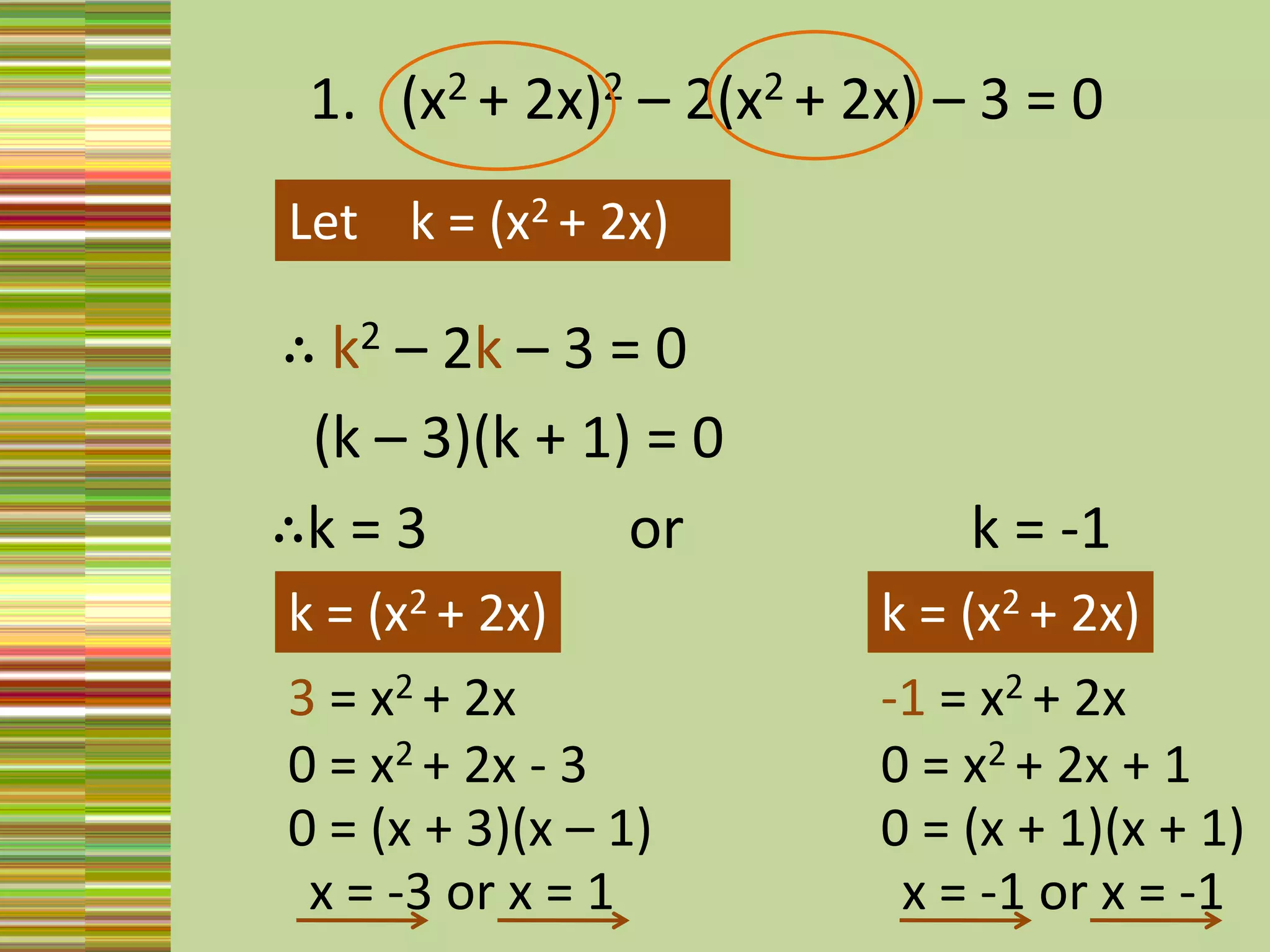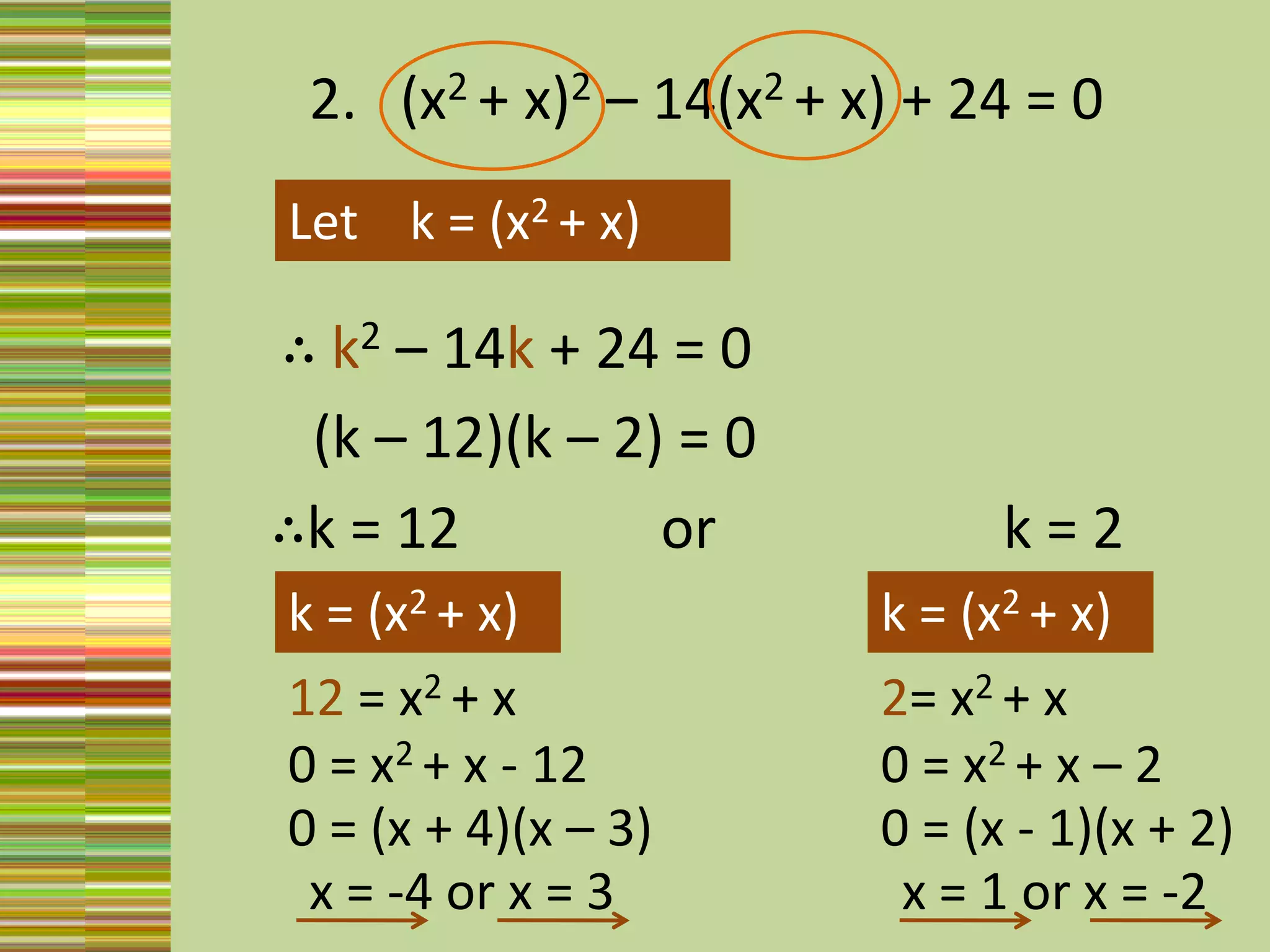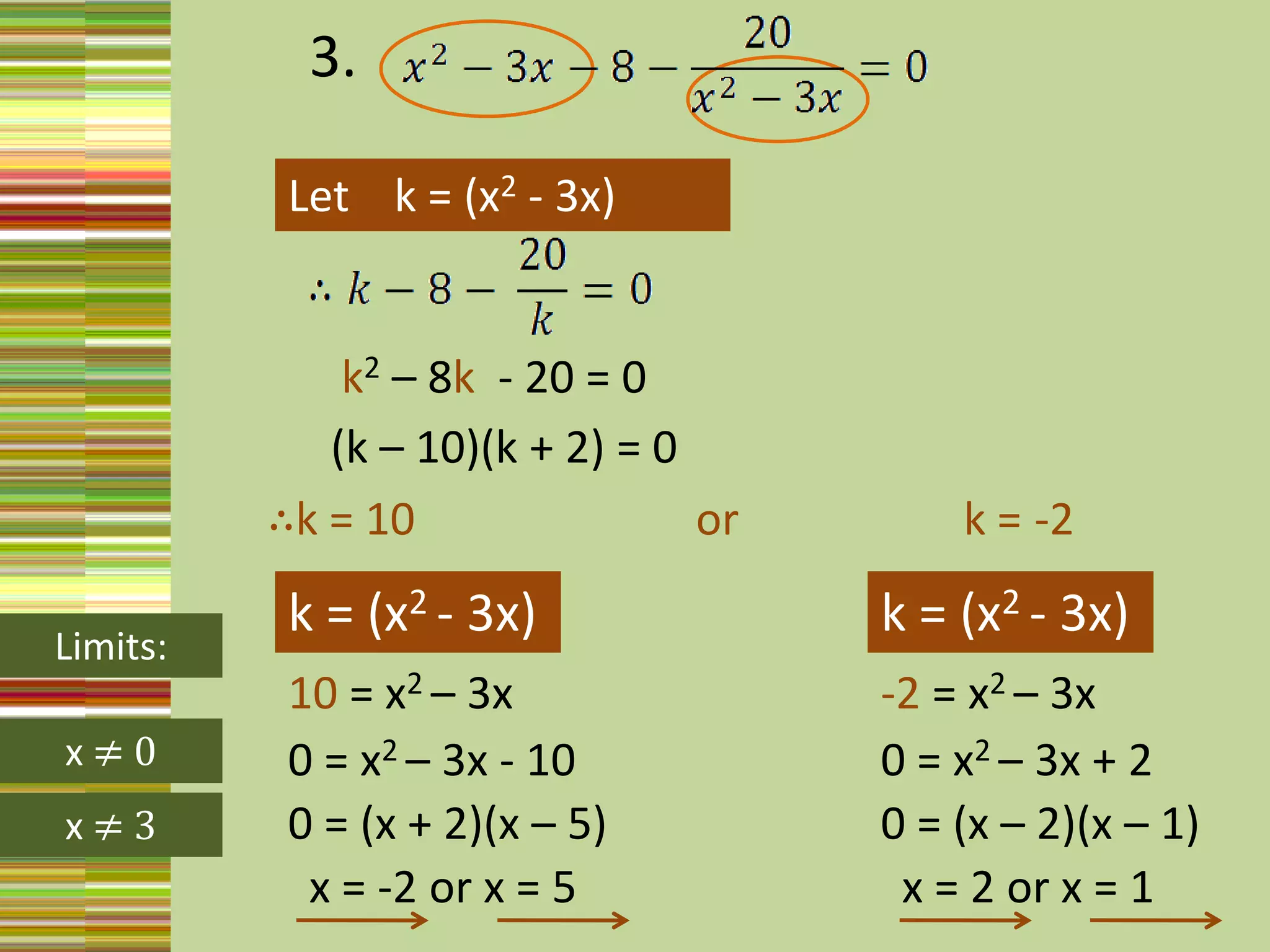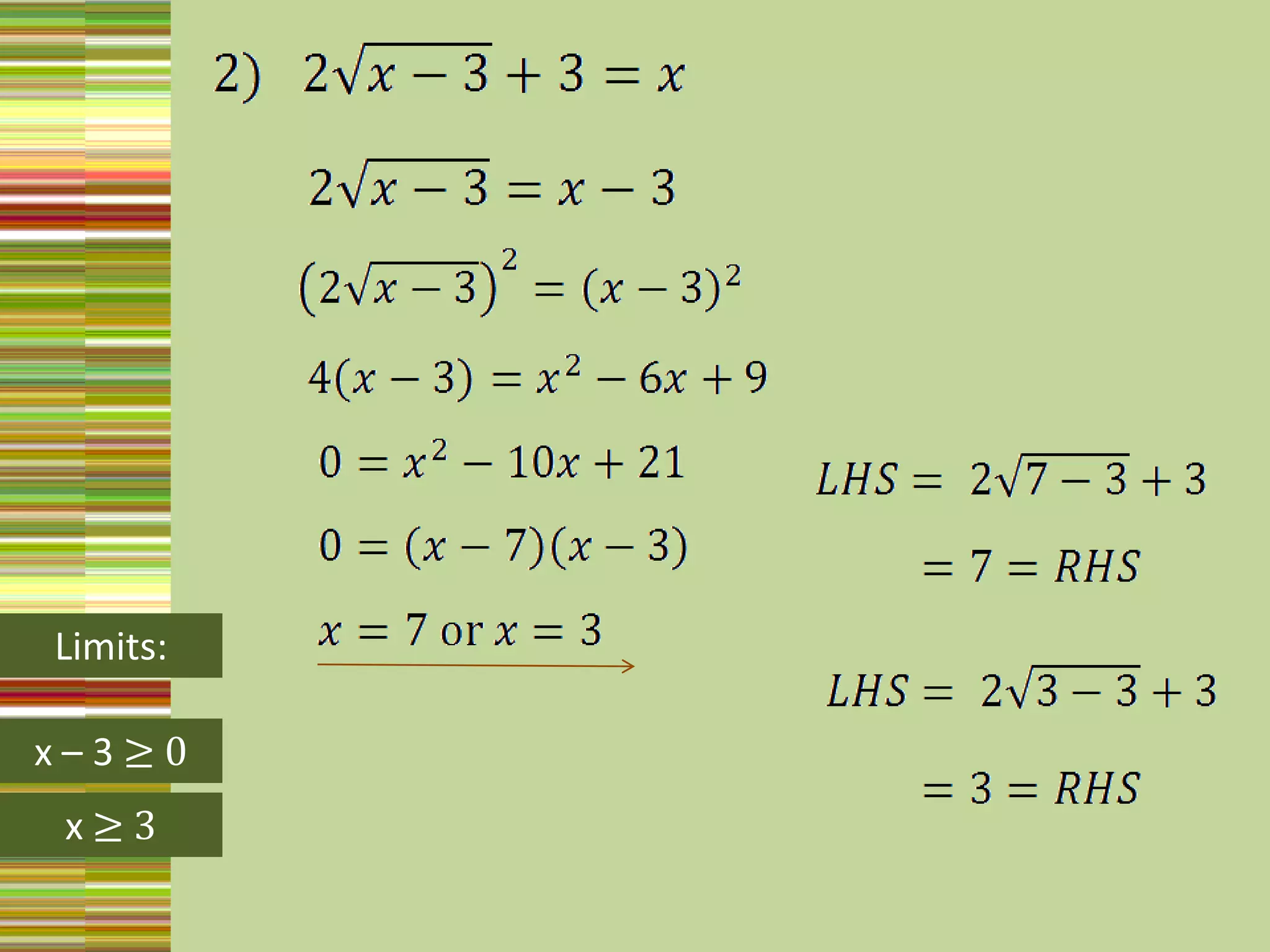Quadratic equations can be solved in several ways: 1) Factorizing, by finding two numbers whose product is the constant term and sum is the coefficient of the x term. 2) Using the quadratic formula. 3) Substitution, by letting an expression like x^2 + 2x equal a variable k, and solving the simplified equation for k and back substituting. 4) Squaring both sides, but this can introduce extraneous solutions so one must check solutions.

1. Quadratic equationsGrade 11 – Paper 1

2. Quadratic equationsQuadraticequations in one variable are equations of degree 2, whichmeans the highest power of the variable is 2.The standard formisax2 + bx + c = 0 where a ≠ 0Theseequations have 2 solutions, theycanbe:differentthe samenon-realThe solutions are known as the roots of the equation.

3. Method:The solution of quadraticequations by factorisingisbased on the factthat ifp.q = 0 theneither p or q must bezero.Thereforetherewillbe 2 solutions.*This onlyworks if the RHS is 0

4. Solve for x:x – 3 = 0(x – 3)(x + 2) = 0x(x + 7) = 0x2 - 4x = 0x2 + x – 6 = 0(x – 3)(x +5)(x – 1) = 0If ONE factor is equal to zero, the whole expression will be zero.

5. Method 1: Factorisingx2 – 2x – 35 = 0 (x – 7)(x + 5) = 0x – 7 = 0 or x = 7x(x – 1) = 20 x2 – x – 20 = 0 (x – 5)(x + 4) = 0∴ x – 5 = 0 x = 5x + 5 = 0 x = -5x + 4 = 0 x = -4

6. Example 3(x + 1)(x – 2) +3(x – 1)(x + 1) = 3(x – 2)x2 – 2x + x – 2 + 3x2 – 3 = 3x – 6 4x2 – 4x + 1 = 0 (2x – 1)(2x – 1) = 02x – 1 = 02x – 1 = 02x = 12x = 1OR x = ½ x = ½Both roots are equal

7. ClassworkPg 68 Ex 4.29, 11, 17, 21, 24

8. Ex 4.2 (9 & 11)9) 3x2 – 12 = 0 3(x2 – 4) = 0 3(x – 2)(x + 2) = 0x – 2 = 0 or x = 211) 2x2 = 18 (÷2) x2 = 9 x = ±√9 ∴ x = ±3x + 2 = 0 x = -2Remember a square root have a positive and a negative answer.

9. Ex 4.2 (17 & 21) 7x - x2 – 6 = 0 - x2 + 7x – 6 = 0 -(x2 – 7x + 6) = 0 -(x – 6)(x – 1) = 0x – 6 = 0 or x = 621) x(x – 1) = 4(3x – 10) x2 – x = 12x - 40 x2 – 13x + 40 = 0 (x – 5)(x – 8) = 0∴ x – 5 = 0 or x – 8 = 0 x = 5 x = 8 x – 1= 0 x = 1

10. Ex 4.2 (24)24) 2(m – 1)(m +1)= 0 2m2 – 2 = 7m +14 - 1 2m2 – 7m – 15 = 0 (2m + 3)(m – 5) = 02m + 3= 0 or m – 5 = 0 2m = -3 m = 5 m = -3/2Steps:Multiply out.Make the RHS = 0Factorise LHSSet each factor = 0Solve each factor.

11. Home workPg 68 Ex 4.22, 4, 7, 8,12, 13, 16, 18, 23

12. Equations with fractionsDivision by zero is undefined.Start by writing down the restrictions.Multiply with the denominator.

13. Example 1Limits:x ≠ 0multiply with x(x – 5)(x + 2) = 0(x – 5) = 0(x + 2) = 0x = 5 x = -2

14. Example 2multiply with (x-2)(x-3)(x – 4)(x – 2) = 0Limits:x ≠ 2(x – 4) = 0(x - 2) = 0x ≠ 3x = 4 x = 2

15. Example 3multiply with (x+2)(x-2)(x+1)Limits:x ≠ 2x ≠ -2x ≠ -1(x – 3) = 0(x + 1) = 0x = 3 x = -1

16. Home workPg 70 Ex 4.32, 4, 6, 10, 17

17. Method 3: Substitution(another k-method)If an algebraic expression is repeated in the equation we can replace it with “k” to make a simpler equation. Just remember to substitute back once you have calculated k.

18. 1. (x2 + 2x)2 – 2(x2 + 2x) – 3 = 0Let k = (x2 + 2x) ∴ k2 – 2k – 3 = 0 (k – 3)(k + 1) = 0∴k = 3 or k = -1k = (x2 + 2x) k = (x2 + 2x) 3 = x2 + 2x -1 = x2 + 2x 0= x2 + 2x - 30= x2 + 2x + 10= (x + 3)(x – 1)0= (x + 1)(x + 1)x = -3 or x = 1x = -1 or x = -1

19. 2. (x2 + x)2 – 14(x2 + x) + 24 = 0Let k = (x2 + x) ∴ k2 – 14k + 24 = 0 (k – 12)(k – 2) = 0∴k = 12 or k = 2k = (x2 + x) k = (x2 + x) 12 = x2 + x 2= x2 + x 0= x2 + x - 120= x2 + x – 20= (x + 4)(x – 3)0= (x - 1)(x + 2)x = -4 or x = 3x = 1 or x = -2

20. 3. Let k = (x2 - 3x) k2 – 8k - 20 = 0 (k – 10)(k + 2) = 0∴k = 10 or k = -2k = (x2 - 3x) k = (x2 - 3x) Limits:10 = x2 – 3x -2 = x2 – 3x x ≠ 00= x2 – 3x - 100= x2 – 3x + 2 0= (x + 2)(x – 5)0= (x – 2)(x – 1)x ≠ 3x = -2 or x = 5x = 2 or x = 1

21. Home workPg 72 Ex 4.42, 3, 7, 8, 9

22. Method 4: Squaring both sidesTest:1)x = 3x = -2x = 3 or x = -2 x ≠ -2Squaring both sides might introduce a extra solution which is invalid.

23. Notes:By definition is non-negative.∴ √9 = 3 and √9 ≠ -3, but x2 = 9 √x2 =√9 x = ±3The square root of a negative number is not defined.√x ∈ ℝ ⇒ x ≥ 0(a + b)2 ≠ a2 + b2 (a + b)2 = a2 + 2ab + b2

24. Limits:x – 3 ≥ 0x ≥ 3

25. Home workPg 74 Ex 4.51, 4, 5, 7, 9, 10, 11, 12