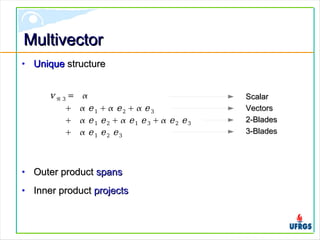
The document discusses geometric algebra, which provides a unified mathematical framework for geometry. It introduces multivectors as the unique structure in geometric algebra, formed from outer and inner products of basis vectors. Operations on multivectors like products, inversions, and joins are described. Implementations of geometric algebra aim to efficiently represent multivectors with minimal memory. The document argues geometric algebra can eliminate diverse mathematical descriptions by providing a single framework for geometric applications.

1. Geometric AlgebraGeometric Algebra
Vitor Fernando Pamplona

2. Cross Product in nD?Cross Product in nD?
• Why not?Why not?
– V1 = (1.0, 2.0, 3.0, 4.0)V1 = (1.0, 2.0, 3.0, 4.0)
– V2 = (-2.0, -3.0, -4.0, -5.0)V2 = (-2.0, -3.0, -4.0, -5.0)
I J K Q
1,00 2,00 3,00 4,00
-2,00 -3,00 -4,00 -5,00
== ??????
V1×V2=??

3. A language for geometryA language for geometry
Geometric
Concepts
Algebraic
Language
• MagnitudeMagnitude - size- size
• DirectionDirection -orientation-orientation
• SenseSense - negative/positive- negative/positive
3D
35º
x
4,20
CCW• GradeGrade - dimension- dimension

4. What we need?What we need?
• n-dimensionaln-dimensional geometric languagegeometric language
• RepresentRepresent thethe object gradeobject grade
• OperateOperate acrossacross different dimensionsdifferent dimensions
• GeometricallyGeometrically intuitiveintuitive
• WithoutWithout limitslimits
• CoordinateCoordinate freefree
• EfficientEfficient
• UnifyUnify other algebrasother algebras

5. Product of Vectors ?Product of Vectors ?
v=3e12e2
vv = 3 e1  2 e2∗3 e1  2 e2
vv = ?
vv = 9 e1 e1  6 e1 e2  6 e2 e1  4 e2 e2
e1 e1 = ?
e1 e2 = ?
e2 e1 = ?
e2 e2 = ?
v=3,2
e1
e2
v

6. Gibbs (Vector Algebra)Gibbs (Vector Algebra)
v=3e12e2
vv = 9 e1 e1  6 e1 e2  6 e2 e1  4 e2 e2
v=3,2
{ ei⋅ej = 1 i = j
ei⋅ej = ej⋅ei = 0 i ≠ j
vv = 9  4 = 13
v⋅v = 3,2∗3,2
v⋅v = 3∗3  2∗2
v⋅v = 13
dot productdot product
e1
e2
v

7. Clifford (Geometric Algebra)Clifford (Geometric Algebra)
{ ei⋅ej = 1 i = j
ei⋅ej  ej⋅ei = 0 i ≠ j
v=3e12e2
e1
e2
v
vv = 9 e1 e1  6 e1 e2  6 e2 e1  4 e2 e2
v=3,2
vv = 9  4 = 13
ei⋅ej =−ej⋅ei
vv = 9 e1 e1  6 e1 e2 − 6 e1 e2  4 e2 e2
AnticomutivityAnticomutivity
Inner productInner product

8. The Goal: Outer ProductThe Goal: Outer Product
• What'sWhat's e1e2e1e2 ??
– It isn't a scalarIt isn't a scalar
– It isn't a vectorIt isn't a vector
• It's aIt's a planeplane, a, a vector spacevector space (blade)(blade)
• CalledCalled BivectorBivector or 2-vectoror 2-vector
• Outer productsOuter products spanspan
e1
e2
O
e1
e2
CCW
2D
O
e1∧e2
e2∧e1

9. Inner product (dot)Inner product (dot)
• Outer productOuter product spansspans
• Inner productInner product projectsprojects
1 e1 ∧ 2 e2 = 1 ∗2 e1 e2
12 e1 e2 ⋅ e2 = 12 e1
vv = 9 4 = 13
vv = 9 e1 e1  6 e1 e2 − 6 e1 e2  4 e2 e2
e1
e2
v

10. Geometric ProductGeometric Product
vu =v ⋅u v ∧ u
Inner productInner product Outer productOuter product
v ∥u  v ∧ u = 0
v ⊥ u  v ⋅ u = 0
vv =9  4 =13
vv =9 e1 e1 6 e1 e2 −6 e1 e2  4 e2 e2
e1
e2
v
{ ei ⋅e j = 1 i = j 
ei⋅e j  e j⋅ei = 0 i ≠ j 

11. Contraction Inner ProductContraction Inner Product
• GeneralizesGeneralizes inner product to Bladesinner product to Blades
• Complement of the orthogonal projectionComplement of the orthogonal projection
• GeneralizingGeneralizing geometric productgeometric product
BB
a Ba B =
aa
a Ba B
vu = v u  v ∧ u

12. History of Geometric AlgebraHistory of Geometric Algebra
Synthetic GeometrySynthetic Geometry
EuclidEuclid
Analitic GeometricAnalitic Geometric
DescartesDescartes
Complex ÁlgebraComplex Álgebra
Wessel, GaussWessel, Gauss
QuaternionsQuaternions
HamiltonHamilton
Matrix ÁlgebraMatrix Álgebra
CayleyCayley
DeterminantsDeterminants
SylvesterSylvester
Vector AlgebraVector Algebra
GibbsGibbs
Exterior AlgebraExterior Algebra
GrassmanGrassman
Clifford AlgebraClifford Algebra
CliffordClifford
Differential FormsDifferential Forms
E. CartanE. CartanSpin AlgebraSpin Algebra
Pauli, DiracPauli, Dirac
Tensor AlgebraTensor Algebra
RicciRicci
Geometric AlgebraGeometric Algebra
300 BC
1637
1798
1854
1878
1928
1843
1844
18781881
1890 1923

13. MultivectorMultivector
• UniqueUnique structurestructure
• Outer productOuter product spansspans
• Inner productInner product projectsprojects
v ℜ 3 = 
  e1   e2   e3
  e1 e2   e1 e3   e2 e3
  e1 e2 e3
ScalarScalar
VectorsVectors
2-Blades2-Blades
3-Blades3-Blades

14. Operations on MultivectorsOperations on Multivectors
• Graduated InvolutionGraduated Involution
• ReverseReverse
• ConjugationConjugation
• InverseInverse
v k =−1
k
∗v k
v k =−1
k k − 1/2
∗v k  vu = uv
v k = v = v
v −1
=
v
∣v∣²

15. Operations on Multivectors (cont)Operations on Multivectors (cont)
• AngleAngle between vectorsbetween vectors
• PseudoscalarPseudoscalar
– Dimensional limitDimensional limit
• DualDual
cos  =
v⋅u
∣v∣∣u∣
A=Ãk∗ps
psℜ3=1∗e1∧e2∧e3

16. Operations on Multivectors (cont 2)Operations on Multivectors (cont 2)
• MeetMeet
• JoinJoin
• Sum and differenceSum and difference
• NablaNabla = Symmetric difference= Symmetric difference
C=A∩B
C=A∪B
v1 ∇ v2=majorGradev1∗v2
C=AB C=A−B

17. Future ReadingsFuture Readings [Dorst,[Dorst, 02a02a] [Vaz,] [Vaz, 9797]]
• Projection of blades andProjection of blades and RejectionRejection
• ReflectionReflection
• RotorsRotors
• ModelsModels
– HomogeneousHomogeneous model / Plücker coordinatesmodel / Plücker coordinates
– ConformalConformal modelmodel
• QuaternionsQuaternions

18. GA FrameworksGA Frameworks
• GAViewerGAViewer: Geometric algebra computations and visualize: Geometric algebra computations and visualize
• GAPGAP: Geometric Algebra Package: Geometric Algebra Package [[Zaharia, 03Zaharia, 03]]
• GAIGEN: Code generator to Geometric AlgebraGAIGEN: Code generator to Geometric Algebra [[FontijneFontijne]]
• GluCat:GluCat: template classes to Clifford algebrastemplate classes to Clifford algebras
• GAGL:GAGL: Geometric Algebra to OpenGLGeometric Algebra to OpenGL
• GEOMA: C++ Template Classes for Geometric AlgebrasGEOMA: C++ Template Classes for Geometric Algebras

19. Multivector ImplementationsMultivector Implementations
• GAGLGAGL
– Vector[8]Vector[8]
– Only in 3D.Only in 3D.
• GEOMAGEOMA
– Matrix [2Matrix [2kk
][2][2kk
]] where k = gradewhere k = grade
• GluCat:GluCat: ????
• GAPGAP
scalar , e1 , e2 , e3 ,
e1∧e2 , e1∧e3 , e2∧e3 ,
e1∧e2∧e3
scalar , e1 , e2 , e3 , e1∧e2 , e1∧e3 , e2∧e3 , e1∧e2∧e3
HMV HMV HMV
EBLADE EBLADE EBLADE

20. Clean Multivector ImplementationClean Multivector Implementation
• Think OOThink OO with low memory usagewith low memory usage
• Two ClassesTwo Classes
– GAMultivectorGAMultivector
– GASpaceGASpace
• Inside GAMultivectorInside GAMultivector
– double[length]: where length is adouble[length]: where length is a compile timecompile time methodmethod
length=1∑
k=1
n
Cn ,k

21. Performance AspectsPerformance Aspects
Model Implem. Full Rend Time (s) Memory (MB)
3DLA Standard 1,00 6,2
3DGA Gaigen 2,56 6,7
4DLA Standard 1,05 6,4
4DGA Gaigen 2,97 7,7
5DGA Gaigen 5,71 9,9
• RaytracerRaytracer benchmarkbenchmark
• 3DLA: Linear Algebra3DLA: Linear Algebra
• 3DGA: Geometric Algebra3DGA: Geometric Algebra
• 4DLA: Homogeneous coordinates4DLA: Homogeneous coordinates
• 4DGA: Homogeneous model4DGA: Homogeneous model
• 5DGA: Conformal model5DGA: Conformal model
FASTFAST
ELEGANCEELEGANCE
(Fontijne, D. & Dorst,2003)

22. So...So...
““... that it provides a single, simple mathematical framework... that it provides a single, simple mathematical framework
which eliminates the plethora of diverse mathematicalwhich eliminates the plethora of diverse mathematical
descriptions and techniques...”descriptions and techniques...”
[McRobie and Lasenby, 1999][McRobie and Lasenby, 1999]

23. ReferencesReferences
• Dorst, L. & Mann, S. Geometric algebra: a computational framework for geometricalDorst, L. & Mann, S. Geometric algebra: a computational framework for geometrical
applications (part II: aplications) IEEE Computer Graphics and Applications, 2002, 1applications (part II: aplications) IEEE Computer Graphics and Applications, 2002, 1
• Dorst, L. & Mann, S. Geometric algebra: a computational framework for geometricalDorst, L. & Mann, S. Geometric algebra: a computational framework for geometrical
applications (part I: algebra) IEEE Computer Graphics and Applications, 2002, 1, 24-31applications (part I: algebra) IEEE Computer Graphics and Applications, 2002, 1, 24-31
• Fontijne, D. & Dorst, L. Modeling 3D Euclidean Geometry IEEE Computer Graphics andFontijne, D. & Dorst, L. Modeling 3D Euclidean Geometry IEEE Computer Graphics and
Applications, 2003Applications, 2003
• Macdonald, A. A Survey of Geometric Algebra and Geometric Calculus, 2005Macdonald, A. A Survey of Geometric Algebra and Geometric Calculus, 2005
• Vaz, J.J. A álgebra geométrica do espaço euclidiano e a teoria de Pauli RevistaVaz, J.J. A álgebra geométrica do espaço euclidiano e a teoria de Pauli Revista
Brasileira de Ensino de Física, 1997, 19, 234-259Brasileira de Ensino de Física, 1997, 19, 234-259
• Zaharia, M.D. & Dorst, L. The Interface Spec. and Implementation Internals of aZaharia, M.D. & Dorst, L. The Interface Spec. and Implementation Internals of a
Program Module for Geometric Algebra University of Amsterdam, 2003Program Module for Geometric Algebra University of Amsterdam, 2003