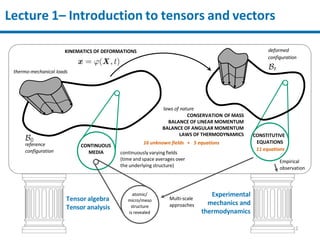
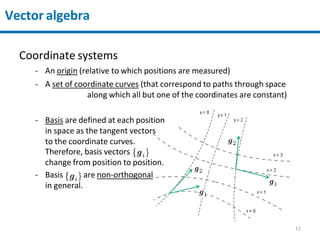
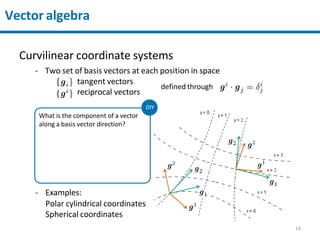
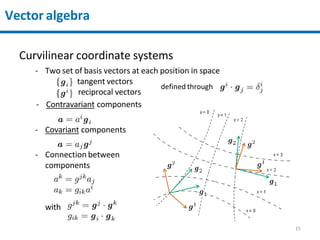
This lecture introduces tensors and vectors through the following points: 1) Tensors are abstract mathematical entities that generalize the concept of vectors. Vectors are first-order tensors. 2) Coordinate systems like Cartesian and curvilinear coordinates are discussed. Vector components can be transformed between different coordinate systems. 3) Higher-order tensors are defined as real-valued multilinear functions of vectors, generalizing first-order tensors (vectors). Component transformations preserve the coordinate-invariant nature of tensors.

1. FACULTY: Asst Prof. Shaibal Sahoo
Lecture 1
Introduction to vectors and tensors
ENGINEERING MECHANICS

2. Lecture 1– Introduction to tensors and vectors
KINEMATICS OF DEFORMATIONS
2
deformed
configuration
thermo-mechanical loads
laws of nature .
CONSERVATION OF MASS
BALANCE OF LINEAR MOMENTUM
BALANCE OF ANGULAR MOMENTUM
LAWS OF THERMODYNAMICS
reference
configuration
CONTINUOUS
MEDIA
5 equations
16 unknown fields +
continuously varying fields
(time and space averages over
the underlying structure)
CONSTITUTIVE
EQUATIONS
11 equations
Empirical
observation
Tensor algebra
Tensor analysis
atomic/
micro/meso
structure
is revealed
Multi-scale
approaches
Experimental
mechanics and
thermodynamics

3. Lecture 1– Introduction to tensors and vectors
Review:
3
DIY

4. What is a tensor?
4
- Tensors are abstract mathematical entities.
- Vectors are first order tensors.
- Vectors and tensors exist separately of a particular
coordinate system (i.e., they are coordinate invariant).
… so let’s start by reviewing Vector Algebra.

5. Vector algebra
DIY
Which is the name of each property?
5
Vector space

6. Vector algebra
Vector space – Euclidean Space
- In continuum mechanics, we restrict attention to
finite-dimensional spaces.
- We also need additional geometric properties,
such as distances and angles.
… but …
- What is an n-dimensional vector space?
- What is a distance?
- What is an angle?
Naturally, you have a good intuitive understanding of
these concepts, but we will formalize them with
the purpose of understanding their generalization.
Euclidean
Space
6

7. Vector algebra
What is an n-dimensional vector space?
- Linear independent vectors
- Given a vector space, the largest possible number of
linearly-independent vectors is the dimensionality of
the vector space.
- Any set of
a basis of
linearly independent vectors can be selected as
.
- Every vector can be written as a unique linear combination of
the basis vectors.
7

8. Vector algebra
What is a distance? What is an angle?
- Both can be defined from geometric interpretations of
an inner product and a norm.
8

9. Vector algebra
What is a distance? What is an angle?
- Both can be defined from geometric interpretations of
an inner product and a norm.
- Euclidean space:
Euclidean
Space
DIY
9
Let’s recall addition and multiplication in

10. Vector algebra
Euclidean
Space
What is a distance? What is an angle?
- Both can be defined from geometric interpretations of
an inner product and a norm.
- Euclidean space
- Euclidean point space
- Now we can naturally extend the notion of distance and angle to:
+ Distance between two points
+ Angle formed by three points
10

11. Vector algebra
Coordinate systems
- An origin (relative to which positions are measured)
- A set of coordinate curves (that correspond to paths through space
along which all but one of the coordinates are constant)
11

12. Vector algebra
Coordinate systems
- An origin (relative to which positions are measured)
- A set of coordinate curves (that correspond to paths through space
along which all but one of the coordinates are constant)
- Basis are defined at each position
in space as the tangent vectors
to the coordinate curves.
Therefore, basis vectors
change from position to position.
- Basis are non-orthogonal
in general.
12

13. Vector algebra
DIY
What is the component of a vector (or the coordinate of a position vector)
along a basis vector direction?
Coordinate systems
- If the coordinate curves are straight lines then the system is a
rectilinear coordinate system.
- If the basis vectors of a rectilinear coordinate system are orthogonal
then the system is a Cartesian coordinate system.
- If the basis vectors (or axes) of a Cartesian coordinate system are
unit vectors then the basis are called orthonormal and
follow the the condition
- We will choose basis vectors that form a right-handed triad
13

14. Vector algebra
Curvilinear coordinate systems
- Two set of basis vectors at each position in space
tangent vectors
reciprocal vectors
defined through
DIY
What is the component of a vector
along a basis vector direction?
- Examples:
Polar cylindrical coordinates
Spherical coordinates
14

15. Vector algebra
Curvilinear coordinate systems
- Two set of basis vectors at each position in space
tangent vectors
reciprocal vectors
- Contravariant components
- Covariant components
- Connection between
components
with
defined through
15

16. Vector algebra
Curvilinear coordinate systems
- All vector and tensor related operations (and continuum mechanics in
general) can be defined in curvilinear coordinate systems
- Example: the dot product
16
Note:and are
components of
the metric tensor.
We will mostly limit ourselves to Cartesian coordinate systems

17. Vector algebra
Change of basis (… back to Cartesian systems)
- Two orthonormal bases and
- The goal is to change bases from
- A linear transformation matrix
to
is defined as
DIY
17
Let’s write the transformation
using a column-matrix notation.
Show the following properties:

18. Vector algebra
Vector component transformation
- We opened this Lecture by saying that
Vectors and tensors are coordinate invariant, i.e., invariant with
respect to component transformation.
DIY
18
Prove the following transformation rules

19. Vector algebra
Vector component transformation
- We opened this Lecture by saying that
Vectors and tensors are coordinate invariant, i.e., invariant with
respect to component transformation.
- A vector can be expressed as components in
Alternatively, it can be replaced by a linear mapping
.
which returns a real number equal to the projection of the vector
on . Therefore, when evaluated on orthonormal Cartesian basis,
it returns the coordinates of the vector
19

20. DIY
From first order to n-th order tensors
- A first order tensor (vector) is a real-valued linear function of vectors
- An n-th order tensor is a real-valued n-linear function of vectors
- The components of a second-order tensor in a particular basis
are then defined as
20