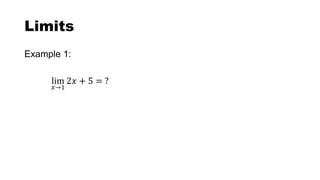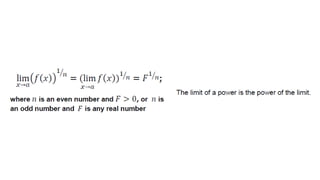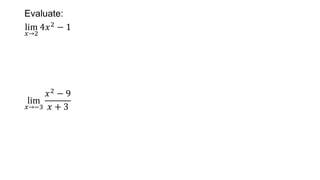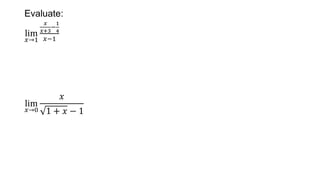This document defines key terms related to functions, limits, and graphs. It explains that a domain is the set of input values for a function, while the range is the set of possible output values. A function assigns each input a single output. Limits describe the behavior of a function as the input approaches a value, without reaching it. Examples demonstrate evaluating limits of various polynomial functions as the variable approaches a value.

1. Functions, Limits,
and Graphs
CEE 101 – Engineering Calculus 1

2. Definition of Terms
• Domain - is the set of all values that can be plugged into a function
and have the function exist and have a real number for a value.
• Range – is the set of all possible values that a function can take.
• Variable - It is a quantity which, during any set of mathematical
operations, does not retain the same value but is capable of
assuming different values.
• Constant - It is a quantity which, during any set of mathematical
operations, retains the same value.
• Polynomial - It can have constants, variables, and exponents, but
never division by a variable
• Conjugate - It is formed by changing the sign between two terms.

3. Functions
A function 𝑓 is a rule that assigns to every number 𝑥 in a collection D,
a number 𝑓(𝑥). The set D is called the domain of the function. And 𝑓(𝑥
) is called the value of a function at 𝑥, or commonly known as range.
The set of ordered pair (𝑥, 𝑓(𝑥)) is called the graph of 𝑓.
• 𝑓(𝑥) = 𝑥2 + 2 is a function; it yields exactly one possible value.
• [𝑓(𝑥)]2 = 𝑥 + 2 is not a function; at specific value of x, there are
two values

4. Limits
It is a fundamental concept used to describe the behavior of a
function as its input approaches a certain value.
The limit of a function 𝑓(𝑥) as 𝑥 approaches 𝑎 is 𝐿, can be written as
lim
𝑥→𝑎
𝑓 𝑥 = 𝐿
In other words, the value of the function 𝑓(𝑥) gets closer and closer
to 𝐿 as 𝑥 gets closer and closer to 𝑎, without being exactly equal to
𝑎.

5. Limits
Example 1:
lim
𝑥→1
2𝑥 + 5 = ?

6. Properties of Limits

9. Evaluate:
lim
𝑥→2
4𝑥2
− 1
lim
𝑥→−3
𝑥2 − 9
𝑥 + 3

10. Evaluate:
lim
𝑥→1
𝑥
𝑥+3
−
1
4
𝑥−1
lim
𝑥→0
𝑥
1 + 𝑥 − 1

11. Evaluate:
lim
𝑥→−∞
2𝑥2+3
𝑥2−5𝑥−1
lim
𝑥→+∞
8𝑥2
𝑥+5