1. The document discusses mathematics and defines key mathematical concepts such as expressions, operands, operations, relations, and polynomials.
2. It explains that mathematics can be viewed as a language for describing the universe, and algebra as a system for constructing well-formed mathematical expressions.
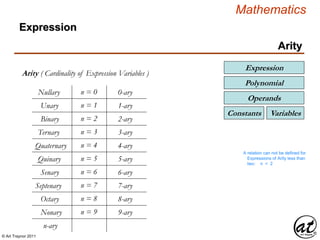
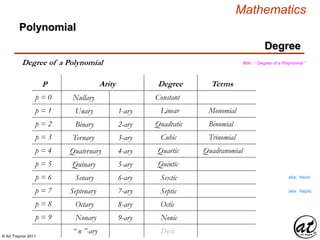
3. Key terms are defined, such as the arity and degree of polynomials, and the different types of expressions like nullary, unary, binary, and n-ary expressions. Operand parity and polynomial structure criteria are also discussed.




![© Art Traynor 2011
Mathematics
Definitions
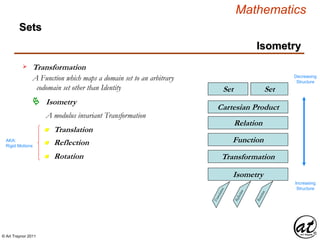
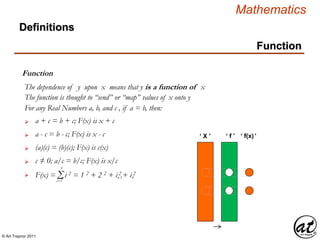
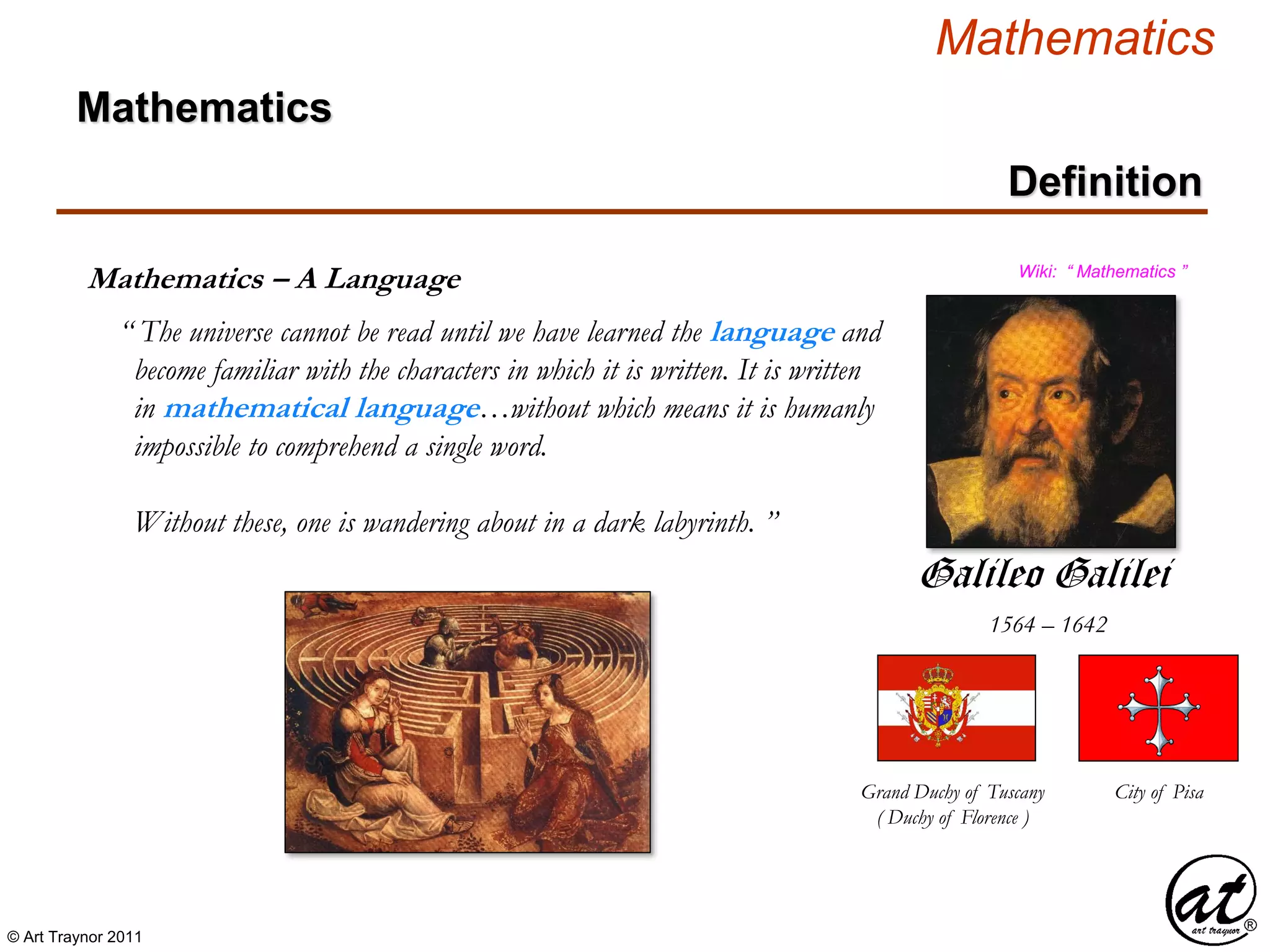
Expression
Symbol Operation Relation
Expression – A Mathematical Sentence
Proposition Formula
VariablesConstants
Operands ( Terms )
Equation
A formula stating an
equivalency class relation
Linear Equation
An equation in which each term is either
a constant or the product of a constant
and (a) variable[s] of the first degree
Mathematics
Polynomial](https://image.slidesharecdn.com/3e55d42e-4b83-4886-bc78-169d0f14feb0-160620081412/85/Function_160416_01-6-320.jpg)












![© Art Traynor 2011
Mathematics
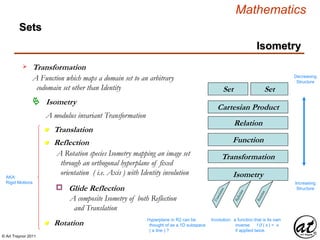
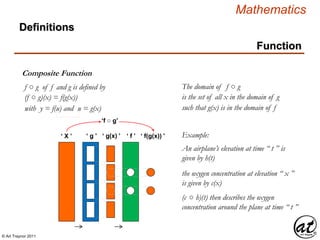
Linear Equation
Linear Equation
Equation
An Equation consisting of:
Operands that are either
Any Variables are restricted to the First Order n = 1
Linear Equation
An equation in which each term
is either a constant or the
product of a constant and (a)
variable[s] of the first order
Expression
Proposition
Equation
Formula
n Constant(s) or
n A product of Constant(s) and
one or more Variable(s)
The Linear character of the Equation derives from the
geometry of its graph which is a line in the R2 plane
As a Relation the Arity of a Linear Equation must be
at least two, or n ≥ 2 , or a Binomial or greater Polynomial
Polynomial](https://image.slidesharecdn.com/3e55d42e-4b83-4886-bc78-169d0f14feb0-160620081412/85/Function_160416_01-21-320.jpg)
![© Art Traynor 2011
Mathematics
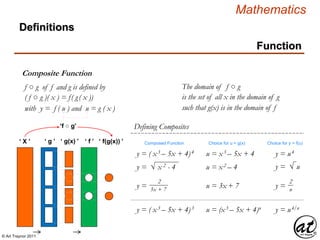
Equation
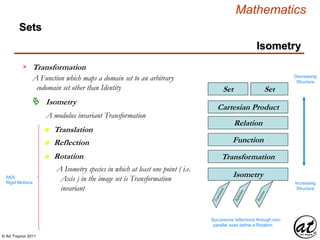
Linear Equation
Linear Equation
An equation in which each term is either a constant or the product
of a constant and (a) variable[s] of the first order
Term ai represents a Coefficient
b = Σi= 1
n
ai xi = ai xi + ai+1 xi+1…+ an – 1 xn – 1 + an xn
Equation of a Line in n-variables
A linear equation in “ n ” variables, xi + xi+1 …+ xn-1 + xn
has the form:
n Coefficients are distributed over a defined field
(e.g. N , Z , Q , R , C )
Term xi represents a Variable ( e.g. x, y, z )
n Term a1 is defined as the Leading Coefficient
n Term x1 is defined as the Leading Variable
Section 1.1, (Pg. 2)
Section 1.1, (Pg. 2)
Section 1.1, (Pg. 2)
Section 1.1, (Pg. 2)
Coefficient = a multiplicative factor
(scalar) of fixed value (constant)
Section 1.1, (Pg. 2)](https://image.slidesharecdn.com/3e55d42e-4b83-4886-bc78-169d0f14feb0-160620081412/85/Function_160416_01-22-320.jpg)
![© Art Traynor 2011
Mathematics
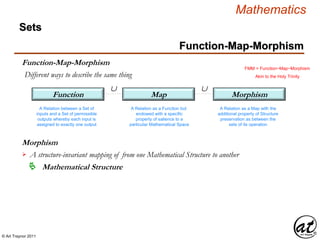
Linear Equation
Equation
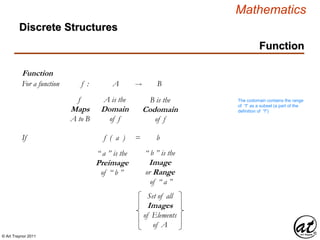
Standard Form ( Polynomial )
Ax + By = C
Ax1 + By1 = C
For the equation to describe a line ( no curvature )
the variable indices must equal one
ai xi + ai+1 xi+1 …+ an – 1 xn –1 + an xn = b
ai xi
1 + ai+1 x 1 …+ an – 1 x 1 + a1 x 1 = bi+1 n – 1 n n
ℝ
2
: a1 x + a2 y = b
ℝ
3
: a1 x + a2 y + a3 z = b
Blitzer, Section 3.2, (Pg. 226)
Section 1.1, (Pg. 2)
Test for Linearity
A Linear Equation can be expressed in Standard Form
As a species of Polynomial , a Linear Equation
can be expressed in Standard Form
Every Variable term must be of precise order n = 1
Linear Equation
An equation in which each term
is either a constant or the
product of a constant and (a)
variable[s] of the first order
Expression
Proposition
Equation
Formula
Polynomial](https://image.slidesharecdn.com/3e55d42e-4b83-4886-bc78-169d0f14feb0-160620081412/85/Function_160416_01-23-320.jpg)