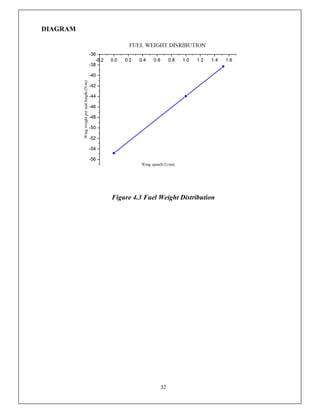
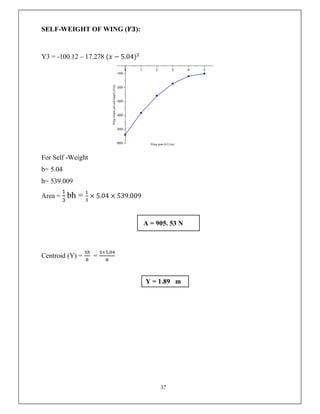
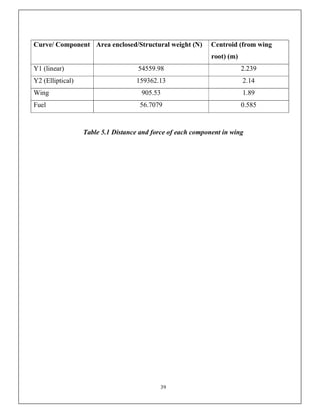
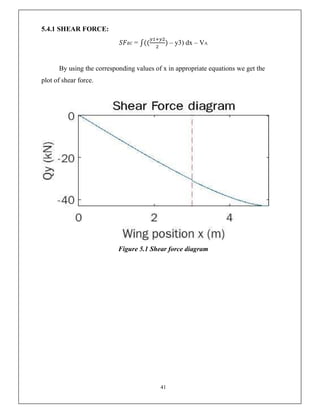
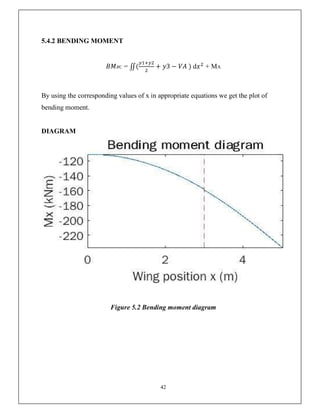
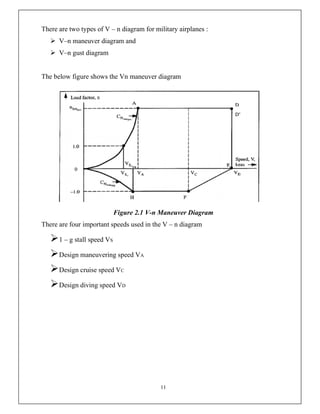
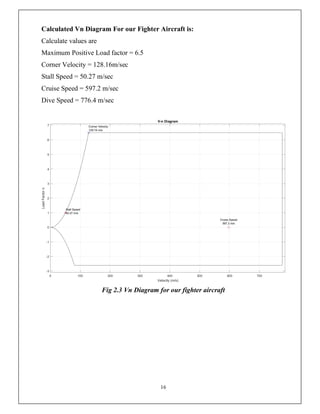
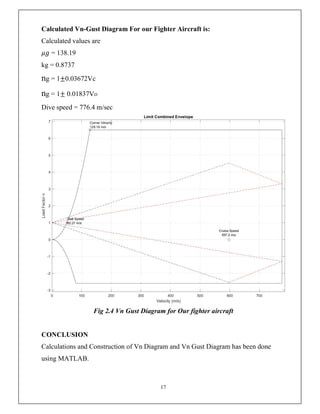
This document discusses the V-n diagram, which plots the velocity of an aircraft against the load factor it experiences. It outlines how load factors are calculated based on the lift and weight of the aircraft. Limit, proof and ultimate load factors are explained which specify the maximum loads aircraft structures must be designed to withstand. Typical load factors for different aircraft types are shown, with fighters experiencing the highest positive load factors due to high-performance maneuvering. The V-n diagram defines the flight envelope and structural limits for an aircraft.

1. DESIGN OF FIGHTER AIRCRAFT
AIRCRAFT DESIGN PROJECT- II
Submitted by
DUDEKULA JAMAL (18101147)
In partial fulfilment for the award of the
degree of
BACHELOR OF TECHNOLOGY
IN
AERONAUTICAL ENGINEERING
SCHOOL OF AERONAUTICAL SCIENCES
HINDUSTAN INSTITUTE OF TECHNOLOGY AND SCIENCE
PADUR, CHENNAI – 603103
OCTOBER 2021

2. HINDUSTAN INSTITUTE OF TECHNOLOGY AND SCIENCE
PADUR, CHENNAI – 603103
BONAFIDE CERTIFICATE
Certified that this project report “DESIGN OF FIGHTER AIRCRAFT” is the
bonafide work of “DUDEKULA JAMAL”, who carried out the project work
under my supervision. Certified further that to the best of my knowledge the
work reported here does not form part of any other project/research work on the
basis of which a degree or award was conferred on an earlier occasion on this or
any other candidate.
Dr. R. ASOKAN Ms. RANJITHA E
Professor& Head of the department Assistant Professor
department of aeronautical sciences department of aeronautical sciences
Hindustan Institute of Technology Hindustan Institute of Technology
and Science and Science
Chennai – 603103 Chennai – 603103
Submitted for the project viva voice Examination heldon: 05-10-2021
Internal Examiner External Examiner

3. ACKNOWLEDGEMENT
It’s my extreme pleasure to thank our chairperson Dr. Elizabeth Verghese,
Hindustan Institute of Technology & Science, for providing me with a good,
pleasing and safe environment in our college which helped me a lot to carry on
with my project.
I wish to express my heartfelt gratitude to Dr. S.N. SRIDHARA, Vice-
Chancellor, Hindustan Institute of Technology & Science for providing me with
an excellent study environment.
I am thankful to Dr. R. Asokan, Professor& Head of the Department, School of
Aeronautical Sciences for much of his valuable support, encouragement in
carrying out this work.
I would like to thank my internal guide Ms. RANJITHA E, for continuously guiding
and actively participating in my project, giving valuable suggestions to complete the
project work.
I would like to thank all the technical and teaching staff of Aeronautical
Department, who extended their support directly or indirectly.
Last, but not the least, I am deeply indebted to my parents who have been the
greatest support while I worked day and night for the project to make it a success.

4. TABLE OF CONTENT
CHAPTER TITLE PAGE NO
ABSTRACT I
LIST OF TABLES II
LIST OF FIGURES III
LIST OF SYMBOLS AND ABBREVIATIONS V
1 SUMMARY FROM AIRCRAFT DESIGN PROJECT – I 1
2 V-n DIAGRAM 9
2.1 GUST V - n DIAGRAM 12
3 SCHRENK’S CURVE 18
4 WING LOAD ESTIMATION 25
5 SHEAR FORCE AND BENDING MOMENT DIAGRAM 34
6 TYRE ANALYSIS 43
7 LANDING GEAR ANALYSIS 47
8 CONCLUSION 52
9 REFERENCE 53

5. I
ABSTRACT
In aircraft design project – I, we have calculated weight estimation, powerplant
selection, airfoil selection and wing design parameters. We have also done the
performance analysis of fighter aircraft during landing and take-off. In aircraft design
project - II, taking the values obtained in design project - I as input, the load factors during
various phases of flight is calculated and the V-n maneuver diagram is drawn which is
most needed for fighter aircraft since it known for maneuverability, the load distribution
on the wing is found and the shear force diagram and the bending moment diagram for
the wing.
We have done the undercarriage analysis of fighter aircraft. The tyre selection
and efficiency of shock absorber. The values are taken from the aircraft design project -
I and are used in the aircraft design project – II.
Keywords: Fighter aircraft, supersonic, bending moment, maneuverability

6. II
LIST OF TABLES
TABLE NO TITLE PAGE NO
1.1 Final design parameters 6
1.2 Weight parameters 7
1.3 Lift and drag parameters 7
1.4 Performance parameters 7
1.5 Wing design parameters 7
2.1 Typical Limit load factors for different aircrafts 8
4.1 Overall Load Acting on the Wing Structure 33
5.1 Distance and forces of each component of wing 39
6.1 Statical Tire Sizing 44
6.2 Recommended Tire Pressure 44
7.1 Shock Absorber Efficiency 49
7.2 Gear Load Factor 49

7. III
LIST OF FIGURES
FIGURE NO TITLE PAGE NO
1.1 Mission Profile for fighter aircraft 1
1.2 Side view of Fighter Aircraft 4
1.3 Top view of Fighter Aircraft 4
1.4 Front view of Fighter Aircraft 5
1.5 Isometric view of Fighter aircraft 5
2.1 Model V-n Maneuver Diagram 11
2.2 Model Gust V-n diagram 13
2.3 V-n diagram 16
2.4 Gust V-n diagram 17
3.1 Typical linear lift distribution 19
3.2 linear lift distribution 21
3.3 Typical Elliptic lift distribution 22
3.4 Elliptic lift distribution 23
3.5 Schrenk’s Curve 24
4.1 Self-Weight Distribution 28
4.2 Fuel tank dimensions 29
4.3 Fuel Weight Distribution 32
4.4 Overall Weight Distribution 33
5.1 Shear Force Diagram 41
5.2 Bending Moment Diagram 42
6.1 Tire Contact Area 43
7.1 Tri-cycle Landing Gear Geometry 47
7.2 Landing Gear Stroke 48
7.3 Oleo Shock Absorber 50

8. IV
LIST OF SYMBOLS & ABBREVIATIONS
A. R - Aspect Ratio
b - Wing span(m)
C - Chord of the Aerofoil (m)
Croot - Chord at Root (m)
Ctip - Chord at Tip (m)
Cd - Drag Co-efficient
Cdo - Zero lift Drag co-efficient
CP
- Specific fuel consumption (lbs /
hp / hr)
CL - Lift Co-efficient
D - Drag(N)
E - Endurance (hr)
e - Oswald efficiency factor
L - Lift (N)
(L/D) Loiter - Lift-to-drag ratio at loiter
(L/D) Cruise - Lift-to-drag ratio at cruise
M - Mach number of aircraft
Mff - Mission fuel fraction
R - Range (km)
Re - Reynolds number
s - Wing area (m2
)
Sref - Reference surface area
Swet - Wetted surface area
Sa - Approach distance (m)
Sf - Flare distance (m)
Sfr - Freeroll distance (m)
S.C - Service ceiling
A.C - Absolute ceiling

9. V
T - Thrust (N)
Tcruise - Thrust at cruise (N)
Ttake-off - Thrust at take-off (N)
(T/W) Loiter - The thrust-to-weight ratio at Loiter
(T/W) Cruise - The thrust-to-weight ratio at cruise
(T/W) Take-off - The thrust-to-weight ratio at take-off
vCruise - velocity at cruise (m/s)
vStall - velocity at stall (m/s)
vt - Velocity at touch down (m/s)
WCrew - Crew weight (kg)
Wempty - Empty weight of the aircraft (kg)
Wfuel - Weight of fuel (kg)
Wpayload - Payload of the aircraft (kg)
W0 - Overall weight (kg)
W/S - Wing loading (kg/m2
)
ρ - Density of air (kg/m3
)
μ - Dynamic viscosity (Ns/m2
)
λ - Tapered ratio
R/C - Rate of Climb
ηs
ηt
St
Vvertical
- Shock absorption efficiency of oleo
- Shock absorption efficiency of tire
- Maximum allowable tire deflection
- Vertical velocity

10. 1
CHAPTER 1
SUMMARY FROM AIRCRAFT DESIGN PROJECT – I
1.1 PURPOSE OF THE AIRCRAFT
Fighter Aircrafts are the aircrafts used only for the defense purpose of the
country. There are different types of fighter aircrafts depending on the mission to
accomplish some of them are Interceptor, Bomber, Dogfight, reconnaissance etc. The
present time fighters are of 4th, 4.5th and 5th generation fighter Aircrafts.
The Specialty of them is Stealth, Super cruise, STOL, Multirole etc. The
fifth-generation fighters are completely stealth fighters capable of operating at
different atmospheric condition. Even though there are no bombers in the fifth
generation the multirole fighters it acts as a bomber. The stealth Aircraft is an ideal
Aircraft for reconnaissance.
1.2 MISSION PROFILE
Figure 1.1 Mission Profile for fighter aircraft

11. 2
DESCRIPTION:
0 - 1 - Engine Start & Warm up 6 - 7 - Descent
1 – 2 - Taxing 7 - 8 - Drop bombs
2 - 3 - Take off 8 - 9 - Strafe
3 - 4 - Climb 9 - 10 - Climb
4 - 5 - Cruise out 10 - 11 - Cruise in
5 - 6 - Loitering 11 - 12 - Descent
12 - 13 - Landing, Taxi, Shutdown

12. 3
1.3 FEATURES OF AIRCRAFT
1.3.1 ENGINE TYPE
 The preferable choice of engine is Pratt & Whitney F100 engine since the
engine thrust is 129 KN. It is a Single afterburning turbofan engine.
 Thrust required calculation 98.29 KN.
1.3.2 WING TYPE
Tapered wing with dihedral monoplane configuration mounted as a low wing.
1.3.3 AIRFOIL CHOSEN
1. Section used at the mean aerodynamic chord - GOE 490 AIRFOIL
2. The section used at the tip - CLARK X
3. The section used at the root - S2027.
1.3.4 FUSELAGE TYPE
A semi-monocoque fuselage has been constructed.
1.3.5 EMPENNAGE TYPE
Twin Tail Plane configuration is used because Twin tail design will give better
stability performance to the aircraft.
1.3.6 LANDING GEAR
Retractable Tri-cyclic landing gears is constructed.

13. 4
1.4 THREE VIEWS OF FIGHTER AIRCRAFT
Figure 1.2 Side view of Fighter Aircraft
Figure 1.3 Top view of Fighter Aircraft

14. 5
Figure 1.4 Front view of Fighter Aircraft
Figure 1.5 Isometric view of Fighter aircraft

15. 6
1.5 FINAL SPECIFICATIONS FROM ADP I
1.5.1 FINAL DESIGN PARAMETERS:
FLIGHT PARAMETER SI UNIT VALUE IMPEREAL
UNIT
VALUE
Length m 18 ft 59.05
Height m 5.1 ft 16.73
Wing Area m² 48 ft² 516.66
Wing Span (m) m 12.5 ft 41.01
Aspect Ratio 2.8 2.8
Max Take Off
Weight
Kg 16,000 lb 35,273.9
6
Empty weight Kg 9,000 lb 19,841
Payload Weight Kg 7,500 lb 16,534.67
Thrust to Weight Ratio 1.4 1.4
Max Speed Km/h 2,200 Mile/hr 1,367.01
Service Ceiling m 17,000 Miles 10.56
Range Km 2,250 Miles 1,398.08
Rate of Climb m/s 275 Miles/hr 615.157
Wing loading Kg/m² 440 lb/ft² 90.11
Dry Thrust KN 110 lbf 24,728.93
Afterburner Thrust KN 130 lbf 29,225.16
Table 1.1 Final design parameters

16. 7
1.5.2 WEIGHT PARAMETERS
PARAMETERS SI UNIT (Kg) IMPERIAL UNIT (lbs)
Take-off Weight (WTO ) 16,000 35,273.96
Fuel Weight (WF ) 932.79 2056.46
Empty Weight (WE ) 8041.34 17728.13
Payload Weight (Wpayload ) 7,500 16,534.67
Table 1.2 Weight parameters
1.5.3 LIFT AND DRAG CALCULATION
CONDITION LIFT (N) DRAG (N)
TAKE-OFF 159362 36453
CRUISE 159365 6143.36
LANDING 159515 42796
Table 1.3 Lift and drag parameters
1.5.4 WING PARAMETERS
S.NO DESIGN CHARACTERISTICS VALUES
1 Wing loading (Kg/𝐦𝟐
) 440
2 Wing Area S (𝐦𝟐
) 36.36
3 Aspect Ratio 2.8
4 Span b (m) 10.08
5 Taper ratio (λ) 0.5
6 Root Chord (m) 3.6
7 Tip chord (m) 1.8
8 Mean chord (𝑪) 2.8
Table 1.4 wing design parameters

17. 8
1.5.5 PERFORMANCE CALCULATION
PARAMETER VALUE
THRUST REQUIRED 14.08 KN
THRUST AVAILABLE 98.29 KN
POWER REQUIRED 8408.57 KW
POWER AVAILABLE 54494.5 KW
RATE OF CLIMB 293.71 m/sec
RATE OF SINK 57.84 m/sec
TAKE – OFF DISTANCE 2680.15 m
LANDING DISTANCE 1618.99 m
Table 1.5 Performance parameters

18. 9
CHAPTER 2
V-n DIAGRAM
2.1 INTRODUCTION:
Airplanes may be subjected to a variety of loading conditions in flight. The
structural design of the aircraft involves the estimation of the various loads on the aircraft
structure and designing the airframe to carry all these loads, providing enough safety
factors, considering the fact that the aircraft under design is a commercial transport
airplane. As it is obviously impossible to investigate every loading condition that the
aircraft may encounter, it becomes necessary to select a few conditions such that each one
of these conditions will be critical for some structural member of the airplane.
2.2 Velocity –Load Factor (V-n) diagram:
The control of weight in aircraft design is of extreme importance. Increases in
weight require stronger structures to support them, which in turn lead to further increases
in weight and so on. Excess of structural weight mean lesser amounts of payload, thereby
affecting the economic viability of the aircraft. The aircraft designer is therefore
constantly seeking to pare his aircraft’s weight to the minimum compatible with safety.
However, to ensure general minimum standards of strength and safety, airworthiness
regulations (Av.P.970 and BCAR) lay down several factors which the primary structure
of the aircraft must satisfy. These are the
 Limit load, which is the maximum load that the aircraft is expected to experience
in normal operation.
 Proof load, which is the product of the limit load and the proof factor (1.0- 1.25),
and
 Ultimate load, which is the product of the limit load and the ultimate factor
(usually 1.5). The aircraft’s structure must withstand the proof 39 load without
detrimental distortion and should not fail until the ultimate load has been
achieved.

19. 10
The basic strength and fight performance limits for a particular aircraft
are selected by the airworthiness authorities and are contained in the flight envelope or
V-n diagram.
LOAD FACTOR
The load to the aircraft on the ground is naturally produced by the gravity (i.e., 1 times
g). But there are other sources of load to the aircraft during flight; one of which is the
acceleration load. This load is usually normalized through load factor (i.e., "n" times g).
In another word, aircraft load is expressed as a multiple of the standard acceleration due
to gravity (g = 9.81 m/sec2 = 32.17 ft/sec2)
n = L/W
In some instances of flight such as turn and pull-up, the aircraft must generate a lift force
such that it is more than weight. For instance, load factor in a pull-up from equation 9.86
can be re-written as:
n= a/g +1
Where "a" is the centrifugal acceleration (V2/R). As this acceleration increases; i.e.,
airspeed increases or radius of turn decreases; the load factor will increase too. For other
flight operations, similar expressions can be drawn. In some instances; especially for
missiles; this load factor may get as high as 30. As the table 2.2 illustrates, a low load
factor fighter may end up getting targeted by a high load factor missile.
Aircraft Type N(Positive) N(Negative)
General Aviation-normal 2.5 to 3.8 -1 to -1.5
General Aviation-utility 4.4 -1.8
General Aviation-Aerobatics 6 -3
Homebuilt 5 -2
Transport 3 to 4 -1 to -2
Strategic Bomber 3 -2
Tactical bomber 4 -2
Fighter 6.5 to 9 -3 to -6
Table 2.1 Typical Limit load factors for different aircrafts

20. 11
There are two types of V – n diagram for military airplanes :
 V–n maneuver diagram and
 V–n gust diagram
The below figure shows the Vn maneuver diagram
Figure 2.1 V-n Maneuver Diagram
There are four important speeds used in the V – n diagram
1 – g stall speed VS
Design maneuvering speed VA
Design cruise speed VC
Design diving speed VD

21. 12
2.3 GUST V-n DIAGRAM
DESCRIPTION:
Gust is a sudden, brief increase in the speed of the wind. Generally, winds are least gusty
over large water surfaces and most gusty over rough land and near high buildings. With
respect to aircraft turbulence, a sharp change in wind speed relative to the aircraft; a
sudden increase in airspeed due to fluctuations in the airflow, resulting in increased
structural stresses upon the aircraft.
Sharp-edged gust: is a wind gust that results in an instantaneous change in direction or
speed.
Derived gust velocity: is the maximum velocity of a sharp-edged gust that would produce
a given acceleration on a particular airplane flown in level flight at the design cruising
speed of the aircraft and at a given air density. As a result, a 25% increase is seen in lift
for a longitudinally disturbing gust. The effect of turbulence gust is to produce a short
time change in the effective angle of attack. These changes produce a variation in lift and
thereby load factor.
Effective gust velocity: The vertical component of the velocity of a sharp-edged gust that
would produce a given acceleration on a particular airplane flown in level flight at the
design cruising speed of the aircraft and at a given air density.
Below figure shows the model Vn gust diagram.
CONSTRUCTION OF GUST LOAD FACTOR LINES
The gust load factor lines are defined by the following equations
Nlim = 1 ±
( )
kg =
.
.
𝜇g = ̅
where,
kg = Gust alleviation factor
Ug = Derived gust velocity
VB = Design speed for maximum gust intensity

22. 13
Vc = Design cruise velocity
VD = Design diving velocity
𝐶̅ = Wing mean geometric chord = 2.8 m
W – Weight of aircraft = 16,000 kg
S - Area = 36.36 m
a - Overall lift curve slope
a =
Fig 2.2 Model V-n Gust Diagram

23. 14
CALCULATIONS:
Vs @ n= 1
Vs =
=
× × .
. × . × .
Vs= 50.27m/sec
Corner Speed,
Vo= √𝑛𝑚𝑎𝑥 . Vs
Vo= 128.164 m/sec
V-n =
× ×
. × . × .
V-n= 26.51 m/sec
Vc = 597.2 m/s
VD = 776.4 m/sec
𝛽 = √1 − 𝑀𝑐𝑟
= √1 − 1.91
𝛽 = 1.627

24. 15
Aspect Ratio = 2.8
SW = 36.36 𝑚
W = 16000 kg
Vc= 597.2 m/sec
a =
× . × .
( ( . )( . )^ (
( . ^ )
)
= 1.769
𝜇𝑔 =
×
. × . × .
𝜇𝑔 = 138.19
kg =
. ( . )
.
kg = 0.8737
Vg at sea level = 17.07 m/s
ng = 1±∆ 𝑛𝑔
= 1±
. . . . .
×
ng = 1±0.03672Vc
For VD,
Vg = 8.54
ng = 1±∆ 𝑛𝑔
= 1±
ng = 1± 0.01837VD

25. 16
Calculated Vn Diagram For our Fighter Aircraft is:
Calculate values are
Maximum Positive Load factor = 6.5
Corner Velocity = 128.16m/sec
Stall Speed = 50.27 m/sec
Cruise Speed = 597.2 m/sec
Dive Speed = 776.4 m/sec
Fig 2.3 Vn Diagram for our fighter aircraft

26. 17
Calculated Vn-Gust Diagram For our Fighter Aircraft is:
Calculated values are
𝜇𝑔 = 138.19
kg = 0.8737
ng = 1±0.03672Vc
ng = 1± 0.01837VD
Dive speed = 776.4 m/sec
Fig 2.4 Vn Gust Diagram for Our fighter aircraft
CONCLUSION
Calculations and Construction of Vn Diagram and Vn Gust Diagram has been done
using MATLAB.

27. 18
CHAPTER 3
SCHRENK’S CURVE
3.1 WING DESCRIPTION
Lift distribution over a wing can be determined using Schrenk’s method. The
equation for the lift distribution is formed by taking semi span on the X axis and the lift
distribution along Y axis. The Schrenk’s curve is used to approximate the lift distribution
along the span of the wing.
Schrenk’s Curve is given by
Y =
𝒀𝟏 𝒀𝟐
𝟐
Where,
y1 is Linear Variation of lift along semi wing span also named as L1,
y2 is Elliptic Lift Distribution along the wing span also named as L2.
According to Schrenk, the actual lift distribution on an aircraft wing is the average of
two types of lift distributions:
 LINEAR LIFT DISTRIBUTION
 ELLIPTICAL LIFT DISTRIBUTION

28. 19
3.1.1 LINEAR LIFT DISTRIBUTION
Figure 3.1 Typical linear lift distribution
Lift at root:
LRoot = =
. × . × × .
= 14433.86 (N/m)
LRoot = 14433.86 N/m
Where,
ρ = Density at sea level = 1.225 Kg/𝑚
V = Velocity = 57.21 m/s
CL = coefficient of lift = 2
Croot = 3.6 m
Ctip = 1.8 m

29. 20
Lift at tip
Ltip = =
. × . × × .
= 7,216.93 (N/m)
Ltip = 7,216.93 N/m
Equation of linear lift distribution for port wing
𝑌1 = 𝑚𝑥 + c
m = (7216.93 – 14433.86)/(5.04 – 0) = -1431.93
𝑌1 = -1431.93𝑥 + 14433.86
X 0 1 2 3 4 5 5.04
Y 14433.86 13001.93 11,570 10138.07 8706.14 7274.21 7216.93

30. 21
DIAGRAM
Figure 3.2 Linear Lift Distribution

31. 22
3.1.2 ELLIPTICAL LIFT DISTRIBUTION
Figure 3.3 Typical elliptical lift distribution
Twice the area under the curve or line will give the lift which will be
required to overcome weight.
Considering an elliptic lift distribution, we get
L = n.W
A =
𝝅𝒂𝒃
𝟒
Where
b- is Actual lift at root
a- is wing semi span
Lift at tip
b = =
.
b = 20139.78 N

32. 23
EQUATION OF ELLIPTIC LIFT DISTRIBUTION:
Y2 = √𝑎 − 𝑥
Y2 =
× .
.
5.04
2
− 𝑥2
Y2 = 7991.98√25.4016 − 𝑥
x 0 1 2 3 4 5 5.04
Y 40279.58 39478.76 36972.38 32366.63 24505.03 5064.67 0
DIAGRAM
Figure 3.4 Elliptic Lift Distribution

33. 24
3.1.3 SCHRENK’S CURVE
CONSTRUCTION OF SCHRENK’S CURVE:
Schrenk’s Curve is given by
Y =
Y =
. . . √ .
x 0 1 2 3 4 5 5.04
Y 27356.71 26,240.34 24271.19 21252.35 16605.58 6169.44 3608.47
DIAGRAM
Figure 3.5 Schrenk’s Curve

34. 25
CHAPTER 4
WING LOAD ESTIMATION
4.1 SELF WEIGHT DISTRIBUTION
Weight distribution is the apportioning of weight within a vehicle, especially cars,
airplanes and trains. Typically, it is written in the form x/y, where x is the percentage of
weight is the front, and y is the percentage in the back.
In a vehicle which relies on gravity in same way, weight distribution directly
affects a variety of vehicle characteristics, including handling, acceleration, traction, and
component life. For this reason, weight distribution varies with the vehicle’s intended
usage. For example, a drag car maximize traction at the rear axle while countering the
reactionary pitch-up torque. It generates this counter-torque by placing a small amount of
counterweight at a great distance forward of the rear axle.
In the airline industry, load balancing is used to evenly distribute the weight of
passenger cargo, and fuel throughout an aircraft, so as to keep the aircraft’s center of
gravity close to its center of pressure to avoid losing pitch control. In military transport
aircraft, it is common to have a loadmaster as a part of the crew; their responsibilities
include calculating accurate load information for center of gravity calculation, and
ensuring cargo is properly secured to prevent its shifting.
In large aircraft and ships, multiple fuel tanks and pumps are often used, so that
as fuel is consumed, the remaining fuel can be positioned to keep the vehicle balanced,
and to reduce stability problems associated with the free surface effect.
CALCULATION:
Y = k (m − a)
ρ =
W= ρgv

35. 26
Where,
Material used = Aluminum
Density of material, 𝜌 = 2700 kg/m
y = −Wtip − k(𝒙 −
𝒃
𝟐
)𝟐
Where,
b/2 = half span = 5.04
At x = 0; y = -Wroot
K =(( )
( / ) )
Equation becomes,
y = −Wtip - (( )
( / )
)(𝑥 − )
From ADP – I,
The section used at the tip - CLARK X
The section used at the root - S2027
At root,
Vroot = Croot x Troot x 0.2
= 3.6 x 0.02826 x 0.2
= 0.02035 𝑚
Vroot = 0.02035 𝒎𝟑
Wroot = 𝜌gVroot
= 2700 x 9.81 x 0.02035
=539.01 N
Wroot = 539.01N

36. 27
At tip,
Vtip = Ctip x Ttip x 0.2
= 1.8 x 0.0105 x 0.2
= 0.00378 m
Vtip = 0.00378 𝐦𝟑
Wtip = 𝜌gVtip
=2700 x 9.81 x 0.00378
= 100.12086 N
Wtip = 100.12086 N
K =(
( )
( / )
) = (
( . . )
( . )
)
K = 17.278
y = −Wtip − k(𝑥 − )
y = −100.12086 – 17.278 (𝑥 − 5.04)
For different x values, we get
x 0 1 2 3 4 5
Y -539.009 -382.125 -259.797 -172.024 -118.808 -100.148

37. 28
DIAGRAM
Figure 4.1 Self Weight Distribution

38. 29
4.2 FUEL WEIGHT DISTRIBUTION:
This design has fuel in the wing so we have to consider the weight of the
fuel in one wing.
From similar trapezoid,
ABCD + EFGH
Figure 4.2 Fuel tank dimensions
Take b = half span
=
( . )
l1 =
.
Croot = (
5.04−0.2
5.04
) 3.6
l1 = 3.457 m
From similar trapezoids,
ABCD+ GHCD
=
( . )
l2 =(
( . )
) Croot

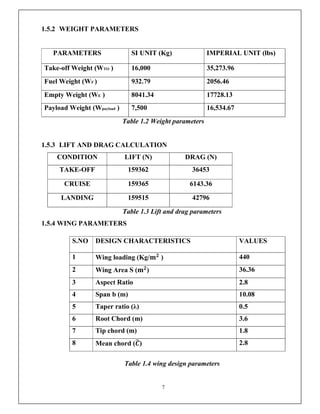
39. 30
Volume of the fuel tank
Vfuel = Area * t
= {Area rectangle + 2(Area triangle)}*t
= {(h*l2) +2[ h
( )
]}*t
={(h*l2) + [ h (l1 − l2)]}*t
={(h*(
( . )
) Croot ) + [ h (
( . ) ( . )
)]}*t
={((
( . )
) Croot ) +[
(Croot b−0.2−b−h−0.2 )
b
]}h*t
={(b − h − 0.2)+[0.5(b-0.2-b+h+0.2)]} h*t
= {(b − h − 0.2)+0.5h} h*t
Vfuel =
root
h ∗ t (b − − 0.2)
Density of fuel, 𝜌𝑓𝑢𝑒𝑙 =
Vfuel = (
𝑚
ρ
) fuel
Where,
Mass of fuel, m = 932.79 kg
Density of fuel, 𝜌 = 801 kg/m
Vfuel =
.
=1.16 m
Vfuel = 1.16 𝐦𝟑
Solving h,
Vfuel =
root
h ∗ t (b − − 0.2)
Where,
Vfuel = 1.16 m
Half span, b = 5.04 m
Croot = 3.6 m

40. 31
t= =
. .
= 0.01938 m
Now,
1.16 =
.
.
× ℎ × 0.01938(5.04 − − 0.2)
1.16=0.71429× ℎ × (0.09767 − 0.00969ℎ − 0.003876)
h= 2.23 m
l2 =(
( . )
) Croot
l2 =(
( . . . )
.
) 3.6 = 1.86 m
l2 = 1.86 m
W1 = (0.1*l1*tm) *𝜌*g
= (0.1*3.457*0.01938)*801*9.81
= 52.64
W1 = 52.64 N
W2 = (0.1*l2*tm) *𝜌*g
= (0.1*1.86* 0.01938) * 801*9.81
= 28.32
W2 = 28.32 N
Slope of fuel weight:
Y = mx + c
m = (28.32 – 52.64)/(2.43 – 0.2) = -10.9
Y = -10.9x +54.81

41. 32
DIAGRAM
Figure 4.3 Fuel Weight Distribution

42. 33
4.3 OVERALL LOAD ACTING ON THE WING STRUCTURE
Wing Span
(m)
Linear (N) Elliptical
(N)
Schrenk’s
(N)
Self-Weight
(N)
Fuel Weight
(N)
0 14433.86 40279.58 27356.71 -539.009 -54.81
1 13001.93 39478.76 26240.34 -382.125 -43.95
2 11570 36972.38 24271.19 -259.797 -33.09
3 10138.07 32366.63 21252.35 -172.024 -22.23
4 8706.14 24505.03 16605.58 -118.808 -11.37
5 7274.21 5064.67 6169.44 -100.148 -0.51
Table 4.1 Overall Weight Acting on the Wing Structure
DIAGRAM
Figure 4.4 Overall Weight Distribution

43. 34
CHAPTER 5
SHEAR FORCE AND BENDING MOMENT DIAGRAM
5.1 DESCRIPTION
The solution methods which follow Euler’s beam bending theory
(σ/y=M/I=E/R) use the bending moment values to determine the stresses developed at a
particular section of the beam due to the combination of aerodynamic and structural loads
in the transverse direction. Most engineering solution methods for structural mechanics
problems (both exact and approximate methods) use the shear force and bending moment
equations to determine the deflection and slope at a particular section of the beam.
Therefore, these equations are to be obtained as analytical expressions in terms of span
wise location. The bending moment produced here is about the longitudinal (x) axis.
5.2 LOADS ACTING ON WING:
As both the wings are symmetric, let us consider the starboard wing at first. There are
three primary loads acting on a wing structure in transverse direction which can cause
considerable shear forces and bending moments on it. They are as follows:
 Linear Lift distribution of the wing
 Elliptical Lift distribution of the wing
 Self-weight of the wing
 Weight of the fuel in the wing
5.3 TO FIND CENTEROID AND STRUCTURAL WEIGHT
Lift Force given by Schrenk’s Curve:
Y =
Y =
−1431.93x + 14433.86 +7991.98√25.4016−𝑥2

44. 35
LINEAR LIFT DISTRIBUTION (TRAPEZIUM):
𝑌1 = - 1431.93 𝑥 + 14433.86
Triangle area, A1 = ½ bh
= ½ * 5.04*(14433.86 - 7216.93)
A1 = 18186.66
Rectangle area, A2 = l*b
= 7216.93* 5.04
A2=36373.32
A1+ A2 = 18186.66+3637.32
A1+ A2 = 54559.98 N
x1 = 1/3 𝑎 = 1/3 ∗ 5.04 = 1.68
x2 = 𝑎/2 =
.
= 2.52
Centroid (Y) = =
( . ∗ . ) ( . ∗ . )
.
Y= 2.239 m

45. 36
ELLIPTIC LIFT DISTRIBUTION (QUARTER ELLIPSE) :
𝑌2 = 7991.98 √25.4016 − 𝑥
For Elliptical,
a = 5.04
b = 40279.58
Area of ellipse = =
. × . × .
A = 159362.13 N
Centroid (Y) = =
× .
× .
= 2.14
Y = 2.14 m

46. 37
SELF-WEIGHT OF WING (𝒀𝟑):
Y3 = -100.12 – 17.278 (𝑥 − 5.04)
For Self -Weight
b= 5.04
h= 539.009
Area = bh = × 5.04 × 539.009
A = 905. 53 N
Centroid (Y) = =
× .
Y = 1.89 m

47. 38
FUEL WEIGHT:
Slope of fuel weight:
Y = mx + c
Y = -10.86x+54.81
For fuel weight,
a = 1.23
b1= 13.366
b2 = 39.275
Triangle area, A1 = b1×a = × 1.23 ×13.366
A1 = 8.4009 N
Rectangle area, A2 = a*b2 = 39.274 × 1.23
A2 = 48.30 N
A1 + A2 = 8.4009 + 48.30 = 56.70792
x1 = = 1.23 * 0.5 = 0.615
x2 = = 1.23 *0.5 = 0.14
Centroid (Y) = =
( . × . ) ( . × . )
.
Y= 0.585 m

48. 39
Curve/ Component Area enclosed/Structural weight (N) Centroid (from wing
root) (m)
Y1 (linear) 54559.98 2.239
Y2 (Elliptical) 159362.13 2.14
Wing 905.53 1.89
Fuel 56.7079 0.585
Table 5.1 Distance and force of each component in wing

49. 40
5.4 REACTION FORCE AND BENDING MOMENT CALCULATIONS:
V = 0,
Then,
54559.98 + 159362.13 – 905.53 – 56.708 - VA = 0
VA = - 212959.87
M = 0,
Then,
(54559.98 *2.239) + (159362.13 *2.14) - (905.53 *1.89) - (56.708 *0.585) - MA = 0
MA = 461450.1275

50. 41
5.4.1 SHEAR FORCE:
𝑆𝐹𝐵𝐶 = ∫(( ) – y3) dx – VA
By using the corresponding values of x in appropriate equations we get the
plot of shear force.
Figure 5.1 Shear force diagram

51. 42
5.4.2 BENDING MOMENT
𝐵𝑀𝐵C = ∬( + 𝑦3 − 𝑉𝐴 ) d𝑥 + MA
By using the corresponding values of x in appropriate equations we get the plot of
bending moment.
DIAGRAM
Figure 5.2 Bending moment diagram

52. 43
CHAPTER 6
TYRE ANALYSIS
6.1 INTRODUCTION
The wheel is a circular metal object upon which the rubber tire is mounted.
The brake inside the wheel slows the aircraft by increasing the rolling friction. However,
the term wheel is frequently mean entire brake/wheel/tire assembly. The tires are sized to
carry the weight of the aircraft typically; the main tires carry about 90% of MTOW. Nose
tires carry only about 0% of the static load but experience higher dynamic loads during
landing.
For early conceptual designs, the engineer can copy the tire size of similar
design or follow a statistical approach. The table provides the equations for estimating
main tire size. These calculated values are for diameter and width and should be increased
by 30% is to operate from rough unpaved runways. Nose tires can be assumed to be about
60 – 100% the size of the main tires.
Figure 6.1 Tire contact area

53. 44
TYPE DIAMETER WIDTH
A B A B
General Aviation 1.51 0.349 0.7150 0.312
Business twin 2.69 0.251 1.170 0.216
Transport / Bomber 1.63 0.315 0.1043 0.480
Jet Fighter /Trainer 1.59 0.302 0.0980 0.467
Table 6.1 Statistical Tire Sizing
SURFACE MAXIMUM PRESSURE, PSI
Aircraft carrier 200+
Major Military Airfield 200
Major Civil Airfield 120
Tarmac runway, good foundation 70-90
Tarmac runway, poor foundation 50-70
Temporary metal runway 50-70
Dry grass on hard soil 45-60
Dry grass on soft soil 30-45
Hard packed sand 40-60
Soft sand 25-35
Table 6.2 Recommended Tire Pressure
6.2 SELECTION PROCEDURE
The number of tires required for a given aircraft design gross weight is largely determined
by the floatation characteristics. The primary consideration is the load-carrying capacity
of the tire during the speed regime normally applicable for landing or takeoff cycles. In
addition, the number of ply and type of construction, which determine the weight of the
wire and its operational life, is important from an economic standpoint.

54. 45
Other considerations include the inflation pressure of the tire and the size of the wheel.
The former must be chosen in accordance with the bearing capacity of the airfield from
which the aircraft is designed to operate from, whereas the latter must have sufficient
space to house the brake assembly. The choice of the main wheel tires is made on the
basis of the static loading case. The total main gear load is calculated assuming that the
aircraft is taxing at low speed without braking. The choice of the nose wheel tires is based
on the nose wheel load during braking at maximum effort, i.e., the steady braked load.
6.2.1 CALCULATION
Maximum take-off weight of the aircraft (Wmtow) = 16000 kg = 35273.96 lbs
Weight of the main wheel (Ww) =
%
Ww =
. × .
Ww = 7936.641 lbs
MAIN WHEEL CONFIGURATION:
Main Wheel diameter/width = A(Ww)
Diameter: A = 1.59
B = 0.302
Main wheel diameter = 1.59*(7936.641) .
MTD = 23.94 inch
Width: A = 0.098
B = 0.467
Main wheel width = 0.098(7936.641) .
MTW = 6.49 inch

55. 46
NOSE WHEEL CONFIGURATION: (For Fighter Aircraft)
Nose wheel diameter = 0.6 to 0.9 * Main Tire Diameter (MTD)
= 0.9 * 23.94
NTD = 21.546 inch
Nose wheel width = 0.6 to 0.9 * Main Tire Width (MTW)
= 0.9 * 6.49
NTW = 5.841 inch

56. 47
CHAPTER 7
LANDING GEAR ANALYSIS
7.1 INTRODUCTION
Landing gear is the undercarriage of an aircraft or spacecraft and may be used
for either takeoff or landing. Of the many internal components that must be defined in an
aircraft layout, the landing gear will usually cause the most trouble. Landing gear must
be placed in the correct down position for landing and must somehow retract into the
aircraft without chopping up the structure.
Figure 7.1 Tricycle Landing gear geometry

57. 48
7.2 SHOCK ABSORBER
The landing gear is used to absorb the shock of the landing and smooth out the
ride. The tire themselves will be absorbing some shock by deflecting when bump is
encountered. Sailplane and a few homebuilt airplanes have built with rigid axles, relying
solely upon the tires for shock absorbing.
The solid spring gear is used in many general aviation aircraft. The solid
spring is as simple as possible but is slightly heavier than other types of gear. Note that
the solid spring gear deflects with some lateral motion instead of straight up and down.
This lateral motion tends to scrub the tires sideways against the runways, wearing them
out. The solid spring has no damping other than this scrubbing action. The aircraft thus
lends to bounce a lot, much like a car with bad shock-absorbers.
Figure 7.2 Landing gear stroke

58. 49
7.3 STROKE DETERMINATION
The required deflection of the shock absorbing system depends upon the vertical
velocity at touch down, the shock absorbing material, and the amount of the wing will
available after touchdown. As a rough rule of thumb, the stroke in inches approximately
equals the vertical velocity at touchdown. The vertical at touchdown is established in
various specifications for different types of aircraft.
TYPE EFFICIENCY
Steel Leaf Spring 0.50
Steel Coil Spring 0.62
Air Spring 0.45
Rubber block 0.60
Rubber Bungee 0.58
Oleo pneumatic
 Fixed Orifice 0.65-0.80
 Metered Orifice 0.75-0.90
Tire 0.47
Table 7.1 Shock Absorber Efficiency
AIRCRAFT TYPE Ngear
Larger bomber 2.0-3
Commercial 2.7-3
General Aviation 3
Air Force Fighter 3.0-4
Navy Fighter 5.0-6
Table 7.2 Gear Load factor

59. 50
7.4 SELECTION OF SHOCK ABSORBER
OLEO SUSPENSION
An oleo struct is a pneumatic air – oil hydraulic shock absorber used on the landing gear
of most large aircraft and many smaller ones. This design cushions the impacts of landing
and damps out vertical oscillations.
Figure 7.3 Oleo Shock absorber
It is undesirable for an airplane to bounce on landing – it could to a loss of
control. The landing gear should not add to this tendency. A steel coil spring stores impact
energy from landing and then releases it. An oleo strut absorbs this energy, reducing
bounce.
As the strut compresses, the spring rate increases dramatically, because the air
is being compressed, while the viscosity of the oil dampens the rebound movement..

60. 51
CALCULATION:
Oleo suspension
Stroke distance, 𝑆 = − ηtst
Were,
𝜂𝑠 = Shock absorption efficiency of oleo = 0.90 (from the table)
𝜂𝑡 = Shock absorption efficiency of tire = 0.47
𝑆𝑡 = Maximum allowable tire deflection
𝑁𝑔𝑒𝑎𝑟 = 4 (from the table)
g = 386.22 inch/𝑠
𝑆𝑡 = Radius – Rolling radius
St= -
Where,
d = diameter of tire = 23.94 inch
𝑆𝑡 = 11.97 – 7.98
𝑆𝑡 = 3.99
Vvertical = 13 ft/sec = 156 inch/sec
S =
. ∗ . ∗
− 0.47 ∗ 3.99
= 6.67 inch
The stroke distance is 6.67 inches

61. 52
CHAPTER 8
CONCLUSION
 Hence multi role Aircraft has been designed with various performance and
aerodynamic parameters calculation, which can carry up to payload of 7500 kg i.e.,
armaments (Missiles, bombs, Guns etc.)
 Since the Engine will be equipped with Afterburner and Thrust Vectoring so it can
escape from combat field quickly and highly maneuverability. So, V-n diagram
was drawn to know the maneuverability limit of the aircraft which has 6.5 as
maximum load factor.
 Later gust V-n envelope was drawn by using the V-n diagram velocity and three
gust velocity was taken into account.
 The load distribution of wing in fighter aircraft using schrenk’s curve method was
found to be around 27356 N which is very sufficient for the fighter design
requirements. The self-weight and fuel tank capacity was found.
 It can have more combat radius because it has more fuel capacity with Drop tanks.
 The overall weight distribution gives the required data which are within the
estimated limits. Shear force and bending moment diagram for the wing structure
was adequate and within the structural limit.
 Tricycle Landing gear analysis was calculated with stroke distance as 6.67 inch
and the tyre size was estimated by using constant values of tyre.
 The diameter of main tyre was 21.546 inch which more enough for the fighter
aircraft to land.
 Finally, the aircraft design requirement of wing structure, aerodynamic forces are
calculated successfully.

62. 53
REFERENCE
1. Ajay Kumar Kundu “Aircraft Design”, Cambridge University Press, ISBN -
9780511844652 (2010)
2. Daniel P. Raymer “Aircraft Design: A Conceptual Approach” American Institute
of Aeronautics and Astronautics, Inc. 2nd Edition ISBN 0-930403-51-7 (1992)
3. Egbert Torenbeek “Synthesis of subsonic Airplane design”, Delft University Press,
1st Edition ISBN - 9789024727247, 90-247-2724-3 (1982)
4. Gerard Frawley & Jim Thorn “International Directory of Military Aircraft”
Australian Aviation, ISBN – 187567120X, 9781875671205 (1996)
5. Ira H. Abbott & Albert E. von Doenhoff, “Theory of Wing Section – Including
summary of Airfoil data” Dover publications, ISBN - 0486605868 9780486605869
(1959)
6. Dr Jan Roskam “Airplane Design” Roskam aviation & engineering, Vol. 8 ISBN -
127-126-125-1 (2009)
7. John D. Anderson Jr. “Aircraft Performance and Design” WCB/McGrawHill,
ISBN - 9780070019713, 0-07-001971-1 (1999)
8. John D. Anderson Jr. “Fundamentals of Aerodynamics” McGraw-Hill Education,
6th Edition ISBN - 1259129918, 9781259129919 (2016)
9. John D. Anderson Jr. “Introduction to Flight” McGraw-Hill Education, ISBN
0073380245, 9780073380247 (2011)
10. Lloyd R. Jenkinson & James F. Marchman III “Aircraft Design Projects: for
engineering students”, Butterworth-Heinemann, ISBN - 0-75065772- 3 (2003)
11. Paul Jackson (Editor-in-Chief), “Jane’s All the World’s Aircraft”
12. Jane's Publishing, 95th Sub Edition, ISBN - 9780710626141, 0710626142 (2004)
13. William Green “The Observer’s World Aircraft Directory” Frederick Warne &
Co. Ltd, ISBN - 978-1125857120 (1961).