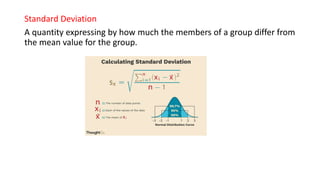
Errors in measurement can be categorized as static, systematic, or random. Static errors represent the difference between the true and measured values. Systematic errors are due to issues with instruments, environments, or observations. Random errors occur due to sudden changes and can only be reduced by taking multiple readings. There are various types of systematic errors such as instrumental errors from shortcomings, misuse, or loading effects, and environmental errors from temperature, pressure, or other external conditions. Statistical analysis methods like finding the average, deviations, standard deviation, and variance can help determine the most probable value from a set of measurements.

1. ERRORS IN MEASUREMENT

2. True Value
• It is not possible to determine the true value of a quantity by
experiment means. True value may be defined as the average value of
an infinite number of measured values when average deviation due to
various contributing factor will approach to zero.
Measured Value
• It may be defined as the approximated value of true value. It can be
found out by taking means of several measured readings during an
experiment, by applying suitable approximations on physical
conditions.

3. Static error is defined as the difference of the measured value and the true
value of the quantity.
 Mathematically we can write an expression of error as, dA = Am - At where,
dA is the static error ,
Am is measured value ,
and At is true value.
Limiting Errors or Guarantee Errors
The limits of these deviations from the specified value are defined as
limiting error.
Suppose there is a manufacturer who manufactures an ammeter, now he
should promise or declare that the error in the ammeter that he is selling is
not greater than the limit he sets. This limit of error is known as limiting
errors or guarantee error.
Aa=As±𝛿𝐴, where As is nominal value, 𝛿𝐴 is limiting error

4. Relative or Fractional limiting Error
It is error ∈ 𝑟 =
Aa−As
As
= defined as the ratio of the limiting error to the nominal (specified)
magnitude of the quantity. Mathematically we write as
∈ 𝑟 = 𝛿𝐴/ As = ∈ o / As,
∈ o = 𝛿𝐴 = ∈ 𝑟 As
In limiting errors the specified quantity As is taken as the true quantity,and
the quantity which has maximum deviation from Aa is taken as the
errourneous quantity.
𝛿𝐴 = Aa − As
Relative limiting
𝑎𝑐𝑡𝑢𝑎𝑙 𝑣𝑎𝑙𝑢𝑒 − 𝑛𝑜𝑚𝑖𝑛𝑎𝑙 𝑣𝑎𝑙𝑢𝑒
𝑛𝑜𝑚𝑖𝑛𝑎𝑙 𝑣𝑎𝑙𝑢𝑒

5. Known error
• When the error of a quantity or an instrument is known the effect of
this error, when combined with other errors, can be computed in a
manner similar to the combinations of limiting errors.
TYPES OF ERROR
1.Gross Error
2.Systematic Error
3.Random error

7. 1.Gross Error
• This category of errors includes all the human mistakes while reading,
recording and the readings. Mistakes in calculating the errors also
come under this category. For example while taking the reading from
the meter of the instrument he may read 21 as 31. All these types of
error are come under this category.
Gross errors can be avoided by using two suitable measures and they
are written below:
• A proper care should be taken in reading, recording the data. Also
calculation of error should be done accurately.
• By increasing the number of experimenters we can reduce the gross
errors. If each experimenter takes different reading at different
points, then by taking average of more readings we can reduce the
gross errors.

8. 2.Systematic Errors
• The systematic errors are mainly due to shortcomings of the
instrument and characteristics of the material used in the
instrument, such as defective or worn parts, ageing effects,
environmental effects,etc.
• A constant uniform deviation of the operation of an instrument is
known as a systematic error.
Three types of systematic errors are
2a.Instrumental Errors
2b.Environmental Errors
2c.Observational Errors

9. 2a.Instrumental Errors
Errors due to following reasons
(a)Short coming of Instruments:
Such types of errors are inbuilt in instruments because of their mechanical
structure. They may be due to manufacturing, calibration or operation of the
device. These errors may cause the error to read too low or too high.
For example – If the instrument uses the weak spring then it gives the high
value of measuring quantity. The error occurs in the instrument because of
the friction or hysteresis loss.
These errors can be avoided by the following methods
i)Selecting a proper instrument and planning the proper procedure for the
measurement
ii) Recognizing the effect of such errors and applying the proper correction
factors.
iii)Calibrating the instrument carefully against a standard.

10. 2a.Instrumental Errors
(b)Misuse of Instruments
The error occurs in the instrument because of the fault of the operator.
A good instrument used in an unintelligent way may give an enormous
result.
For example – the misuse of the instrument may cause the failure to
adjust the zero of instruments, poor initial adjustment, using lead to
too high resistance. These improper practices may not cause
permanent damage to the instrument, but all the same, they cause
errors.

11. 2a.Instrumental Errors
(c) Loading Effect
It is the most common type of error which is caused by the
instrument in measurement work. For example, when the voltmeter is
connected to the high resistance circuit it gives a misleading reading,
and when it is connected to the low resistance circuit, it gives the
dependable reading. This means the voltmeter has a loading effect on
the circuit.
The error caused by the loading effect can be overcome by using
the meters intelligently.

12. 2b.Environmental Errors
These errors are due to the external condition of the measuring devices.
Such types of errors mainly occur due to the effect of temperature, pressure,
humidity, dust, vibration or because of the magnetic or electrostatic field.
The corrective measures employed to eliminate or to reduce these
undesirable effects are
The arrangement should be made to keep the conditions as constant as
possible.
Using the equipment which is free from these effects.
By using the techniques which eliminate the effect of these disturbances.
By applying the computed corrections.

13. 2c.Observational Errors
• Such types of errors are due to the wrong observation of the reading.
There are many sources of observational error. For example, the
pointer of a voltmeter resets slightly above the surface of the scale.
Thus an error occurs(because of parallax) unless the line of vision of
the observer is exactly above the pointer. To minimize the parallax
error highly accurate meters are provided with mirrored scales.

14. 3.Random Errors
• The error which is caused by the sudden change in the atmospheric
condition, such type of error is called random error. These types of
error remain even after the removal of the systematic error. Hence
such type of error is also called residual error.
• The only way to reduce these errors is by increasing the number of
observations and using statistical methods to obtain best
approximation of the readings.

15. Statistical Analysis
• This method is used to find the most probable value from a group of
readings taken from a given experiment.
Average or arithmetic mean value
The average value is calculated by taking the sum of all of the
readings and dividing by the number of readings.

16. • Deviation from the average value
The deviation from the average value is a measure of how far each
measured value departs from the average value.
di = Xi -𝑋
Average Deviation
The mean or average deviation is a measure of how much the data is
dispersed or varies from the average value. It is calculated by adding all
the absolute values of the deviations of a set of measured values and
dividing this sum by the number of observations n.

17. Standard Deviation
A quantity expressing by how much the members of a group differ from
the mean value for the group.

18. Variance
• It is mean square deviation, which is the same as standard deviation
,except that square root is not extracted.