This document discusses dynamics and motion using normal-tangential and cylindrical coordinate systems. It includes:
1) Explanations of normal-tangential coordinates and how to set up and solve dynamics problems using these coordinates. Equations of motion are expressed in normal and tangential directions.
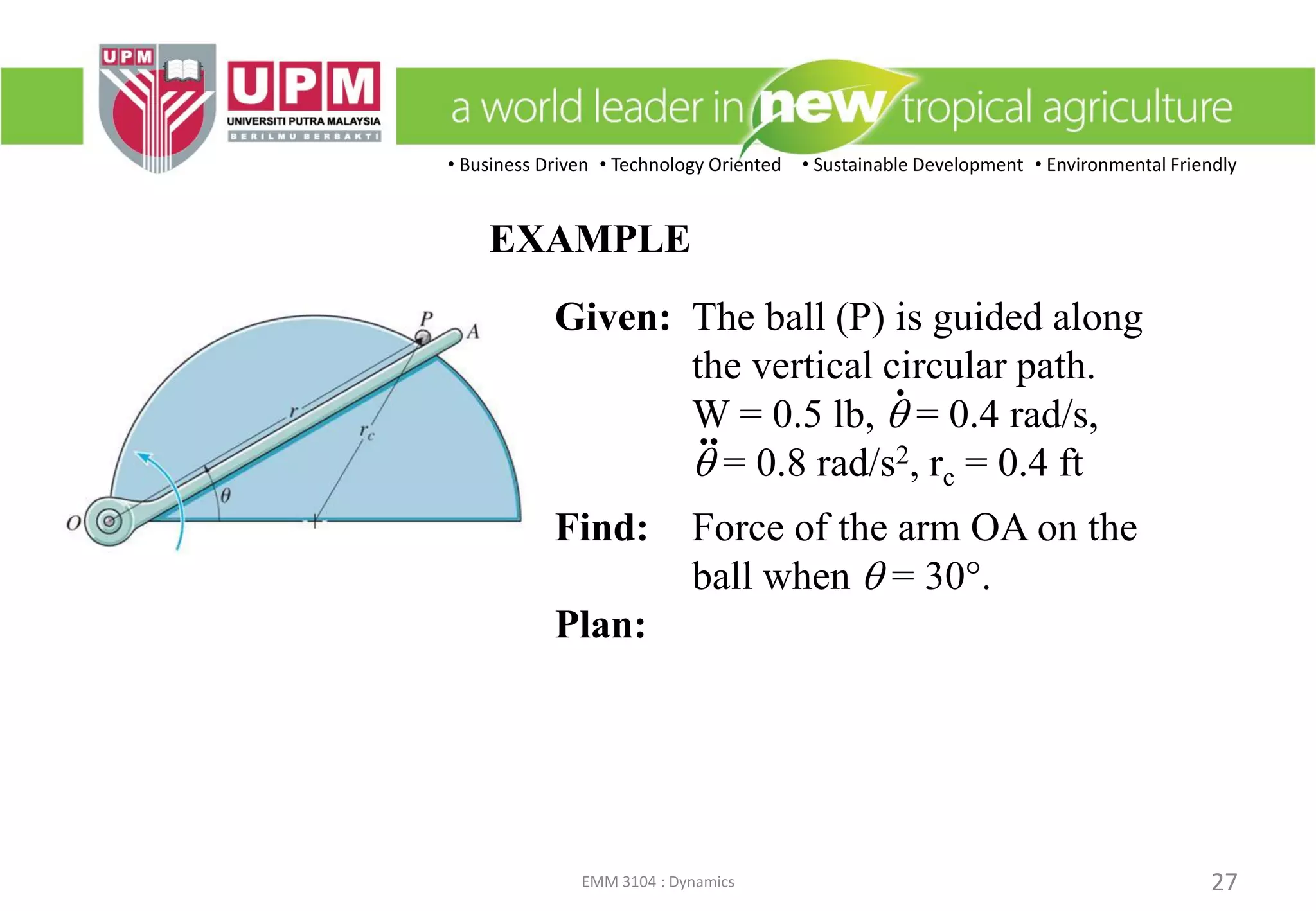
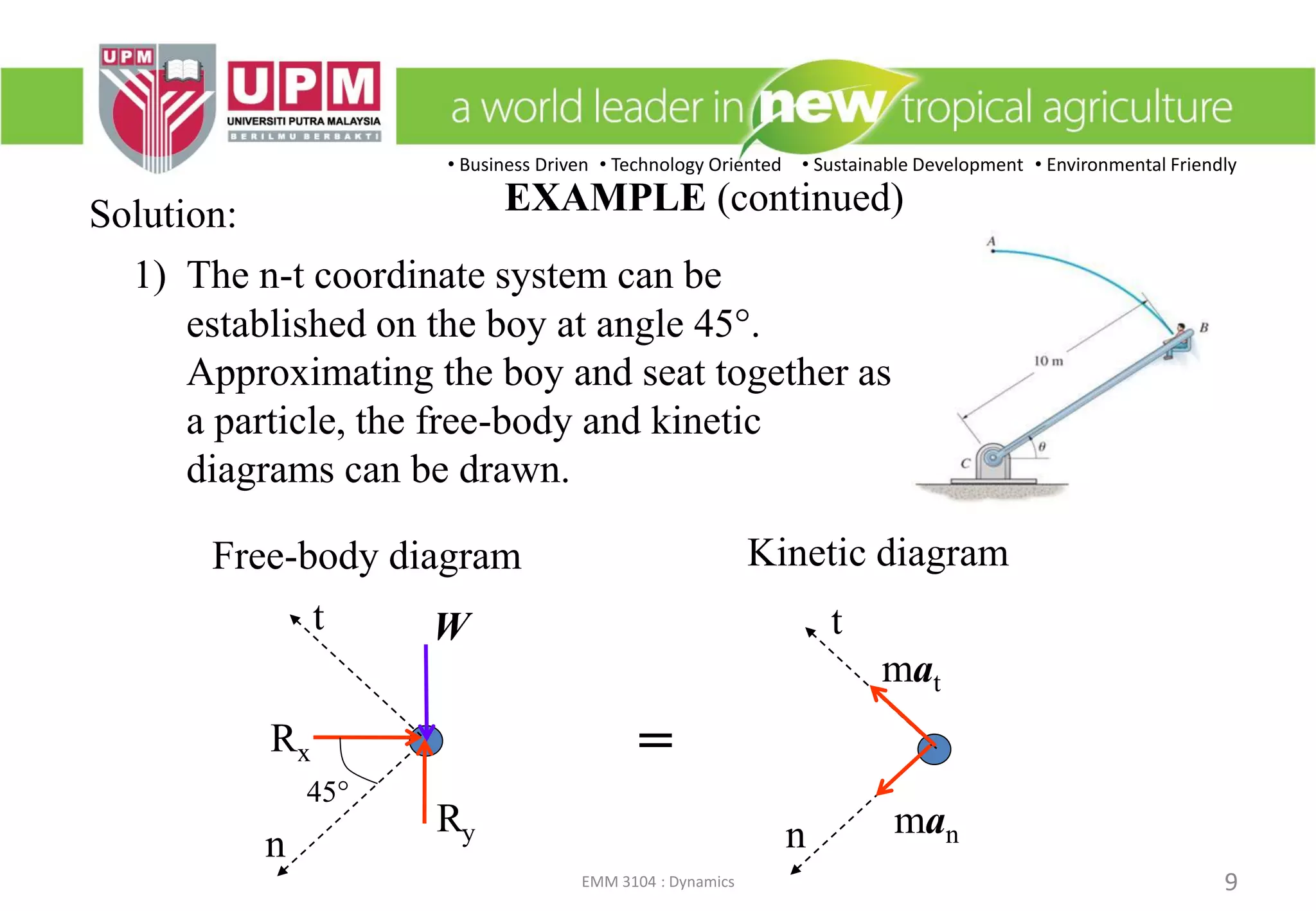
2) An example problem solving for reaction forces on a boy on a rotating amusement park ride using normal-tangential coordinates.
3) An introduction to cylindrical coordinates and how dynamics problems can be analyzed using these coordinates, with equilibrium equations expressed in r, θ, and z directions.
4) Details on determining tangential and normal forces when an object moves along a curved path defined by r=f(θ).





![• Business Driven • Technology Oriented • Sustainable Development • Environmental Friendly
EMM 3104 : Dynamics 6
NORMALAND TANGENTIAL ACCERLERATIONS
The tangential acceleration, at = dv/dt, represents the time rate of change in
the magnitude of the velocity. Depending on the direction of Ft, the
particle’s speed will either be increasing or decreasing.
The normal acceleration, an = v2/r, represents the time rate of change in the
direction of the velocity vector. Remember, an always acts toward the
path’s center of curvature. Thus, Fn will always be directed toward the
center of the path. For this reason, it is often referred to as centripetal force.
Recall, if the path of motion is defined as
y = f(x), the radius of curvature at any
point can be obtained from
r =
[1 + ( )2]3/2
dy
dx
d2y
dx2](https://image.slidesharecdn.com/emm3104chapter2w32-170417182200/75/Emm3104-chapter-2-part2-6-2048.jpg)






![• Business Driven • Technology Oriented • Sustainable Development • Environmental Friendly
EMM 3104 : Dynamics 14
3) Determine r by differentiating y = f(x) at x = 80 m:
Determine q from the slope of the curve at A:
y = 20(1 – x2/6400) => dy/dx = (–40) x / 6400
=> d2y/dx2 = (–40) / 6400
tan q = dy/dx
q = tan-1 (dy/dx) = tan-1 (-0.5) = 26.6°
x = 80 m
q
dy
dx
r = =
[1 + ( )2]3/2
dy
dx
d2y
dx2
[1 + (–0.5)2]3/2
0.00625x = 80 m
= 223.6 m
EXAMPLE (continued)](https://image.slidesharecdn.com/emm3104chapter2w32-170417182200/75/Emm3104-chapter-2-part2-14-2048.jpg)