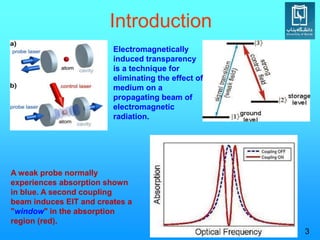
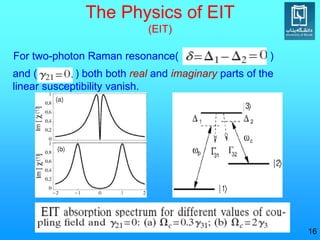
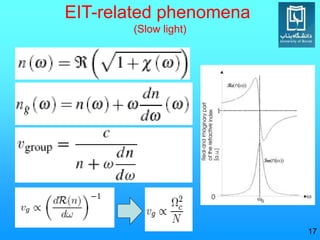
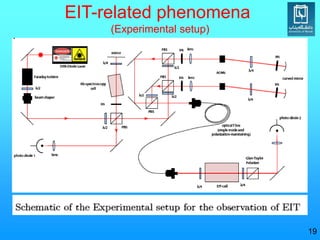
Electromagnetically induced transparency (EIT) is a quantum interference effect that can eliminate absorption of light in a medium. The effect was first observed in 1991 by Steve Harris. EIT occurs when a weak probe beam experiences reduced absorption due to destructive interference from a coupling beam. This creates a "window" of transparency. The physics of EIT involves coherent population trapping in a three-level atomic system using a probe and coupling laser. When the two-photon resonance condition is met, both the real and imaginary parts of the linear susceptibility vanish, resulting in EIT. EIT enables phenomena like slow light and light storage by significantly reducing the group velocity of light pulses.

1. Electromagnetically Induced Transparency
(EIT)
Presenter:
B. Younessi
Bonab University
1

2. Overview
• Introduction
• The history of EIT
• The Physics of EIT
• Some EIT-related phenomena
2

3. Introduction
3
A weak probe normally
experiences absorption shown
in blue. A second coupling
beam induces EIT and creates a
"window" in the absorption
region (red).
Electromagnetically
induced transparency
is a technique for
eliminating the effect of
medium on a
propagating beam of
electromagnetic
radiation.

4. The history of EIT
• The Physical effect that is the essence of EIT is called
coherent population trapping which was discovered in
1976 by Gerardo Alzetta and his coworkers at University
of Pisa in Italy
• Population trapping introduced and shown by Olga
Kocharovskaya and Yakov Khanin at the Kalinin
Leningrad Polytechnic institute in 1986
• EIT introduced in 1990 and experimentally observed in
1991 by Steve Harris
(Atac Imamoglu, K. Boller, Marlan Scully, … have also
played important roles in developing EIT)
4

5. The Physics of EIT
5

6. The Physics of EIT
(Physical and Optical Properties of Rubidium 87 )
From Quantum mechanics we have J= L+S
L: orbital angular momentum
S: spin angular momentum
The hyperfine structure is a result of the coupling of J with the total
nuclear angular momentum I. The total atomic angular momentum F is
then given by F=J+I
I: total nuclear angular momentum
The magnitude of F can take the values
For the 87Rb ground state, J = 1/2 and I = 3/2, so F = 1 or F = 2.
For the ground state in 87Rb, L = 0 and S = 1/2, so J = 1/2;
for the first excited state, L = 1, so J = 1/2 or J = 3/2 the L=0 L=1
(D line) transition is split into two components; the D1 line and
the D2 line
6

7. The Physics of EIT
(Physical and Optical Properties of Rubidium 87 )
7

8. The total Hamiltonian can be written as
After having introduced the dipole approximation as well as
the rotating wave approximation, the interaction Hamiltonian
can be represented in a rotating frame by
8
The Physics of EIT
(Static description of EIT)

9. The eigenvalues of the interaction Hamiltonian can be calculated to
9
The Physics of EIT
(Static description of EIT)
It is straightforward to verify that the corresponding eigenstates of
the interaction Hamiltonian are

10. 10
The Physics of EIT
(Static description of EIT)
If

11. The Physics of EIT
(The origin of EIT)
The ground state becomes
identical to the dark state from
which excitation cannot occur
11
This results in EIT

12. 12
The Physics of EIT
(Dynamic description of EIT)

13. 13
The Physics of EIT
(Dynamic description of EIT)
Master Equation
Polarization

14. 14
The Physics of EIT
(Density matrix solution)
By applying
perturbation theory
Off-diagonal
density-matrix
elements

15. 15
The Physics of EIT
(The linear susceptibility)

16. 16
The Physics of EIT
(EIT)
For two-photon Raman resonance( )
and ( ) both both real and imaginary parts of the
linear susceptibility vanish.

17. 17
EIT-related phenomena
(Slow light)

18. 18
EIT-related phenomena
(Light storage)

19. 19
EIT-related phenomena
(Experimental setup)

20. Thanks for your
attention and patience!
Any questions?