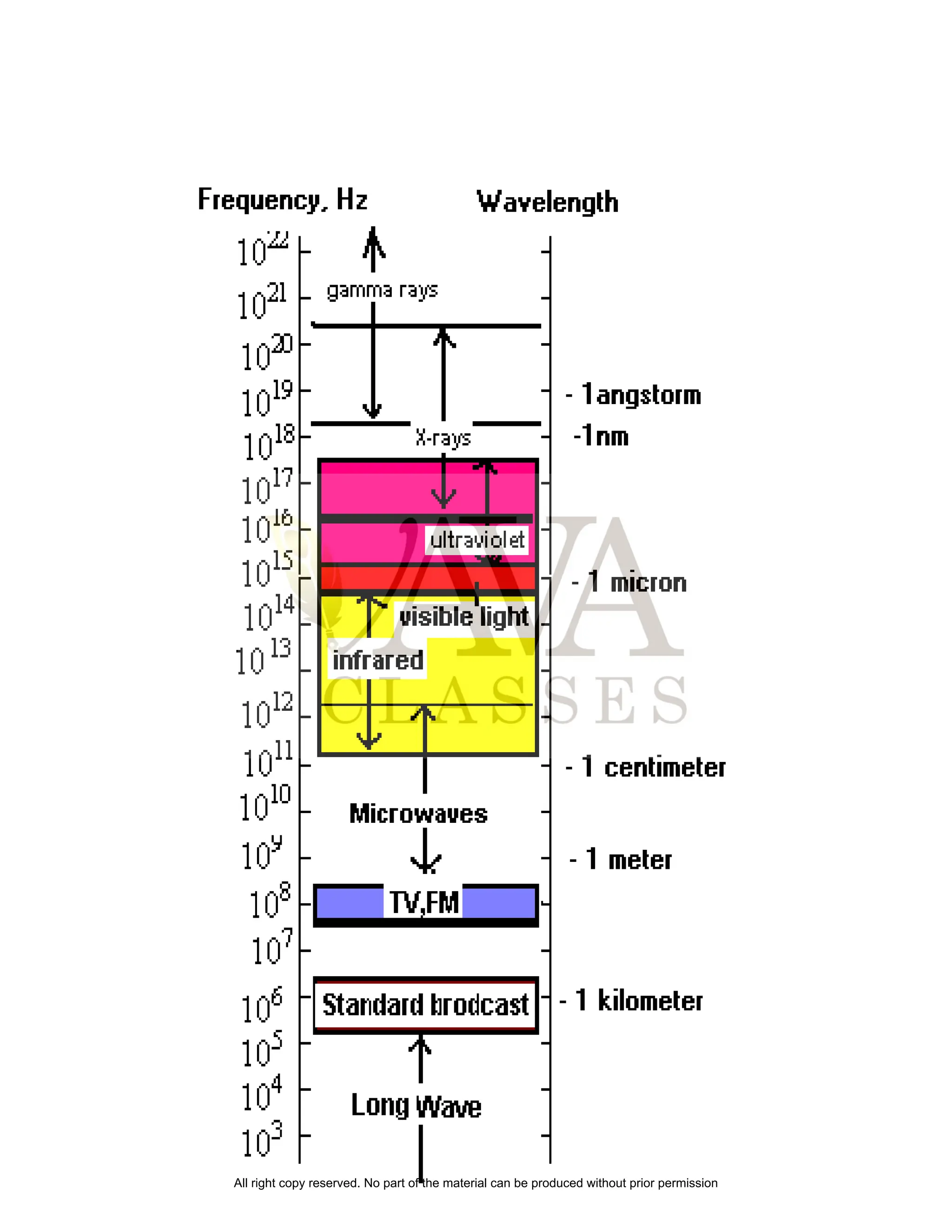
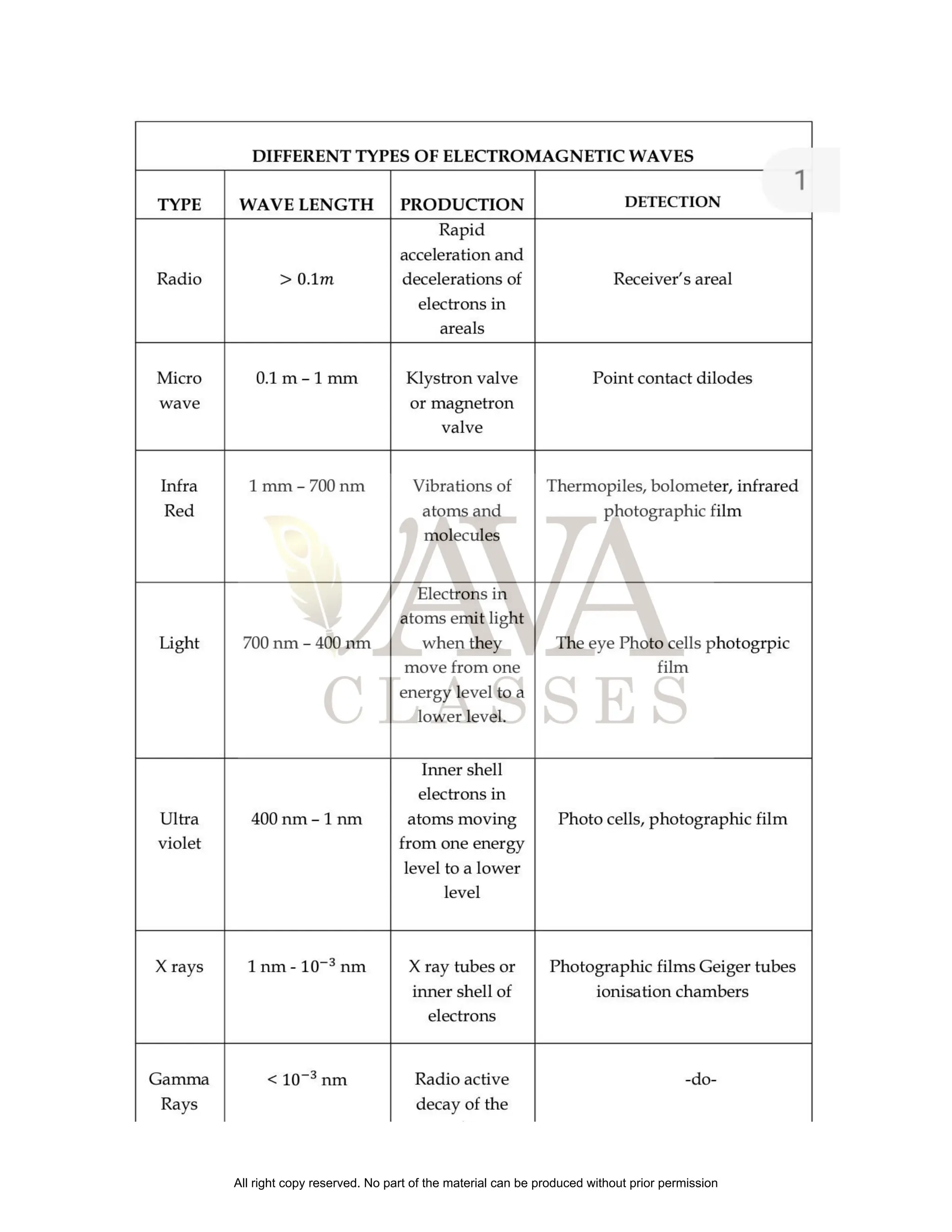
The document provides an overview of electromagnetic radiation (EMR), explaining its properties, types, and interactions with matter. It details the classification of EM waves in the electromagnetic spectrum, their corresponding frequencies, and applications such as communication, medical imaging, and heating. Additionally, the document discusses concepts like the displacement current, Ampere-Maxwell law, wave propagation, energy density, and intensity of EM waves.

1. STUDY MATERIAL E. M WAVE
INRODUCTION
In physics, electromagnetic radiation (EM radiation or EMR) refers to the waves
(or their quanta, photons) of the electromagnetic field, propagating (radiating)
through space, carrying electromagnetic radiant energy. It includes radio
waves, microwaves, infrared, (visible) light, ultraviolet, X-rays, and gamma rays.
Classically, electromagnetic radiation consists of electromagnetic
waves, which are synchronized oscillations of electric and magnetic fields. In a
vacuum, electromagnetic waves travel at the speed of light, commonly denoted c.
In homogeneous, isotropic media, the oscillations of the two fields are
perpendicular to each other and perpendicular to the direction of energy and
wave propagation, forming a transverse wave.
The wavefront of electromagnetic waves emitted from a point source (such as a
light bulb) is a sphere. The position of an electromagnetic wave within
the electromagnetic spectrum can be characterized by either its frequency of
oscillation or its wavelength. Electromagnetic waves of different frequency are
called by different names since they have different sources and effects on matter.
In order of increasing frequency and decreasing wavelength these are: radio
waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-
rays and gamma rays.
Electromagnetic waves are emitted by electrically charged particles undergoing
acceleration, and these waves can subsequently interact with other charged
particles, exerting force on them. EM waves
carry energy, momentum and angular momentum away from their source particle
and can impart those quantities to matter with which they interact.
Electromagnetic radiation is associated with those EM waves that are free to
propagate themselves ("radiate") without the continuing influence of the moving
charges that produced them, because they have achieved sufficient distance from
those charges. Thus, EMR is sometimes referred to as the far field. In this
language, the near field refers to EM fields near the charges and current that
All right copy reserved. No part of the material can be produced without prior permission

2. directly produced them, specifically electromagnetic induction and electrostatic
induction phenomena.
In quantum mechanics, an alternate way of viewing EMR is that it consists
of photons, uncharged elementary particles with zero rest mass which are
the quanta of the electromagnetic force, responsible for all electromagnetic
interactions.[6] Quantum electrodynamics is the theory of how EMR interacts with
matter on an atomic level.[7]
Quantum effects provide additional sources of EMR,
such as the transition of electrons to lower energy levels in an atom and black-
body radiation.[8] The energy of an individual photon is quantized and is greater
for photons of higher frequency. This relationship is given by Planck's
equation E = hf, where E is the energy per photon, f is the frequency of the
photon, and h is Planck's constant. A single gamma ray photon, for example,
might carry ~100,000 times the energy of a single photon of visible light.
The effects of EMR upon chemical compounds and biological organisms depend
both upon the radiation's power and its frequency. EMR of visible or lower
frequencies (i.e., visible light, infrared, microwaves, and radio waves) is
called non-ionizing radiation, because its photons do not individually have enough
energy to ionize atoms or molecules or break chemical bonds. The effects of these
radiations on chemical systems and living tissue are caused primarily by heating
effects from the combined energy transfer of many photons. In contrast, high
frequency ultraviolet, X-rays and gamma rays are called ionizing radiation, since
individual photons of such high frequency have enough energy
to ionize molecules or break chemical bonds. These radiations have the ability to
cause chemical reactions and damage living cells beyond that resulting from
simple heating, and can be a health hazard.
DISPLACEMENT CURRENT
Current in capacitors
Consider the charging capacitor in the figure.
All right copy reserved. No part of the material can be produced without prior permission

3. We have drawn two loops name as L which is outside the loop and Loop R which
is in between the parallel plates of capacitor.
The capacitor is in a circuit that transfers charge (on a wire external to the
capacitor) from the left plate to the right plate, charging the capacitor and
increasing the electric field between its plates. The same current enters the right
plate (say I ) as leaves the left plate. Although current is flowing through the
capacitor, no actual charge is transported through the vacuum between its plates
.
Ampere’s circuital is not applicable for loop L and we can find magnetic field at
point P using Ampere’s circuital law ∮𝐵⃗ ∙𝑑𝑙⃗⃗⃗ =𝜇0𝐼
Now if we consider an imaginary cylindrical surface. No conduction current enters
cylinder surface R, while current I leaves through surface L. Thus Ampere’s law is
not applicable and magnetic field at point P must be zero. So we have a
contradiction; calculated one way, there is a magnetic field at a point P; calculated
another way, the magnetic field at P is zero.
Nonetheless, a magnetic field exists between the plates as though a current were
present there as well.
For consistency of Ampere's Circuital law requires a displacement current ID = I to
flow across surface R.
The explanation is that a displacement current ID flows in the vacuum, and this
current produces the magnetic field in the region between the plates according to
Ampere’s law
If Q is the charge on capacitor plate and area of plates of capacitor is A
Electric field between plates
All right copy reserved. No part of the material can be produced without prior permission

4. 𝐸 = 𝑄 𝜀0𝐴
When capacitor is getting charged rate of change in electric field is
𝜕𝐸/ 𝜕𝑡 = 1 𝜀0𝐴 𝑑𝑄 /𝑑𝑡
= 𝜀0𝐴 𝜕𝐸/ 𝜕𝑡 = 𝐼𝐷
Here ID is called displacement current
In integral form 𝜀O ∫ 𝜕𝐸/𝜕𝑡 𝑑𝑎 = 𝐼𝐷
𝜀0 ∫ 𝑑𝜙𝐸/ 𝑑𝑡 = , where 𝑑𝜙𝐸/ 𝑑𝑡 is the rate of change of
electric flux
This current does not have significance in the sense of being the motion of
charges.
The generalization made by Maxwell then is the following. The source of a
magnetic field is not just the conduction electric current due to flowing charges,
but also the time rate of change of electric field. More precisely, the total current
I is the sum of the conduction current denoted by IC and the displacement current
denoted by ID
Adding integral form of displacement current in Ampere’s law we get
∮𝐵⃗ ∙ 𝑑𝑙⃗⃗⃗ = 𝜇0𝐼𝐶 +𝜇0𝜀0 ∫𝑑𝜙𝐸/ 𝑑𝑡
and is known as Ampere-Maxwell law.
Electromagnetic waves
According to Maxwell, an accelerated charge is a source of electromagnetic
radiation.
In an electromagnetic wave, electric and magnetic field vectors are at right angles
to each other and both are at right angles to the direction of propagation.
They possess the wave character and propagate through free space without any
material medium.
All right copy reserved. No part of the material can be produced without prior permission

5. These waves are transverse in nature. Fig shows the variation of electric field
E along Y direction and magnetic field B along Z direction and wave propagation
in + X direction
According to Maxwell’s theory, these electric and magnetic field do not come into
existence instantaneously.
In the region closer to the oscillating change, the phase
All right copy reserved. No part of the material can be produced without prior permission

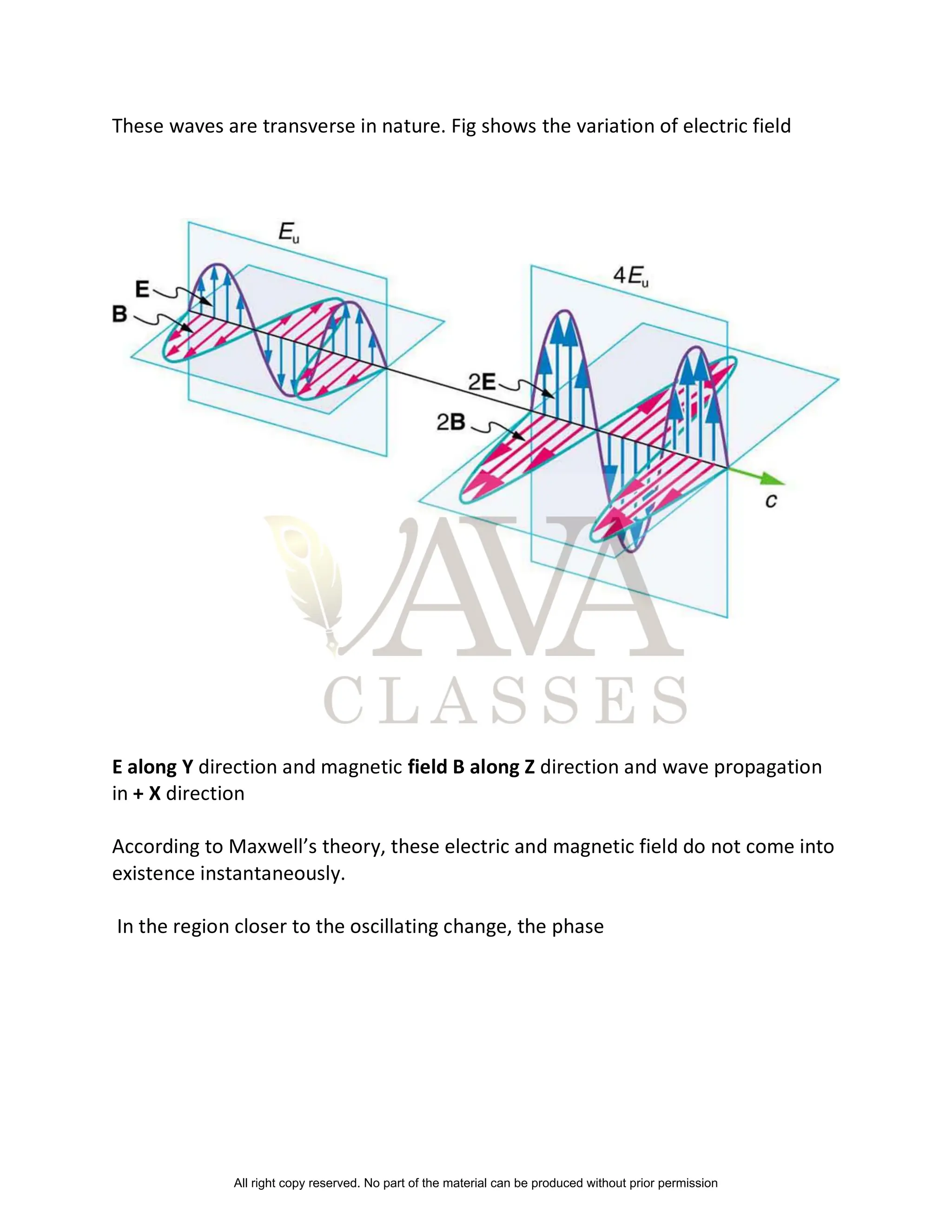
6. difference between electric field E and Magnetic field B is π/2 and their
magnitude quickly decreases as 1/r3 ( where r = distance from source) these
components are called Inductive component.
At larger distance E and B are in phase and the decrease in their magnitude is
comparatively slower with distance, as per 1/r. These components are called
radiated components
Characteristics of Electromagnetic waves
(1) Representation in form of equations:
Electromagnetic wave shown in figure at time t, the y component is
EY of electric field given by equation EY = E0 sin(ωt – kx)
In vector form E = EYj = [E0 sin(ωt – kx) ] j
Similarly Magnetic component is given as Bz =[B0 (ωt – kx) ] k
(2) Relation between magnitude of E and B is E = B/c
Here c is velocity of light
(3) The velocity of electromagnetic waves in vacuum
𝑐=1/√𝜀0𝜇0
The velocity of electromagnetic waves in medium
𝑣=1√𝜀𝜇
Here ε = permittivity of the medium and μ = permeability of the medium
(4) Electromagnetic waves are transverse in nature
(5) Electromagnetic waves posses energy and they carry energy from one place to
the other .
(6) Electromagnetic waves exerts pressure on a surface when they are incident on
it, called radiation pressure
All right copy reserved. No part of the material can be produced without prior permission

7. If ΔU is the energy of electromagnetic waves incident on a surface of area A in
time Δt , in direction normal to the surface and if all energy is absorbed then
change in momentum Δ𝑝 = Δ𝑈𝑐
(7) Energy density of electromagnetic wave
𝜌=𝜀0𝐸2
𝑟𝑚𝑠 and 𝜌=𝐵⃗2
𝑟𝑚𝑠/ 𝜇0
(8)The intensity of radiation (I) is defined as the radiant energy passing through
unit area normal to the direction of propagation in one second
𝐼=𝐸𝑛𝑒𝑟𝑔𝑦(𝑡𝑖𝑚𝑒)(𝑎𝑟𝑒𝑎)=𝑃𝑜𝑤𝑒𝑟
If radiation is passing through unit area with velocity c then volume in one second
= c
Thus energy volume = ρc from the value of ρ 𝑤𝑒 𝑔𝑒𝑡 𝐼=𝜀0𝑐𝐸𝑟𝑚𝑠2
Similarly 𝐼=𝑐𝐵⃗𝑟𝑚𝑠2/𝜇0
(9) E ×B gives the direction of propagation of the electromagnetic wave
E. M SPECTRUM
The sequential arrangement of all e. m waves
ELECTROMA
GNETIC
SPECTRUM
Sr. No.
Name Source Wavelength
in (m)
Frequency
range (Hz)
1 γ – rays Radioactive
nuclei,
nuclear
reactions
10−14 to
10−10
3 × 1022 to
3x 1018
2 x − rays High energy
electrons
suddenly
1 × 10−10 to
3 × 10−8
3 × 1018 to 1
× 1016
All right copy reserved. No part of the material can be produced without prior permission

8. stopped by a
metal target
3 Ultra−violet Atoms and
molecules in
electrical
discharge
6 x 10−10 to
4 × 10−7
5 x 1017 to 8
× 1014
4 Visible light incandescent
solids,
Fluorescent,
lamps
4 x 10−7 to
8 x 10−7
8 x 1014 to 4
x 1014
5 Infra−red (IR) molecules of
hot bodies
8 x 10−7 to
3x 10−5
4 x 1014 to 1
× 1013
6 Microwaves Electronic
device
(Vacuum
tube)
10−3 to
0.3
3 x 1011 to 1
x 109
7 Radio
frequency
wave
Charges
accelerated
through
conducting
wires
10 to
104
3 x 107 – 3 x
104
All right copy reserved. No part of the material can be produced without prior permission

9. All right copy reserved. No part of the material can be produced without prior permission

10. All right copy reserved. No part of the material can be produced without prior permission

11. All right copy reserved. No part of the material can be produced without prior permission

12. Radio waves:
These are the results of charges accelerating through conducting wires. They are
generated by such electronic devices as LC oscillators and are used in radio and
television communication systems.
Microwaves
have wavelengths ranging between approximately 1mm and 30 cm and are also
generated by electronic devices. Because of their short wavelength, they are well
suited for the radar systems used in aircraft navigation and for studying the atomic
and molecular properties of matter. Microwave ovens represent an interesting
domestic application of these waves.
Infrared waves
(sometimes called heat waves ) have wavelengths ranging from approximately
1mm to the longest wavelength of visible light, 7x 10-7
m. These waves produced
by the hot bodies and molecules, are readily absorbed by most materials. Infrared
radiation has many practical and scientific applications, including physical therapy,
infrared photography, and vibrational spectroscopy.
Visible light ,
The most familiar form of electromagnetic waves, is that part of the
electromagnetic spectrum that the human eye can detect. Light is produced by the
rearrangement of electrons in atoms and molecules .The various wavelengths of
visible light are classified with colors ranging from violet ( 4x 10 –7
m) to red ( 7X 10
–7 m.). The eye’s sensitivity is a function of wavelength, the sensitivity being a
maximum at a wavelength of about 5.6 X 10 –7
m (yellow-green).
Ultraviolet light
covers wavelengths ranging from approximately 3.8 X 10 –7
m(380 nm ) down to
6X10 –8 m (60nm).The Sun is a important source of ultraviolet light .Most of the
ultraviolet light from sun is absorbed by the atoms in the upper atmosphere, or
stratosphere. This is fortunate since UV light in large quantities produces harmful
effects on humans .One important constituent of the stratosphere is ozone (O3) ,
which results from reactions of ultraviolet radiation with oxygen.
X- Rays
All right copy reserved. No part of the material can be produced without prior permission

13. are electromagnetic waves with wavelengths in the range of approximately 10 –8
m (10nm) down to 10 –13m (19 –4 nm).The most common source of x-rays is the
deceleration of high energy electrons bombarding a metal target. X-rays are used
as a diagnostic tool in medicine and as a tool in medicine and as a treatment for
certain forms of cancer.
Gamma rays
are electromagnetic waves emitted by radioactive nuclei (such as 60
Co and 137
Cs)
and during certain nuclear reactions. They have wavelength ranging from
approximately 10-10 m to less than 10 –14 m. they are highly penetrating and
produce serious damage when absorbed by living tissues.
Uses of electromagnetic spectrum
The following are some of the uses of electromagnetic waves.
1. Radio waves : These waves are used in radio and television communication
systems. AM band is from 530 kHz to 1710 kHz.
Higher frequencies upto 54 MHz are used for short waves bands.
Television waves range from 54 MHz to 890 MHz.
FM band is from 88 MHz to 108 MHz.
Cellular phones use radio waves in ultra high
frequency (UHF) band.
2. Microwaves : Due to their short wavelengths, they are used in radar
communication system.
Microwave ovens are an interesting domestic application of these waves.
3. Infra red waves :
(i) Infrared lamps are used in physiotherapy.
(ii) Infrared photographs are used in weather forecasting.
(iii) As infrared radiations are not absorbed by air, thick fog, mist etc, they are
used to take photograph of long distance objects.
(iv) Infra red absorption spectrum is used to study the molecular structure.
4. Visible light : Visible light emitted or reflected from objects around us provides
information about the world. The wavelength range of visible light is 4000 Å to
8000 Å.
All right copy reserved. No part of the material can be produced without prior permission

14. 5. Ultra−violet radiations
(i) They are used to destroy the bacteria and for sterilizing surgical instruments.
(ii) These radiations are used in detection of forged documents, fingerprints in
forensic laboratories.
(iii) They are used to preserve the food items.
(iv) They help to find the structure of atoms.
6. X rays :
(i) X rays are used as a diagnostic tool in medicine.
(ii) It is used to study the crystal structure in solids.
7. γ−rays : Study of γ rays gives useful information about the nuclear structure
and it is used for treatment of cancer
All right copy reserved. No part of the material can be produced without prior permission

15. Solved Numerical
Q1) A 1000 W bulb is kept at the centre of a spherical surface and is at a distance
of 10 m from the surface. Calculate the force acting on the surface of the sphere
by the electromagnetic waves, along with E0, B0 and intensity I. Take the working
efficiency of the bulb to be 2.5% and consider it as a point source, , calculate the
energy density on the surface .
Solution:
The energy consumed every second by a 1000W bulb = 1000J
As the working efficiency of the bulb is equal to 2.5%, the energy radiated by the
bulb per second Δ𝑈=1000×2.5/100
∴Δ𝑈=25 𝐽𝑠−1
Considering, the bulb at the centre of the sphere, surface area of the sphere
A = 4πR2
= (4)(3.14)(102
) = 1256 m2
Intensity I 𝐼=𝐸𝑛𝑒𝑟𝑔/(𝑡𝑖𝑚𝑒)(𝑎𝑟𝑒𝑎)=25/1256=0.02𝑊𝑚−2
𝐼 = 𝜀0𝑐𝐸𝑟𝑚𝑠2=0.02
∴𝐸𝑟𝑚𝑠=⟦0.02/8.85×10−12
×3.0×105⟧1/2⁄=2.74 𝑉𝑚−1
NOW 𝐵⃗𝑟𝑚𝑠=𝐸𝑟𝑚𝑠 /𝑐 𝐵⃗𝑟𝑚𝑠=2.743/3.0×108
=9.13×10−9
𝑇
𝐸0=√2𝐸𝑟𝑚𝑠 𝐸0=1.41×2.74 =3.86 𝑉𝑚−1
𝐵⃗0=√2𝐵⃗ 𝐵⃗0=1.41×9.13×10−9=1.29×10−8 𝑇
The total energy incident on the surface = 25J
∴ The momentum (Δp) imparted to the surface in one second ( = force)
Δ𝑝=Δ𝑈𝑐=𝐹=253×108=8.33×10−8
𝑁
From I = ρc, energy density 𝜌=𝐼𝑐=0.023×108=6.67×10−11
𝐽𝑚−3
Q2) The maximum electric field at a distance of 10 m from an isotropic point
source of light is 3.0 V/m. Calculate (a) the maximum value of magnetic field (b)
average intensity of the light at that place and (c) the power of the source
εo = 8.854 × 10-12
C2
N-2
m-2
Solution
All right copy reserved. No part of the material can be produced without prior permission

16. (a)maximum value of magnetic field
E = Bc 𝐵⃗=𝐸𝑐=3./03.0×108=10−8T
(b) average intensity of the light at that place
From formula 𝐼=𝜀0𝑐𝐸𝑟𝑚𝑠
2
=𝜀0𝑐×𝐸022 𝐼=8.854×10−12
×3.0×108
×(3.0)2 /
2
𝐼=1.195×10−2 𝑤𝑚−2
(c) Power
Power = I × Area = I ×4πr2
Power = 1.195×10-2×4×3.14×(10)2 = 15 w
----------------END--------------
All right copy reserved. No part of the material can be produced without prior permission

17. All right copy reserved. No part of the material can be produced without prior permission