The document discusses the concept of equilibrium in physical and chemical contexts, defining stable and unstable equilibrium and explaining dynamic equilibrium in reversible chemical reactions. It also covers the characteristics of chemical equilibrium, the law of mass action, and the relationships between equilibrium constants for various types of reactions, including how changes in conditions affect equilibrium states. It highlights the importance of understanding reactants and products, as well as the distinctions between homogeneous and heterogeneous equilibria.
![[Type here]
All right copy reserved. No part of the material can be produced without prior permission
Key Features
All-in one Study Material (for Boards/IIT/Medical/Olympiads)
Multiple Choice Solved Questions for Boards & Entrance Examinations
Concise, conceptual & trick – based theory
Magic trick cards for quick revision & understanding
NCERT & Advanced Level Solved Examples](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-1-2048.jpg)


![All right copy reserved. No part of the material can be produced without prior permission
80% of the mixture would be converted to HI. If HI is heated at 440C, only 20% would be
converted into H2 and I2. This is an unfailing criterion of a chemical equilibrium.
If one of the conditions (temperature, pressure or concentration) under which an equilibrium
exists is altered, the equilibrium shifts and a new state of equilibrium is reached.
A catalyst does not alter the position of equilibrium. It accelerates both the forward and
reverse reactions to the same extent and so the same state of equilibrium is reached but
quickly. So a catalyst hastens the attainment of equilibrium.
If the reactants and the products in a system are in the same phase, the equilibrium is said to be
homogeneous.
For example,
H2(g) + I2(g) 2HI(g)
represents a homogeneous equilibrium in gaseous phase and
CH3CO2H(l) + C2H5OH(l) CH3CO2C2H5(l) + H2O(l)
represents a homogeneous equilibrium in solution phase.
A phase is a homogeneous (same composition and properties throughout) part of a system,
separated from other phases (or homogeneous parts) by bounding surfaces.
Any number of gases constitute only one phase.
In liquid systems, the number of phases = number of layers in the system. Completely miscible
liquids such as ethanol and water constitute a single phase. On the other hand, benzene - water
system has 2 layers and so two phases.
Each solid constitutes a separate phase, except in the case of solid solutions. [A solid solution, e.g.,
lead and silver, forms a homogeneous mixture.]
If more than one phase is present in a chemical equilibrium, it is said to be heterogeneous
equilibrium.
For example,
CaCO3(s) CaO(s) + CO2(g)
represents a heterogeneous equilibrium involving two solid phases and a gaseous phase.
The law of mass action (given by Guldberg and Waage) states that the rate of a chemical
reaction is proportional to the product of effective concentrations (active masses) of the reacting species,
each raised to a power that is equal to the corresponding stoichiometric number of the substance
appearing in the chemical reaction.
By the rate of a chemical reaction we mean the amount of reactant transformed into products in
unit time. It is represented by dx/dt.
Active mass means the molar concentration, i.e., the number of moles in
1 litre. Suppose 3 moles of nitrogen are present in a 4 litre vessel, the active mass of nitrogen
= 3/4 = 0.75 mole/litre. Active mass of a substance is represented by writing molar concentration in square
brackets.
Active mass of reactant molarity
Active mass of reactant = molarity
where is the activity coefficient.
a = molarity
THE LAW OF MASS ACTION
3](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-4-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
For very dilute solutions, the value of activity coefficient is unity.
activity(a) = molarity.
Thus, in place of activity of any reactive species, molarity can be used for dilute solutions.
In IITJEE Syllabus, only dilute solutions are there, so everywhere we would be using the term molarity in
place of active mass of a species.
(i) Let us have an equilibrium reaction as
X(g) + Y(g) Z(g)
For this reaction, which is in equilibrium, there exist an equilibrium constant (Keq)
represented as
]
Y
[
]
X
[
]
Z
[
K eq
For the given equilibrium, irrespective of the reacting species (i.e, either X + Y or Z or X +
Z or Y + Z or X + Y + Z) and their amount we start with, the ratio,
]
Y
[
]
X
[
]
Z
[
is always
constant at a given temperature. This really looks amazing. Isn’t it? Let us see, how such
a thing is possible.
We have learnt that at the equilibrium, rate of forward and reverse reactions are equal
and we also know the law of mass action. Using this, we can write
Rate of forward reaction [X] [Y]
Rate of forward reaction = kf [X] [Y]
where kf is the rate constant for the forward reaction.
Similarly, rate of reverse reaction [Z]
Rate of reverse reaction = kr [Z]
where kr is the rate constant for the reverse reaction.
At equilibrium,
Rate of forward reaction = Rate of reverse reaction.
kf [X] [Y] = kr [Z]
]
Y
[
]
X
[
]
Z
[
k
k
r
f
Since, kf and kr are constants at a given temperature, so their ratio
r
f
k
k
would also be a
constant, referred as Keq.
]
Y
[
]
X
[
]
Z
[
Keq
As Keq is the ratio of rate constants for forward and reverse reaction, so the value of Keq
would always be a constant and will not depend on the species we have started with and
their initial concentrations.
The given expression involves all variable terms (variable term means the concentration
of the involved species changes from the start of the reaction to the stage when
equilibrium is reached), so the ratio
]
Y
[
]
X
[
]
Z
[
can also be referred as KC.
EQUILIBRIUM CONSTANT, 𝑲𝒆𝒒 , 𝑲𝑪 , 𝑲𝑷 𝑨𝑵𝑫 𝑲𝑷𝑪
4](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-5-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
]
Y
[
]
X
[
]
Z
[
KC
Thus, for the given equilibrium, it seems that Keq and KC are same but in actual practice
for some other equilibrium, they are not same.
Assuming that the gases X, Y and Z behave ideally, we can use ideal gas equation for
them.
PV = nRT
cRT
RT
V
n
P
RT
P
c
RT
P
]
Z
[
and
RT
P
]
Y
[
;
RT
P
]
X
[ Z
y
x
RT
P
RT
P
RT
P
K
Y
X
Z
C =
Y
X
Z
P
P
RT
P
Y
X
Z
C
P
P
P
RT
K
The LHS of the above expression is a constant since KC , R and T, all are constant.
This implies that RHS is also a constant, which is represented by KP.
Y
X
Z
P
P
P
P
K
Thus, expression of KP involves partial pressures of all the involved species and
represents the ratio of partial pressures of products to reactants of an equilibrium
reaction.
(ii) Now, let us change the phase of reactant X from gaseous to pure solid. Then the
equilibrium reaction can be shown as
X(s) + Y(g) Z(g)
Its equilibrium constant (Keq) would be
]
Y
[
]
X
[
]
Z
[
Keq
Concentration of Y and Z is their respective number of moles per unit volume of the
container (as the volume occupied by the gas is equal to the volume of the container).
The concentration of X is the number of moles of X per unit volume of solid. As we know,
the concentration of all pure solids (and pure liquids) is a constant as it is represented by
d/M (where d and M represents its density and molar mass). This ratio of d/M will be a
constant whether X is present initially or at equilibrium. This means that the concentration of X
is not varying, but is a constant, which can be merged with Keq to give another constant, called
KC.
]
Y
[
]
Z
[
]
X
[
Keq ](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-6-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
]
Y
[
]
Z
[
KC
Thus expression of KC involves only those species whose concentration changes during
the reaction.
The distinction between Keq and KC is that the expression of Keq involves all the
species (whether they are pure solids, pure liquids, gases, solvents or solutions)
while the KC expression involves only those species whose concentration is a
variable (like gases and solutions). Thus, expression of KC is devoid of pure
components (like pure solids and pure liquids) and solvents.
Y
Z
Y
Z
C
P
P
RT
P
RT
P
K
Since, LHS of the expression is a constant, so the ratio
Y
Z
P
P
would also be a constant,
represented by KP.
Y
Z
P
P
P
K
(iii)Now, let us change the phase of reactant X from pure solid to solution and add another
gaseous product. The equilibrium reaction can now be represented as
X(soln.) + Y(g) Z(g) + A(g)
]
Y
[
]
X
[
]
A
[
]
Z
[
Keq
We have seen above that concentration of Y, Z and A is a variable but what about the
concentration of X now. Let us see. X in solution phase means some moles of X (solute)
are dissolved in a particular solvent. The concentration of X is thus given as the number
of moles of X per unit volume of solution(volume of the solution has major contribution
from the volume of solvent and the volume of solute hardly contributes to it). Let the
number of moles of X taken initially are ‘a’, which are dissolved in ‘V’ litre of solvent. So,
the initial concentration of X is
V
a
. Now at equilibrium, the moles of X reacted with Y be
‘x’. Thus the concentration of X now becomes
V
a x
. This shows that the concentration
of X changes during the reaction and X is thus a variable.
Thus, given expression of Keq involve all variable terms, so the ratio
]
Y
[
]
X
[
]
A
[
]
Z
[
can also be
referred as KC.
]
Y
[
]
X
[
]
A
[
]
Z
[
KC
Now, if we try to express the concentration of X, Y, Z and A in terms of partial pressures,
we would be able to do it only for Y, Z and A but not for X, since it is a solution. As the
concentration of X cannot be expressed in terms of its pressure or vapour pressure and](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-7-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
constants, so it should be kept as concentration term only in the equilibrium constant
expression.
RT
P
]
X
[
P
P
RT
P
]
X
[
RT
P
RT
P
K
Y
A
Z
Y
A
Z
C
Y
A
Z
C
P
]
X
[
P
P
)
RT
(
K
The LHS of the expression is a constant (as KC, R and T all are constant), which implies
that the RHS will also be a constant. But RHS of the expression can neither be called KP
(as all are not partial pressure terms) nor KC (as all are not concentration terms), so such
expression that involves partial pressure and concentration terms both are referred as
KPC.
Y
A
Z
C
P
P
]
X
[
P
P
K
Thus, KP can exist only for that equilibrium which satisfies these two conditions.
(a) At least one of the reactant or product should be in gaseous phase and
(b) No component of the equilibrium should be in solution phase (because when
solution is present, the equilibrium constant would be called KPC).
(iv)Let us consider a different equilibrium reaction of the type,
n1A(g) + n2B(g) m1C(g) + m2D(g)
The equilibrium constant, Keq would be
2
1
2
1
n
n
m
m
eq
]
B
[
]
A
[
]
D
[
]
C
[
K
Since, in this expression all the terms involved are variables, so the ratio
2
1
2
1
n
n
m
m
]
B
[
]
A
[
]
D
[
]
C
[
would also be a constant called Kc.
2
1
2
1
n
n
m
m
C
]
B
[
]
A
[
]
D
[
]
C
[
K
The concentration terms can be replaced by
RT
P
for each gaseous species.
Thus,
2
n
B
1
n
A
2
m
D
1
m
C
C
RT
P
RT
P
RT
P
RT
P
K
Rearranging the expression gives
2
1
2
1
2
1
2
1
n
B
n
A
m
D
m
C
)
n
n
(
)
m
m
(
C
)
P
(
)
P
(
)
P
(
)
P
(
)
RT
(
K
…..(i)
The LHS of the expression is a constant since KC, R, T and all stoichiometric coefficients
are constant. So, RHS of the expression would also be a constant called as KP (as the
RHS involved all partial pressure terms).](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-8-2048.jpg)

![All right copy reserved. No part of the material can be produced without prior permission
The reaction quotient is defined as the ratio of concentration of the reacting species at any point
of time other than the equilibrium stage. It is represented by Q. Thus, inserting the starting concentrations
of H2, I2 and HI in the equilibrium constant expression gives
)
146
.
0
(
)
243
.
0
(
)
98
.
1
(
]
[
]
H
[
]
H
[
Q
2
0
2
0
2
2
0
I
I
= 110.5
where the subscript 0 indicates initial concentrations (before equilibrium is reached).
As we know that every reaction has a tendency to attain equilibrium, so Q value should approach
Kc value. In the present case, Q value is greater than Kc value, so value of Q can approach Kc value only
when HI starts converting into H2 and I2. Thus, when Q > Kc, the net reaction proceeds from right to left to
reach equilibrium.
To determine the direction in which the net reaction will proceed to achieve equilibrium, we
compare the values of Q and Kc. The three possible cases are as follows:
(a) Q > Kc: For such a system, products must be converted to reactants to reach equilibrium. The
system proceeds from right to left (consuming products, forming reactants) to reach equilibrium.
(b) Q = Kc: The initial concentrations are the equilibrium concentrations. So, the system is already
at equilibrium.
(c) Qc < Kc: For such a system, reactants must be converted to products to reach equilibrium. The
system proceeds from left to right (consuming reactants, forming products) to attain equilibrium.
7.1 NATURE OF REACTANTS AND/OR PRODUCTS
The value of equilibrium constant depends on the nature of reactants as well as on the products. By
changing reactant(s) or product(s) of a reaction, the equilibrium constant of the reaction changes.
For example,
N2(g) + O2(g) 2NO(g) ;
]
O
[
]
N
[
]
NO
[
K
2
2
2
1
C
N2(g) + 2O2 2NO2(g) ; 2
2
2
2
2
2
C
]
O
[
]
N
[
]
NO
[
K
Although the reactants are same in the two reactions but the products being different, the value of
equilibrium constant for the two reactions will be different. If we start with ‘a’ and ‘b’ moles of N2 and O2
respectively in both the reactions, carried out in same vessel (V litre capacity), the extent of two reactions
occurring will be different and thus, the KC for the two reactions differ.
Similarly for reactions,
H2(g) + I2(g) 2HI(g)
H2(g) + Cl2(g) 2HCl(g)
The values of the equilibrium constant for the two reactions will be completely different as one of
the reactant in the two reactions is different.
7.2 TEMPERATURE
The variation of equilibrium constant with temperature is given by the relation
log .
T
1
T
1
R
303
.
2
H
K
K
2
1
1
2
This can be obtained by the help of Arrhenius equation.
The Arrhenius equation for the rate constant of forward reaction is
kf =
RT
/
)
f
(
a
E
f e
A
………(2)
FACTORS AFFECTING EQUILIBRIUM CONSTANT
7](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-10-2048.jpg)

![All right copy reserved. No part of the material can be produced without prior permission
(a) When H is positive (endothermic reactions), an increase in temperature (T2 > T1) will make
2
T
K > 1
T
K , i.e. the reaction goes more in the forward direction and with decrease in
temperature, reaction goes in reverse direction.
(b) When H is negative (exothermic reactions), an increase in temperature (T2 > T1), will take
2
T
K < 1
T
K i.e., the reaction goes in the reverse direction and with decrease in temperature,
reaction goes in the forward direction.
(c) The calculation of equilibrium constant from kinetic consideration is only one of the many
approaches. Since equilibrium constant is a thermodynamic quantity its definition and
calculation involve detailed thermodynamical consideration which is beyond the scope of IIT
JEE syllabus.
7.3 STOICHIOMETRY OF THE EQUILIBRIUM REACTION
The value of KP and KC depends upon the stoichiometry of reaction since the law of mass reaction
makes use of the given stoichiometric coefficients of the reaction.
N2(g) + 3H2(g) 2NH3(g)
KC =
3
2
2
2
3
H
N
NH
………(i)
)
g
(
H
2
3
)
g
(
N
2
1
2
2 NH3(g)
C
K = 2
/
3
2
2
/
1
2
3
]
H
[
]
N
[
]
NH
[
………(ii)
From equation (i) and (ii)
C
C K
K
Thus, in general if an equilibrium reaction is multiplied by ‘n’, the equilibrium constant of the new
reaction would become nth
power of the equilibrium constant of old reaction.
(KC)new = n
old
C )
K
(
7.4 MODE OF WRITING A CHEMICAL EQUATION
The value of KP and KC also depend on the method of representing a chemical equation.
For example,
N2(g) + 3H2(g) 2NH3(g)
KC =
3
2
2
2
3
H
N
NH
When the equilibrium reaction is reversed,
2NH3(g) N2(g) + 3H2(g)
C
K
=
C
2
3
3
2
2
K
1
]
NH
[
]
H
[
]
N
[
Now, if we write the equilibrium reaction as,
NH3(g) ½N2(g) + 3/2 H2(g)
C
K
=
C
3
2
/
3
2
2
/
1
2
K
1
]
NH
[
]
H
[
]
N
[
DEGREE OF DISSOCIATION
8](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-12-2048.jpg)

![All right copy reserved. No part of the material can be produced without prior permission
at equil.
V
a x
V
b x
V
2x
KC =
x
x
x
x
x
x
2
b
a
4
V
b
V
a
V
2
]
[
]
H
[
]
H
[
2
2
2
2
I
I
Let PT be the total pressure at the equilibrium.
T
T
2
T
2
2
H
2
H
P
P
b
a
b
P
b
a
a
P
b
a
2
)
P
(
)
P
(
)
P
(
K
x
x
x
I
I
=
x
x
x
b
a
4 2
Thus, Kp = Kc
Also from the relation, Kp = Kc(RT)n
Since, n for this equilibrium reaction is zero,
Kp = Kc
Illustration 1
Question: In an experiment it was found that when 20.55 moles of hydrogen were heated with
31.89 moles of iodine at 440C, the equilibrium mixture contained 2.06 moles of
hydrogen, 13.40 moles of iodine and 36.98 moles of HI. Calculate the equilibrium
constant for the reaction H2(g) + I2(g) 2HI(g).
Solution: In the problem, initial moles of H2 and I2 are given. The moles of H2, I2 and HI are also given
at equilibrium, so the initial moles are not needed in the problem to calculate Kc. Let the
volume of the container be ‘V’ litre.
KC =
40
.
13
06
.
2
98
.
36
V
40
.
13
V
06
.
2
V
98
.
36
]
[
]
H
[
]
H
[ 2
2
2
2
2
I
I
= 49.54
Illustration 2
Question: A sample of HI was found to be 22% dissociated when equilibrium was reached. What
will be the degree of dissociation if hydrogen is added in the proportion of 1 mole for
every mole of HI originally present, the temperature and volume of the system being
kept constant?
Solution: The degree of dissociation () is the fraction of 1 mole of HI that has dissociated under the
given conditions. If the % dissociation of HI is 22, the degree of dissociation is
100
22
= 0.22.
2HI(g) H2(g) + I2(g)
Moles at equil. 1 /2 /2
1 0.22 = 0.78 0.11 0.11
KC =
2
2
2
78
.
0
11
.
0
11
.
0
]
H
[
]
[
]
H
[
I
I2
= 0.0199](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-14-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
Let us now add 1 mole of hydrogen when we start with 1 mole of HI. Let x be the
degree of dissociation.
2HI(g) H2(g) + I2(g)
Moles at equil. 1 x
1
2
x
2
x
KC =
2
2
2
1
2
1
2
]
H
[
]
[
]
H
[
x
x
x
I
I2
= 0.0199
x = 0.037 or –2.4 (not admissible)
Degree of dissociation = 0.037
% of dissociation = 3.7
(Introduction of H2 suppresses the dissociation of HI)
(ii) Thermal dissociation of PCl5
When PCl5 is heated in a closed vessel at a steady temperature (above 200C), the
following equilibrium is established.
PCl5(g) PCl3(g) + Cl2(g)
Moles at equil. 1
Let be the degree of dissociation. Then at equilibrium we will have (1 – ) mole of PCl5,
mole of PCl3 and mole of Cl2. If ‘V’ litres is the capacity of the vessel, then molar
concentration of various species would be
[PCl5] =
1
V
; [PCl3] =
V
; [Cl2] =
V
KC =
V
1
V
V
]
PCl
[
]
Cl
[
]
PCl
[
5
2
3
=
2
1
V( )
Let PT be the total pressure of the equilibrium system.
KP =
T
T
T
5
PCl
2
Cl
3
PCl
P
1
1
P
1
P
1
P
P
P
= 2
T
2
1
P
KP KC (since n is not zero)
Illustration 3
Question: 0.1 mole of PCl5 is vapourized in a litre vessel at 200C. What will be the concentration
of chlorine at equilibrium if the equilibrium constant KC for the dissociation of PCl5 at
this temperature is 0.0414?
Solution: PCl5(g) PCl3(g) + Cl2(g)
Moles at equil. 1 x x x
Let x moles of chlorine be present at equilibrium
[PCl5] =
1
1
.
0 x
= 0.1 – x ; [PCl3] = x ; [Cl2] = x
KC = 0.0414 =
]
PCl
[
]
Cl
[
]
PCl
[
5
2
3
=
x
x
1
.
0
2](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-15-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
x = 0.0469 moles/litre
[Cl2] = 0.0469 moles/litre
Illustration 4
Question: What will be the degree of dissociation of PCl5 when 0.1 mole of PCl5 is placed in a 3 L
vessel containing chlorine at 0.5 atm pressure and 250C? (KP = 1.78)
Solution: KP =
5
2
3
PCl
Cl
PCl
P
P
P
= 1.78
Let x be the amount of PCl5 dissociated at equililbrium.
V
RT
P 3
PCl
x
;
V
RT
P 2
Cl
x
+ 0.5 ;
V
RT
)
1
.
0
(
P 5
PCl
x
1.78 =
V
RT
)
1
.
0
(
5
.
0
V
RT
V
RT
x
x
x
=
x
x
x
1
.
0
5
.
0
3
523
082
.
0
x = 0.0574 mole
Degree of dissociation () of PCl5 is the fraction of 1 mole that has dissociated.
=
1
.
0
0574
.
0
= 0.574.
(iii) Thermal dissociation of dinitrogen tetroxide
Between 22C and 150C, N2O4 undergoes thermal dissociation and the gas mixture
consists of N2O4 and NO2 in reversible equilibrium.
N2O4(g) 2NO2(g) (endothermic)
If 1 mol of N2O4 is enclosed in a vessel of volume ‘V’ litre and at equilibrium, is the
degree of dissociation of N2O4, then
[N2O4] =
1
V
; [NO2] =
2
V
KC =
V
1
V
2
]
O
N
[
]
NO
[
2
4
2
2
2
4
1
2
V( )
T
2
T
4
O
2
N
2
2
NO
P
P
1
1
P
1
2
)
P
(
)
P
(
K = 2
T
2
1
P
4
where PT is the total equilibrium pressure.
KP KC (since n is not zero)
Illustration 5
Question: The equilibrium constant KP for the reaction N2O4(g) 2NO2(g) at 497C is found
to be 636 mm Hg. If the pressure of the gas mixture is 182 mm, calculate the percentage
dissociation of N2O4. At what pressure will it be half dissociated?
Solution: KP = 2
T
2
1
P
4
](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-16-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
636 = 2
2
1
182
4
636 – 6362
= 7282
13642
= 636
2
=
636
1364
= 0.4663 ; = 4663
.
0 = 0.6829
% dissociation of N2O4 = 0.6829 100 = 68.29
When the gas is half dissociated, = 0.5
Let the pressure be T
P mm Hg.
636 =
2
T
2
)
5
.
0
(
1
P
)
5
.
0
(
4
T
P = 477 mm
(iv) Synthesis of ammonia (Haber’s process)
N2(g) + 3H2(g) 2NH3(g) ; H = 46 kJ mol1
Suppose we start with 1 mole of nitrogen and 3 moles of H2 in a vessel of capacity ‘V’
litres and heat the mixture at a steady temperature (250C) under pressure.
Let x moles of N2 react. Then
N2(g) + 3H2(g) 2NH3(g)
Molar conc. at
V
1 x
V
)
1
(
3 x
V
2x
equilibrium
KC = 3
2
3
2
2
2
3
V
)
1
(
3
V
1
V
2
]
H
[
]
N
[
]
NH
[
x
x
x
= 4
2
2
)
1
(
27
V
4
x
x
KP =
3
2
H
2
N
2
3
NH
P
P
P
= 3
T
T
2
T
P
2
4
)
1
(
3
P
2
4
)
1
(
P
2
4
2
x
x
x
x
x
x
=
2
T
4
2
2
P
)
1
(
27
)
2
4
(
4
x
x
x
where PT is the total pressure at equilibrium.
KP KC (as n is nonzero)
Illustration 6
Question: For the reaction
N2(g) + 3H2(g) 2NH3(g) ; H = 46 kJ mol1
Calculate the value of KP. Given KC = 0.5 lit2
mol2
at 400C.
Solution: KP = KC(RT)n
n = 2 – 4 = 2](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-17-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
KP = 0.5(0.082 673)2
= 2
)
673
082
.
0
(
5
.
0
= 1.641 104
.
Illustration 7
Question: 1 mole of nitrogen is mixed with 3 moles of hydrogen in a 4 L container. If 0.25% of N2
is converted into ammonia by the following reaction
N2(g) + 3H2(g) 2NH3(g)
Calculate the equilibrium constant KC in concentration units. What will be the value of
KC for the following equilibrium?
1
2
N2(g) +
3
2
H2(g) NH3(g)
Solution: N2 + 3H2 2NH3
Initial 1 3 0 moles
Let x moles of N2 react at equilibrium.
Then 1 – x 3 – 3x 2x moles at equilibrium
KC =
3
2
V
3
3
V
1
V
2
x
x
x
=
4
2
2
)
1
(
27
V
4
x
x
=
4
2
2
)
0025
.
0
1
(
27
4
)
0025
.
0
(
4
KC = 1.496 105
litre2
mole2
KC =
3
2
2
2
3
]
H
[
]
N
[
]
NH
[
For the equilibrium 2
2 H
2
3
N
2
1
NH3, the equilibrium constant would be
2
/
3
2
2
/
1
2
3
c
]
H
[
]
N
[
]
NH
[
K
=
c
K 5
c 10
496
.
1
K
= 3.86 103
litre mol1
9.2 HOMOGENEOUS EQUILIBRIA IN SOLUTION PHASE
Formation of ethyl acetate
This equilibrium can be represented by the equation
C2H5OH(l) + CH3COOH(l) CH3COOC2H5(l) + H2O(l)
Although for each species, we write l in the parenthesis but they are not pure liquids. Once
the liquids are mixed, they form a homogeneous solution. Thus, the concentration of each species
changes during establishment of equilibrium. If the system behaved ideally,
]
COOH
CH
[
]
OH
H
C
[
]
O
H
[
]
H
COOC
CH
[
K
3
5
2
2
5
2
3
c
Let the total volume of the solution be ‘V’ litre and the initial number of moles of acetic
acid and that of ethanol be ‘a’ and ‘b’ respectively.
Let ‘x’ moles of acetic acid react at equilibrium. Then ‘x’ moles of ethyl acetate and ‘x’
moles of water would be formed. At equilibrium,
[CH3COOH] =
V
a x
; [C2H5OH] =
V
b x
; [CH3COOC2H5] =
V
x
; [H2O] =
V
x](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-18-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
KC =
)
b
(
)
a
(
V
)
b
(
V
)
a
(
V
V
2
x
x
x
x
x
x
x
Illustration 8
Question: Determine the amount of ester present under equilibrium when 3 moles of ethyl alcohol
react with 1 mole of acetic acid, when equilibrium constant of the reaction is 4.
Solution: CH3COOH + C2H5OH CH3COOC2H5 + H2O
1 – x 3 – x x x
KC = 4 =
)
3
(
)
1
( x
x
x
x
= 2
2
4
3 x
x
x
3x2
– 16x + 12 = 0
x = 0.903 or 4.43 (inadmissible)
Amount of ester at equilibrium = 0.903 mole.
9.3 EQUILIBRIUM CONSTANT FOR VARIOUS HETEROGENEOUS EQUILIBRIA
Heterogeneous equilibrium results from a reversible reaction involving reactants and products that
are in different phases. The law of mass action applicable to a homogeneous equilibrium is also
applicable to a heterogeneous system.
(a) Decomposition of solid CaCO3 into solid CaO and gaseous CO2
Let ‘a’ moles of CaCO3 are taken in a vessel of volume ‘V’ litre at temperature ‘T’ K.
CaCO3(s) CaO(s) + CO2(g)
Moles initially a 0 0
Moles at equilibrium a x x x
Keq =
]
CaCO
[
]
CO
[
]
CaO
[
3
2
As CaCO3 and CaO(s) are pure solids, so their d/M is a constant and their concentrations do not
change as long as they are present. Thus the equilibrium expression can be rearranged as
Keq ]
CO
[
]
CaO
[
]
CaCO
[
2
3
It can be seen that left hand side of the equation is a constant represented by Kc.
Kc = [CO2] =
V
x
……..(i)
Assuming CO2 gas to behave ideally at the temperature & pressure of the reaction, the molar
concentration of CO2 can be written using ideal gas equation as
RT
P 2
CO
.
Kc =
RT
P 2
CO
Kc(RT) = 2
CO
P
Since Kc, R and T are constants, their product will also be a constant referred as Kp.
Kp = 2
CO
P =
V
RT
x
……..(ii)
From equation (i) and (ii), it is clear that whenever the equilibrium would be attained at ‘T’
K, in a vessel of volume ‘V’ litre, the moles of CO2 present at equilibrium should be
x (which can exert a pressure equal to )
P 2
CO If rather than starting with ‘a’ mole of CaCO3, we](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-19-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
start with x moles of CaCO3 in the vessel of volume ‘V’ at ‘T’K, then the entire CaCO3 would
have decomposed to give CO2 but the equilibrium can not be maintained as there would be no
CaCO3 left. Further if the moles of CaCO3 taken in the same vessel at same temperature were less
than x, the equilibrium would never be attained. Thus, any amount (moles) of CaCO3 more than x
would be sufficient to establish the equilibrium. So the minimum moles of CaCO3 required would
be x, as any moles more than this would be sufficient to establish the equilibrium. So the minimum
moles of CaCO3 required to attain equilibrium under given conditions would be x.
The given equilibrium can be made to move in the forward direction by either removing
some moles of CO2 or by increasing the volume of the container or by increasing the temperature
of the reaction (as the reaction is endothermic). Addition of solid CaCO3 or CaO to the equilibrium
mixture will not affect the equilibrium at all.
For such equilibria, at any temperature, there will be a fixed value of the pressure of CO2,
which is called as dissociation pressure. The dissociation pressure of heterogeneous equilibria is
defined as the total pressure exerted by the gaseous species in equilibrium with the solid species.
The relation giving the variation of Kp with temperature is
log
2
1
1
T
p
2
T
p
T
1
T
1
R
303
.
2
H
)
K
(
)
K
(
Illustration 9
Question: Consider the following heterogeneous equilibrium,
CaCO3(s) CaO(s) + CO2(g).
At 800°C, the pressure of CO2 is 0.236 atm. Calculate
(a) Kp and (b) Kc for the equilibrium reaction at this temperature.
Solution: For the given equilibrium, partial pressure of CO2 is nothing but equal to Kp.
Kp = 2
CO
p = 0.236 atm
For an equilibrium reaction,
Kp = Kc(RT)n
As n = 1, so Kc =
1073
0821
.
0
236
.
0
RT
Kp
Kc = 2.68 103
moles/litre
(b) Reaction of solid phosphorous with gaseous Cl2 to form liquid PCl3
P4(s) + 6Cl2(g) 4PCl3(l)
The equilibrium constant is given by
6
2
4
4
3
eq
Cl
P
PCl
K
Since, pure solids and pure liquids do not appear in the equilibrium constant expression, thus
expression can be rearranged as
6
2
4
3
4
eq
Cl
1
PCl
P
K
Kc = 6
2 ]
Cl
[
1
Alternatively, we can express the equilibrium constant in terms of the pressure of Cl2.
Kp = 6
2
Cl )
p
(
1
(iii) Dissociation of ammonium hydrogen sulfide](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-20-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
Let the moles of NH4HS(s) taken in a vessel of volume ‘V’ litre be ‘a’ at temperature ‘T’K.
At equilibrium, x moles of NH4HS dissociates to give NH3(g) and H2S(g).
NH4HS(s) NH3(g) + H2S(g)
Moles initially a 0 0
Moles of equilibrium a x x x
Keq =
]
HS
NH
[
]
S
H
[
]
NH
[
4
2
3
As the concentration of NH4HS is a constant, so it can be merged with Keq to get KC.
Keq [NH4HS] = [NH3] [H2S]
KC = [NH3] [H2S] =
2
V
V
V
x
x
x
Assuming H2S and NH3 to behave ideally at the given temperature and pressure of the
reaction, the molar concentration of the gas can be written as .
RT
P
[NH3] = [H2S] =
RT
P
RT
P S
2
H
3
NH
KC =
RT
P
RT
P S
2
H
3
NH
KC(RT)2
= S
2
H
3
NH P
P
Since, LHS of the expression is a constant, it can be represented by another constant, KP.
KP = .
P
P S
H
NH 2
3
If the dissociation pressure measured for NH4HS be PT atm, then
S
H
NH 2
3
P
P =
2
PT
KP =
4
P
2
P
2
P
2
T
T
T
We have so far considered relatively simple equilibrium reactions. Let us take a slightly
complicated situation, in which the product molecules(s) in one equilibrium system are involved in a
second equilibrium process.
A(g) + B(g) C(g) + D(g) ;
]
B
[
]
A
[
]
D
[
]
C
[
K 1
C
C(g) + E(g) F(g) + G(g) ;
]
E
[
]
C
[
]
G
[
]
F
[
K 2
C
Overall reaction: A(g) + B(g) + E(g) D(g) + F(g) + G(g) ;
]
E
[
]
B
[
]
A
[
]
G
[
]
F
[
]
D
[
K 3
C
In this case, one of the product molecule, C(g) of the first equilibrium reaction combines with E(g)
to give F(g) and G(g) in another equilibrium reaction, so in the overall reaction, C(g) will not appear on
either side.
MULTIPLE EQUILIBRIA
10](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-21-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
The equilibrium constant )
K
( 3
C of the overall reaction can be obtained if we take the product of the
expressions of )
K
( 1
C and )
K
( 2
C .
]
E
[
]
B
[
]
A
[
]
G
[
]
F
[
]
D
[
]
E
[
]
C
[
]
G
[
]
F
[
]
B
[
]
A
[
]
D
[
]
C
[
K
K 2
C
1
C
3
C
2
C
1
C K
K
K
Thus, if a equilibrium reaction can be expressed as the sum of two or more equilibrium
reactions, then the equilibrium constant for the overall reaction is given by the product of the
equilibrium constants of the individual reactions.
When more than one equilibrium are established in a vessel at the same time and any one of the
reactant or product is common in more than one equilibrium, then the equilibrium concentration of the
common species in all the equilibrium would be same.
For example, if we take CaCO3(s) and C(s) together in a vessel of capacity ‘V’ litre and heat it at
temperature ‘T’ K, then CaCO3 decomposes to CaO(s) and CO2(g). Further, evolved CO2 combines with
the C(s) to give carbon monoxide. Let the moles of CaCO3 and carbon taken initially be ‘a’ and ‘b’
respectively.
CaCO3(s) CaO(s) + CO2(g)
Moles at equilibrium a x x (x y)
CO2(g) + C(s) 2CO(g)
Moles at equilibrium (x y) (b y) 2y
Thus, as CO2 is common in both the equilibrium so its concentration is same in both the
equilibrium constant expressions.
Equilibrium constant for first equilibrium, 1
C
K = [CO2] =
V
y
x
Equilibrium constant for second equilibrium, 2
C
K =
2
2
CO
CO
=
)
y
V
V
2
(
2
(x
y)2
=
y)
V(x
4y2
POINTS TO BE REMEMBERED FOR WRITING EQUILIBRIUM CONSTANT EXPRESSIONS
The concentration of the reacting species in the solution phase is expressed in mol/litre.
The concentration of the reacting species in the gaseous phase can be expressed either in mol/litre
or in atm.
The concentration of pure solid, pure liquids (in heterogeneous equilibria) and solvents
(in homogeneous equilibria) are constant and do not appear in the equilibrium constant expression
of a reaction.
Kp and Kc are related as, Kp = Kc(RT)n
where n = number of moles of gaseous product number
of moles of gaseous reactant.
It is not customary to write units of equilibrium constants (Kp and Kc) but when mentioned, the
units of Kp are (atm)n
and units of Kc are .
litre
moles
n
In quoting the value of equilibrium constant, we must specify the balanced equation and the
temperature at which equilibrium is established.
If a reaction can be expressed as the sum of two or more reactions, the product of the equilibrium
constants of the individual reactions gives the equilibrium constant for the overall reaction.
SIMULTANEOUS EQUILIBRIA
11](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-22-2048.jpg)




![All right copy reserved. No part of the material can be produced without prior permission
Since n = 0, there is no effect on changing the pressure. High temperature favours forward
reaction.
Dissociation of PCl5
PCl5(g) PCl3(g) + Cl2(g) ; H = +ve
Conditions favourable for forward reactions are (i) low pressure, (ii) high temperature. Oxidation
of carbon monoxide by steam:
CO(g) + H2O(g) CO2(g) + H2(g) ; H = –ve
n = 0 and so pressure has no effect. Low temperature favours forward reaction and so by
employing excess of steam.
Illustration 10
Question:For the gaseous equilibrium at high temperature,
PCl5(g) PCl3(g) + Cl2(g); H = 87.9 kJ
explain the effect upon the material distribution of (a) increased temperature (b)
increased pressure (c) higher concentration of Cl2 (d) higher concentration of PCl5 and
(e) presence of a catalyst.
Solution:(a) When the temperature of a system in equilibrium is raised (by addition of heat), the
equilibrium is displaced in the direction which absorbs heat. Hence increasing the
temperature will cause more PCl5 to dissociate.
(b) When the pressure of a system in equilibrium is increased, the equilibrium is displaced in the
direction of the smaller volume. One volume each of PCl3 and Cl2, a total of 2 gas volumes
(on the product side) from only 1 volume of PCl5. Hence a pressure increase will promote
the reaction to form more PCl5.
(c) Increasing the concentration of any component will displace the equilibrium in the direction
which tends to lower the concentration of the component added. Increasing the concentration
of Cl2 will result in the consumption of more PCl3 and the formation of more PCl5 and this
action will tend to offset the increased concentration of Cl2.
(d) Increasing the concentration of PCl5 will result in the formation of more PCl3 and Cl2 or
more dissociation of PCl5.
(e) A catalyst accelerates both forward and backward reactions equally. It speeds up the
approach to equilibrium but does not favor reaction in either direction.
The relation between vapour density and the degree of dissociation can be established only for a
gaseous equilibrium whose KP exists. For example,
A(g) nB (g)
Initial conc. c 0
Conc. at equilibrium c(1 ) nc
Total concentration at equilibrium = c c + nc = c [1 + n] = c [1 + (n – 1)]
Assuming that all the gaseous components at equilibrium behave ideally, we can apply ideal gas
equation.
RT
M
w
nRT
PV
P
RT
P
RT
V
w
M
V.D =
P
2
RT
….(i) [since molar mass = 2 V.D]
RELATION BETWEEN VAPOUR DENSITY AND DEGREE OF DISSOCIATION
13](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-27-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
As pressure of the system is given by,
V
nRT
P , so putting the value of P in equation (i) gives
V.D =
n
2
V
V
nRT
2
RT
where is the density of the gas or gaseous mixture expressed in g/litre.
If the equilibrium reaction is established in a closed vessel, then vapour density will be inversely
proportional to the number of moles of the gaseous species as the density of the gaseous mixture () is a
constant.
reactant
gaseous
of
moles
Initial
m
equilibriu
at
gases
of
moles
Total
m
equilibriu
at
density
Vapour
density
vapour
Initial
Let the initial vapour density and vapour density at equilibrium be ‘D’ and ‘d’ respectively, then
for the given equilibrium
c
)]
1
n
(
1
[
c
d
D
or )]
1
n
(
1
[
d
D
or )
1
n
(
1
d
D
d
n
d
D
)
1
(
)
(
where ‘n’ represents the number of moles of gaseous product given by 1 mole of the gaseous reactant.
Knowing D, d and n, the degree of dissociation () can be calculated.
The vapour density measurement is used for the determination of degree of dissociation of only
those equilibria in which 1 mole of the gaseous reactant gives more than one mole of gaseous products.
Because when one mole of the gaseous reactant gives only one mole of gaseous product, then ‘D’ and ‘d’
would be same and ‘’ can not be determined.
As you might be aware, every process in nature occurs in order to reduce the energy of a system.
This is because reduced energy state has fewer tendencies to undergo change thereby it brings stability.
When an object falls from a certain height, the process reduces the potential energy of the system. Where
as, if the object is to be taken to a certain height the potential energy increases. That’s why the former
occurs on its own, while for the latter work has to be done.
Chemical reactions too occur with decrease in energy. One might of course wonder how does an
endothermic reaction occur? Well, even endothermic reactions occur with decrease in energy! This
statement may contradict the very definition of endothermic reactions. Not so if you read on.
The energy that decreases in a chemical reaction, which brings about stability, is called Free
Energy. It is the decrease in free energy that causes a reaction to happen. For endothermic reactions also,
the free energy decreases, even though the total energy increases. This can be understood by figuring out
what is free energy?
Free energy of a system, say for example a molecule like CH4, is the total intrinsic electrostatic
potential energy of the system. In a CH4 molecule, there are in total 10 protons
(6 of C and 1 each of H) and 10 electrons (6 of C and 1 each of H). If we were to calculate the total
electrostatic potential energy of the system by calculating the potential energy of all charges due to all
other charges and adding the sum, the result would be the free energy of CH4 molecule.
For this, one needs to know the distance between all the charges, which is not practically possible. But the
concept of free energy is very useful to understand the direction of reactions. Free energy represents the
RELATION BETWEEN FREE ENERGY CHANGE & EQUILIBRIUM CONSTANT
14](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-28-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
stability of a system. Lower the value of free energy; more are the attractive forces in the system and
consequently more is the stability. If one were to ask why methane is a tetrahedron then a safe answer
would be that it is the tetrahedral shape that allows methane to have the least possible free energy. With
temperature free energy is likely to change as bond distances and angles may get altered.
Let us consider a reaction,
A + B C + D
Free Energy per mole 3 6 2 5
(in kJ)
No. of mole 2 3 4 1
If we look at this reaction we can see that the total Free Energy on the left is
[2 (3)] + [3 (6)] = 24. On the other hand, the free energy on the right side is [4 (2)] + [1 (5)] = 13.
This means that the left side of the reaction has greater instability than the right side. So to bring about
stability, the free energy lowers itself by moving the reaction to the forward direction. The corollary of this
is that the reverse reaction does not occur because this would bring about instability. As the forward
reaction occurs the number of mole of A & B decreases while that of
C & D increases. This makes the number on the left side smaller and that of the right side bigger. Finally a
stage is reached when the free energy of the left and the right become equal. This is the stage when
equilibrium is established. At this juncture the reverse reaction starts to occur (because free energy while
going reverse is not taking the reaction to the side of instability) with the same speed as that of the forward
reaction.
Therefore, free energy change is zero when the reaction is at equilibrium (G = 0).
When the concentration of all reactants and products is 1 mole/litre, the change in Free Energy is
represented as
0
G
. For the reaction shown
0
G
= 2.
Thus, G is the free energy change at any given concentration of reactants and products.
If all the reactants and products are taken at a concentration of one mol per litre, the free energy change of
the reaction is called
0
G
(standard free energy change). Remember that
0
G
is not necessarily the free
energy change at equilibrium.
G° = 0
f
G
of products 0
f
G
of reactants
and G = Gf of products Gf of reactants.
If G = ve, reaction goes in the forward direction
G = +ve, reaction goes in the backward direction
G = 0, reaction is at equilibrium
It has been proved (proof not required) that
0
G
= RT ln K.
where T is always in Kelvin, and if R is in joules,
0
G
will be in joules, and if R is calories then
0
G
will
be in calories.
[Note: K may either be KC or KP or any other equilibrium constant. The use of this relation between
0
G
and equilibrium constant (K) will also be seen in the lesson “Electrochemistry”.]](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-29-2048.jpg)


![All right copy reserved. No part of the material can be produced without prior permission
KP =
)]
2
1
(
c
[
)]
1
(
c
[
P
c
2
c
P
P
P
2
T
2
2
2
AB
2
AB
2
B
KP =
2
1
)
1
(
2
P
2
T
3
Since, is small as compared to unity, so 1 ~ 1 and
2
1
~1.
KP =
2
PT
3
(a)
Example 6:
For the equilibrium,
H2O(s) H2O(l)
which of the following statement is true?
(a) The pressure changes do not affect the equilibrium.
(b) More of ice melts, if pressure on the system is increased.
(c) More of liquid freezes, if pressure on the system is increased.
(d) The pressure changes may increase or decrease the degree of advancement of the reaction
depending upon the temperature of the system.
Solution:
For heterogeneous physical equilibrium, with the increase of pressure, equilibrium shifts
in the direction of physical state having higher density. This means that for the equilibrium,
H2O(s) H2O(l), more ice would melt on increasing the pressure of the system as density of
water is more than ice.
(b)
Example 7:
For the reaction,
NH2COONH4(s) 2NH3(g) + CO2(g)
The equilibrium constant Kp = 2. 9 105
atm3
at T K. The total pressure of gases at
equilibrium when 1.0 mole of reactant was heated at T K will be
(a) 0.0194 atm (b) 0.0388 atm
(c) 0.058 atm (d) 0.0667 atm
Solution:
NH2COONH4(s) 2NH3(g) + CO2(g)
Moles initially 1 0 0
Moles at equib. (1 x) 2x x
Total moles of gaseous species at equilibrium = 3x
Equilibrium pressure = PT
3
P
P
,
P
3
2
P T
2
CO
T
3
NH
2
CO
2
3
NH
p P
)
P
(
K =
3
P
P
3
2 T
2
T
27
P
4
10
9
.
2
3
T
5
PT = 0.058 atm](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-32-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
(c)
Example 8:
In an equilibrium reaction, x moles of the gaseous reactant ‘A’ decompose to give 1 mole
each of gaseous ‘C’ and ‘D’. If the fraction of A decomposed at equilibrium is independent of
the initial concentration, then the value of x would be
(a) 1 (b) 2 (c) 3 (d) 4
Solution:
The fraction of A decomposed at equilibrium is independent of initial concentration means the
equilibrium constant expression is free from concentration term. The equilibrium reaction is
xA(g) C(g) + D(g)
Initial conc. c 0 0
Conc. at. equil. c(1 )
x
c
x
c
KC =
x
x
x
x
)
1
(
c
c
c
A
D
C
=
x
2
x α)
c(1
c
2
The expression of KC would be free from concentration term only when value of x is 2 as the
power of concentration term in the numerator is 2.
Thus, putting x = 2, gives
2
2
2
C
α)
c(1
4
c
K
= 2
2
α)
(1
4
(b)
Example 9:
At a certain temperature the following equilibrium is established,
CO(g) + NO2(g) CO2(g) + NO(g).
One mole of each of the four gases is mixed in one litre container and the reaction is allowed
to reach equilibrium state. When excess of baryta water is added to the equilibrium mixture,
the weight of white precipitate obtained is 236.4 g. The equilibrium constant, Kc of the
reaction is
(a) 1.2 (b) 2.25
(c) 2.1 (d) 3.6
Solution:
CO(g) + NO2(g) CO2(g) + NO(g)
Moles initially 1 1 1 1
Moles at equib. 1 x 1 x 1 + x 1 + x
CO2 + Ba(OH)2 BaCO3 + H2O
Moles of BaCO3 =
197
4
.
236
= 1.2
Moles of CO2 at equilibrium = 1.2
or, 1 + x = 1.2 ; x = 0.2
25
.
2
8
.
0
2
.
1
1
1
K
2
2
c
x
x
(b)
Example 10:
The approach to the following equilibrium was observed kinetically from both directions.
[PtCl4]2
+ H2O [Pt(H2O)Cl3]
+ Cl
At 25°C, it was found that](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-33-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
Δt
PtCl
Δ
2
4
= (3.9 105
s1
) [PtCl4]2
(2.1 103
L mol1
. s1
) [Pt(H2O)Cl3]
[Cl
]
The value of Kc (equilibrium constant) for the complexation of the fourth Cl
by Pt(II) is
(a) 53.8 (b) 50 (c) 60 (d) 63.8
Solution:
At equilibrium, the rate of change of concentration of any species (reactant or product) is zero.
The equilibrium reaction for the complexation of the fourth Cl
by Pt(II) is
[Pt(H2O)Cl3]
+ [Cl
] [PtCl4]2
+ H2O
Keq =
Cl
Cl
)
O
H
(
Pt
O
H
PtCl
3
2
2
2
4
Since, water is a solvent in the given reaction, so its concentration remains constant.
O
H
K
2
eq
=
Cl
Cl
)
O
H
(
Pt
PtCl
3
2
2
4
= KC
In the problem, expression of rate of change of concentration of
2
4
PtCl is given, which at
equilibrium is zero.
t
PtCl
2
4
= (3.9 105
) [PtCl4]2
(2.1 103
) [Pt(H2O)Cl3]
[Cl
] = 0
(3.9 105
) [PtCl4]2
= (2.1 103
) [Pt(H2O)Cl3]
[Cl
]
Cl
Cl
)
O
H
(
Pt
PtCl
3
2
2
4
= KC = 5
3
10
9
.
3
10
1
.
2
= 53.8
(a)
Example 11:
Enough solid NH4HS and LiCl.3NH3 are heated in a closed vessel at 100°C and the following
equilibria are established.
LiCl.3NH3(s) LiCl.NH3(s) + 2NH3(g)
NH4HS(s) NH3(g) + H2S(g)
If Kp for the first equilibrium at 100°C is 9 atm2
and the total pressure of the system is 12
atm, then the Kp for second equilibrium would be
(a)9 atm2
(b) 27 atm2
(c)3 atm2
(d) 81 atm2
Solution:
LiCl.3NH3(s) LiCl.NH3(s) + 2NH3(g)
NH4HS(s) NH3(g) + H2S(g)
Since both equilibria are attained simultaneously, thus
2
NH3
P = 9 3
NH
P = 3 atm
3
NH
P + S
H2
P = 12
S
H2
P = 9 atm
For second equilibrium reaction,
Kp = 3
NH
P S
H2
P = 9 3 = 27 atm2
.
(b)
Example 12:](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-34-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
When 800 ml of 1 M AgNO3 solution is mixed with 127 g Cu taken in a vessel of 2 L capacity,
the equilibrium established is 2Ag+
+ Cu(s) 2Ag(s) + Cu2+
. The moles of Cu2+
at
equilibrium are 0.2. The value of equilibrium constant (Kc) would be
(a)1.25 (b)1
(c)0.5 (d)0.4
Solution:
2Ag+
+ Cu(s) 2Ag(s) + Cu2+
Moles initially 0.8 2 0 0
Moles at equilib. 0.8 2x 2 x 2x x
Kc = 2
2
]
Ag
[
]
Cu
[
= 2
V
2
8
.
0
V
x
x
= 2
)
2
(0.8 x
x
V
Kc = 2
)
4
.
0
8
.
0
(
8
.
0
2
.
0
=
4
.
0
4
.
0
8
.
0
2
.
0
= 1.
(b)
Example 13:
A reaction has Kp = 0.33 atm. On decreasing the volume of the container, the reaction would
(a) move forward to reach equilibrium (b) move reverse to reach equilibrium
(c) remain in equilibrium (d) cannot be predicted
Solution:
Kp = 0.33 atm
The unit of Kp shows that reaction is of the type nA(g) (n + 1)B(g)
and Kc =
1
n
B
V
n
n
A
n
V
= n
A
1
n
B
)
n
(
V
)
n
(
and on decreasing the volume of the container, the value of Qc increases and reaction moves in
backward direction.
(b)
Example 14:
For the equilibrium reaction 2HI(g) H2 (g) + I2(g), the degree of dissociation
(a) is constant at a given temperature
(b) depends upon the total pressure of the system
(c) depends upon the initial mole of HI
(d) none of these
Solution:
2HI(g) H2(g) + I2(g)
c
c(1 ) c/2 c/2
Kc = 2
2
2
2
)
α
1
(
c
4
α
c
= 2
2
)
α
1
(
4
α
At constant T, Kc is a constant, so will remain constant.
(a)
Example 15:
In an equilibrium mixture containing N2O4(g) and NO2(g) at a certain temperature, the NO2
is found to be 25% by volume. The molecular weight of the equilibrium mixture is](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-35-2048.jpg)



![All right copy reserved. No part of the material can be produced without prior permission
SOLVED SUBJECTIVE EXAMPLES
Example 1:
PCl5(g) PCl3(g) + Cl2(g). Calculate the moles of Cl2 produced at equilibrium when
1.00 mol of PCl5 is heated at 250°C in a vessel having a capacity of 10.0 L. At 250°C,
KC = 0.041 for this dissociation.
Solution:
The equilibrium reaction is
PCl5(g) PCl3(g) + Cl2(g)
Initial conc.
10
1
= 0.1 0 0
Conc. at equilib. 0.1 x x x
KC =
]
PCl
[
]
Cl
[
]
PCl
[
5
2
3
=
)
1
.
0
( x
x
x
= 0.041
2
)
0041
.
0
(
4
)
041
.
0
(
041
.
0 2
x = 0.047
Moles of Cl2 produced at equilibrium = 0.047 10 = 0.47
Example 2:
At 46°C, Kp for the reaction,
N2O4(g) 2NO2(g)
is 0.66 atm. Compute the percent dissociation of N2O4 at 46°C and a total pressure of
380 torr. What are the partial pressures of N2O4 and NO2 at equilibrium?
Solution:
At equilibrium, let the partial pressure of NO2 be P atm and the total pressure be PT atm. Then the
partial pressure of N2O4 would be (PT P) atm.
N2O4(g) 2NO2(g)
KP =
P
P
P
)
P
(
)
P
(
T
2
4
O
2
N
2
2
NO
PT = atm
5
.
0
760
380
0.66 =
P
5
.
0
P2
P2
+ 0.66P 0.33 = 0
Solving quadratic equation in P gives,
P = 0.332 atm.
4
O
2
N
P = 0.5 0.332 = 0.168 atm
2
NO
P = 0.332 atm
Since each mole of N2O4, which dissociates produces 2 mole of NO2, the percent dissociation of
N2O4 is given by
100
2
332
.
0
168
.
0
2
332
.
0
100
O
N
of
pressure
Initial
decreased
O
N
of
pressure
4
2
4
2
= 50%](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-39-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
Example 3:
For the gaseous reaction of XO with O2 to form XO2, the equilibrium constant at 398 K is
1.0 104
lit/mole. If 1.0 mole of XO and 2.0 mole of O2 are placed in a 1.0 L vessel and
allowed to come to equilibrium, what will be the equilibrium concentration of each of the
species?
Solution:
The equilibrium reaction is
2XO(g) + O2(g) 2XO2(g)
since the unit of Kc given is lit/mole.
2XO(g) + O2(g) 2XO2(g)
Initial conc.
V
1
V
2
0
Conc. at equilib.
V
2
1 x
V
2 x
V
2x
KC =
2
)
2
1
(
V
4
V
2
V
2
1
V
2
]
O
[
]
XO
[
]
XO
[
2
2
2
2
2
2
2
x
x
x
x
2
1 104
=
2
)
2
1
(
1
4
2
x
x2
Since, the value of equilibrium constant is very small (1 104
), so 2x can be ignored with respect to 1.
1 2x ~ 1
1 104
= 2
4 2
x
x = 7.07 103
We can see that the value of x is very small, so the assumption made was correct as it is within
1.4% of the actual value. Thus, the assumption made is correct and acceptable.
[XO] = 1 0.01414 = 0.985 M
[O2] = 2 0.00707 = 1.992 M
[XO2] = 0.0141 M
Example 4:
At a certain temperature, the equilibrium constant for the gaseous reaction of CO with O2 to
produce CO2 is 5.0 103
lit/mole. Calculate [CO] at equilibrium, if 1.0 mol each of CO and
O2 are placed in a 2.0 L vessel and allowed to come to equilibrium.
Solution:
The equilibrium reaction would involve 2 moles of CO, 1 mole of O2 and 2 moles of CO2 as the
unit of KC is lit/mole.
So the equilibrium equation is
2CO(g) + O2(g) 2CO2(g)
The equation, CO(g) + ½ O2(g) CO2(g) would have an equilibrium constant with units
(lit/mole)1/2
.
2CO(g) + O2(g) 2CO2(g)
Initial conc.
2
1
= 0.5
2
1
= 0.5 0
Conc. at equilib. 0.5 x 0.5
2
x
x](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-40-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
KC =
]
O
[
]
CO
[
]
CO
[
2
2
2
2
= 5 103
5 103
=
2
5
.
0
)
5
.
0
( 2
x
x
x2
Since, the value of equilibrium constant is pretty high so we can assume that almost entire CO goes
to CO2. Thus, value of x would be close to 0.5. But concentration of CO, (0.5 x) would not be
zero but would be a small value. Let this value be y. Then the concentration of O2 at equilibrium
would be
2
y
25
.
0 .
5 103
=
2
y
25
.
0
y
)
5
.
0
(
2
2
As value of y is very small,
2
y
can be easily ignored with respect to 0.25.
5 103
=
25
.
0
y
)
5
.
0
(
2
2
y = 1.4 102
[CO] = y = 1.4 102
M
Example 5:
In a study of the gaseous reaction,
A(g) + 2B(g) 2C(g) + D(g),
A and B are mixed in a reaction vessel kept at 25C. The initial concentration of B is 1.5
times the initial concentration of A. After the equilibrium has been established, the
equilibrium concentrations of A and D were equal. Calculate the equilibrium constant at
25C.
Solution:
Let the initial mole of A be 1, so the initial moles of B would be 1.5.
Let x moles of A reacted at equilibrium and ‘V’ be the total volume of the system.
A(g) + 2B(g) 2C(g) + D(g)
At equilibrium (1 – x) (1.5 – 2x) 2x x
At equilibrium, [A] = [D], 1 – x = x, 1 = 2x; x =
1
2
KC = 2
2
2
2
2
1
2
1
2
1
1
]
B
[
]
A
[
]
D
[
]
C
[
= 4
Example 6:
In a mixture of N2 and H2 in molar ratio of 1: 3 at 30 atm and 300°C, the percentage of
ammonia by volume under the equilibrium is 17.8. Calculate the equilibrium constant (Kp)
for the reaction,
N2(g) + 3H2(g) 2NH3(g)
Solution:
Let the initial number of moles of N2 and H2 be 1 and 3 respectively. (This assumption is valid as
Kp will not depend on the exact number of moles of N2 and H2, taken initially. One can start even
with x and 3x).](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-41-2048.jpg)


![All right copy reserved. No part of the material can be produced without prior permission
Amount of ethanol at equilibrium = 46
3
1
1
= 30.67 g
Amount of ester at equilibrium = 88
3
1
1
= 117.33 g
And amount of water at equilibrium = 18
3
1
1
= 24 g
Example 9:
In a vessel, two equilibrium are simultaneously established at the same temperature
as follows,
N2(g) + 3H2(g) 2NH3(g) …..(1)
N2(g) + 2H2(g) N2H4(g) .….(2)
Initially the vessel contains N2 and H2 in the molar ratio of 9 : 13. The equilibrium pressure is
7P0, in which pressure due to ammonia is P0 and due to hydrogen is 2P0. Find the values of
equilibrium constants (KP’s) for both the reactions.
Solution
Let the initial pressure of N2 and H2 is 9P and 13P respectively.
N2(g) + 3H2(g) 2NH3(g)
9P – x – y 13P – 3x – 2y 2x
N2(g) + 2H2(g) N2H4(g)
9P – x – y 13P – 3x – 2y y
Pressure due to NH3 = 2x = P0
2
P0
x …..(i)
Pressure due to H2 = 13P 3x – 2y = 2P0
13P –
2
3
P0 – 2y = 2P0
13P – 2y =
2
7
P0 …..(ii)
Total pressure at equilibrium
9P x y + 13P 3x 2y + 2x + y = 7P0
9P
2
P0
+
2
P
2
P
7 0
0
= 7P0 [Putting the value from equation (i) and (ii)]
9P = 7P0
2
5
P0
9P =
2
9
P0
P =
2
P0
Inserting the value of P in equation (ii) gives
2
P
7
y
2
2
P
13 0
0
2
P
3
y 0
](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-44-2048.jpg)

![All right copy reserved. No part of the material can be produced without prior permission
A sample of air consisting of N2 and O2 was heated to 2500 K until the equilibrium
N2(g) + O2(g) 2NO(g)
was established with an equilibrium constant KC = 2.1 103
. At equilibrium, the mole % of
NO was 1.8. Estimate the initial composition of air in terms of mole fraction of N2 and O2.
Solution
N2(g) + O2(g) 2NO(g)
Initial moles a (100 a) 0
Final moles (a – x) (100 a – x) 2x
Given
100
2x
=
100
8
.
1
x = 0.9
Also, KP = KC =
]
O
[
]
N
[
]
NO
[
2
2
2
=
)
a
100
(
)
a
(
)
2
( 2
x
x
x
= 2.1 103
a = 79% ; (100 a) = 21%.
Example 12:
The degree of dissociation of HI at a particular temperature is 0.8. Calculate the volume of
2 M Na2S2O3 solution required to neutralise the iodine present in a equilibrium mixture of a
reaction when 2 mole each of H2 and I2 are heated in a closed vessel of 2 litre capacity and the
equilibrium mixture is freezed.
Solution
2HI(g) + H2(g) + I2(g)
Before dissociation 1 0 0
After dissociation (1 – )
2
2
KC = 2
2
)
1
(
4
= 2
2
)
8
.
0
1
(
4
)
8
.
0
(
= 4 (since, = 0.8)
Now, H2(g) + I2(g) 2HI(g)
Initial moles 2 2 0
Moles after reaction (2 – x) (2 – x) 2x
C
K =
C
K
1
= 2
2
)
2
(
)
2
(
x
x
or 2
2
)
2
(
)
2
(
x
x
=
4
1
;
x
x
2
2
=
2
1
or x =
5
2
Thus, moles of I2 left =
5
2
2 =
5
8
Equivalents of Na2S2O3 = Equivalents of I2 left at equilibrium (where V is the volume in L)
2 V =
5
8
2
V = 1.6 litre.
Example 13:
The activation energy of H2(g) + I2(g) 2HI(g) in equilibrium for the forward reaction
is 167 kJ mol1
whereas for the reverse reaction is 180 kJ mol1
. The presence of catalyst
lowers the activation energy by 80 kJ mol1
. Assuming that the reactions are made at 27°C
and the frequency factor for forward and backward reactions are 4 104
and 2 103
respectively, calculate KC.](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-46-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
Solution
A catalyst lowers the activation energy for forward reaction as well as for backward reaction by
equal amount.
Thus, in presence of catalyst,
Energy of activation for forward reaction )
E
( 1
a = 167 80 = 87 kJ mol1
Energy of activation for backward reaction )
E
( 2
a = 180 80 = 100 kJ mol1
For forward reaction, k1 =
RT
/
E
1
1
a
e
A
For backward reaction, k2 =
RT
/
E
2
2
a
e
A
where A1 and A2 are frequency factors and 1
a
E and 2
a
E are energies of activation after addition of
catalyst.
KC =
2
1
k
k
=
]
)
RT
/
E
(
)
RT
/
E
(
[
2
1 2
a
1
a
e
A
A
=
RT
E
E
2
1
1
a
2
a
e
.
A
A
=
3
4
10
2
10
4
300
10
314
.
8
)
87
100
(
3
e
The difference of )
E
E
( 1
2 a
a can also be taken before the addition of catalyst.
KC = 2 ]
)
10
300
314
.
8
/(
13
[
1 3
e
10
KC = 36.8.
Example 14:
For the equilibrium,
LiCl.3NH3(s) LiCl.NH3(s) + 2NH3(g), Kp = 9 atm2
at 40°C. A 5 litre vessel contains 0.1 mole of LiCl.NH3(s). How many moles of NH3 should be
added to the flask at this temperature to drive the backward reaction to completion?
Solution
LiCl.3NH3(s) LiCl.NH3(s) + 2NH3(g) ; Kp = 9 atm2
LiCl.NH3(s) + 2NH3(g) LiCl.3NH3(s) ; 1
p
K = 2
)
atm
(
9
1
Initial moles 0.1 a
Final moles at equilib. 0 (a 0.2) 0.1
Let the initial mole of NH3 be ‘a’ to bring in completion of reaction.
At equilibrium, 1
p
K = 2
NH )
P
(
1
3
;
9
1
= 2
NH )
P
(
1
3
3
NH
P = 3 atm
3
NH
P V= nRT
3 5 = n 0.0821 313 ; n = 0.5837
Total moles at equilibrium = (a 0.2) = 0.5837
Initial mole of NH3 = a = (0.5837 + 0.2) = 0.7837 mole.
Example 15:
Under what pressure conditions CuSO4.5H2O(s) be efflorescent at 25°C? How good a drying
agent is CuSO4.3H2O(s) at the same temperature? Given:
CuSO4.5H2O(s) CuSO4.3H2O(s) + 2H2O()
Kp = 1.086 104
atm2
at 25°C and vapour pressure of water at 25°C is 23.8 mm of Hg.
Solution
An efflorescent salt is the one that loses H2O when brought in contact with the atmosphere.
For the reaction,
CuSO4.5H2O(s) CuSO4.3H2O(s) + 2H2O()
Kp = 2
O
H )
P
( 2
= 1.086 104
O
H2
P = 1.042 102
atm = 7.92 mm Hg](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-47-2048.jpg)

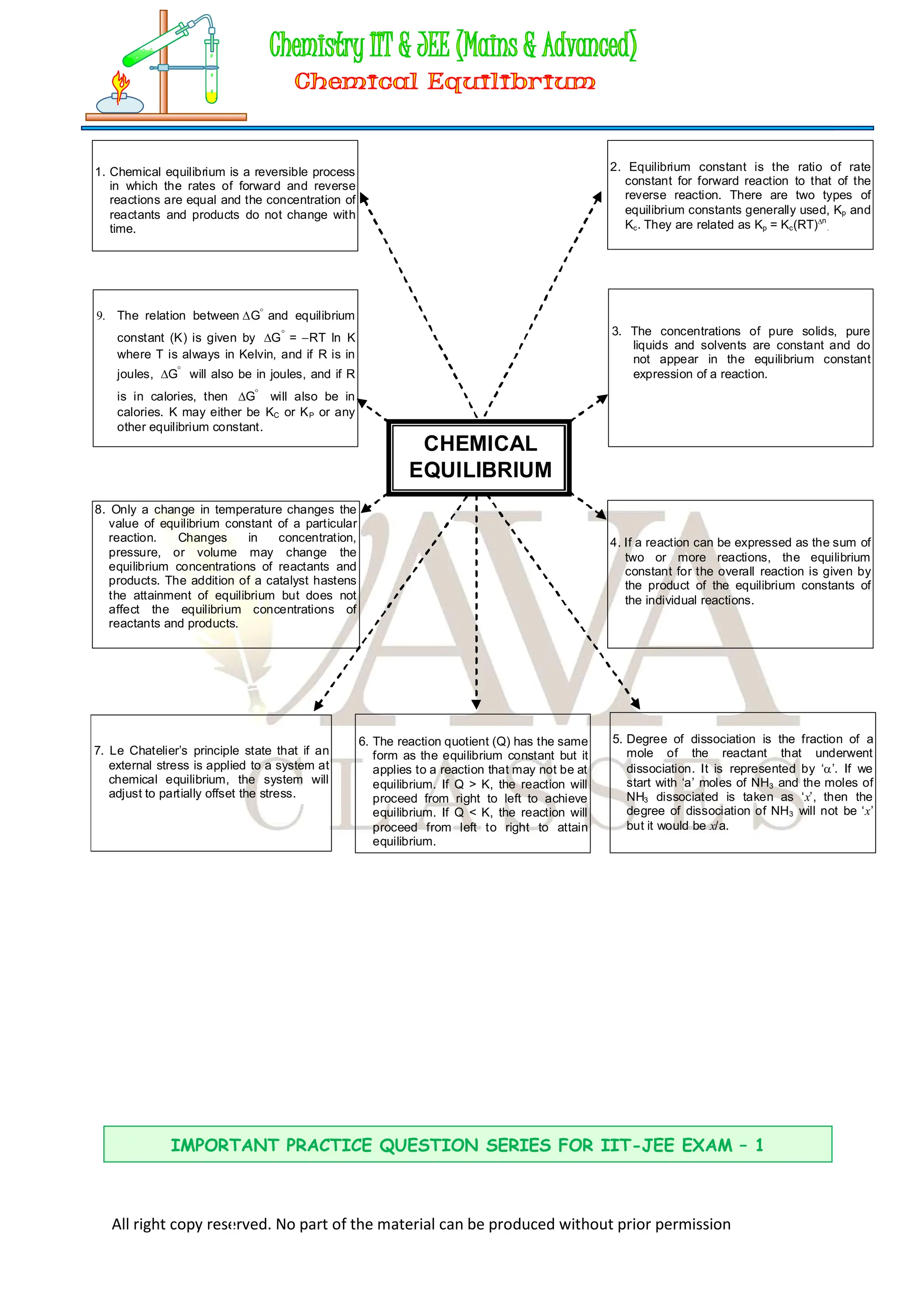
![All right copy reserved. No part of the material can be produced without prior permission
1. Which may be added to one litre of water to act as a buffer?
a) One mole of HC H O and one mole of HCl
b)One mole of NH OH and one mole of NaOH
c) One mole of NH Cl and one mole of HCl
d)One mole of HC H O and 0.5 mole of NaOH
2. An aqueous solution of 1 M NaCl and 1 M HCl is
a) not a buffer but pH < 7 b) not a buffer but pH > 7
c) a buffer with pH < 7 d) a buffer with pH > 7
3. In the following reversible reaction,
2SO + O ⇌ 2SO + 𝑄 cal
Most suitable condition for the higher production of SO is
a) Low temperature and high pressure b)Low temperature and low pressure
c) High temperature and high pressure d)High temperature and low pressure
4. Select the p𝐾 value of the strongest acid from the following
a) 1.0 b)3.0 c) 2.0 d)4.5
5. The pH of a 0.1 M solution of NH OH (having 𝐾 = 1.0 × 10 ) is equal to
a) 10 b)6 c) 11 d)12
6. In the reaction, H (g) + Cl (g) ⇌ 2HCl(g)
a) 𝐾 ≠ 𝐾 b) 𝐾 = 𝐾 c) 𝐾 > 𝐾 d) 𝐾 < 𝐾
7. The total number of different kind of buffers obtained during the titration of H PO with NaOH
are:
a) 3 b)1 c) 2 d)Zero
8. Which will not affect the degree of ionisation?
a) Temperature b)Concentration c) Type of solvent d)Current
9. Which of the following has highest pH?
a) M
4
KOH
b) M
4
NaOH
c) M
4
NH OH
d) M
4
Ca(OH)
10. Solubility product constant [𝐾 ] of salts of types 𝑀𝑋, 𝑀𝑋 and𝑀 𝑋 at temperature ‘𝑇’
are 4.0 × 10 , 3.2 × 10 and 2.7 × 10 respectively. Solubilities (mol, dm ) of the
salts at temperature ‘𝑇’ are in the order
a) 𝑀𝑋 > 𝑀𝑋 > 𝑀 𝑋 b) 𝑀 𝑋 > 𝑀𝑋 > 𝑀𝑋 c) 𝑀𝑋 > 𝑀 𝑋 > 𝑀𝑋 d) 𝑀𝑋 > 𝑀 𝑋 > 𝑀𝑋](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-50-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
11. Which of the following base is weakest?
a) NH OH; 𝐾 = 1.6 × 10 b) C H NH ; 𝐾 = 3.8 × 10
c) C H NH ; 𝐾 = 5.6 × 10 d) C H N; 𝐾 = 6.3 × 10
12. One litre of water contains 10 mole H ions. Degree of ionisation of water is:
a) 1.8 × 10 % b)1.8 × 10 % c) 3.6 × 10 % d)3.6 × 10 %
13. A precipitate is formed when
a) The ionic product is nearly equal to the solubility product
b)A solution becomes saturated
c) The ionic product exceeds the solubility product
d)The ionic product is less than solubility product
14. The precipitation is noticed when an aqueous solution of HCl is added to an aqueous solution of:
a) NaNO b)Ba(NO ) c) ZnSO d)HgNO
15. Which of the following is not a Lewis base?
a) NH b) H O c) AlCl d)None of these
16. Solubility of BaF in a solution of Ba(NO ) will be represented by the concentration term
a) [Ba ] b)[F ] c) 1
2
[F ] d)2[NO ]
17. Which of the following is a buffer?
a) NaOH + CH COOH b)NaOH + Na SO c) K SO + H SO d)NH OH + NaOH
18. For the following three reactions I, II and III, equilibrium constants are given
I. CO(g) + H O(g) ⇌ CO (g) + H (g); 𝐾
II. CH (g) + H O(g) ⇌ CO(g) + 3H (g); 𝐾
III. CH (g) + 2H O(g) ⇌ CO (g) + 4H (g); 𝐾
Which of the following relations is correct?
a) 𝐾 𝐾 = 𝐾 b) 𝐾 𝐾 = 𝐾 c) 𝐾 = 𝐾 𝐾 d) 𝐾 𝐾 = 𝐾
19. 0.1 mole of N O (g) was sealed in a tube under one atmospheric conditions at 25℃. Calculate
the number of moles of NO (g) present, if the equilibrium N O (g) ⇌ 2NO (g)(𝐾 = 0.14) is
reached after some time
a) 0.036 b)36.00 c) 360.0 d)3.600
20. A buffer solution is prepared by mixing 0.1 M ammonia and 1.0 M ammonium chloride.
At 298 K, the p𝐾 of NH OH is 5.0.The pH of the buffer is](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-51-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
a) 10.0 b)9.0 c) 6.0 d)8.0
21. Which of the following molecules acts as a Lewis acid?
a) (CH ) N b)(CH ) B c) (CH ) O d)(CH ) P
22. Which among the following is an electron deficient compound?
a) NF b) PF c) BF d) AsF
23. Identify the correct order of acidic strength of CO , CuO, CaO, H O:
a) CaO < 𝐶𝑢𝑂 < H O < 𝐶O
b)H O < 𝐶𝑢𝑂 < 𝐶𝑎𝑂 < H O
c) CaO < H O < 𝐶𝑢𝑂 < 𝐶O
d)H O < 𝐶O < 𝐶𝑎𝑂 < 𝐶𝑢𝑂
24. Which of the following is a strong acid?
a) HClO b)HBrO c) HIO d)HNO
25. According to Arrhenius concept the, strength of an acid depends on:
a) Hydrolysis
b)Concentration of acid
c) H ions furnished by acid
d)Number of mole of base used for neutralization
26. H + I ⇌ 2HI
In the above equilibrium system, if the concentration of the reactants at 25℃ is increased, the
value of 𝐾 will
a) Increase b)Decrease
c) Remains the same d)Depends on the nature of the reactants
27. 0.04 g of pure NaOH is dissolved in 10 litre of distilled water. The pH of the solution is:
a) 9 b)10 c) 11 d)12
28. What is the equilibrium expression for the reaction, P (𝑠) + 5O (g) ⇌ P O (𝑠)?
a) 𝐾 =
1
[O ]
b)𝐾 = [O ] c) 𝐾 =
[P O ]
5[P ][O ]
d)𝐾 =
[P O ]
[P ][O ]
29. When 10 mole of HCl is dissolved in one litre of water, the pH of the solution will be:
a) 8 b)7 c) Above 8 d)Below 7](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-52-2048.jpg)

![All right copy reserved. No part of the material can be produced without prior permission
39. In the reactions, PCl ⇌ PCl + Cl , the amounts of PCl , PCl and Cl at equilibrium are 2 mole
each and the total pressure is 3 am. The equilibrium constant 𝐾 is :
a) 1.0 atm b)2.0 atm c) 3.0 atm d)6.0 atm
40. Which of the following is correct for the reaction?
N (g) + 3H (g) ⇌ 2NH (g)
a) 𝐾 = 𝐾
b) 𝐾 < 𝐾
c) 𝐾 > 𝐾
d)Pressure is required to predict the correlation
41. The graph relates ln 𝐾 𝑣𝑠 for a reaction. The reaction must be :
a) Exothermic
b)Endothermic
c) ∆𝐻 is negligible
d)Highly spontaneous at ordinary temperature
42. 0.1 millimole of CdSO are present in 10 mL acid solution of 0.08 𝑁HCl. Now H S is passed to
precipitate all the Cd ions. The pH of the solution after filtering off precipitate, boiling of H S
and making the solution 100 mL by adding H O is:
a) 2 b)4 c) 6 d)8
43. Calculate the pH of a solution in which hydrogen ion concentration is 0.005 g-equi/L?
a) 2.3 b) 2.8 c) 2.9 d) 2.6
44. In 1L saturated solution of AgCl [𝐾 (AgCl)1.6 10 ], 0.1 mole of CuCl [𝐾 (CuCl)1.0 10 ]
is added. The resultant concentration of Ag in the solution is 1.6 10 . The value of ′𝑥′ is
a) 3 b)5 c) 7 d)9
45. Eight mole of a gas 𝐴𝐵 attain equilibrium in a closed container of volume 1 dm as, 2𝐴𝐵 ⇌
𝐴 (g) + 3𝐵 (g). If at equilibrium 2 mole of 𝐴 are present then, equilibrium constant is :](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-54-2048.jpg)

![All right copy reserved. No part of the material can be produced without prior permission
53. N (g) + 3H (g) ⇌ 2NH (g)
In the reaction given above, the addition of small amount of an inert gs at constant
pressure will shift the equilibrium towards which side?
a) LHS (Left hand side) b)RHS(Right hand side)
c) Neither side d)Either side
54. Which one is hard base?
a) Ag b)Cr c) I d)F
55. Which species acts as an acid and also a conjugate base of another acid?
a) HSO b)CO c) SO d)H O
56. Predict the conditions for forward reaction on the basis of Le-Chatelier’s principle for :
2SO (g) + O (g) ⇌ 2SO (g); ∆𝐻 = −198 kJ.
a) Lowering the temperature and increasing pressure
b)Any value of temperature and pressure
c) Lowering of temperature as well as pressure
d)Increasing temperature as well as pressure
57. The solubility of AgCl in water at 10℃ is 6.2 × 10 mol/litre. The 𝐾 of AgCl is:
a) [6.2 × 10 ] / b)6.2 × (10 ) c) (6.2) × 10 d)[6.2 × 10 ]
58. When pressure is applied to the equilibrium system ice r water. Which of the following
phenomenon will happen?
a) More ice will be formed b)Water will evaporate
c) More water will be formed d)Equilibrium will not be formed
59. At constant temperature in one litre vessel, when the reaction,
2SO (g) ⇌ 2SO (g) + O (g) is at equilibrium, the SO concentration is 0.6 𝑀, initial
concentration of SO is 1𝑀. The equilibrium constant is :
a) 2.7 b)1.36 c) 0.34 d)0.675
60. When 20g of CaCO were put into 10 litre flask and heated to 800C, 35% of CaCO remained
unreacted at equilibrium. 𝐾 for decomposition of CaCO is :
a) 1.145 atm b)0.145 atm c) 2.145 atm d)3.145 atm
61. For the reaction equilibrium,
2NOBr(g) ⇌ 2NO(g) + Br (g), if 𝑃 = at equilibrium and 𝑃 is total pressure. The ratio 𝐾 /𝑃
is equal to:
a) 1/9 b)1/81 c) 1/27 d)1/3](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-56-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
62. 𝐾 = 1.2 × 10 of 𝑀 SO (𝑀 is monovalent metal ion) at 298 K. The maximum concentration
of 𝑀 ions that could be attained in a saturated solution of this solid at 298 K is:
a) 3.46 × 10 𝑀 b)7.0 × 10 𝑀 c) 2.88 × 10 𝑀 d)14.4 × 10 𝑀
63. Which of the following describes correct sequence for decreasing Lewis acid nature?
a) BCl > 𝐵F > 𝐵𝐵r b)BBr > 𝐵𝐶l > 𝐵F c) BBr > 𝐵F > 𝐵𝐶l d)BF > 𝐵𝐶l > 𝐵𝐵r
64. What should be the pH of solution to dissolve the Cr(OH) precipitate?
[Given, [Cr ] = 1.0 mol L
⁄ , 𝐾 = 6 × 10 )
a) 2.0 b)3.0 c) 5.0 d)4.0
65. Which one of the following salts on being dissolved in water gives pH>7 at 25℃?
a) KCN b) KNO c) NH Cl d) NH CN
66. Aqueous solution of which salt has the lowest pH?
a) NaOH b)NH Cl c) Na CO d)NaCl
67. In a gaseous reversible reaction,
N + O ⇌ 2NO + heat
If pressure is increased then the equilibrium constant would be
a) Unchanged
b)Increased
c) Decreased
d)Sometimes increased, sometimes decreased
68. Glycine is:
a) Arrhenius acid b)Lewis base c) Simplest amino acid d)All of these
69. On a given condition, the equilibrium concentration of HI, H and I are 0.80, 0.10 and 0.10
mol/L. The equilibrium constant for the reaction, H + I ⇌ 2HI, will be
a) 8 b)16 c) 32 d)64
70. If pH of the solution is one, what weight of HCl present in one litre of solution?
a) 3.65 g b)36.5 g c) 0.365 g d)0.0365 g
71. The concentration of hydroxyl ion in a solution left after mixing 100 mL of 0.1 𝑀MgCl and
100 mL of 0.2 𝑀NaOH 𝐾 of Mg(OH ) = 1.2 × 10 is:
a) 2.8 × 10 b)2.8 × 10 c) 2.8 × 10 d)2.8 × 10
72. For a reaction and equilibrium which of the following is correct?
a) Concentration of reactant=concentration of product](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-57-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
b)Concentration of reactant is always greater than product
c) Rate of forward reaction=rate of backward reaction
d) 𝑄 = 𝑘
73. The correct order of increasing basic nature of the given conjugate bases is:
a)
RCOO < 𝐻𝐶 ≡ C < NH < R
b)
RCOO < 𝐻𝐶 ≡ C < R < NH
c)
R < 𝐻𝐶 ≡ C < 𝑅𝐶𝑂O < NH
d)
RCOO < NH < 𝐻𝐶 ≡ C < R
74. What is the equilibrium expression for the reaction
P (𝑠) + 5O (g) ⇌ P O (𝑠) ?
a) 𝐾 =
[P O ]
[P ][O ]
b) 𝐾 =
[P O ]
5[P ][O ]
c) 𝐾 = [O ] d) 𝐾 =
1
[O ]
75. A characteristic feature of reversible reaction is that :
a) They never proceed to completion
b)They proceed to completion
c) They are not complete unless the reactants are removed from the sphere of reaction mixture
d)None of the above
76.
The concentration of CO be in equilibrium with 2.5 × 10 mol litre of COat100C for the
reaction : FeO(𝑠) + CO(g) ⇌ Fe(𝑠) + CO (g); 𝐾 = 5.0
a) 5 M b)1.25 M c) 12.5 M d)0.125 M
77. In the reaction, H + I ⇌ 2HI
In a 2 I flask 0.4 moles of each H and I are taken. At equilibrium 0.5 moles of HI are
formed. What will be the value of equilibrium constant 𝐾 ?
a) 20.2 b)25.4 c) 0.284 d)11.1
78. 0.005 M acid solution has 5 pH. The percentage ionisation of acid is
a) 0.8% b)0.6 % c) 0.4 % d)0.2 %
79. A solution of pH 8 is … basic than a solution of pH 12.
a) Less b)More c) Equally d)None of these
80. Which statement is/are correct?](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-58-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
a) All Arrhenius acids are Bronsted acids
b)All Arrhenius bases are not Bronsted base
c) H ion in solution exists as H O
d)All of the above
81. The concentration of fluroacetic acid (𝐾 of acid = 2.6 × 10 ) which is required to get [H ] =
1.50 × 10 𝑀 is:
a) 0.865 𝑀
b)2.37 × 10 𝑀
c) 2.37 × 10 𝑀
d)2.37 × 10 𝑀
82. Which among the following is the strongest acid?
a) H(ClO)O b)H(ClO)O c) H(ClO)O d)H(ClO)
83. Which one of the following is not an amphoteric substance?
a) HNO b) HCO c) H O d) NH
84. For the chemical reaction 3𝑋(g) + 𝑌(g) ⇌ 𝑋 𝑌(g), that amount of X Y at equilibrium is
affected by
a) Temperature and pressure b)Temperature only
c) Pressure only d)Temperature, pressure and catalyst
85. 𝐾 /𝐾 for the reaction,
CO(g) +
1
2
O (g) ⇌ CO (g)is:
a) 𝑅𝑇 b)
1/ √𝑅𝑇
c)
√𝑅𝑇
d)1
86. Densities of diamond and graphite are 3.5 and 2.3 g/mL respectively. Increase of pressure on
the equilibrium C ⇌ C :
a) Favours backward reaction
b)Favours forward reaction
c) Have no effect
d)Increases the reaction rate
87. The solubility product of BaCl is 4 × 10 . Its solubility in mol/L is
a) 4 × 10 b) 4 × 10 c) 1 × 10 d) 1 × 10](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-59-2048.jpg)


![All right copy reserved. No part of the material can be produced without prior permission
𝑖. 𝑒., if its 𝐾 value is large.
We know that,
p𝐾 = log
5 (c)
[OH ] = 𝐾 × C
= 1 × 10 × 10
= 10 = 10
𝐾 = [H ][OH ]
10 = [H ][10 ]
[H ] = 10
Hence, pH = − log H
= − log(1 × 10 ) = 11
6 (b)
H (g) + Cl (g) ⇌ 2HCl(g)
We know that,
𝐾 = 𝐾 . (𝑅𝑇)∆
∆𝑛 = no. of moles of gaseous products – no. of moles of gaseous reactants
=2-2=0
𝐾 = 𝐾 . (𝑅𝑇)
𝐾 = 𝐾
7 (a)
NaH PO + H PO ; NaH PO + Na HPO ; Na HPO + Na PO .
9 (d)
pH of a solution ∝ [OH ] Ca(OH) solution will give highest concentration of](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-63-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
[OH ]. Hence, it has highest pH.
10 (d)
Salt Solubility
product
Solubility
𝑀𝑋 𝑆
= 4.0 × 10
𝑆
= 2
× 10
𝑀𝑋 4𝑆
= 3.2
× 10
𝑆
= 2
× 10
𝑀 𝑋 27𝑆
= 2.7
× 10
𝑆
= 1
× 10
Thus, solubility order=𝑀𝑋 > 𝑀 𝑋 > 𝑀𝑋
11 (b)
Basic strength ∝ dissociation constant of base (𝐾 ).
So, smaller the value of 𝐾 weaker will be the base.
The weakest base will have smallest value of 𝐾 .
∵ C H NH (aniline) has smallest value of 𝐾 .
∴ It is weakest base.
12 (a)
𝛼 =
number of mole dissociated
total mole present
=
10
1000/18
= 1.8 × 10 = 1.8 × 10 %
Total mole of H O in 1 litre =
13 (c)
A precipitate is formed when the ionic product exceeds the solubility product.
i.e.,[𝐴 ][𝐵 ] > 𝐾](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-64-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
14 (d)
2HgNO + 2HCl ⟶ Hg Cl + 2HNO ;
Hg Cl in insoluble in water.
15 (c)
Lewis bases are electrons rich compounds.
(i) are Lewis bases because they have lone pair of electron.
(ii)AlCl is Lewis acid because it can accept electrons.
16 (c)
Ba(NO ) givesNO , Ba ions, hence Ba ion increases. To keep 𝐾 constant, [F ]
decreases. Thus, it is represented as [F ]
18 (c)
As equation ‘III’ is obtained on adding equation ‘I’ and equation ‘II’, so 𝐾 = 𝐾 . 𝐾 .
19 (a)
N O ⇌ 2NO
0.1 0 initialy
(0.1 − α) 2α at equilibrium
0.1 − α
0.1 + α
𝑝
2α
0.1 + α
𝑝at𝑝
𝐾 =
[NO ]
[N O ]
0.14 =
2α × 𝑝
0.1 + α
×
0.1 + α
0.1 − α
𝑝
=
4α
(0.1 + α)(0.1 − α)
𝑝
=
4α
0.01 − α
× 1
or α = 0.018
Thus, [NO ] = 2 × 0.018 = 0.036 mol
20 (d)](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-65-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
From Henderson equation
pOH = p𝐾 + log
[salt]
[base]
pH + pOH = 14
pOH = 5.0 + log
[1.0]
[0.1]
= 5 + log 10 = 5 + 1
pOH = 6
pH + pOH = 14
pH + 6 = 14
pH = 14 − 6 = 8
21 (b)
It has sextet of electron and can accept lone pair of electron.
22 (c)
BF is electron deficient compound because B has six electrons in outermost orbit. It
has incomplete octet. So,it is an electron deficient molecule.
23 (a)
Metal oxides are basic, non-metal oxides are acidic. CaO is more basic than CuO. Water
(H O) is amphoteric.
24 (a)
The acidic character of oxy-acids decreases down the group and increases along the period.
Also higher ox.no. of non-metal in oxy-acid shows more acidic nature.
25 (c)
Follow Arrhenius concept.
27 (b)
𝑁 =
0.04
40 × 10
= 10 𝑁
∴ pOH = 4
∴ pH = 10
28 (a)](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-66-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
P (𝑠) + 5O (g) ⇌ P O (𝑠)
𝐾 =
[P O (𝑠)]
[P (𝑠)][O (g)]
We know that concentration of a solid component is always taken as unity
𝐾 =
1
[O ]
29 (d)
[HCl] = 10 𝑀, Being very dilute pH < 7.
New concentration of,
HCl =
10
100
= 10 𝑀
∴ [H ] = 10 + 10
= 1.1 × 10 𝑀
∴ pH ≈ 7
30 (d)
A buffer solution is more effective in the pH range of p𝐾 ± 1.
31 (c)
From H O, [H ] = 1 × 10 M
From HCl[H ] = 1 × 10 M
Total [H ] = (1 × 10 + 1 × 10 )M
= (1 × 10 + 0.1 × 10 )M
= 1.1 × 10 M
pH = − log(1.1 × 10 ) = 6.9586
32 (b)
pH = − log 𝐾 + log
[Conjugate base]
[Acid]
33 (b)
100 mL of 0.01 M NaOH solution is diluted to 1 dm (𝑖. 𝑒., 10 times diluted hence, the](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-67-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
resultant solution will be 0.001 M)
[OH ] = 0.001 = 10
[H ] =
10
[OH ]
=
10
10
= 10
pH = − log[H ]
= − log[10 ]
pH=11
34 (a)
Only salts of (weak acid+ strong base) and (strong acid + weak base) get
hydrolysed (𝑖. 𝑒., show alkalinity or acidity in water). KClO a salt of strong acid and
strong base, therefore, it does not get hydrolysed in water.
KClO ⇌ K + ClO
35 (a)
Higher is the value of 𝐾 or 𝐾 more is feasibility for reaction to show forward reaction.
36 (d)
A +ve inductive effect of C H intensifies +ve charge on N atom and thus, availability of co-
ordination for electron pair decreases; The basic character order is
C H NH > 𝐶H NH > 𝑁H > C H − NH
37 (c)
Na HPO on hydrolysis of HPO ion produces free OH ion in solution.
38 (b)
2HI ⇌ H + I
3.2 0 0 initially](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-68-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
3.2 − 𝑥𝑥𝑥 at equilibrium
𝑥 = 22% of 3.2
=
22 × 3.2
100
= 0.704
Hence, number of moles of HI present at equilibrium
= 3.2 − 𝑥
= 3.2 − 0.704
= 2.496
40 (b)
N (g) + 3H (g) ⇌ 2NH (g)
∆𝑛 = 𝑛 − 𝑛
= 2 − 4
= −2
∴ 𝐾 = 𝐾 (𝑅𝑇)
or 𝐾 = ( )
𝐾 < 𝐾
41 (a)
𝐼𝑛
𝐾
𝐾
=
∆𝐻
𝑅
𝑇 − 𝑇
𝑇 𝑇
𝐾 increase with or decreases with 𝑇 it is decided by ∆𝐻.
Here, 𝐾 decrease with 𝑇. Thus, ∆𝐻 = −ve.
43 (a)
pH = − log[H ] = − log[0.005]
= − log[5 × 10 ] = 2.3](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-69-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
44 (c)
It is a case of simultaneous solubility of salts with a common ion. Here solubility
product of CuCl is much greater than that of AgCl, it can be assumed that Cl in
solution comes mainly from CuCl.
⇒ [Cl ] = 𝐾 (CuCl) = 10 M
Now for AgCl ∶ 𝐾 = 1.6 × 10
= [Ag ][Cl ]
= [Ag ] × 10
⇒ [Ag ] = 1.6 × 10
46 (b)
Find solubility for each separately by 𝑠 = 𝐾 for MnS and ZnS, 108𝑠 = 𝐾 for Bi S and
4 𝑠 = 𝐾 for Ag S.
47 (c)
𝐾 =
1
𝐾
=
1
2.4 × 10
= 4.2 × 10
48 (d)
Li Na (AlF ) = 3Li + 3Na + 2AlF
∴ 𝐾 = (3𝑎) (3𝑎) (2𝑎 ) = 2916a .
49 (b)
Dissociation constant
H O ⇌ H + OH : [H ] = OH = 1 × 10 M
And [H O]=1 g/mL = 1000 gL
=
1000
18
mol L = 55.56 M
𝐾 =
[H ][OH ]
H O
=
10
55.6
𝐾 = 1 × 10
So, 𝐾 = 55.6 × 𝐾](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-70-2048.jpg)

![All right copy reserved. No part of the material can be produced without prior permission
61 (b)
2NOBr(g) ⇌ 2NO + Br
6𝑃
9
2𝑃
9
𝑃
9
Total pressure = + + = P
𝐾 =
(𝑃 ) (𝑃 )
(𝑃 )
=
(2𝑃/9) (𝑃/9)
6𝑃
9
=
𝑃
81
62 (c)
𝐾 = 4𝑠
or 𝑠 =
1.2 × 10
4
/
= 1.44 × 10
∴ [𝑀 ] = 1.44 × 10 × 2
= 2.88 × 10 𝑀.
63 (b)
Due to back bonding (BF shows maximum tendency due to small size of F).
64 (c)
Cr(OH) ⇌ Cr + 3OH
For precipitate to be dissolved,
𝐾 ≤ [Cr ][OH ]
or 6 × 10 ≤ [0.1][OH ]
∴ [OH ] ≥ 1.79 × 10
So, [H ] ≤ . ×
≤ 5.59 × 10
pH ≥ − log(5.59 × 10 ) or pH ≥ 4.253
65 (a)
KCN is a salt of weak acid and strong base hence, on being dissolved in water gives
basic solution 𝑖. 𝑒., pH > 7 at 25℃ .
66 (b)](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-72-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
NH Cl is acidic due to hydrolysis of NH ;
NH + H O ⇌ NH OH + H ; pH < 7.
67 (a)
When the number of moles of gaseous reactants and products is same, then
equilibrium is not affected by pressure and hence, the equilibrium constant is
unaffected.
68 (d)
Glycine, the simplest amino acid (CH NH COOH) has the tendency to donate H by −COOH
gp. and the tendency to donate lone pair by N-atom of −NH gp. and also exists as Zwitter
ion.
H NCH ∙ COOH ⇌ H N CH COO
69 (d)
H + I ⇌ 2HI
[HI] = 0.80, [H ] = 0.10, [I ] = 0.10
𝐾 =
[HI]
[H ][I ]
=
0.80 × 0.80
0.10 × 0.10
= 64
70 (a)
[H ] = 10 𝑀
∴
𝑤
36.5
= 10
or 𝑤 = 36.5 × 10 = 3.65 g
72 (c)
At chemical equilibrium, rate of forward reaction is equal to the rate of backward
reaction.
73 (a)
Acidic nature is
𝑅COOH > 𝐶𝐻 ≡ 𝐶𝐻 > NH > 𝑅H
Stronger is acid, weaker is its conjugate base.
74 (d)
In the expression for equilibrium constant (𝐾 or𝐾 ) species in solid state are not](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-73-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
written (𝑖. 𝑒., their molar concentrations are taken as 1)
P (𝑠) + 5O (g) ⇌ P O (𝑠)
Thus, 𝐾 = [ ]
75 (a)
Reversible reaction always attains equilibrium and never go for completion.
76 (d)
𝐾 =
[CO ]
[CO]
∴ 5 =
[CO ]
2.5 × 10-
∴ [CO ] = 0.125 𝑀
77 (d)
H + I ⇌ 2HI
Initial 0.4 0.4 0
At equilibrium 0.4-0.25 0.4-0.25 0.05
=0.15 =0.15
𝐾 =
[HI]
[H ][I ]
=
0.50
2
0.15
2
0.15
2
=
0.5 × 0.5
0.15 × 0.15
= 11.11
78 (d)
We know that,
[H ] = 10 = 10
α =
actual concentration
molar concentration
=
10
0.005
= 0.2 × 10
∴Percentage ionisation = 0.2 × 10 × 100](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-74-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
= 0.2%
79 (a)
More is pH, more basic is solution.
80 (d)
Both Arrhenius and Bronsted bases are source of H Arrhenius base (OH furnish) may not
be capable of accepting proton (𝑖. 𝑒., Bronsted based). H exists as H O .
82 (b)
For oxoacids of the same element, the acidic strength increases with increase in the
oxidation number of the element
83 (a)
HNO (nitric acid) is generally not an amphoteric substance. It is a strong acid
(proton-donating) though sometimes, in presence of stronger acid, it also acts as a
base (e.g., in nitration of atomic compounds, it acts as a base and accept proton from
H SO ). However HCO , H O and NH frequently act both as an acid as well as a
base (i.e., amphoteric in nature).
85 (b)
𝐾 = 𝐾 (𝑅𝑇) /
∵∆𝑛 = −1/2
86 (c)
Le-Chatelier’s principle is not valid for solid-solid equilibrium.
87 (c)
BaCl ⟶ Ba + 2Cl
Let the solubility of BaCl is𝑥 mol/L
∴ 𝐾 = [Ba ][Cl ]
= (𝑥) × (2𝑥)
= 𝑥 × 4𝑥 = 4𝑥](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-75-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
or solubility of BaCl =
( ) ⁄
=
(4 × 10 ) ⁄
4
= 10 mol/L
88 (a)
Addition of sodium acetate in acetic acid solution, due to common ion NH the
ionisation of acetic acid is supressed so concentration of [H ] decreases. Hence, pH
of solution increases.
89 (a)
AB ⇌ A + 2B
1 × 10 2 × 10
K = [1 × 10 ][2 × 10 ] = 4 × 10
91 (a)
Formation of SO (sulphur trioxide)from SO andO is accompanied by decrease in
volume. So, increase in pressure favours SO formation (also due to Le-Chatelier’s
principle).
93 (b)
[H ][OH ] = 10
[10 ][OH ] = 10
[OH ] =
10
10
= 10 mol dm
94 (c)
It is condition for chemical equilibrium.
95 (b)
Solution of CuSO is acidic due to hydrolysis of Cu ion.](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-76-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
97 (a)
[H ] = 10
[H ] = 10
Thus, increase in [H ] = = 1000 times.
98 (a)
According to Lewis acid is any species (molecule, radial or ion) that can accept an
electron pair to form a coordinate covalent bond. Thus, acid is an electron deficient
species e.g., BF , AlCl , SO and all cations etc.
Or AlCl
99 (c)
𝐾 of AgCl = (solubility of AgCl)
= (1 × 10 ) = 1 × 10
Suppose its solubility in 0.1 M NaCl is 𝑥 mol L
⁄
AgCl ⇌ Ag + Cl
𝑥𝑥
NaCl ⇌ Na + Cl
0.1M 0.1M
[Cl ] = (𝑥 + 0.1)M
𝐾 ofAgCl = [Ag ][Cl ]
= 𝑥 × (𝑥 + 0.1)
1 × 10 = 𝑥 + 0.1𝑥
Higher power of 𝑥 are neglecated
1 × 10 = 0.1𝑥
𝑥 = 1 × 10 M
100 (c)](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-77-2048.jpg)
![All right copy reserved. No part of the material can be produced without prior permission
For reaction, 2SO ⇌ O + 2SO
Here, ∆𝑛 = 3 − 2 = 1, 𝑖𝑒, +ve, thus, 𝐾 is more than 𝐾 [∵ 𝐾 = 𝐾 (𝑅𝑇)∆
]](https://image.slidesharecdn.com/chemicalequilibrium-240508121455-3fc1524e/75/Equilibrium-in-Physical-Processes-Class-11-Free-Study-Material-PDF-78-2048.jpg)