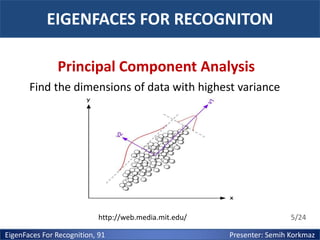
The document presents the eigenfaces method for face recognition proposed by Matthew Turk and Alex Pentland in 1991. The key steps are: (1) acquire a set of face images and calculate their eigenfaces, which are the principal components representing the significant variations between faces; (2) project the training face images into "face space" defined by the eigenfaces to train the system; (3) project new images into the same space and compare with training images to recognize faces based on Euclidean distance. Principal component analysis (PCA) is used to calculate the eigenfaces that best encode the variations between known faces.







![EIGENFACES FOR RECOGNITON
Calculate EigenFaces
• Normalize vectors.
Φ𝑖 = Γ 𝑖 − Ψ
• Form the covariance matrix
𝐴 = [Φ1 , Φ2 , . . , Φ 𝑚 ]
1
𝐶=
𝑀
𝑀
𝑇
Φ 𝑛 Φ 𝑛 = 𝐴𝐴 𝑇
𝑛=1
EigenFaces For Recognition, 91
9/24
Presenter: Semih Korkmaz](https://image.slidesharecdn.com/eigenfaces-140124151754-phpapp01/85/Eigenfaces-9-320.jpg)









![EIGENFACES FOR RECOGNITON
References
[1]Matthew Turk and Alex Pentland. 1991. Eigenfaces for recognition. J.
Cognitive Neuroscience 3, 1 (January 1991), 71-86.
DOI=10.1162/jocn.1991.3.1.71 http://dx.doi.org/10.1162/jocn.1991.3.1.71
[2]L. Sirovich and M. Kirby, Low-dimensional Procedure for the
Characterization of Human Faces, Journal of the Optical Society of
America A, 4:519--524, 1987
[3]Belhumeur, P.N.; Hespanha, J.P.; Kriegman, D., "Eigenfaces vs.
Fisherfaces: recognition using class specific linear projection," Pattern
Analysis and Machine Intelligence, IEEE Transactions on , vol.19, no.7,
pp.711,720, Jul 1997 doi: 10.1109/34.598228
22/23
EigenFaces For Recognition, 91
Presenter: Semih Korkmaz](https://image.slidesharecdn.com/eigenfaces-140124151754-phpapp01/85/Eigenfaces-22-320.jpg)
![EIGENFACES FOR RECOGNITON
References
[4] Anil K. Jain and Stan Z. Li. 2005. Handbook of Face Recognition. SpringerVerlag New York, Inc., Secaucus, NJ, USA.
23/23
EigenFaces For Recognition, 91
Presenter: Semih Korkmaz](https://image.slidesharecdn.com/eigenfaces-140124151754-phpapp01/85/Eigenfaces-23-320.jpg)
