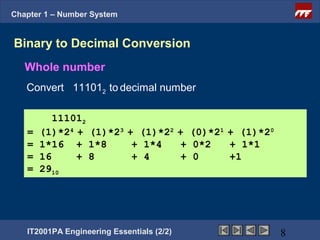
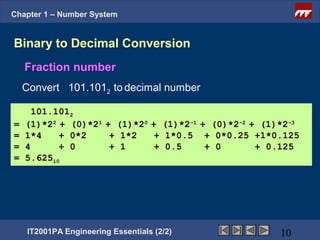
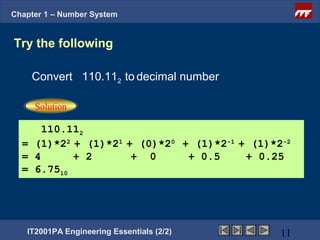
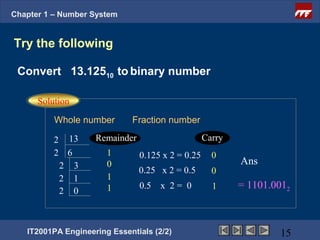
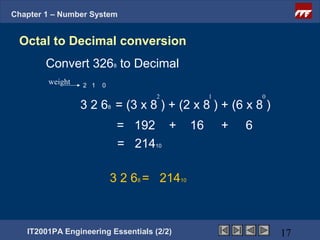
The document is a chapter from an engineering course on number systems. It discusses converting between binary, decimal, octal, hexadecimal and binary-coded decimal number systems. The objectives are to be able to convert numbers between these systems and explain their applications in digital electronics which uses binary to represent high and low voltage levels. It provides examples of converting specific numbers between the different number bases.

1. IT2001PA
Engineering Essentials (2/2)
Chapter 1 – Number System
Lecturer Name
lecturer_email@ite.edu.sg
Nov 20, 2012
Contact Number

2. Chapter 1 – Number System
Lesson Objectives
Upon completion of this topic, you should be able to:
 Convert numbers e.g. binary, octal, decimal,
hexadecimal and BCD from one system to another.
IT2001PA Engineering Essentials (2/2) 2

3. Chapter 1 – Number System
Specific Objectives
Students should be able to :
 Explain why the binary number system is ideal for digital
logic applications.
 Convert decimal whole numbers and fractional numbers into
binary numbers and vice versa.
 Convert decimal whole numbers into hexadecimal and octal
numbers and vice versa.
 Explain the term binary coded decimal.
 Convert BCD to decimal number and vice versa.
IT2001PA Engineering Essentials (2/2)

4. Chapter 1 – Number System
Application
In digital electronics,
 only deal with two voltage levels; i.e.:
 ON ≡ high or 1.
 OFF ≡ low or 0.
Therefore almost all digital systems use
 binary number system; i.e.: Base 2.
IT2001PA Engineering Essentials (2/2) 4

5. Chapter 1 – Number System
Number Systems
4 commonly used number systems:
MSB LSB
• Decimal (Base 10) 2 5
MSB LSB
• Binary (Base 2) 11001
MSB LSB
• Octal (Base 8) 3 1
MSB LSB
• Hexadecimal (Base 16) 1 9
IT2001PA Engineering Essentials (2/2) 5

6. Chapter 1 – Number System
Binary Number System
Binary number are strings of two (hence ‘bi’),
symbols 0’s and 1’s, that represent numbers.
They may be expanded in the usual way with a
base of 2.
E.g. 11012
20 1
21 0
22 4
23 8 +
1310
IT2001PA Engineering Essentials (2/2) 6

7. Chapter 1 – Number System
Binary System
 Each digit in the binary number system is called a
bit
 A group of four bits binary number is known as
Nibble.
 A group of eight bits binary number is known as
Byte.
 Two bytes number form a word.
IT2001PA Engineering Essentials (2/2) 7

8. Chapter 1 – Number System
Binary to Decimal Conversion
Whole number
Convert 111012 to decimal number
111012
= (1)*24 + (1)*23 + (1)*22 + (0)*21 + (1)*20
= 1*16 + 1*8 + 1*4 + 0*2 + 1*1
= 16 + 8 + 4 + 0 +1
= 2910
IT2001PA Engineering Essentials (2/2) 8

9. Chapter 1 – Number System
Try the following
Convert 101102 to decimal number
Solution
101102
= (1)*24 + (0)*23 + (1)*22 + (1)*21 + (0)*20
= 1*16 + 0*8 + 1*4 + 1*2 + 0*1
= 16 + 0 + 4 + 2 + 0
= 2210
IT2001PA Engineering Essentials (2/2) 9

10. Chapter 1 – Number System
Binary to Decimal Conversion
Fraction number
Convert 101.1012 to decimal number
101.1012
= (1)*22 + (0)*21 + (1)*20 + (1)*2-1 + (0)*2-2 + (1)*2-3
= 1*4 + 0*2 + 1*2 + 1*0.5 + 0*0.25 +1*0.125
= 4 + 0 + 1 + 0.5 + 0 + 0.125
= 5.62510
IT2001PA Engineering Essentials (2/2) 10

11. Chapter 1 – Number System
Try the following
Convert 110.112 to decimal number
Solution
110.112
= (1)*22 + (1)*21 + (0)*20 + (1)*2-1 + (1)*2-2
= 4 + 2 + 0 + 0.5 + 0.25
= 6.7510
IT2001PA Engineering Essentials (2/2) 11

12. Chapter 1 – Number System
Decimal to Binary Conversion
Whole number
Convert 2510 to binary number by repeated division
2 25 Remainder 2 510
2 12
12 1 LSB = 1 1 0 012
2 6 0
2 3 0
2 1 1
2 0 1 MSB
IT2001PA Engineering Essentials (2/2) 12

13. Chapter 1 – Number System
Try the following
Convert 3010 to binary number
Solution
2 30 Remainder
2 15 0
2 7 1 Ans
2 3 1
1 = 111102
2 1
2 0 1
IT2001PA Engineering Essentials (2/2) 13

14. Chapter 1 – Number System
Decimal to Binary Conversion
Fraction number
Convert 0.37510 to binary number by repeated multiplication
Carry
0.375 x 2 = 0.75 0
0.75 x 2 = 0.5 1 0.37510
0.5 x 2= 0 1 = 0.0112
IT2001PA Engineering Essentials (2/2) 14

15. Chapter 1 – Number System
Try the following
Convert 13.12510 to binary number
Solution
Whole number Fraction number
2 13 Remainder Carry
2 6 1 0.125 x 2 = 0.25 0
2 3 0 Ans
0.25 x 2 = 0.5 0
2 1 1
1 0.5 x 2= 0 1 = 1101.0012
2 0
IT2001PA Engineering Essentials (2/2) 15

16. Chapter 1 – Number System
Decimal to Octal conversion
Convert 48610 to Octal. Convert 0.61132510 to Octal.
8 | 486 Remainder Carry
8 | 60 6 LSB 0.611325 x 8 = 3.88 3 MSB
8 | 7 4 0.8906 x 8 = 7.125 6
8 | 0 7 MSB 0.125 x 8 = 1.00 1 LSB
48610 = 7468 0.61132510 = 0.3618
IT2001PA Engineering Essentials (2/2) 16

17. Chapter 1 – Number System
Octal to Decimal conversion
Convert 3268 to Decimal
weight 2 1 0
2 1 0
3 2 68 = (3 x 8 ) + (2 x 8 ) + (6 x 8 )
= 192 + 16 + 6
= 21410
3 2 68 = 21410
IT2001PA Engineering Essentials (2/2) 17

18. Chapter 1 – Number System
Decimal to Hexadecimal Conversion
Convert 49810 to Convert 0.781493710 to
Hexadecimal. Hexadecimal.
Carry
16 | 498 Remainder 0.7814937 x 16 = 12.5039 C MSB
16 | 31 2 LSB 0.5039 x 16 = 8.0624 8
16 | 1 F 0.0624 x 16 = 1.00 1 LSB
16 | 0 1 MSB
49810 = 1F216 0.781493710 = 0.C8116
IT2001PA Engineering Essentials (2/2) 18

19. Chapter 1 – Number System
Hexadecimal to Decimal conversion
Convert 2A616 to Decimal
weight
2 1 0
2 1 0
2 A 616 = (2 x 16 ) + (A x 16 ) + (6 x 16 )
= 512 + 160 + 6
= 67810
2 A 616 = 67810
IT2001PA Engineering Essentials (2/2) 19

20. Chapter 1 – Number System
Binary-Coded-Decimal System (BCD)
Used to represent each of the 10 decimal digits as
 a 4-bit binary code. Decimal BCD
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
10 0001 0000
IT2001PA Engineering Essentials (2/2) 20

21. Chapter 1 – Number System
Convert decimal number to BCD
3 5 7 9 10
0011 0101 0111 1001 (BCD)
Convert BCD to decimal number
0110 1000 0111 0011 (BCD)
6 8 7 3 10
IT2001PA Engineering Essentials (2/2) 21

22. Chapter 1 – Number System
Next Lesson
IT2001PA Engineering Essentials (2/2) 22