Certainly! Here's a comprehensive 40,000-character description on **Number Systems**, suitable for an in-depth lecture or detailed slide notes. --- ## 📘 Number Systems: Foundations, Types, Conversions, and Applications ### 1. Introduction to Number Systems A **number system** is a structured way to represent numbers using a consistent set of symbols or digits. These systems are fundamental in mathematics, computing, and digital electronics, providing the foundation for counting, calculations, data representation, and algorithm design. In everyday life, we predominantly use the **decimal system** (base 10), which employs ten digits: 0 through 9. However, in various scientific and technical fields, other number systems are utilized for their efficiency and suitability to specific applications. ### 2. 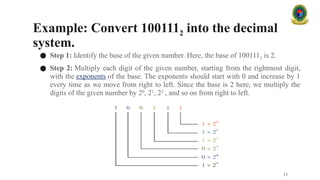Types of Number Systems #### 2.1 Decimal Number System (Base 10) The **decimal system** is the standard system for denoting integer and non-integer numbers. It is also called the base 10 system because it is based on ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. Each position in a decimal number represents a power of 10, depending on its place from the decimal point. **Example:** * The number 345.67 in decimal can be expanded as: * $3 \times 10^2 + 4 \times 10^1 + 5 \times 10^0 + 6 \times 10^{-1} + 7 \times 10^{-2}$ #### 2.2 Binary Number System (Base 2) The **binary system** uses only two digits: 0 and 1. It is the foundation of digital systems and computing, as electronic circuits have two states: on (1) and off (0). Binary numbers are used in computer memory, logic circuits, and data storage. **Example:** * The binary number 1101 represents: * $1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 = 13$ in decimal. #### 2.3 Octal Number System (Base 8) The **octal system** uses eight digits: 0 through 7. It is often used in computing as a more compact representation of binary numbers. Each octal digit corresponds to three binary digits (bits), making it easier to convert between binary and octal. **Example:** * The octal number 17 represents: * $1 \times 8^1 + 7 \times 8^0 = 15$ in decimal. 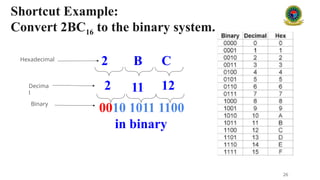#### 2.4 Hexadecimal Number System (Base 16) The **hexadecimal system** uses sixteen digits: 0 through 9 and A through F, where A represents 10, B represents 11, and so on up to F, which represents 15. Hexadecimal is widely used in computing as a more human-friendly representation of binary-coded values. **Example:** * The hexadecimal number 2F represents: * $2 \times 16^1 + 15 \times 16^0 = 47$ in decimal. #### 2.5 Other Number Systems * **Binary-Coded Decimal (BCD):** Represents each decimal digit with its binary equivalent. * **Gray Code:** A binary numeral system where two successive values differ in only one bit, used in error correction in digital communication. * **Excess-K Notation:** A binary encoding system used to represent signed numbers. 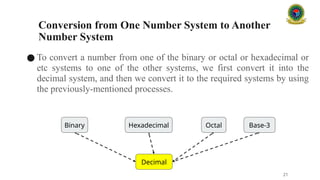### 3. Conversion Between Number Systems Converting numbers between di

1. CSE-275
Course Title: Computer Programming Language
Lec Tasnim Ullah Shakib
Lec - 3 Number Systems

2. Number System
● The number system or the numeral system is the system of naming or
representing numbers.
● We know that a number is a mathematical value that helps to count
or measure objects and it helps in performing various mathematical
calculations.
● There are different types of number systems. The 4 main are-
○ Decimal number system (Base- 10)
○ Binary number system (Base- 2)
○ Octal number system (Base-8)
○ Hexadecimal number system (Base- 16)
2

3. What is Number System?
● The value of any digit in a number can be determined by:
○ The digit
○ Its position in the number
○ The base of the number system (also called the radix value)
● Binary number system is used in computers.
○ Binary is easier for computers to process, and it also takes up less space.
○ Human logic and everything in the digital domain is inherently binary.
○ Binary system could be represented with 2 electric states– ON or OFF.
But using a number system with greater base value increases the number of
states between specified voltage range. Thus easier state transition leads to
higher chances of error, since electrical voltage levels are not steady.
3

4. Decimal Number System
● The decimal number system uses ten digits: 0,1,2,3,4,5,6,7,8 and 9 with the base
number as 10. For example, 72310, 3210, and 425710 are some examples of numbers in
the decimal number system.
● Decimal Number system is easily understandable to humans.
4

5. 5
Any positive integer N, represented in the decimal system as a string of
decimal digits, may also be expressed as a sum of powers of 10, with each
power weighted by a digit. For example, N = 8253 can be expressed as
follows :
825310 = 8×103
+2 ×102
+5 ×101
+3×100
= 8×1000+2×100+5×10+3×1
= 8000 + 200 + 50 +3
The powers of ten, which correspond respectively to the digits in a decimal
integer as read from right to left, are called the place values of the digits.
100
= 1 101
= 10 102
= 100 103
= 1000
Decimal Number System
3 2 1
0
position :
sum up all the
individual
digit x baseposition
base
or
radix
digit :

6. 6
General Number System
In generic term any whole number is expressed in radix-r system with
coefficients multiplied by powers of r.
an . rn
+ an-1 . rn-1
+………..+ a2 .r2
+a1 .r1
+ a0 .r0
The coefficients aj range in value from 0 to r – 1.

7. Binary Number System
● The binary number system uses only two digits: 0 and 1. The numbers in this system
have a base of 2. Digits 0 and 1 are called bits and 8 bits together make a byte. The
data in computers is stored in terms of bits and bytes. The binary number system does
not deal with other numbers such as 2,3,4,5 and so on. For example: 100012, 1111012,
10101012 are some examples of numbers in the binary number system.
7

8. Hexadecimal Number System
● The hexadecimal number system uses sixteen digits/alphabets: 0,1,2,3,4,5,6,7,8,9 and
A,B,C,D,E,F with the base number as 16. Here, A-F of the hexadecimal system means the
numbers 10-15 of the decimal number system respectively. This system is used in computers
to reduce the large-sized strings of the binary system. For example, 7B316, 6F16, and
4B2A16 are some examples of numbers in the hexadecimal number system.
8

9. Conversion of Number Systems
● A number can be converted from one number system to another number system using
number system formulas.
● Like binary numbers can be converted to decimal numbers and vice versa, hexadecimal
numbers can be converted to decimal numbers and vice versa, and so on.
● Number system conversion is of 3 types
○ From other bases to decimal base system.
e.g, binary to decimal, hexadecimal to decimal, base-7 to decimal, etc.
○ From decimal base system to other bases
e.g, decimal to binary, decimal to hexadecimal, decimal to base-5, etc.
○ From other bases to another base system
e.g, hexadecimal to binary, binary to hexadecimal, base-5 to base-7, etc.
Converter Link
9

10. Conversion from Other Bases to Decimal Number
System
● The steps below are used to convert a number system from the binary or
hexadecimal system or any other base to the decimal system.
Step 1: Starting with the rightmost digit, multiply each digit of the
provided number by the exponents of the base.
Step 2: Each step we take from right to left, the exponents should increase
by one, such that the exponents start with 0.
Step 3: Simplify and add each of the above-obtained products.
10

11. Example: Convert 1001112 into the decimal
system.
● Step 1: Identify the base of the given number. Here, the base of 1001112 is 2.
● Step 2: Multiply each digit of the given number, starting from the rightmost digit,
with the exponents of the base. The exponents should start with 0 and increase by 1
every time as we move from right to left. Since the base is 2 here, we multiply the
digits of the given number by 20
, 21
, 22
, and so on from right to left.
11

12. Example: Convert 1001112 into the decimal
system
● Step 3: We just simplify each of the above products and add them.
12

13. Example: Convert 110010112 into the
decimal system
110010112 = (1 × 27
) + (1 × 26
) + (0 × 25
) + (0 × 24
) + (1 × 23
) + (0 × 22
) + (1 × 21
) + (1 × 20
)
110010112 = 27
+ 26
+ 0 + 0 + 23
+ 0 + 21
+ 20
110010112 = 128 + 64 + 8 + 2 + 1
110010112 = 20310
13

14. Example:
Convert (153416)7 to a decimal number.
(153416)7
= (1 × 75
) + (5 × 74
) + (3 × 73
) + (4 × 72
) + (1 × 71
) + (6 × 70
)
= 16807 + 12005 + 1029 + 196 + 7 + 6
= (30050)10
14

15. Example:
Convert the hexadecimal number 2C4 to the
decimal number system.
Given hexadecimal number is 2C4.
As we know, the base of the hexadecimal number is 16.
Thus, 2C4 in the decimal number system is given as follows:
2C416 = (2 × 162
) + (C × 161
) + (4 × 160
)
2C416 = (2 × 256) + (12 × 16) + (4 × 1)
2C416 = 512 + 192 + 4
2C416 = 70810
Hence, the hexadecimal number 2C416 is equivalent to 70810.
15
⮚ Hexadecimal to Decimal : 2D5C16 = ( ? )10

16. Conversion from Decimal Number System to Other
Bases:
The steps below are used to change a number from the decimal number system to the
binary or hexadecimal or any number system.
Step 1: Determine the desired number’s base. For example, if we need to convert a
particular number to the binary system, the required number’s base is 2.
Step 2: In the quotient-remainder form, divide the given number by the base of the
needed number and write the quotient and remainder. Repeat the procedure until the
quotient will be 0 (by dividing the quotient by the base again).
Step 3: In the new number system, the specified number is found by writing all the
remainders from bottom to top.
16

17. Example:
Convert the number 1810 to the binary system.
Given: 1810.
Now, we have to convert the decimal system to the binary number
system. Hence, the desired number’s base is 2.
Step 1: Divide 18 by 2, we get: quotient = 9 and remainder = 0
Step 2: Divide 9 by 2, we get: quotient = 4 and remainder = 1
Step 3: Divide 4 by 2, we get: quotient = 2 and remainder = 0
Step 4: Divide 2 by 2, we get: quotient = 1 and remainder = 0
Step 5: Divide 1 by 2, we get: quotient = 0 and remainder = 1
Now, write the remainder from step 5 to step 1.
Hence, the binary equivalent of 1810 is 100102.
17
2
0 - 1

18. Example:
Convert the number 506210 to the binary system
Given: 506210.
Now, we have to convert the decimal system to
the binary number system. Hence, the desired
number’s base is 2.
18
2
0 - 1
So 5062 10 = 1001111000110 2

19. Example:
Convert 49710 to the base-5 number system
Given: 49710
Now, we have to convert the decimal system to base-5 system.
So, divide the given number by 5.
Step 1: Divide 497 by 5.
⇒ Quotient = 99 & Remainder = 2
Step 2: Divide 99 by 5.
⇒ Quotient = 19 & Remainder = 4
Step 3: Divide 19 by 5.
⇒ Quotient = 3 & Remainder = 4
Step 4: Divide 3 by 5.
⇒ Quotient = 0 & Remainder = 3 Hence, 49710 = 34425
19
497/5 = 99.4 99 is quotient
and remainder is 0.4*5 = 2
99/5 = 19.8 19 is quotient
and remainder is 0.8*5 = 4
19/5 = 3.8 3 is quotient
and remainder is 0.8*5 = 4
497 10 to base-5

20. Example:
Convert 38010 to the hexadecimal number system
Given: 38010
Now, we have to convert the decimal system to the hexadecimal number system.
So, divide the given number by 16.
Step 1: Divide 380 by 16.
⇒ Quotient = 23 & Remainder = 12 (12 can be represented as “C” in hexadecimal)
Step 2: Divide 23 by 16.
⇒ Quotient = 1 & Remainder = 7
Step 3: Divide 1 by 16.
⇒ Quotient = 0 & Remainder = 1
Hence, 38010 = 17C16.
20
16
0 - 1 1
7
C

21. Conversion from One Number System to Another
Number System
● To convert a number from one of the binary or octal or hexadecimal or
etc systems to one of the other systems, we first convert it into the
decimal system, and then we convert it to the required systems by using
the previously-mentioned processes.
21
Binary Octal
Hexadecimal Base-3
Decimal

22. Example: Convert 10101111002 to the
hexadecimal system.
● Step 1: Convert this binary number to the decimal number system as explained in
the previous process.
22

23. Example: Convert 10101111002 to the
hexadecimal system.
● Thus, 10101111002 = 70010
● Step 2: Convert the above number (which is in the decimal system), into the
required number system (hexadecimal).
● Here, we have to convert 70010 into the hexadecimal system using the above-
mentioned process.
23
● Thus, 70010 = 2BC16
● So 10101111002 = 70010 = 2BC16
16
0 - 2

24. Example: Convert 10101111002 to the
hexadecimal system.
24
Is there any shortcut to convert from binary to hexadecimal and
vice-versa? YES
By grouping 4 binary digits together from right to left and then
memorising the hexa-binary table for conversion. If you cannot
make groups of 4 in the left end, add leading zeroes.
Do the opposite to convert from hexadecimal to binary.
N.B. this shortcut can only be applied for conversion between binary and hexadecimal

25. Shortcut Example:
Convert 10101111002 to the hexadecimal system.
25
0010 1011 1100
12
C
B
2 11
2
Decima
l
Hexadecimal
in hexadecimal
Binary

26. Shortcut Example:
Convert 2BC16 to the binary system.
26
0010 1011 1100
12
11
2
C
B
2
Decima
l
Hexadecimal
in binary
Binary

27. Example: 2F16 + 2134 * 1210 = ?9
27
4710 3910 1210
+ *
46810
4710 +
51510
hexa
to
decimal
base 4
to
decimal
Do multiplication first, then addition.
as multiplication has greater precedence
than addition.
6329
decimal to base 9
Any mathematical operation can be done among numbers of
different bases by converting them to a common base ( mostly the
decimal number system )

28. Can you create a new number
system?
28

29. 29