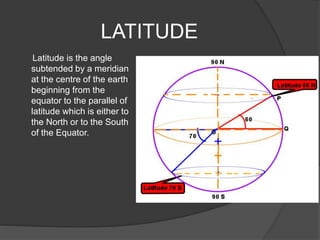
The document discusses latitude and longitude, which are used to locate places on Earth. Latitude is measured in degrees north and south of the equator, while longitude is measured in degrees east and west of the Prime Meridian in Greenwich, England. The document provides details on calculating distances between locations using their latitudes and longitudes, either along meridians of longitude or along the equator. It also discusses finding the shortest distance between two points, which follows a great circle route passing through the North and South Poles.

2. LATITUDE AND
LONGITUDE
 The coordinate system that we use to
locate places on Earth is the terrestrial
system. The coordinates in the
terrestrial system are Latitude and
Longitude.
e.g:
Kuala Lumpur ( 3 8’ N , 10142’ E )

5. LONGITUDE
 Longitude, denoted symbolically by the
Greek letter Lambda, is divided in
meridians (not parallel to each other,
they converge at the poles), which are
measured in degrees East or West of
the Prime Meridian, also known as
Greenwich Meridian The Prime Meridian
serves as a starting point for the
measurement of degrees in either East
or West directions. It marks longitude 0°.

6. LONGITUDE

7. LONGITUDE
The Prime Meridian is the
meridian (line of longitude) at
which the longitude is defined
to be 0°.
The Prime Meridian and its
opposite the 180th meridian (at
180° longitude), which the
International Date Line
generally follows, form a great
circle that divides the Earth
into the Eastern and Western
Hemispheres.

8. LONGITUDE

9. LONGITUDE
 Another meridian of great importance is
the Dateline Merdian, which marks
longitude 180° (either E or W). This
meridian is the exact oposite of the
Prime Meridian on the globe.

10. LONGITUDE
Meridian
- is one half of a great circle joining the
North and South Poles.
Longitude of a meridian
- is determined by the angle between its
plane and the plane for GM , either to
the east or to the west of the GM.

11. LONGITUDE
150 E

12. LONGITUDE
Meridians that are opposite to
each other and form a great
circle, have longitudes
x E and ( 180 – x) W
or x W and (180-x) E
- Great circle is a circle with
centre at the centre of the
Earth.

13. Longitude

14. The Difference between Two
Longitudes
 If longitudes X and Y are on the same
side of the GM, then the difference
between X and Y is ( X – Y).
 If the longitudes X and Y are on the
different sides of the GM , then the
difference between X and Y is ( X + Y )

15. Longitude

16. LATITUDE

17. LATITUDE
 Parallels of latitude are circles on the surface of
the Earth, parallel to the equator and labeled
according to their angular distance from the
equator.
Parallel of
latitudes is NOT
a great circle !

18. LATITUDE
Latitude is the angle
subtended by a meridian
at the centre of the earth
beginning from the
equator to the parallel of
latitude which is either to
the North or to the South
of the Equator.

19. LATITUDE

20. LATITUDE
DIFFERENCE BETWEEN TWO
LATITUDES
- If latitudes X and Y are on the same side of
the Equator, then the difference between X
and Y is ( X – Y).
If the latitudes X and Y are on the different
sides of the Equator , then the difference
between X and Y is ( X + Y )

21. LATITUDE
Calculate the difference
between the latitudes
below
i. Latitudes 70N and
64N
ii. Latitudes 64N and
55S

22. LOCATION OF A PLACE
The location of a
place is determined
by its latitude and
longitude. Based on
the diagram state
the location s of A ,
B ,C , D and E

23. LOCATION OF A PLACE

24. DISTANCE ON THE SURFACE
OF THE EARTH.
 The distance between two places on the
surface of the Earth is measured in
nautical miles.
 1 is equal to 60 nautical miles.
 Any two points on a sphere is always
connected by a circular path.
 The shortest distance between two
points is the distance taken along the
great circle.

25. DISTANCE BETWEEN TWO
POINTS ALONG THE
MERIDIAN
Distance of two points on the
surface of the Earth measured
along the meridian ( same
longitude, different latitude) is
given by
= ( the difference in latitude X 60’ )
= (   60’ )

26. DISTANCE BETWEEN TWO
POINTS ALONG THE
MERIDIAN
Given that P(60N,30 W)
and Q ( 40 S , 30W) ,
find the distance of PQ
measured along the
meridian.
Answer:
Distance = ( 60 + 40 )  60’
= 100 x 60’
= 6000 nautical miles.

27. DISTANCE BETWEEN TWO
POINTS ALONG THE
MERIDIAN
In the diagram , A ( 45N ,
30E) and B are two points
on the surface of the earth.
Given that the distance
between A and B is 4800
nm measured along the
longitude 30E . Find the
location of B

28. DISTANCE ALONG THE
EQUATOR
The distance between points P
and Q on the Equator ( same
latitude, different longitude) is
equivalent to the angle at the
centre of the earth POQ, in
minutes.
= (difference in longitude ) x 60’

29. DISTANCE ALONG THE
EQUATOR
 Example:
Given that P( 0, 124W) , Q (0, 72W)
and R( 0, 27 E ). Calculate the
distance between
i. P and Q
ii. Q and R

31. DISTANCE ALONG THE
EQUATOR
 Example;
Given that P(0, 160W) and the
distance between P and Q measured
along the Equator is 5400 n.m. Find all
the possible locations of Q.

33. Relation Between Radius of the
Earth and Radius of a Parallel
of Latitude
OP = OQ = R
AQ is parallel to OP
POQ =  OQA ( alternate
angle of two parallel lines)
By trigonometric ratio ,
Cos  =
Therefore, r = R Cos 
r
R
r

34. Relation between the Lengths
of Arcs on the Equator and
Parallels of Latitude
-Let r be the radius of the parallel of
latitude and R be the radius of the
Equator.
-Then , the circumference of the parallel
latitude is 2r and the circumference of
the Equator is 2R

35. Relation between lengths of Arc
on the Equator and parallels of
latitude

36. Distance along the parallel of
latitude
Distance of PQ = MN (Cos )
= MON  60  Cos 
= Diff. in long of PQ  60 Cos(lat of PQ)
eg: Find the distance between
P( 60N, 35W) and
Q( 60N, 45 E).

37.  Find the distance between P( 60N,
35W) and Q( 60N, 45 E).
//
Dist. of PQ = (diff. in longitude)  60’ Cos 
= (35 + 45 )  60  Cos 60
= 2400’
 Distance of PQ = 2400 n.m

38. SHORTEST DISTANCE
BETWEEN TWO POINTS
 The shortest distance between two
points on the surface of the Earth is the
arc on the great circle that passes
through the two points.
 The Equator and all circles passing
through the North and South Poles are
great circles.

39. SHORTEST DISTANCE
a. Along the meridian ( same
longitude )
b. Along the Equator

40. SHORTEST DISTANCE
Distance of two points that passing
through the North/South Poles
* P and Q are on the same great
circle
*The difference in longitudes = 180
•The shortest distance of PQ
= ( POQ =  ) x 60’
= ( 180 - lat P – lat Q) 60’

41. Shortest Distance
 Calculate the shortest distance between
P ( 48N, 45E) and Q( 53N, 135W).
= 180
PQ ( shortest distance through North pole)
= (180 – 48 – 53) x 60’
= 4740’
= 4740 n.m