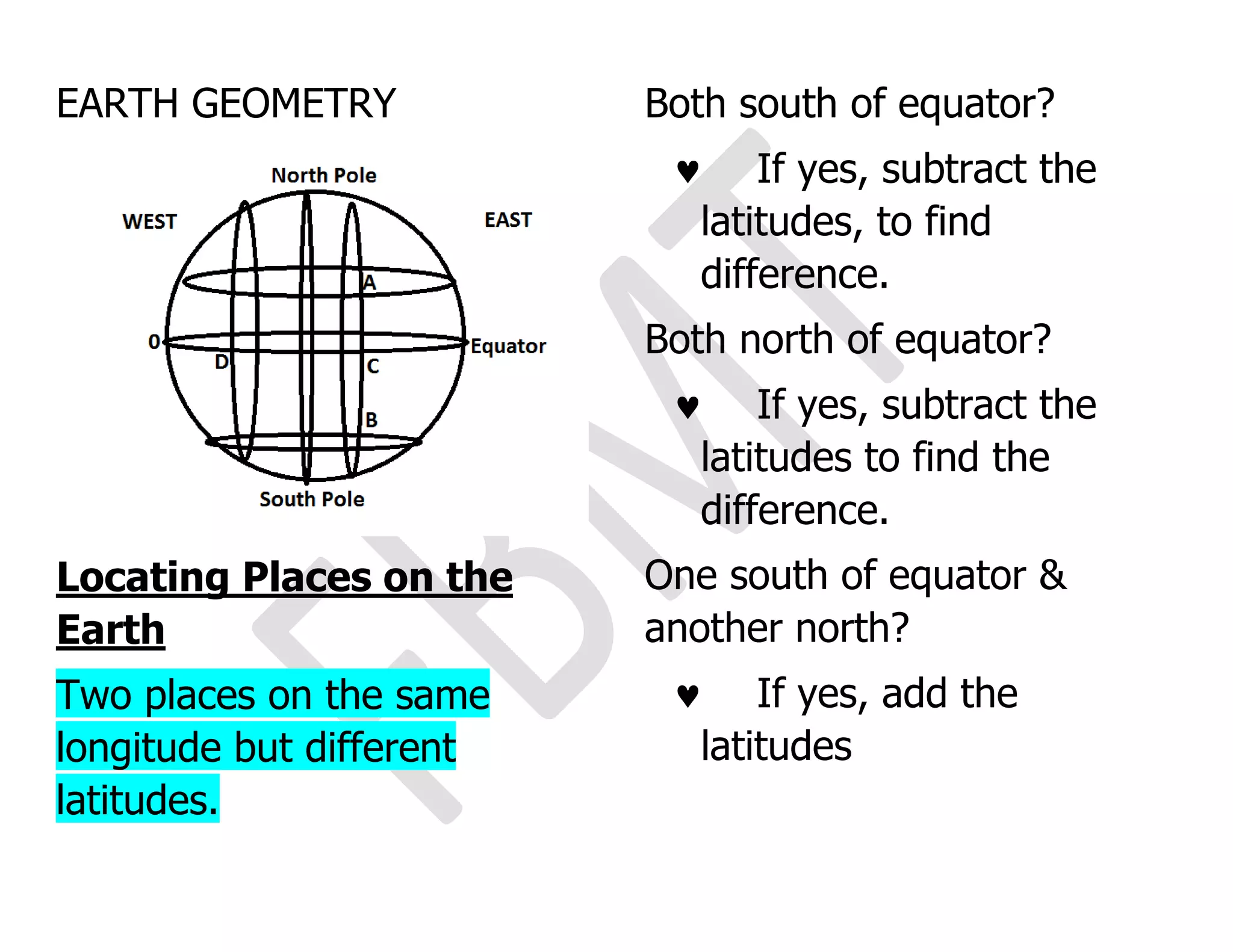
This document discusses how to locate places on Earth based on their latitude and longitude. It provides instructions for calculating the difference or sum of latitudes and longitudes depending on whether locations are north or south of the equator, or east or west of Greenwich. It also explains how to calculate the distance along parallels of latitude or along the Earth's surface between two locations given their latitude and difference in longitude.

1. EARTH GEOMETRY
Locating Places on the
Earth
Two places on the same
longitude but different
latitudes.
Both south of equator?
 If yes, subtract the
latitudes, to find
difference.
Both north of equator?
 If yes, subtract the
latitudes to find the
difference.
One south of equator &
another north?
 If yes, add the
latitudes

2. Two places on the same
latitude but different
longitudes.
Both east of Greenwich?
 If yes, subtract
longitudes
Both west of Greenwich?
 If yes, subtract
longitudes
One east & another west?
 If yes, add longitudes
Distance Along Places
The circle of latitude
∅° 𝑁 𝑜𝑟 ∅° 𝑆 has radius 𝑟 =
𝑅𝑐𝑜𝑠∅, where R=radius of
the Earth.
Arc length=
2𝜋𝑟𝜃
360

3. Examples.
1.Given that the radius of the
earth is 6400km, find
(i)The length of the parallel
latitude 30°𝑁
(ii)The shortest distance
along the surface of the
earth from town Q
(30°𝑁,10°𝐸)to town P
(30°𝑁,50°𝑊
Solution
(i)
Given that R=6400km
∅ = 30° 𝑁, ∅ = 30°
Length=2𝜋𝑟
r=Rcos∅
=2×
22
7
× 6400 × 𝑐𝑜𝑠30
=34,839km
(ii)
2𝜋𝑟𝜃
360
=
2×
22
7
×6400×𝑐𝑜𝑠30×60
360
=
5806𝑘𝑚
𝜃 = 10 + 50 = 60°
r=Rcos∅