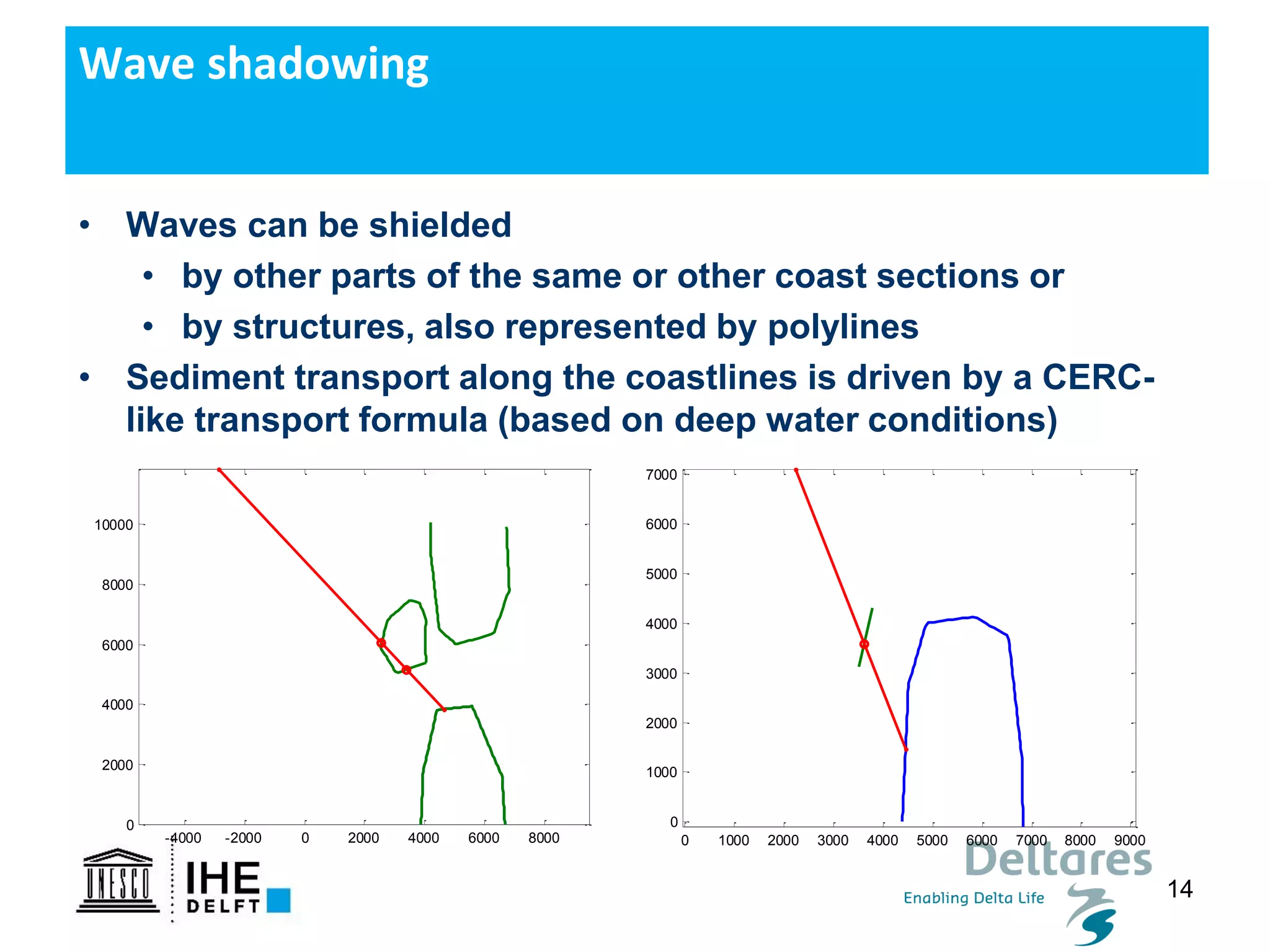
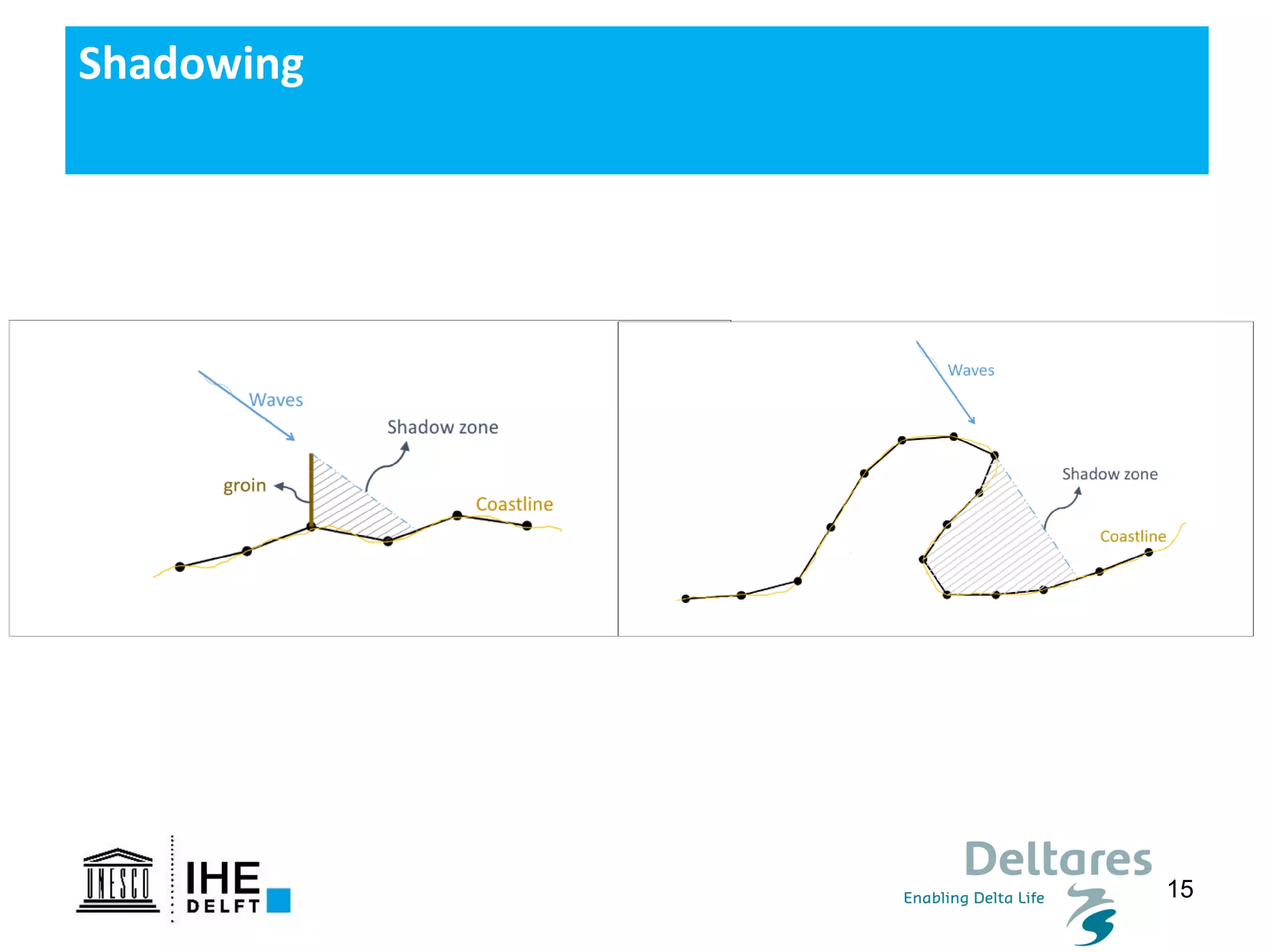
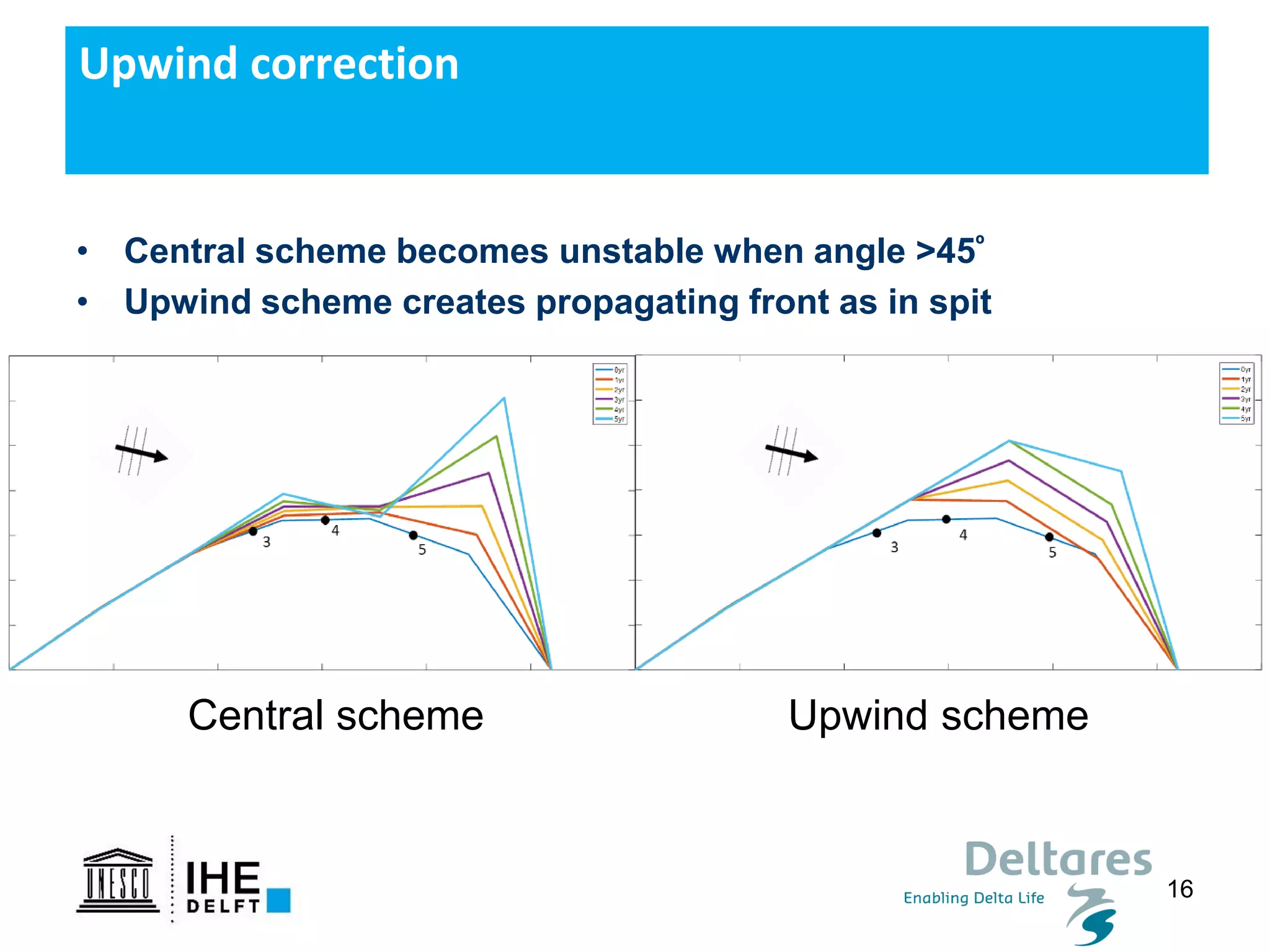
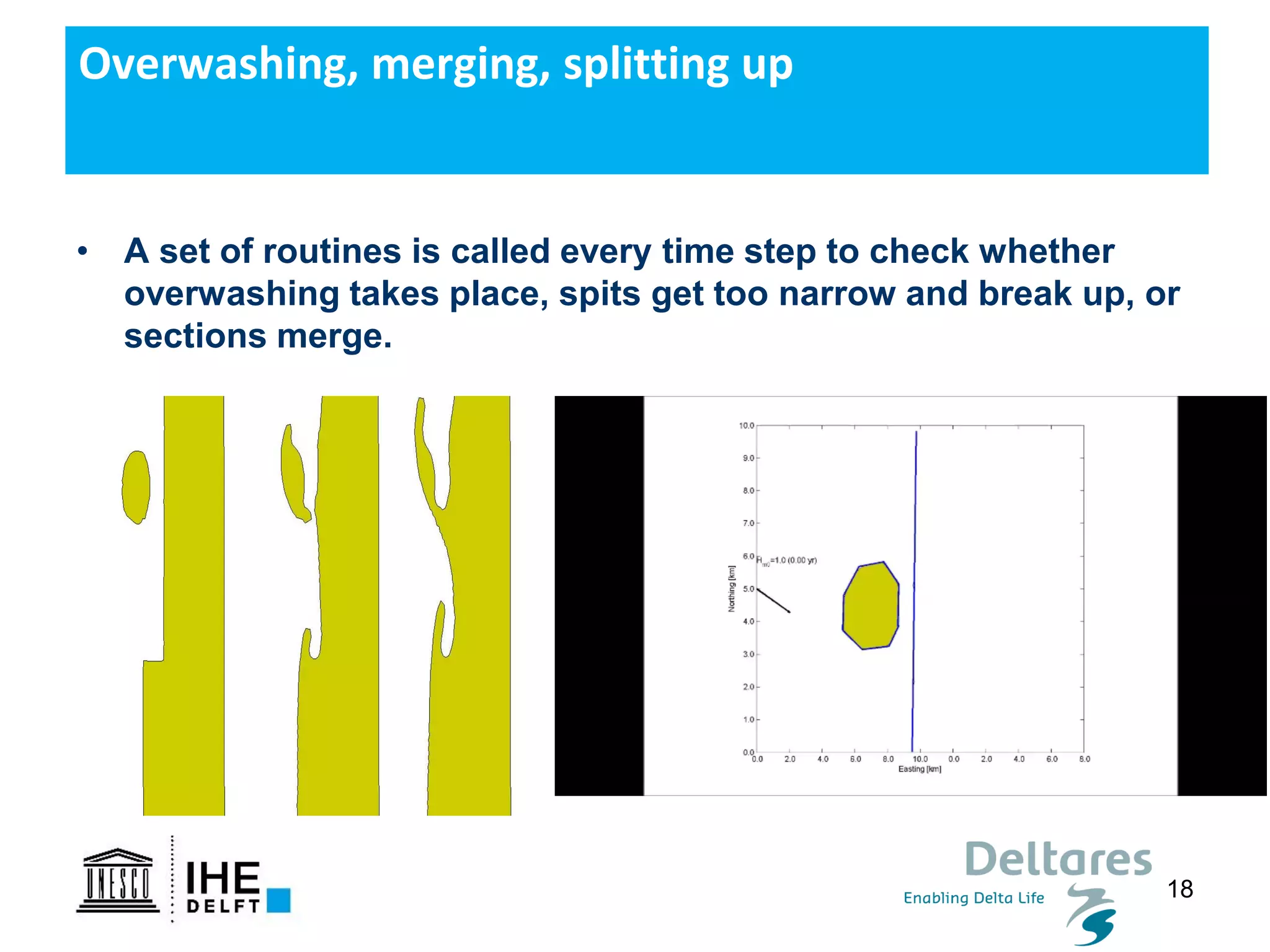
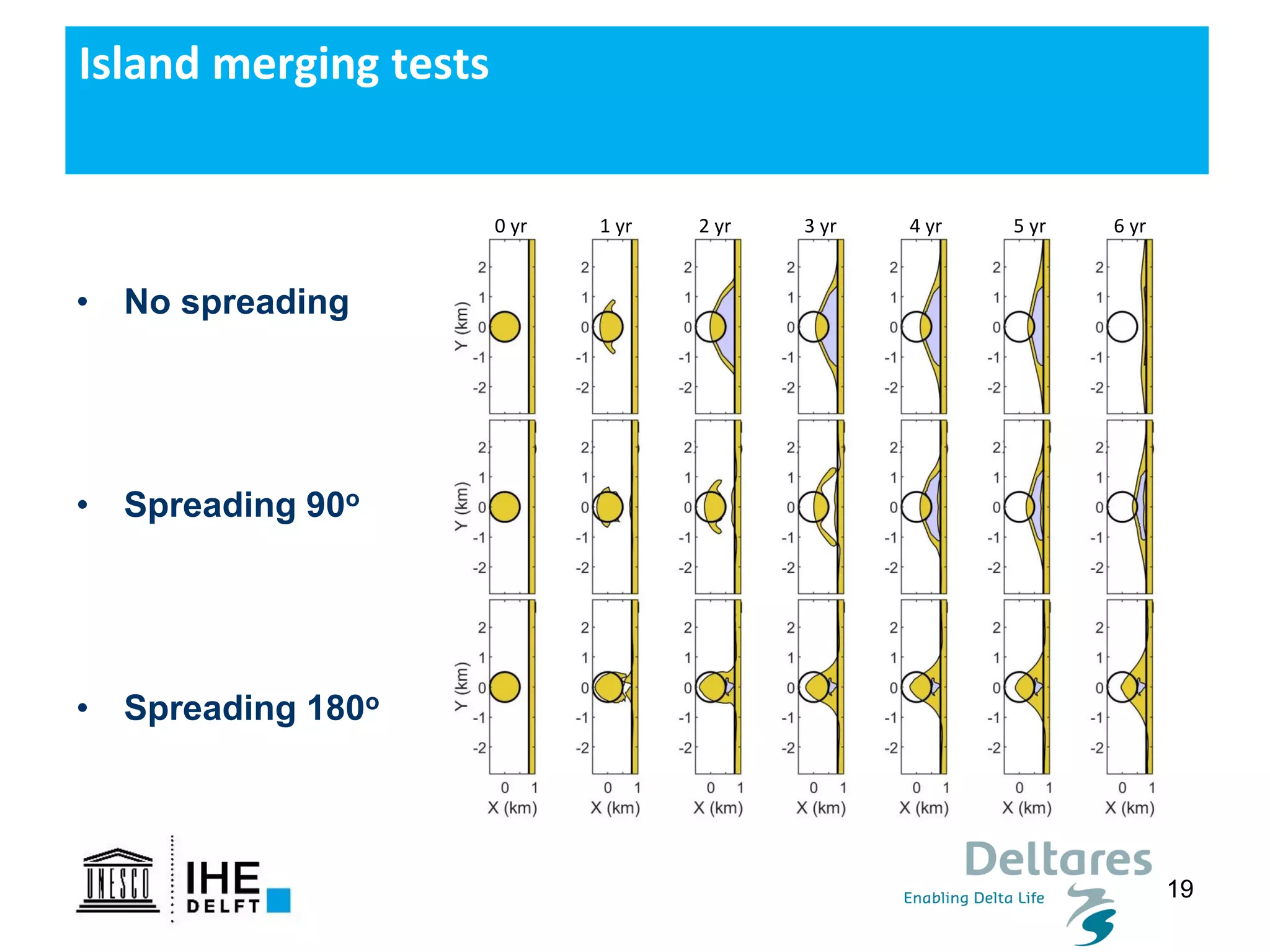
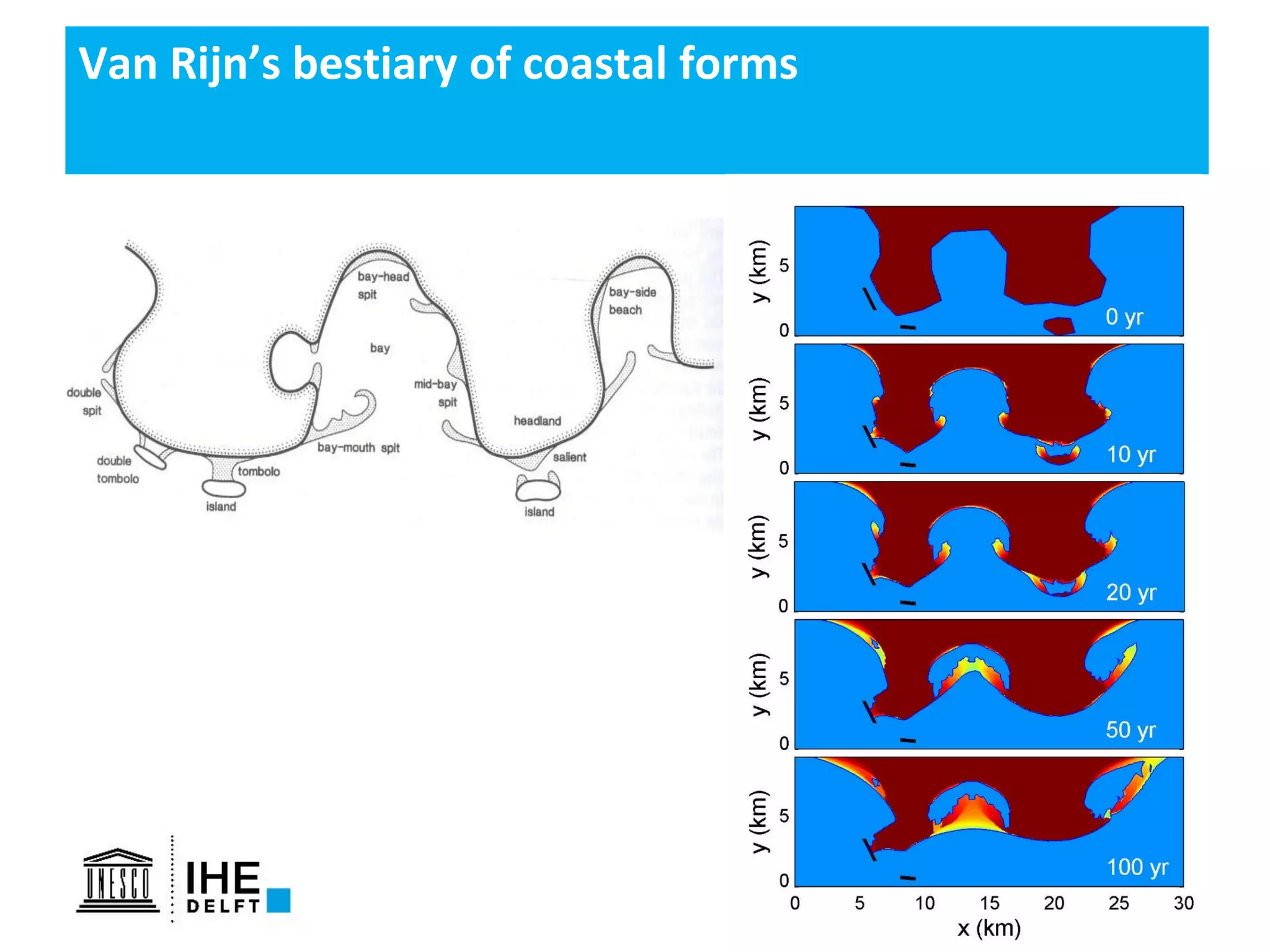
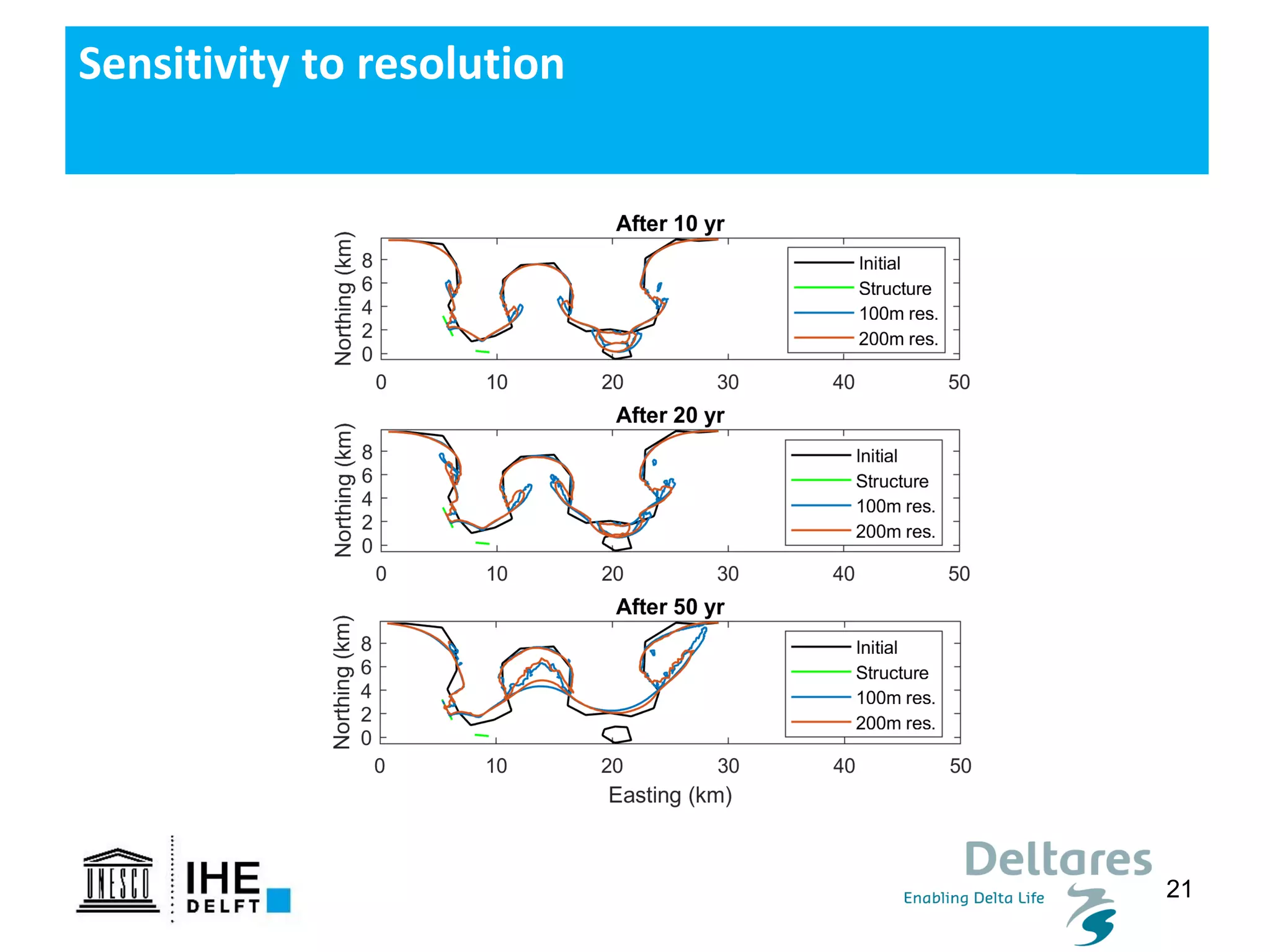
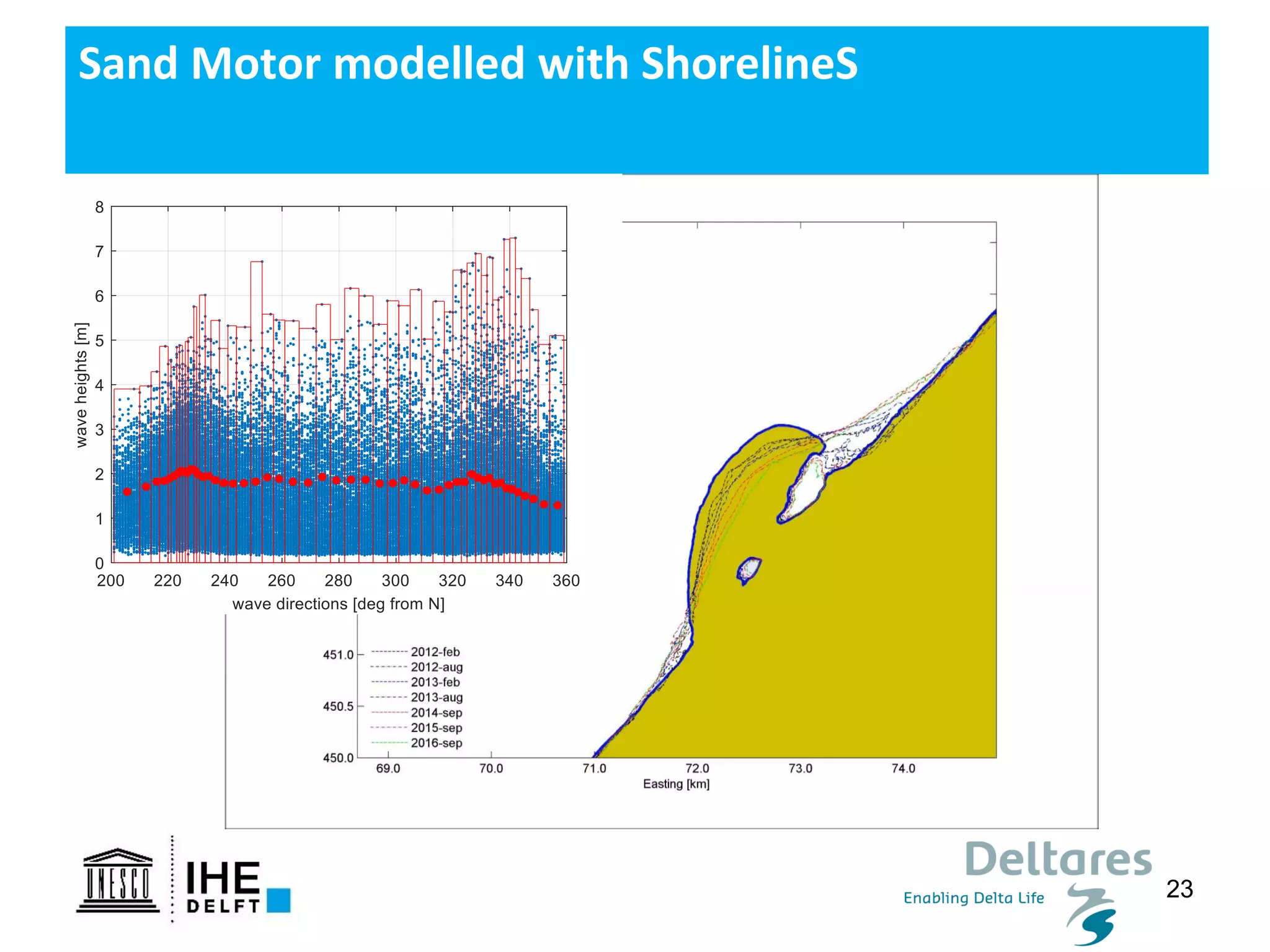
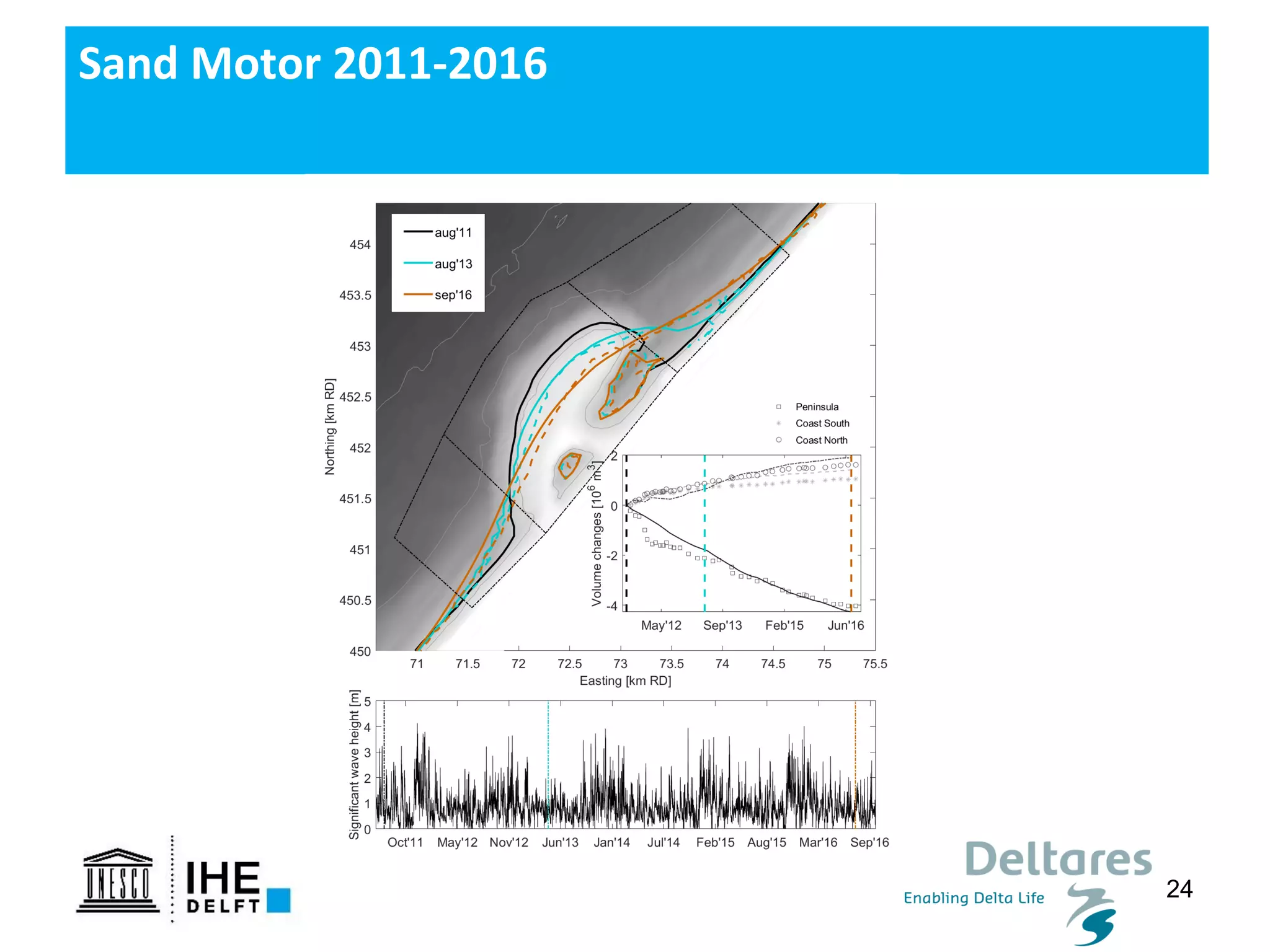
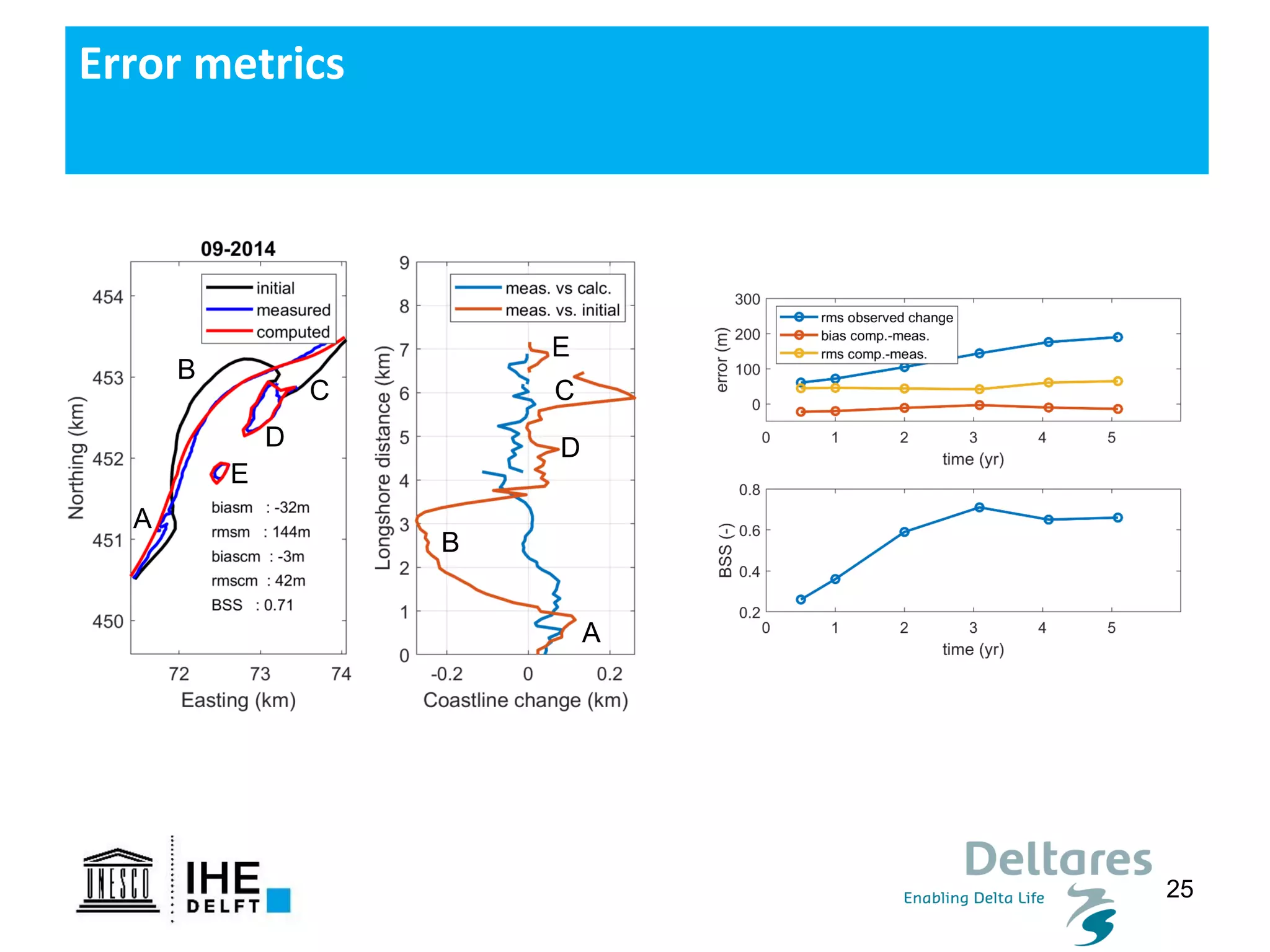
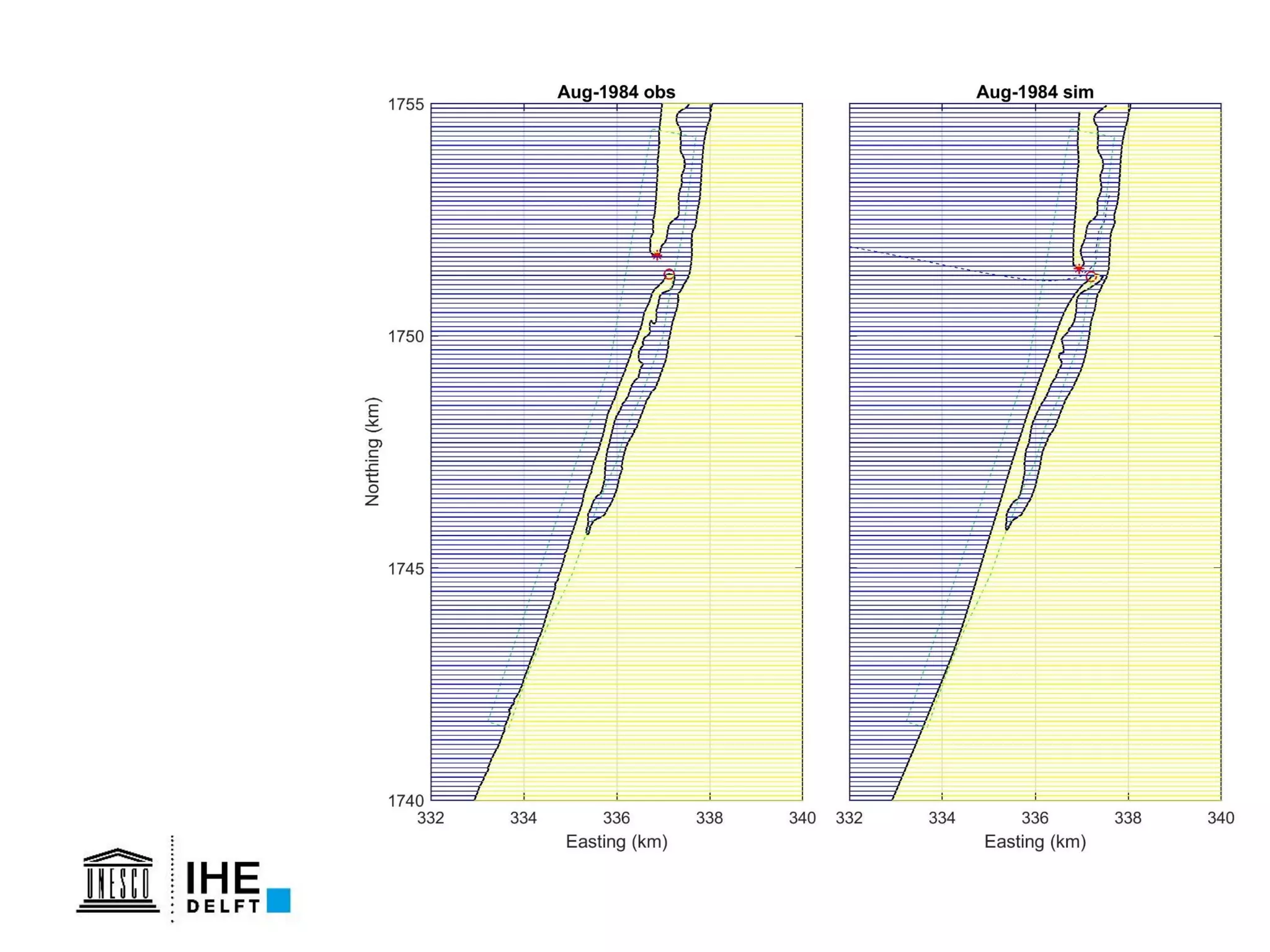
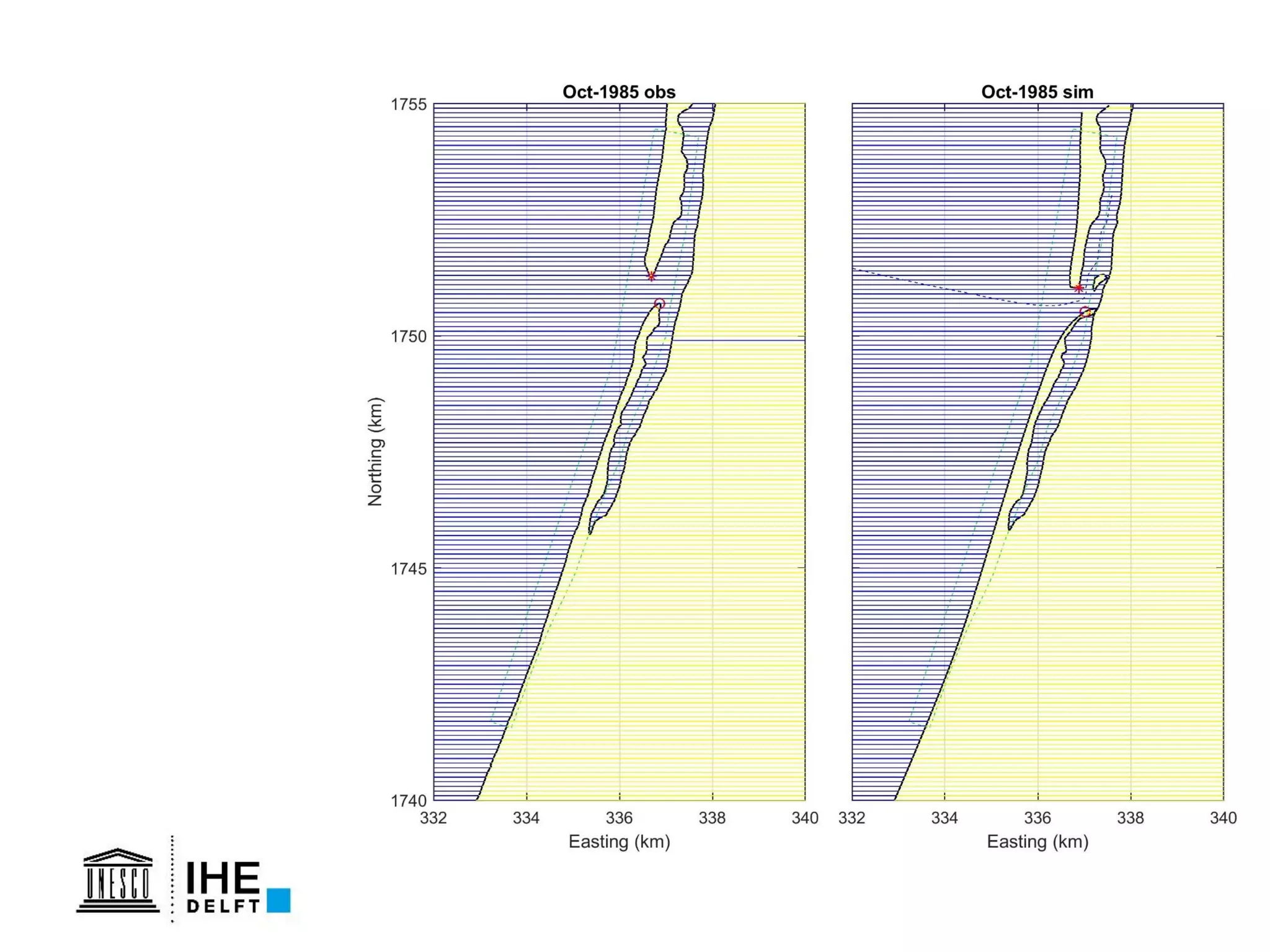
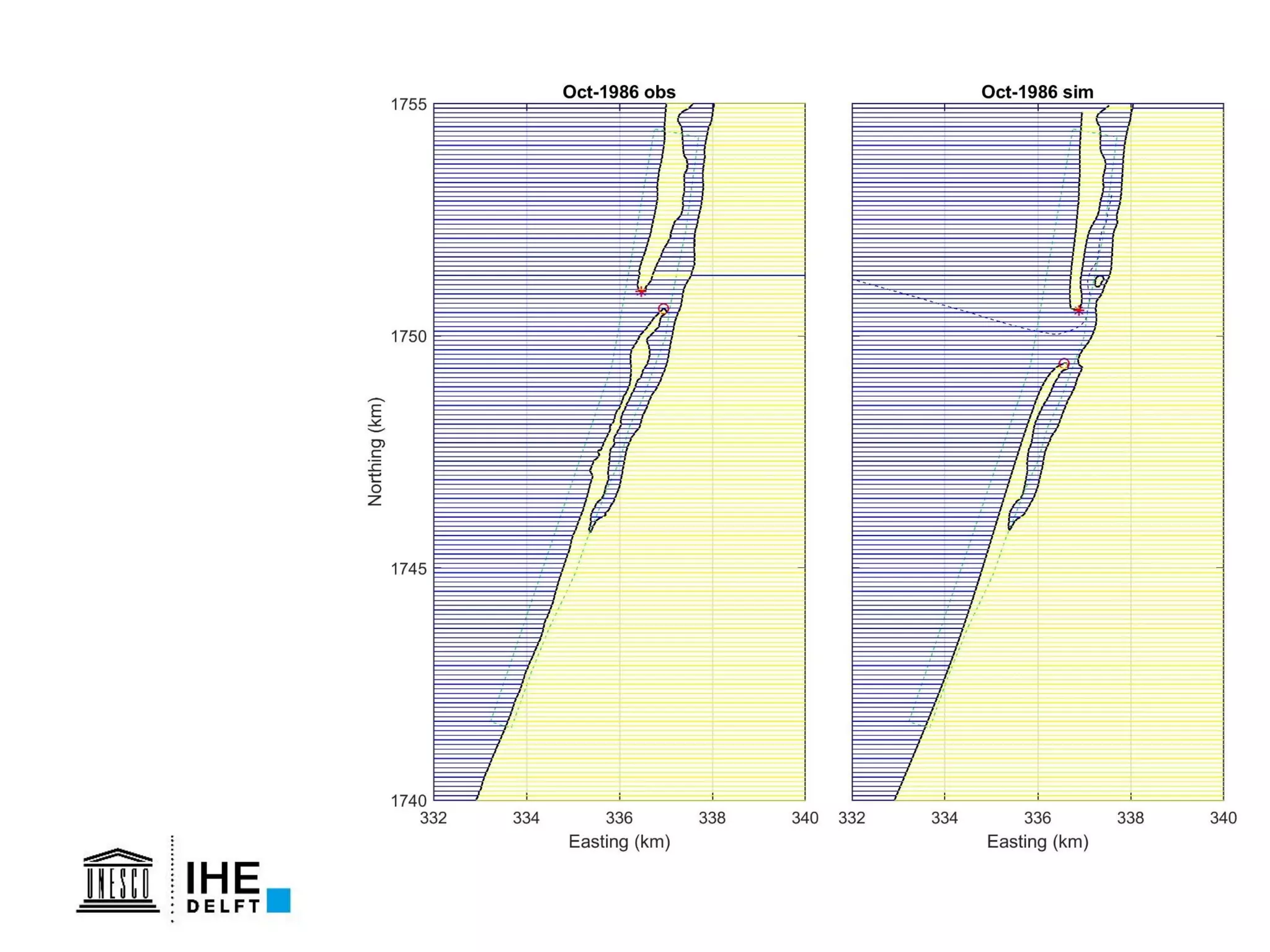
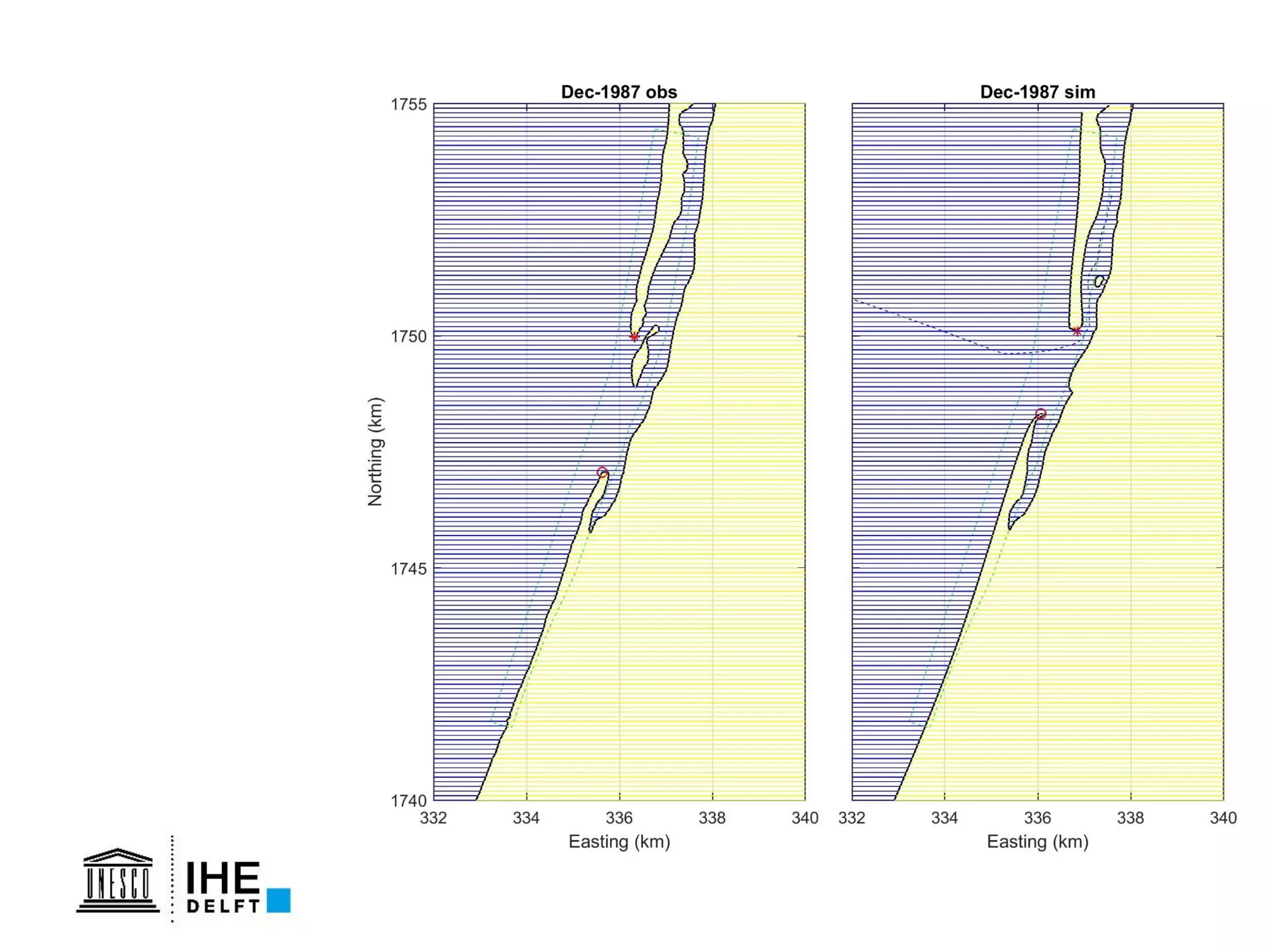
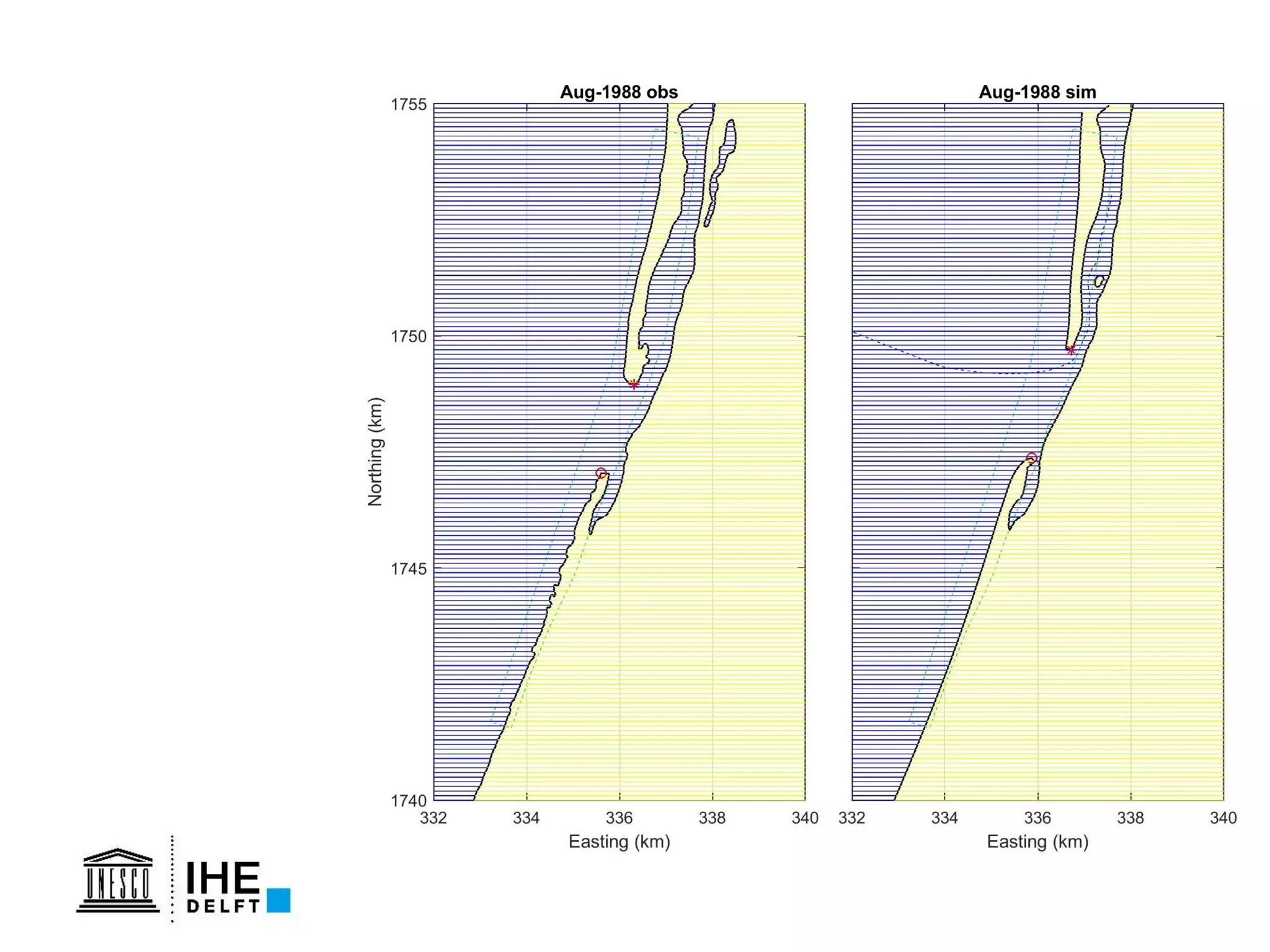
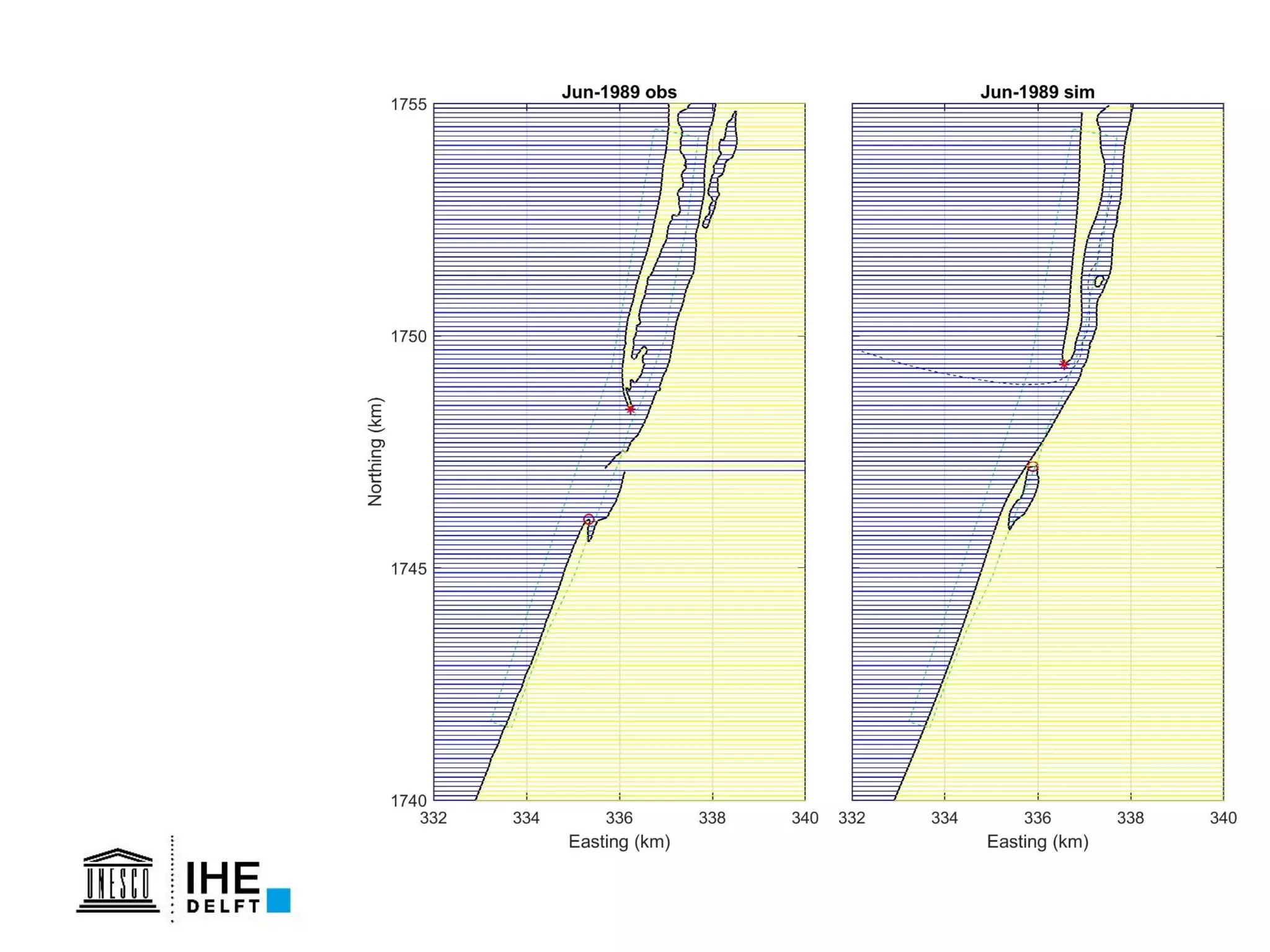
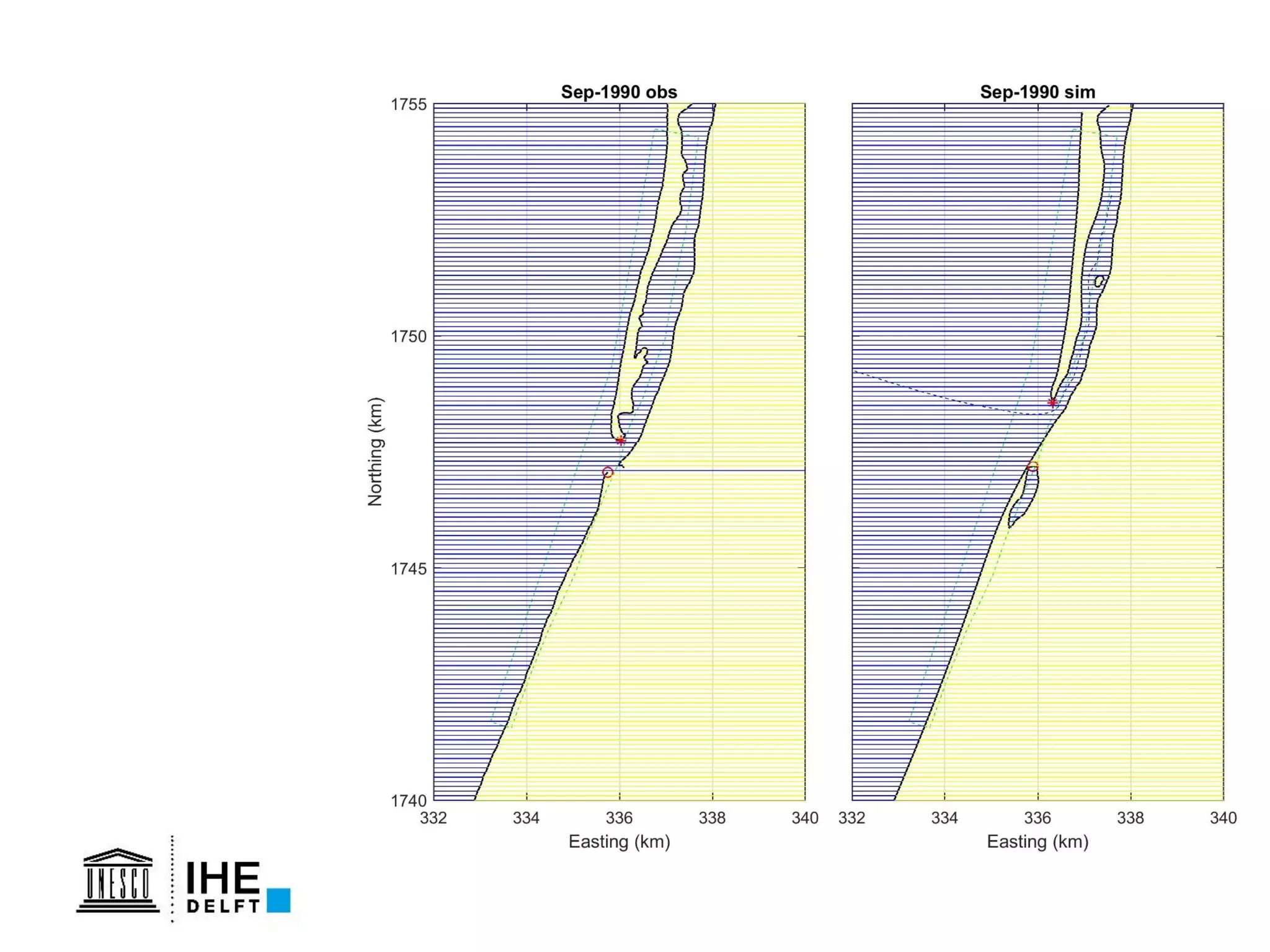
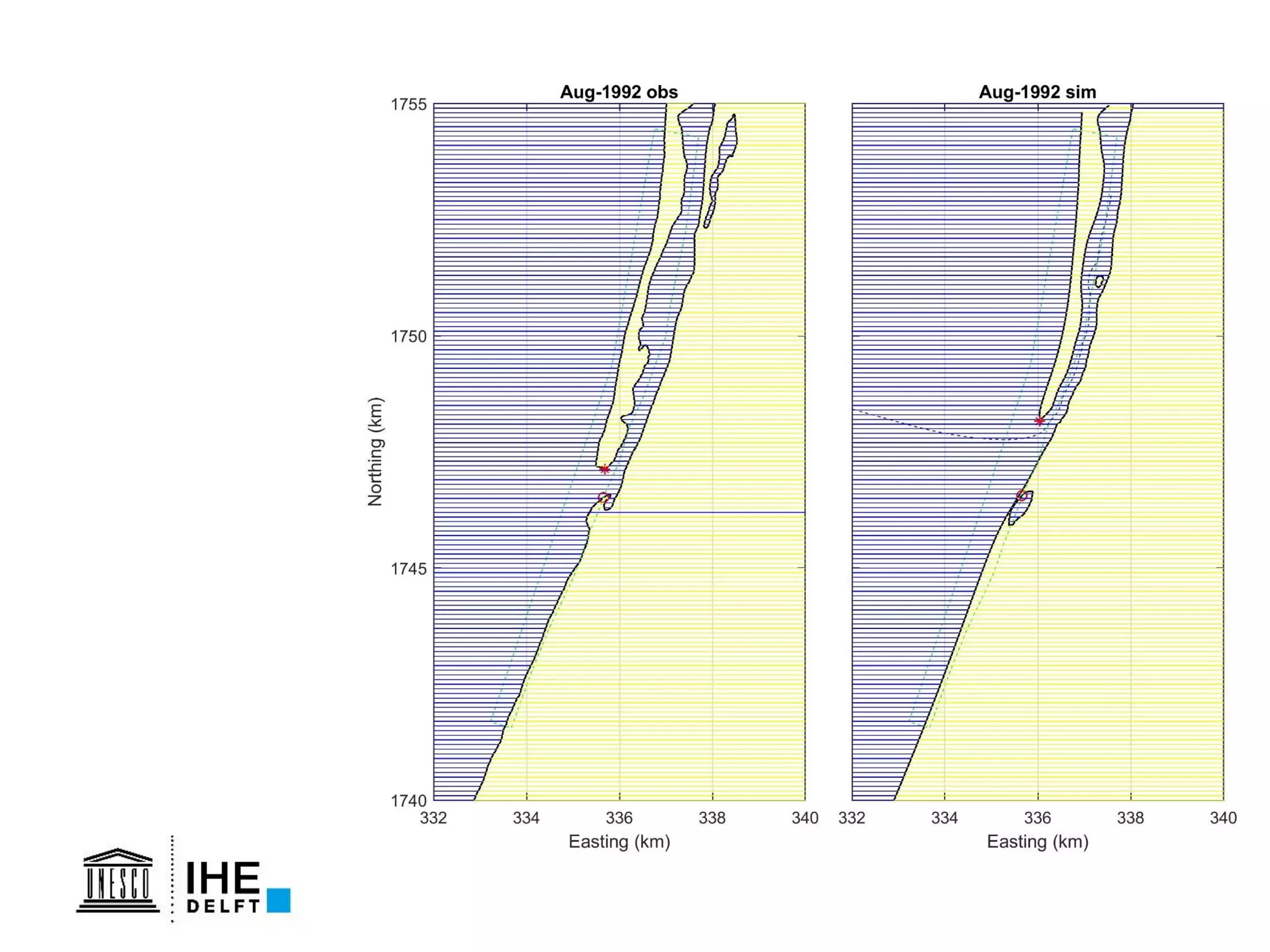
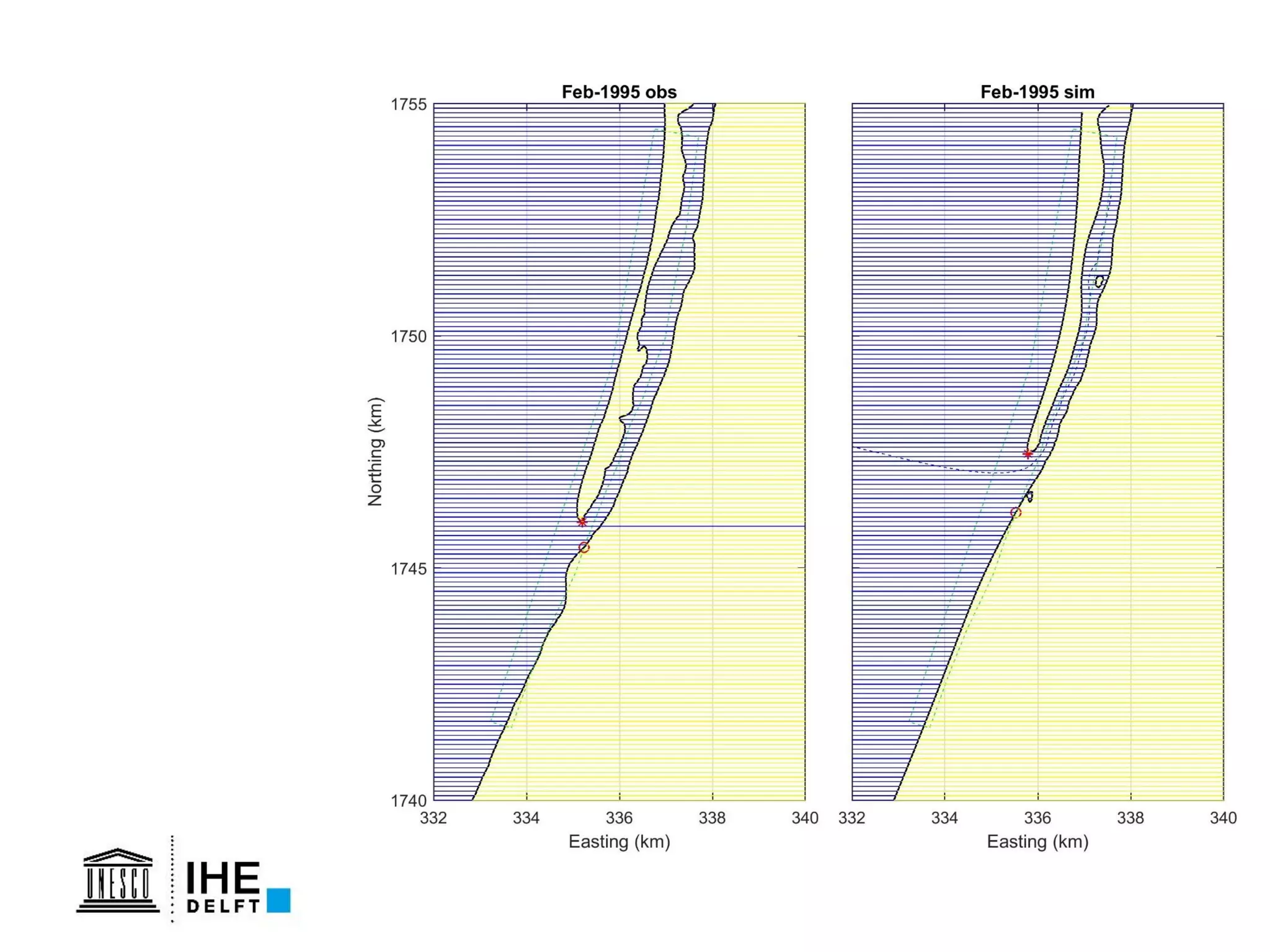
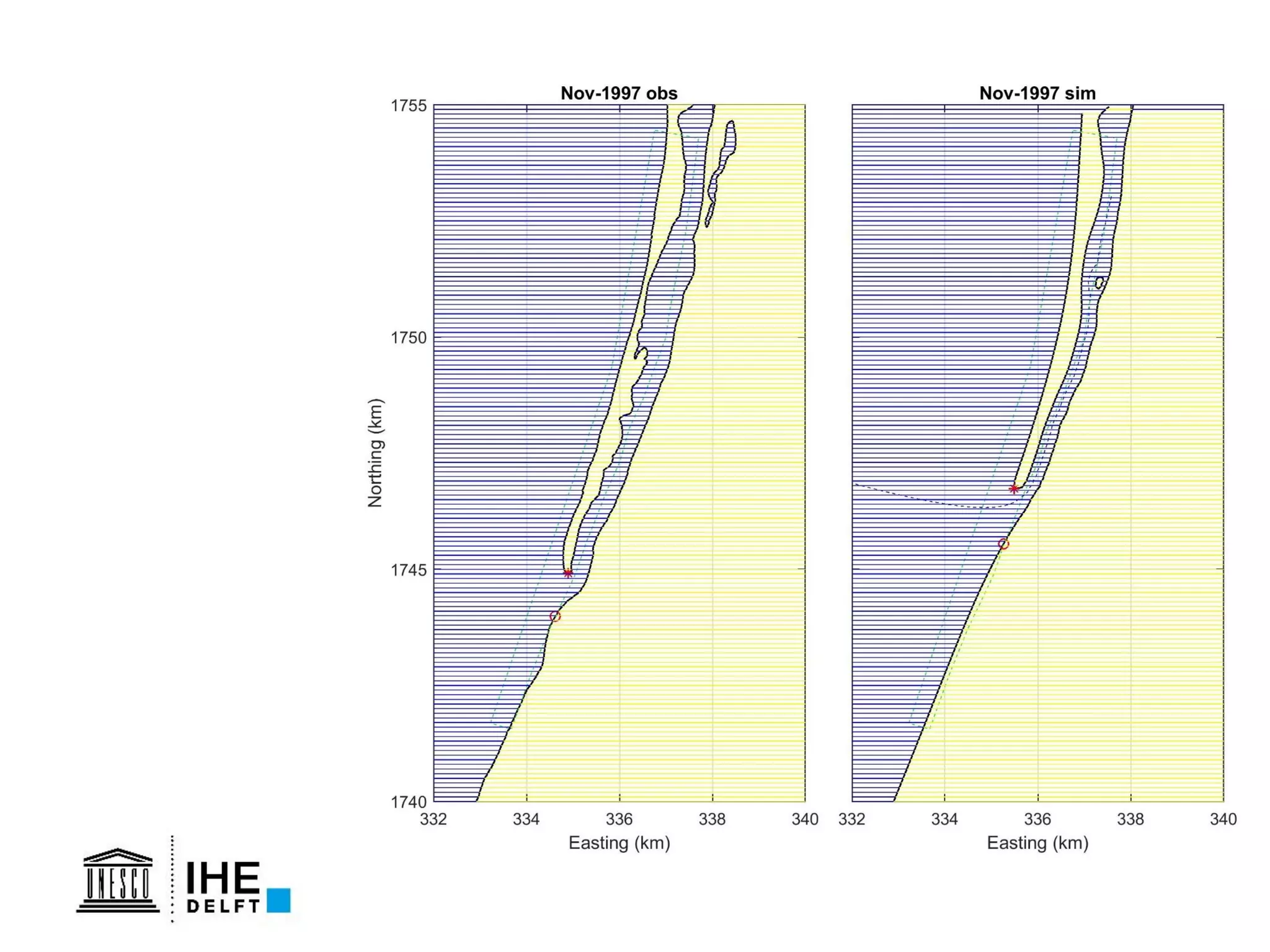
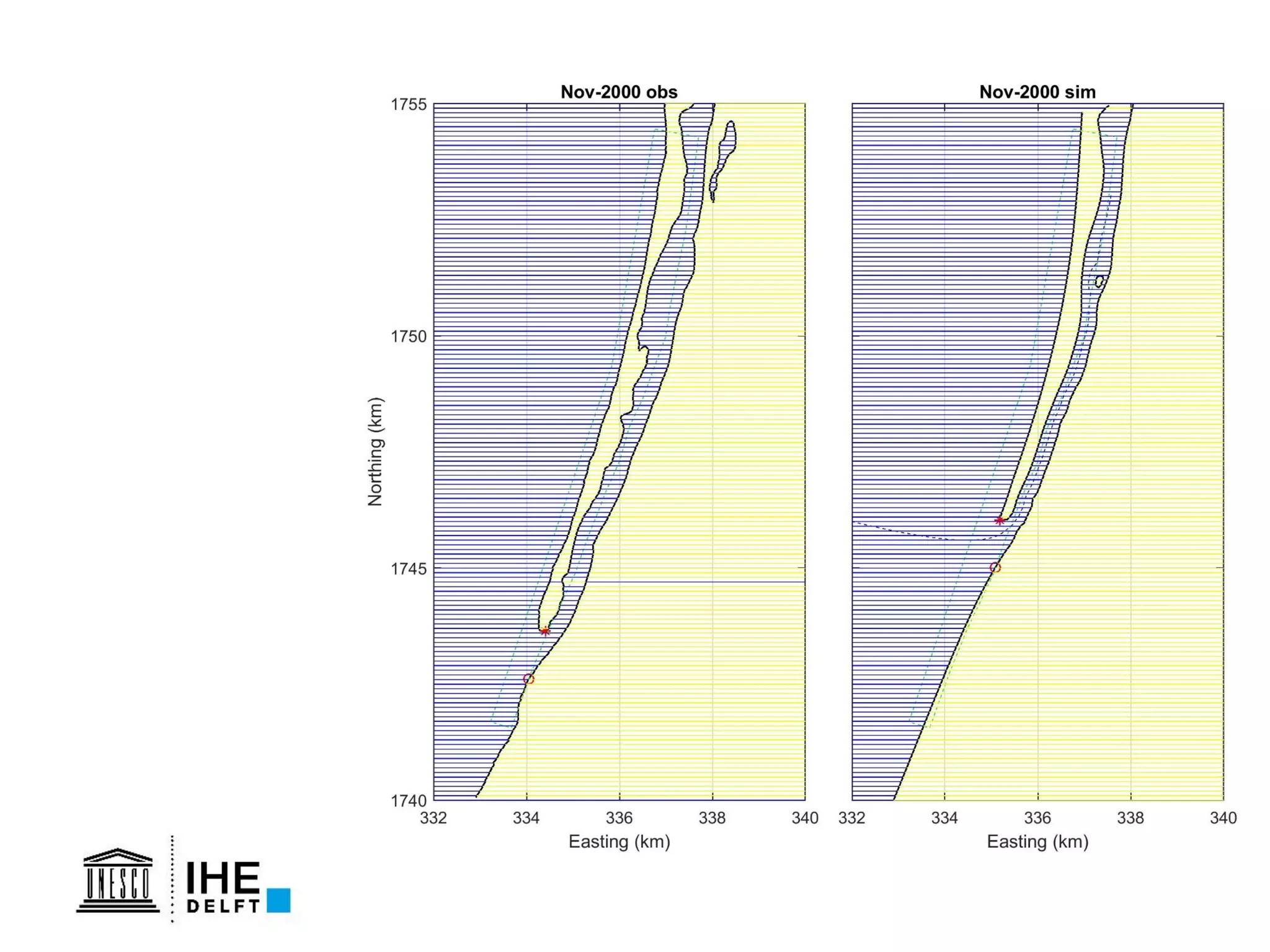
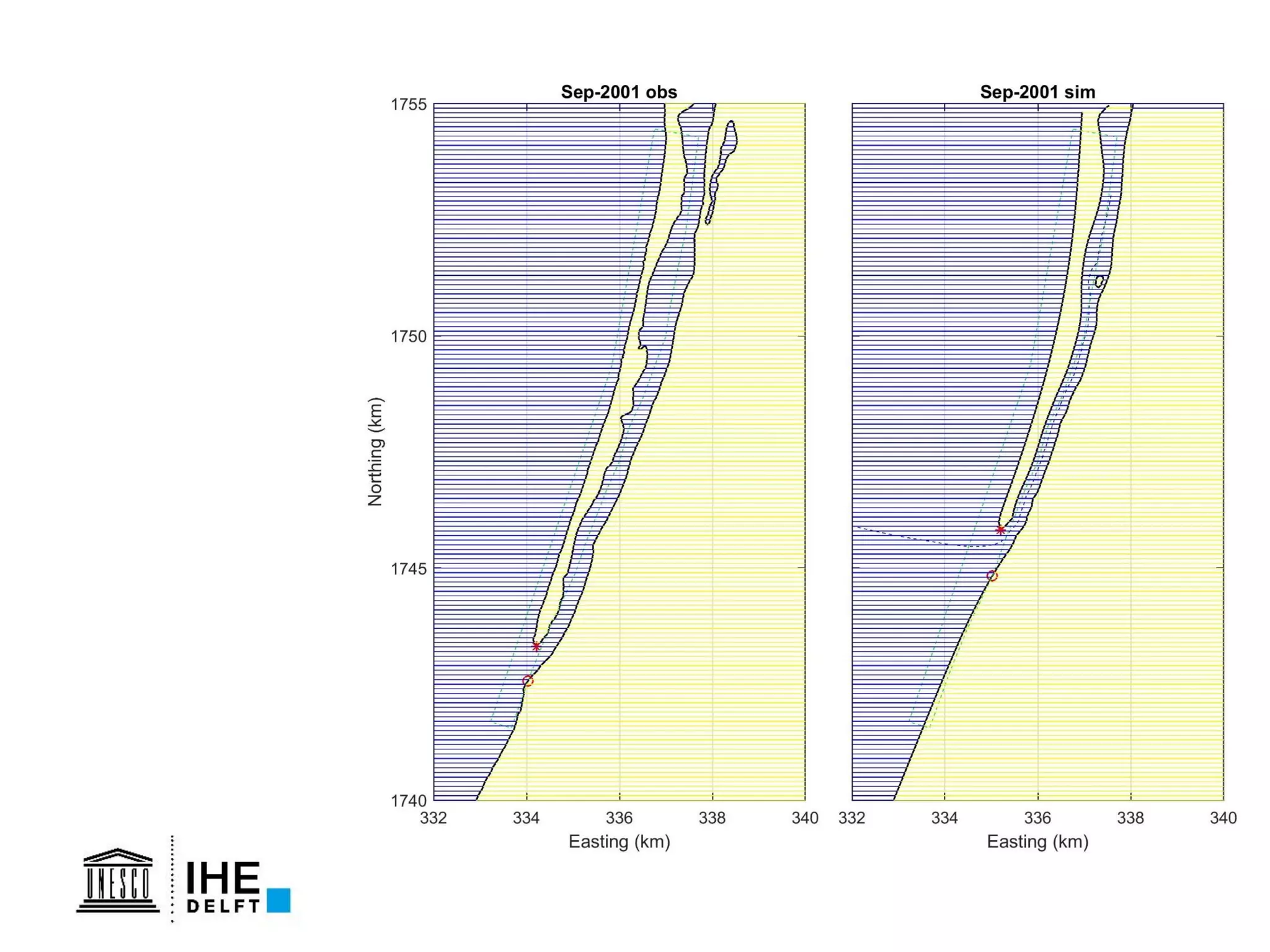
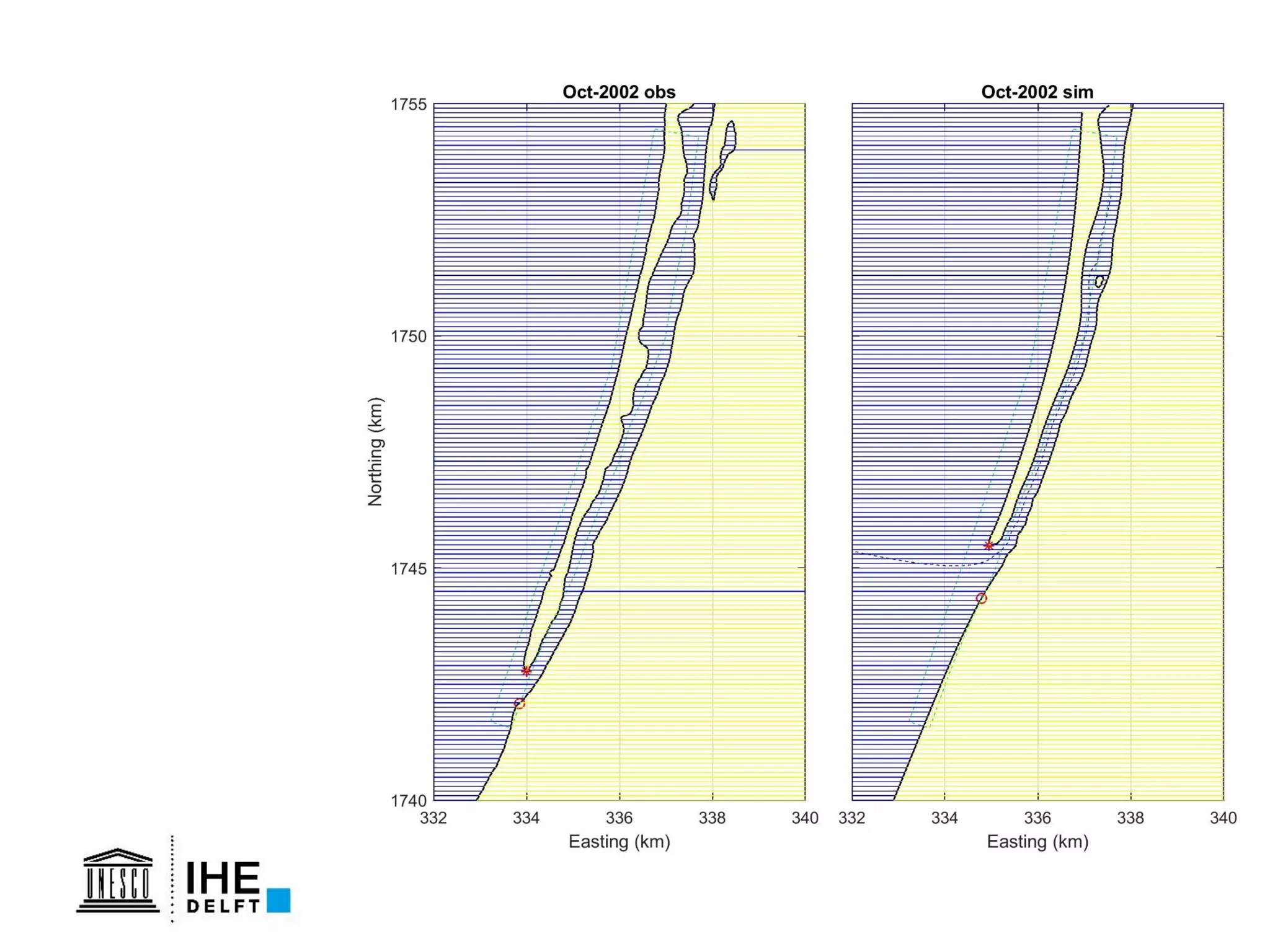
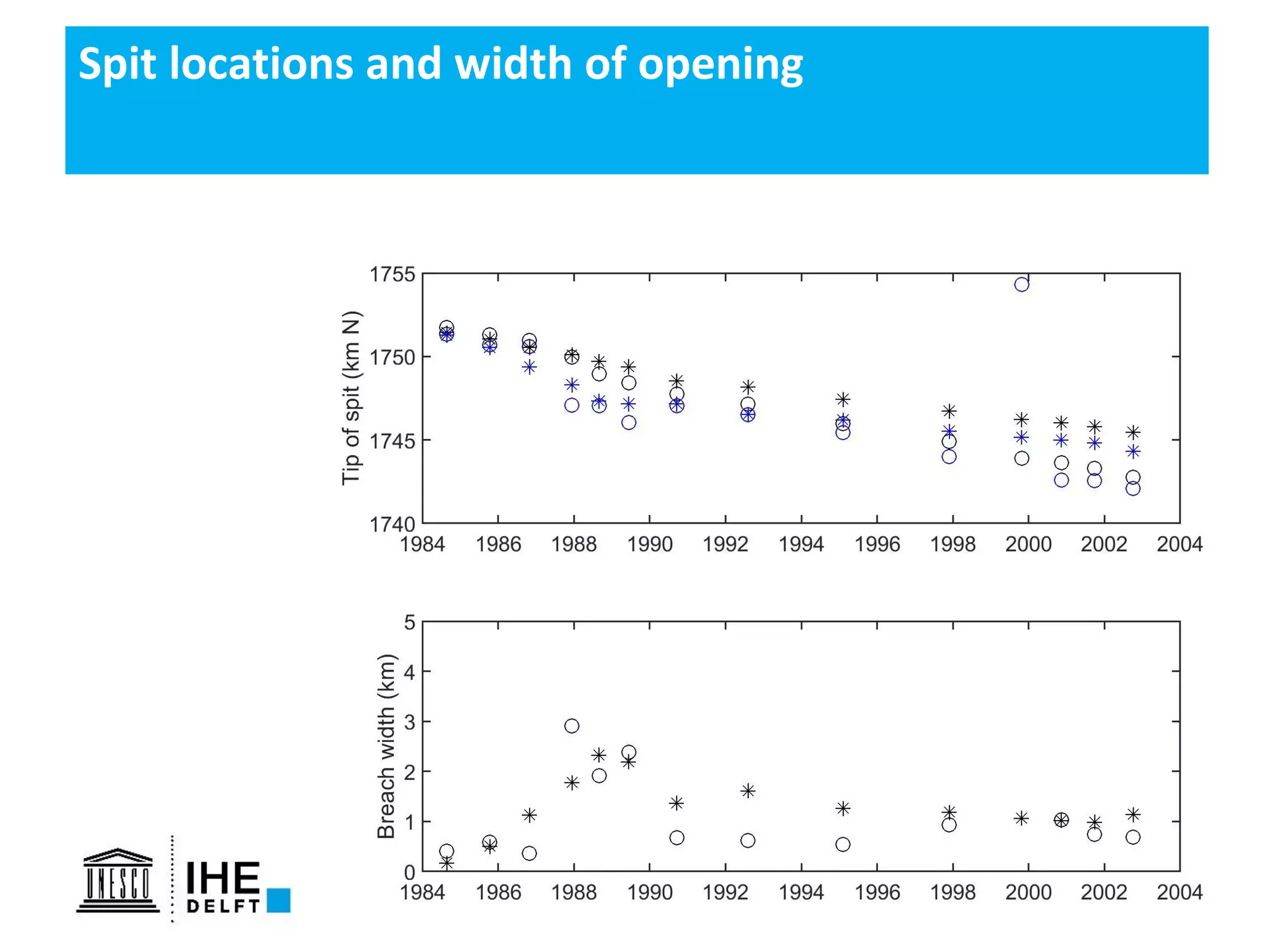
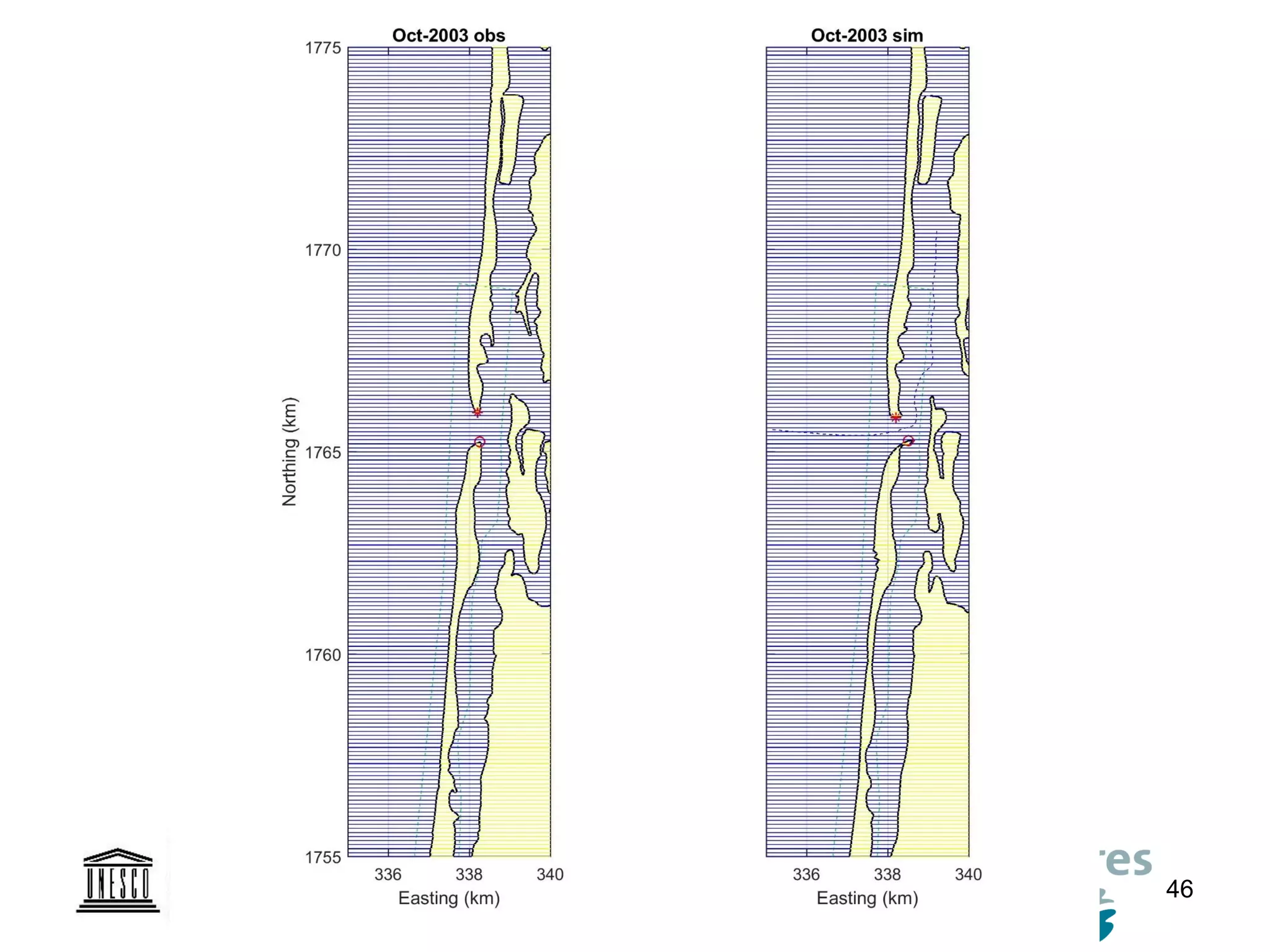
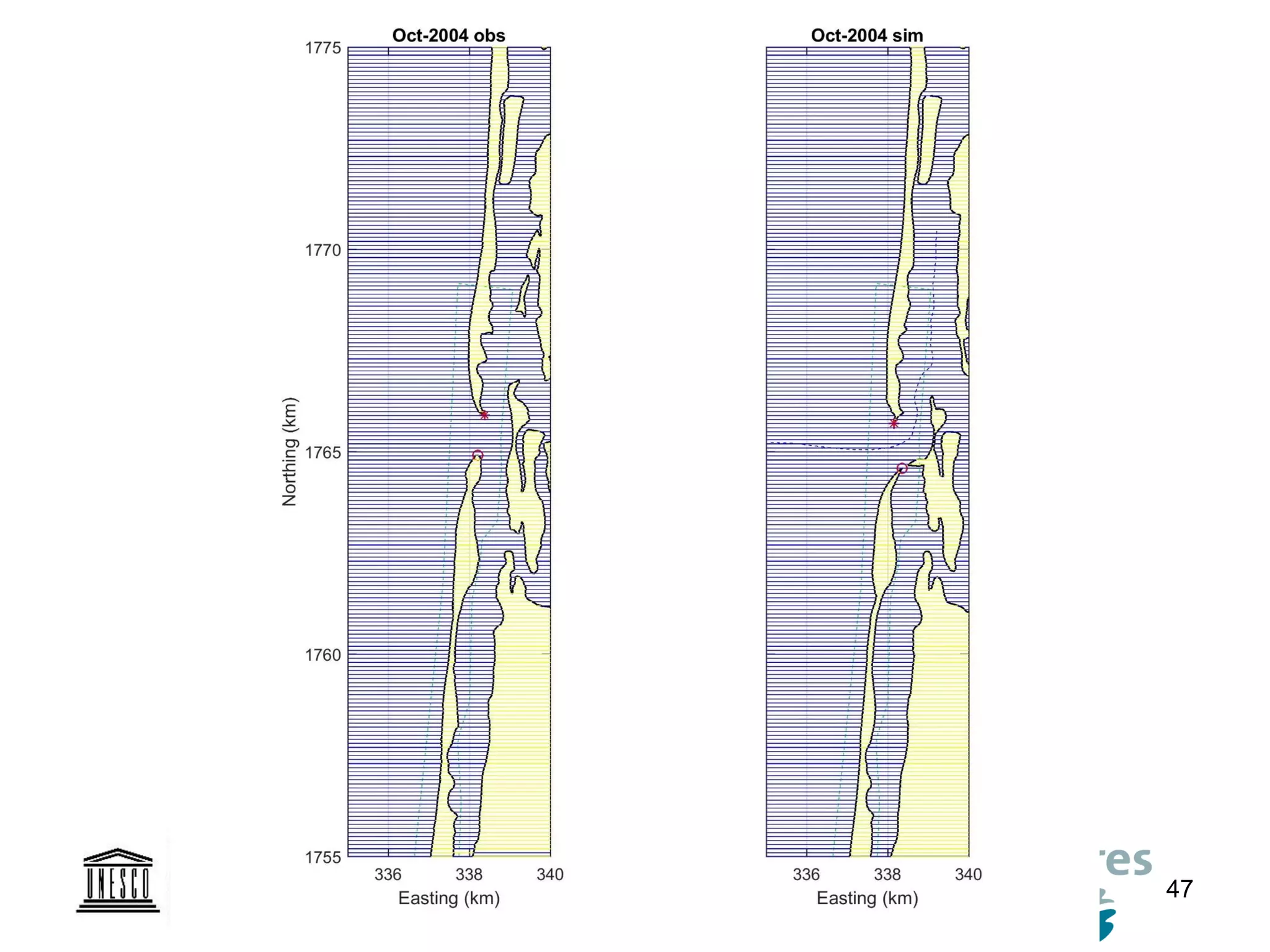
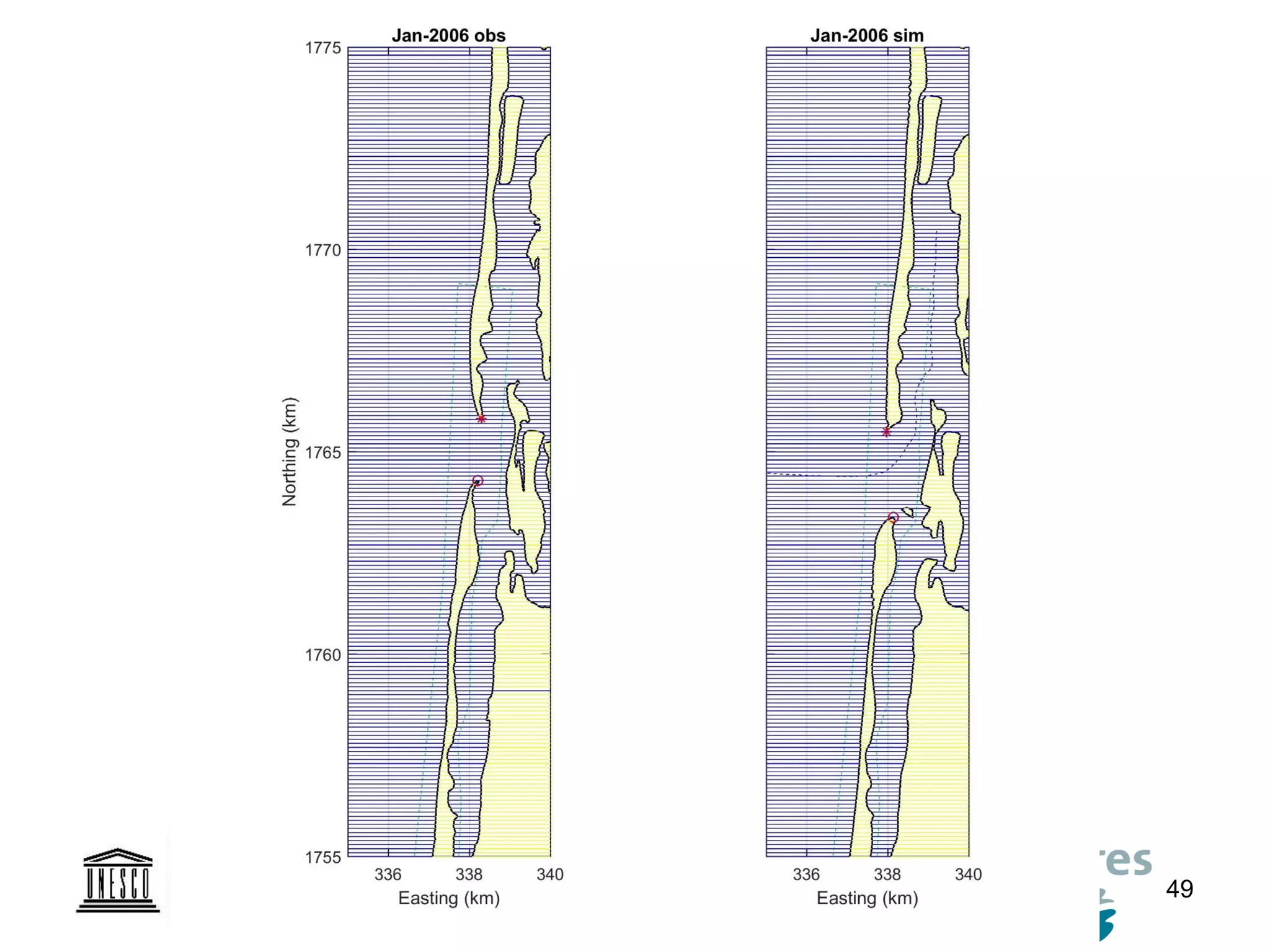
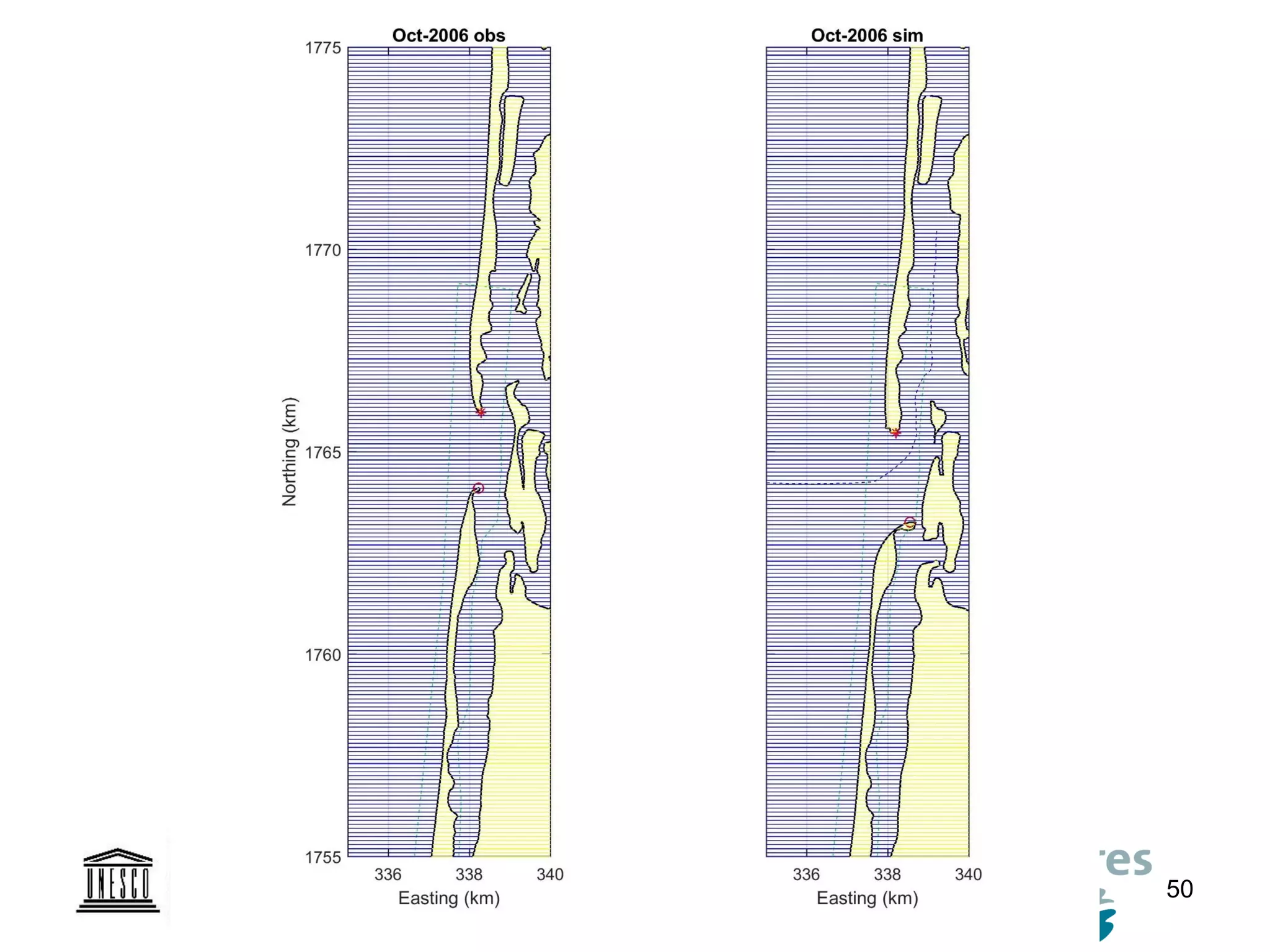
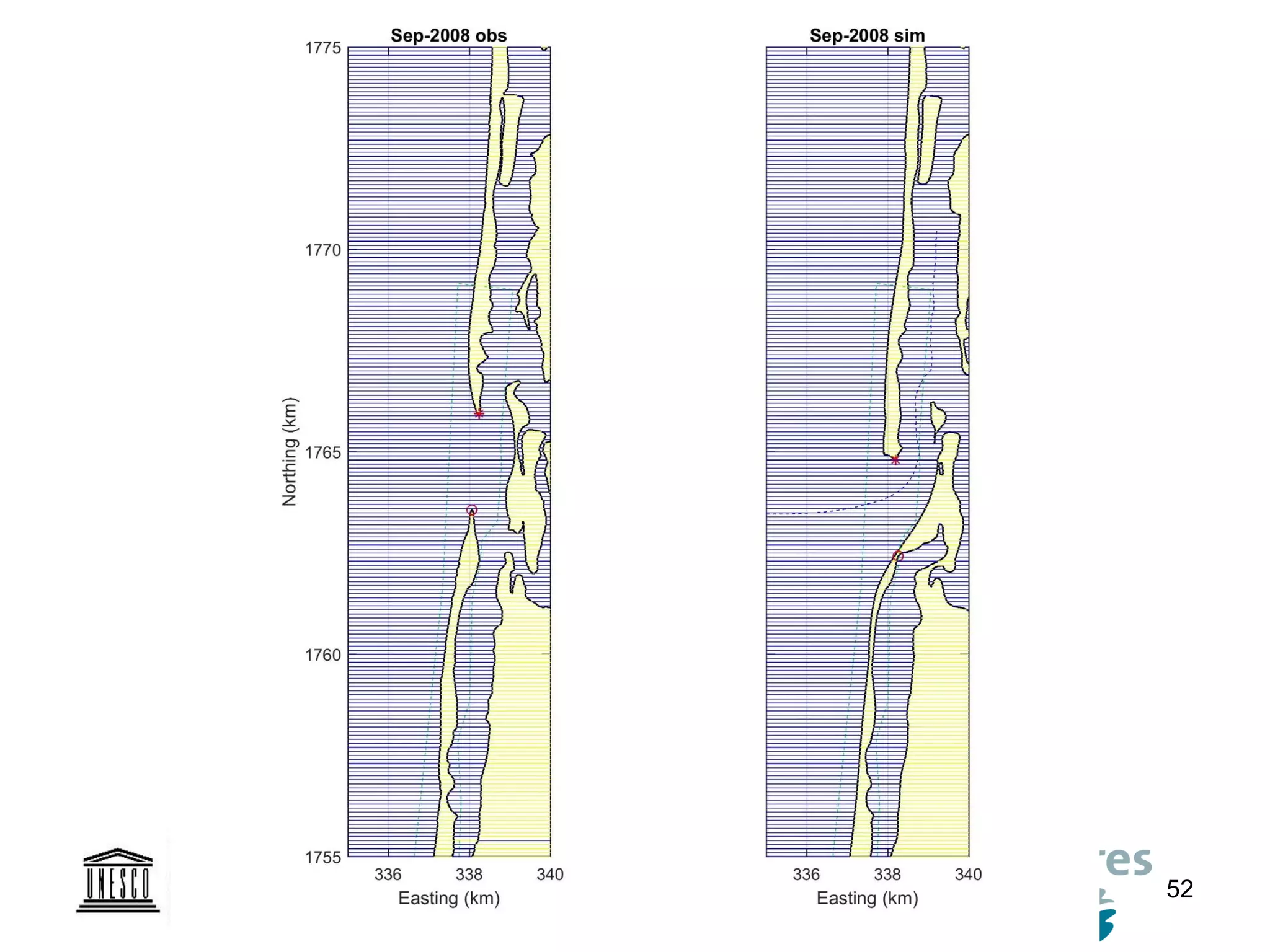
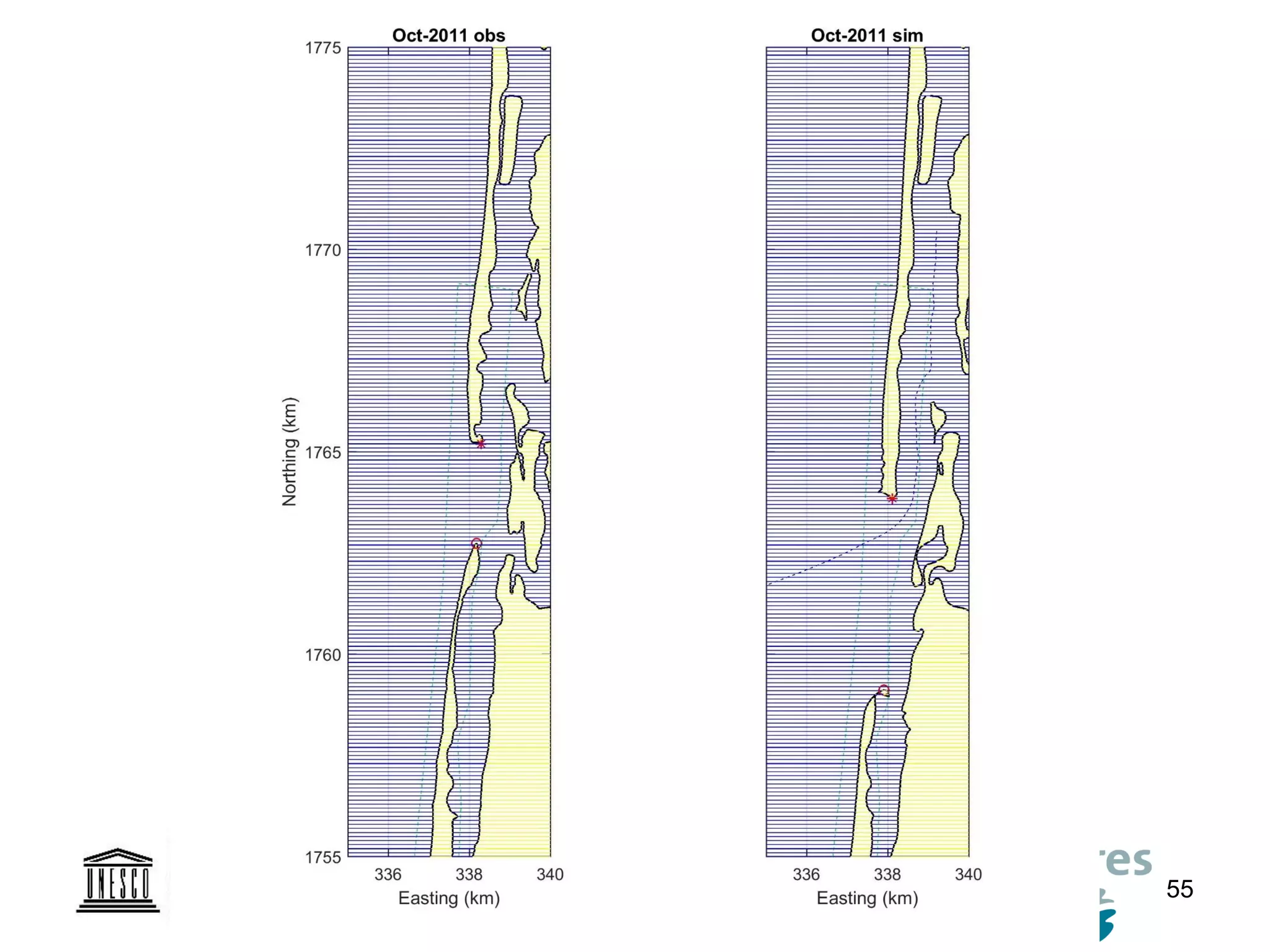
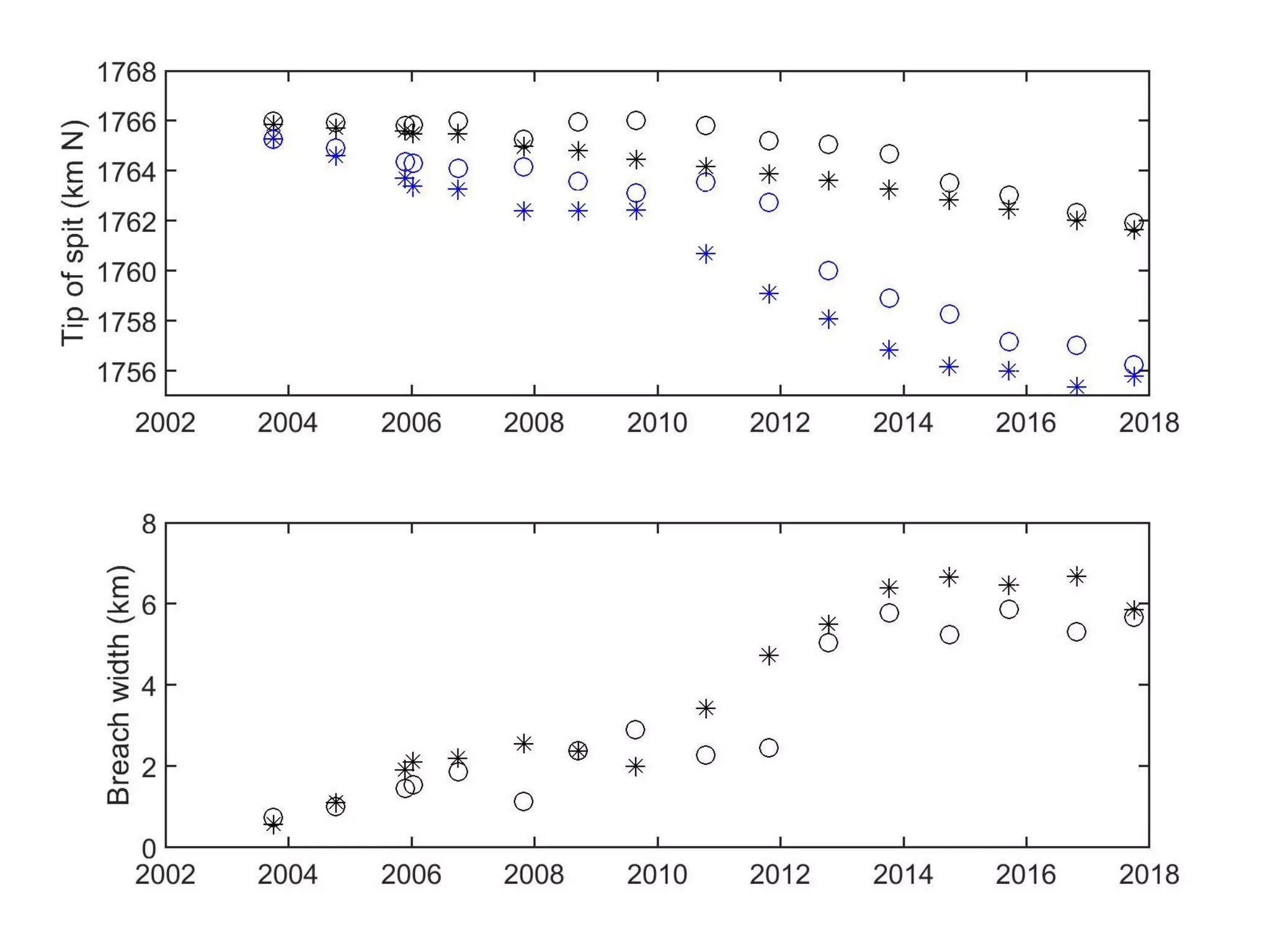
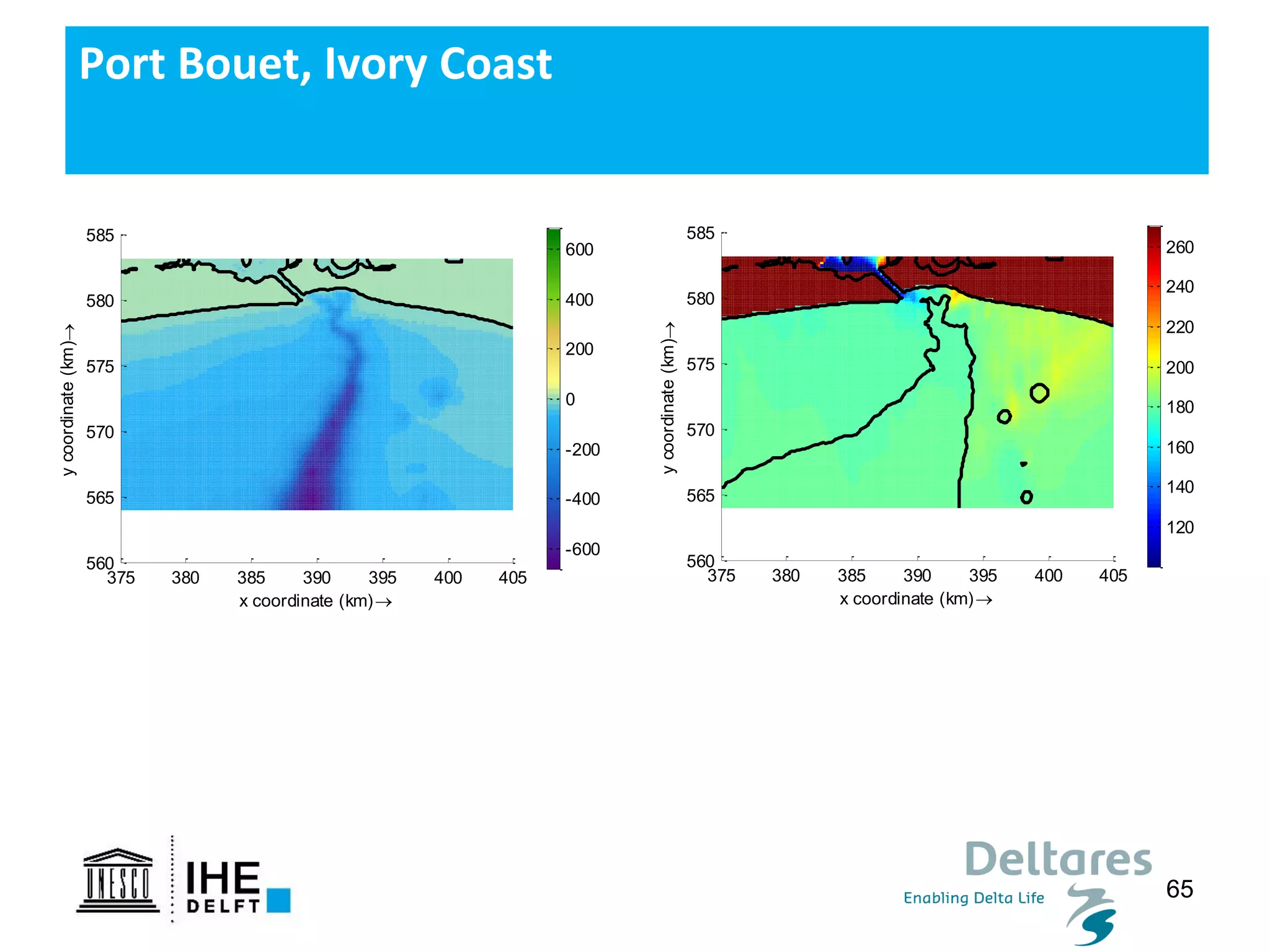
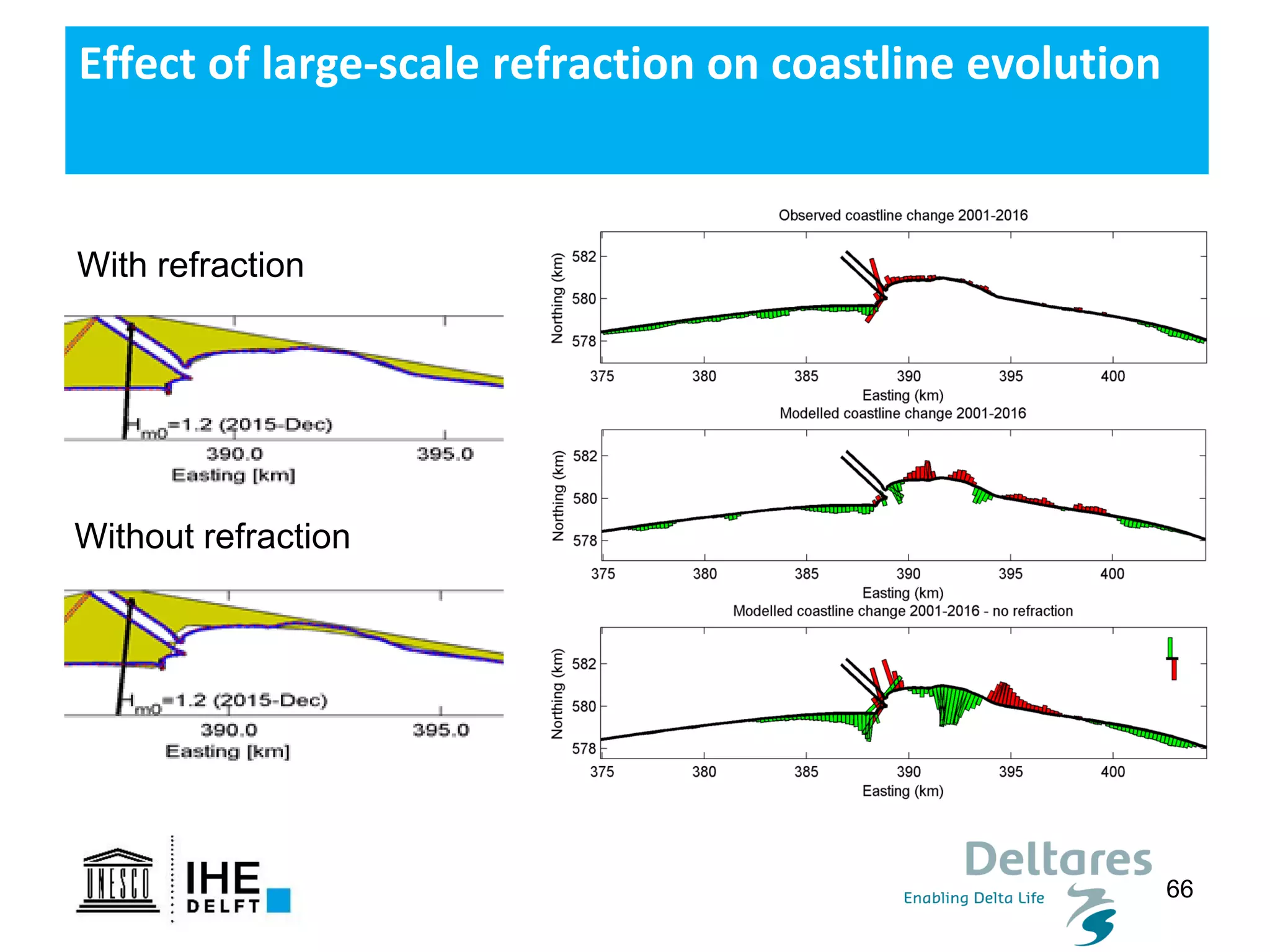
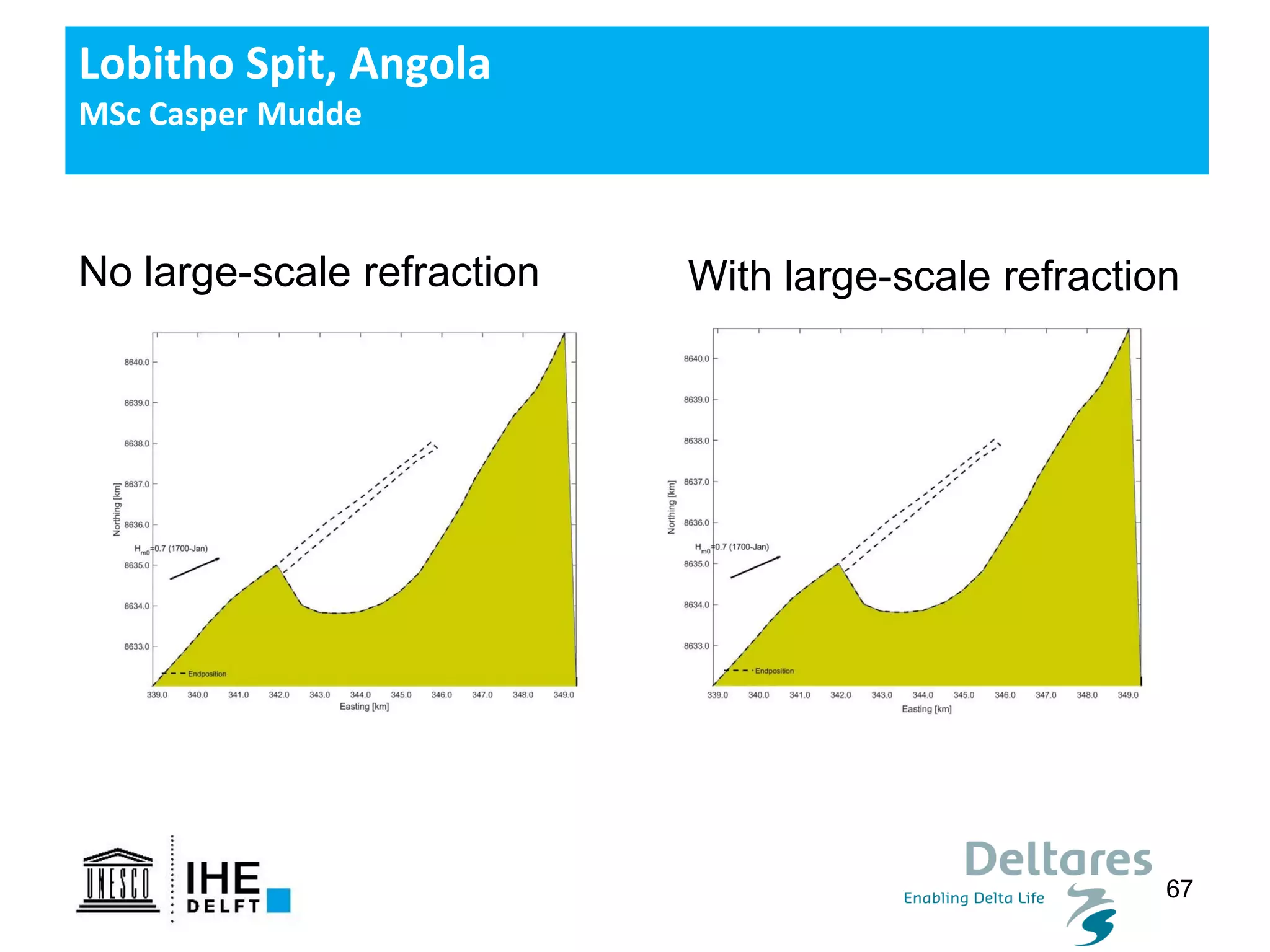
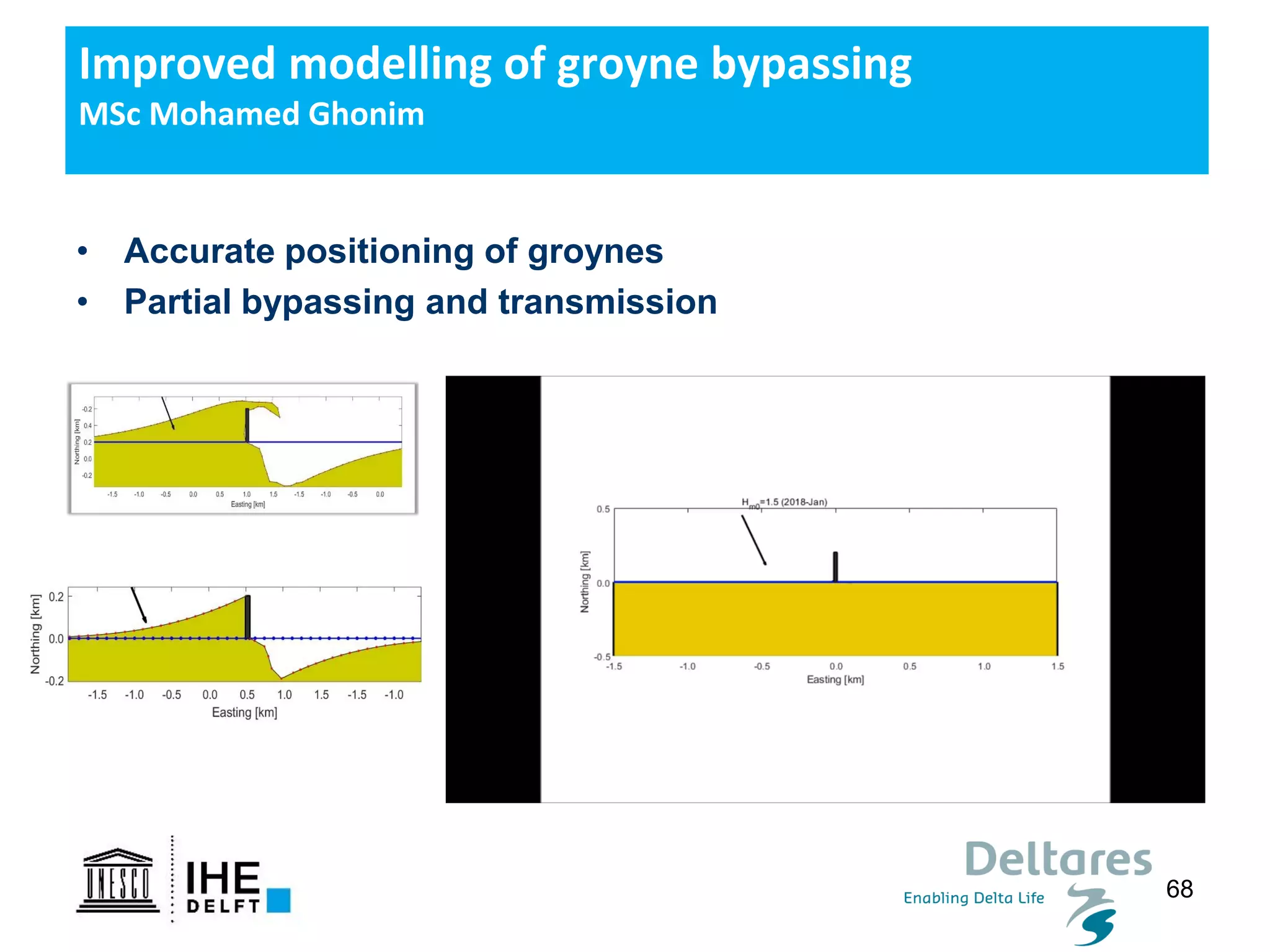
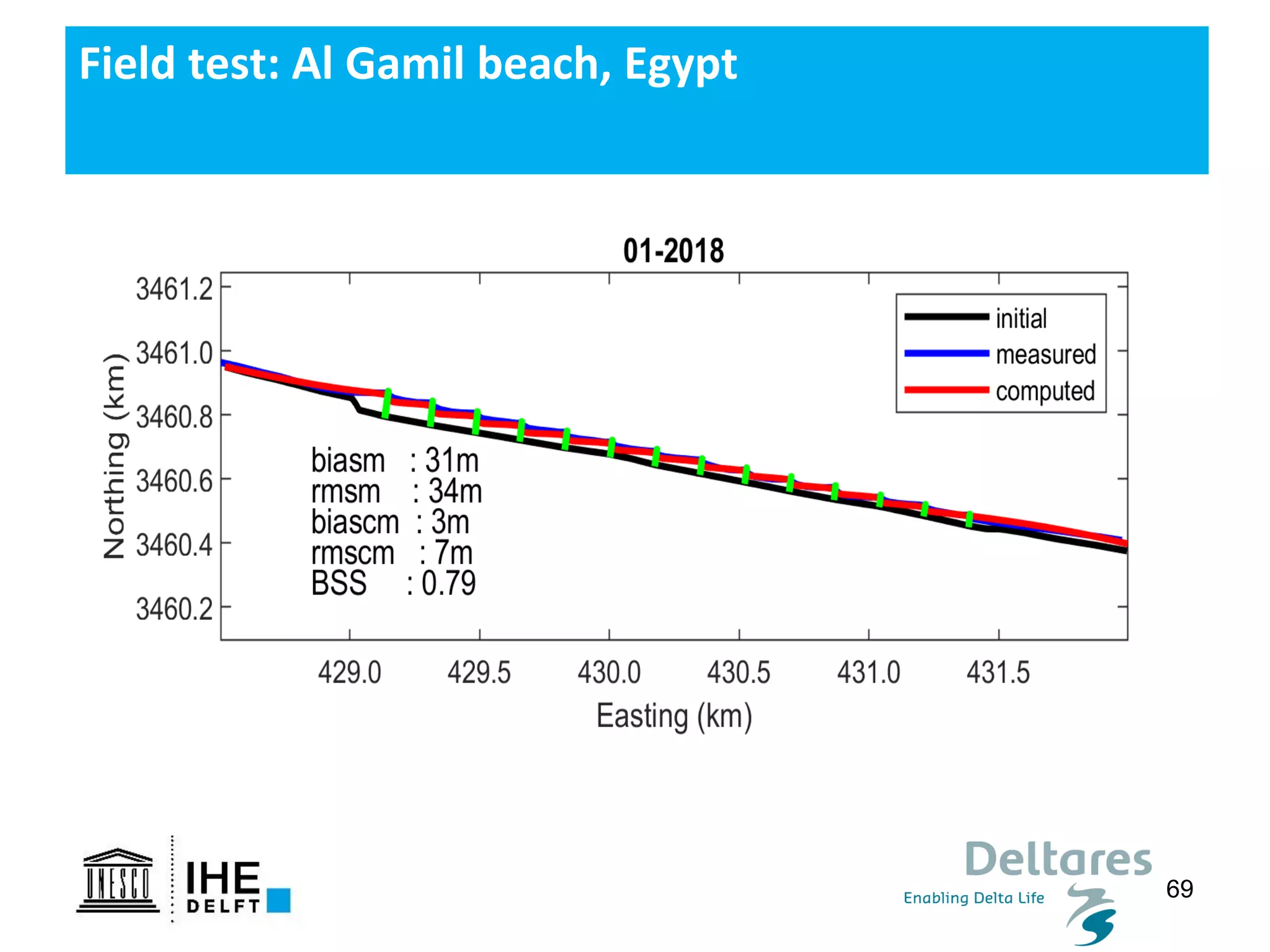
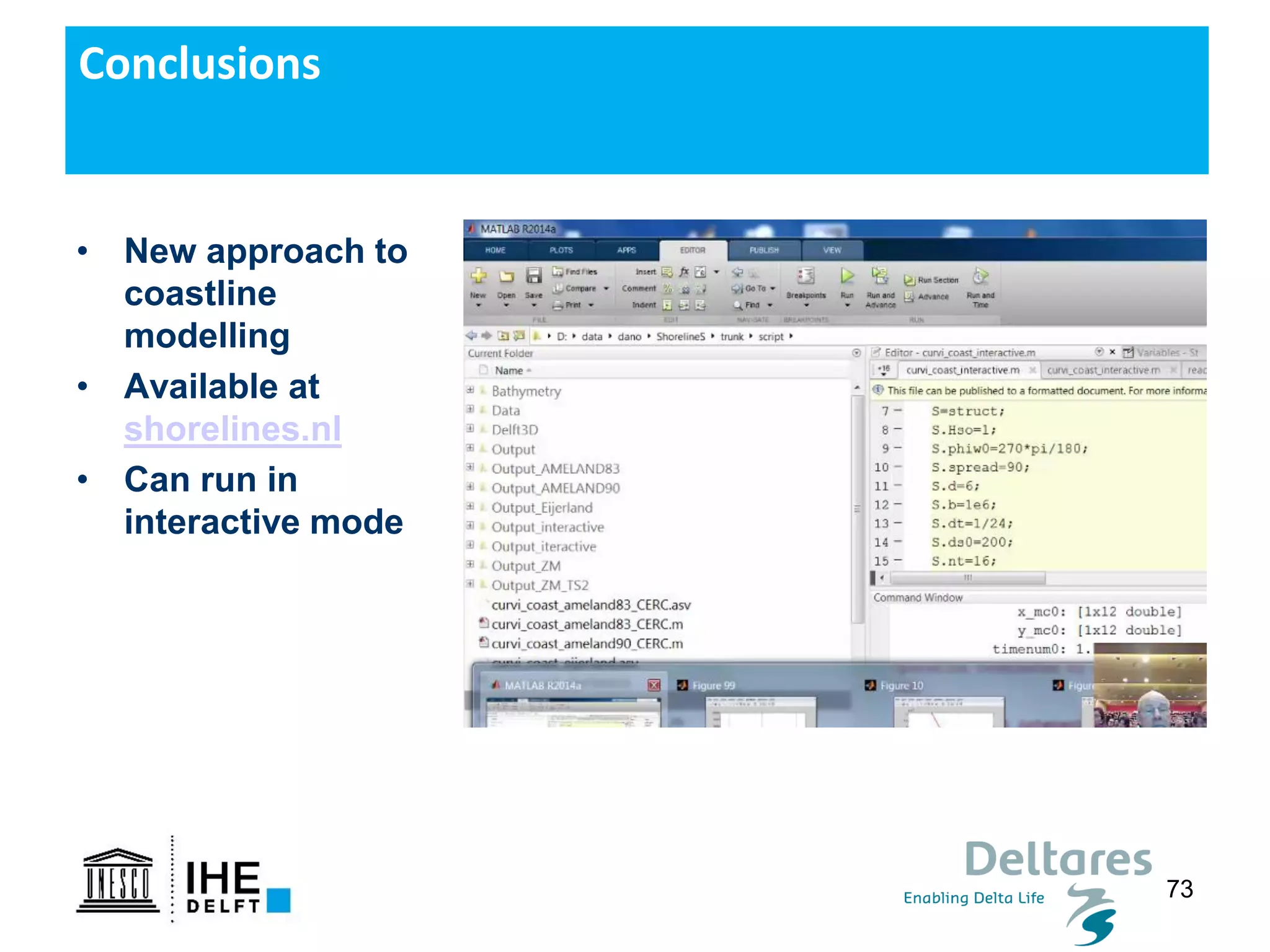
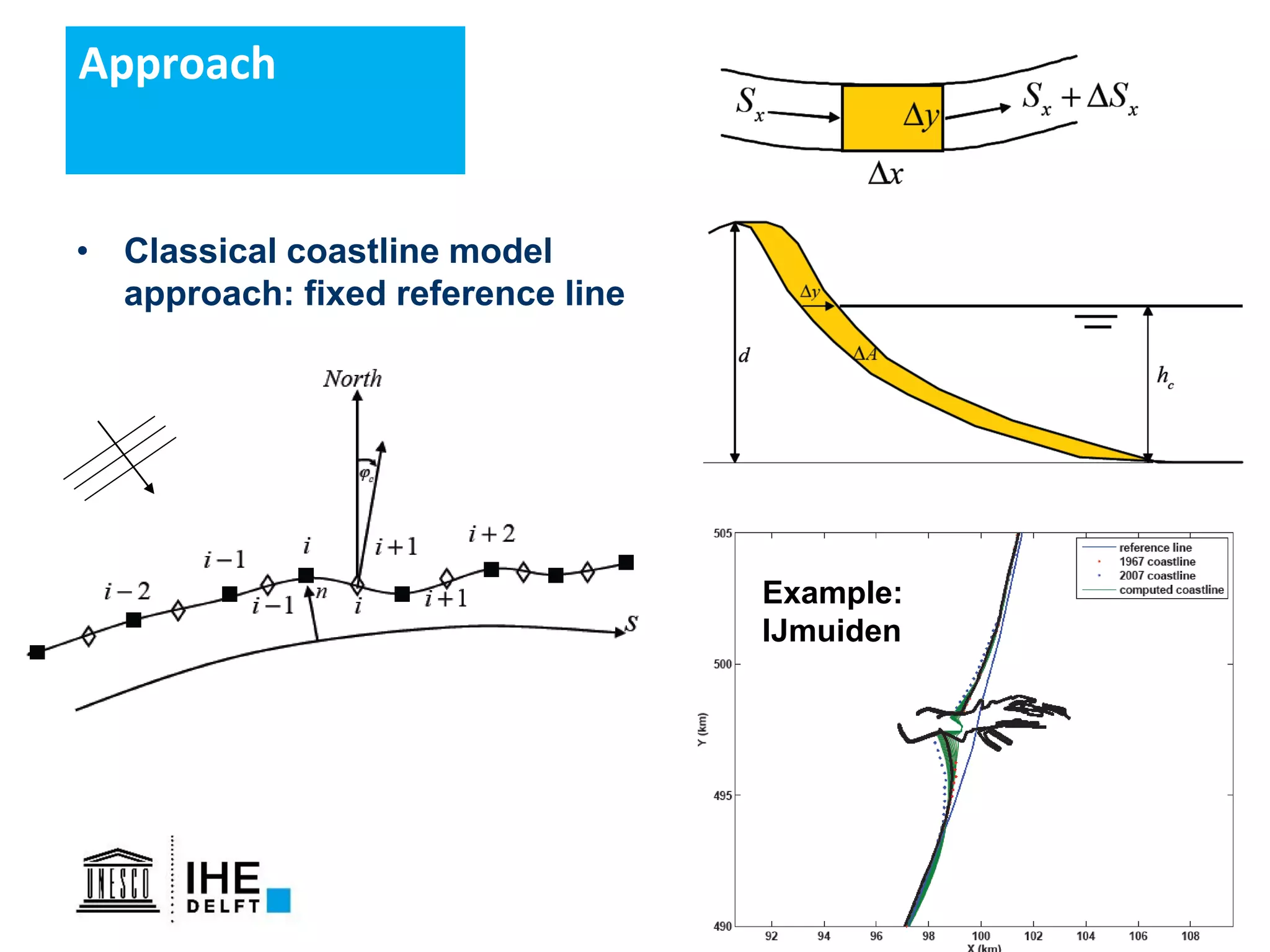
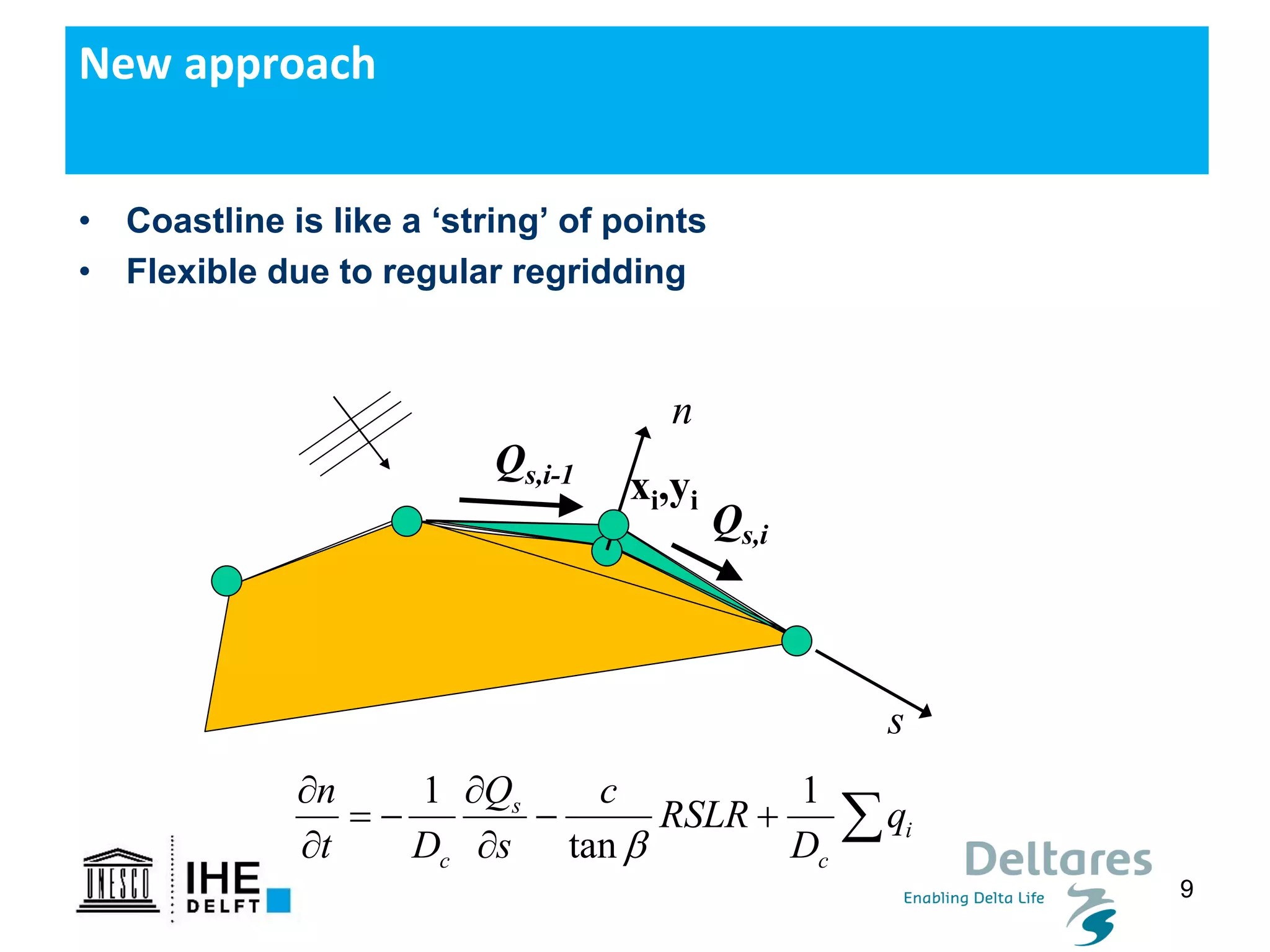
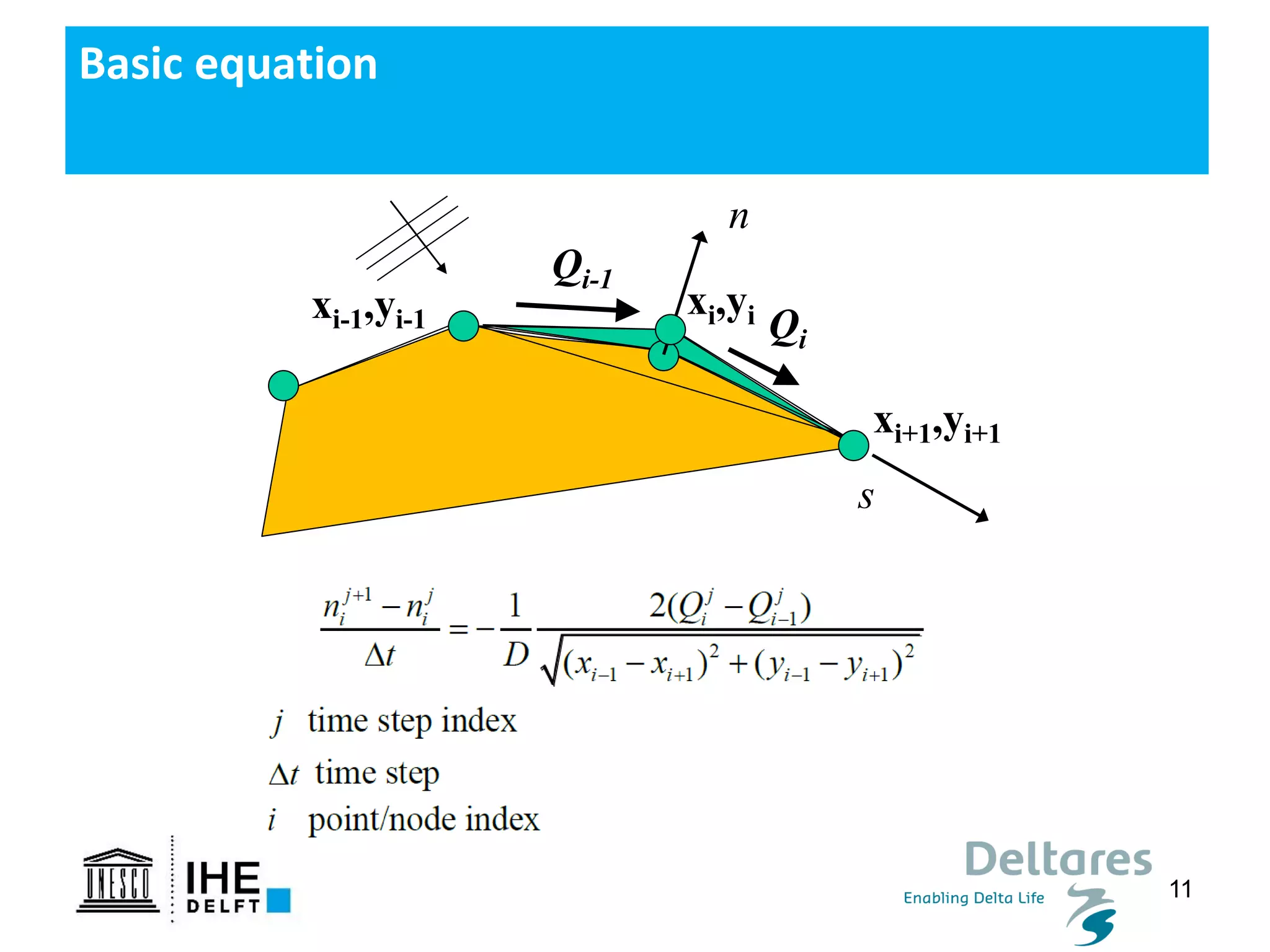
The document discusses the development of a new, more flexible coastline modeling approach to overcome limitations of current models, which are inflexible and inadequate in representing dynamic coastal processes. This new prototype model can effectively simulate complex coastal phenomena, requires minimal input, and is available as open-source MATLAB code. The authors aim to improve accuracy in engineering studies of coastlines while facilitating the integration of additional processes.

1. 1
Dano Roelvink
IHE Delft & DELTARES, Netherlands
ShorelineS and future coastline modelling
Dano Roelvink1,2,3, Bas Huisman2,3 ,
Ahmed Elghandour1,4,5 , Johan Reyns1,3 and
Mohamed Ghonim1
1IHE Delft Institute for Water Education, Delft, The Netherlands
2Deltares, Delft, The Netherlands
3Delft University of Technology, Delft, The Netherlands
4Department of Civil Engineering, Faculty of Engineering, Port
Said University, Port Said, Egypt
5 CIMA, University of the Algarve, Faro, Portugal

2. 2
Motivation
• In complex large-scale systems, resolving the surf zones is
prohibitively expensive on longer timescales
• Coastline modelling has long been a cheap alternative, but
existing models have severe limitations.
• Can we make a better, more flexible coastline model (and
couple it with a 2DH tidal morphology model?)

3. 3
Existing model capabilities: ‘standard’ models
(UNIBEST LT/CL, Litpack, Genesis, CosMoS-COAST)
• Capabilities:
• Wave-driven longshore transport gradients
• Sand mining and sediment delivery by rivers
• Cross-shore transport contributions
• Headlands and structures
• Wide appication in engineering studies
• Limitations:
• Only relatively small changes relative to reference coastline
possible
• No fun processes like spits, islands, migrating inlets, barrier
rollover

4. 4
Szmytkiewicz et al, Coastal Engineering 2000
Intercomparison of coastline models

5. 5
Vitousek et al, JGR-ESP 2017
coastline model of southern California

6. 6
Existing models: Ashton, Murray & Arnault (2001) and
offspring
• Mixture of grid and
coastline
• Simple transport formulas
• Powerful in describing
many types of features
• High-angle instability
important mechanism

7. 7
Pros and cons
• Standard models:
• much experience in engineering
• too inflexible
• not enough processes represented
• CEM and similar models
• beautiful processes represented in elegant way
• relatively complex logic and structure
• only used for schematic system studies
• New, flexible engineering model needed

8. 8
Approach
• Classical coastline model
approach: fixed reference line
Example:
IJmuiden

9. 9
New approach
s
n
Qs,i-1
Qs,i
xi,yi
• Coastline is like a ‘string’ of points
• Flexible due to regular regridding
1 1
tan
s
i
c c
n Q c
RSLR q
t D s D
 
= − − +
 


10. 10
• n is the cross-shore coordinate
• s the longshore coordinate
• Dc the active profile height
• c a coefficient
• the profile slope
• RSLR the relative sea level rise
• qi source/sink terms (m3/m/yr) due to cross-shore transport,
overwashing, nourishments, sand mining and exchanges with
rivers and tidal inlets
New approach
1 1
tan
s
i
c c
n Q c
RSLR q
t D s D
 
= − − +
 

tan𝛽

11. 11
Basic equation
s
n
Qi-1
Qi
xi,yi
xi+1,yi+1
xi-1,yi-1

12. 12
• Simple transport
formulas
• Based on deep water
wave conditions or
conditions at breaker
line
• Similar behaviour as
function of deep water
wave angle
Transport formulations
Author Notation Formula
USACE, 1984
(simplified)
CERC1 5/2
0 sin 2( )s S locQ bH =
Ashton &
Murray, 2006
CERC2 12 1 6
5 5 5
2 0 cos ( )sin( )s S loc locQ K H T  =
USACE, 1984 CERC3 5/2
1 sin2( )s sb locbQ b H =
Kamphuis,
1992
KAMP 2 1.5 0.75 0.25 0.6
502.33 sin (2 )s sb b locbQ H T m D −
=
Where:
b : calibration coefficient CERC1
1
/
, ~ 0.1 0.2
16( )(1 )s
k g k
b k
p

 
= −
− −
( )
sin( )
arctan 2
cos( )
j
j c w
loc i
c w i
 

 
 −
=  
− 
1
5
2 1( )
2
g
K K


= , 1/2
1 0.4 /K m s
0sH : offshore significant wave height
sbH : significant breaking wave height
T : peak wave period
50D : median grain diameter [m]
bm : mean bed slope (beach slope in the breaking zone)
b : breaking wave angle
Author Notation Formula
USACE, 1984
(simplified)
CERC1 5/2
0 sin 2( )s S locQ bH =
Ashton &
Murray, 2006
CERC2 12 1 6
5 5 5
2 0 cos ( )sin( )s S loc locQ K H T  =
USACE, 1984 CERC3 5/2
1 sin2( )s sb locbQ b H =
Kamphuis,
1992
KAMP 2 1.5 0.75 0.25 0.6
502.33 sin (2 )s sb b locbQ H T m D −
=
Where:
b : calibration coefficient CERC1
1
/
, ~ 0.1 0.2
16( )(1 )
k g k
b k
p

 
= −
− −
Transport is a function of wave
height and wave direction
Maximum at around 45o relative to
coast

13. 13
Representation of coastline and structures
• Coastline is represented as an arbitrary number of free-form
polylines that can be open or closed (islands)
0 2000 4000 6000 8000 10000
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
Easting [m]
Northing[m]
Add coastline (LMB); Next segment (RMB); Exit (q)
0 2000 4000 6000 8000 10000
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
Easting [m]
Northing[m]
Add structure (LMB); Next structure (RMB); Exit (q)

14. 14
Wave shadowing
• Waves can be shielded
• by other parts of the same or other coast sections or
• by structures, also represented by polylines
• Sediment transport along the coastlines is driven by a CERC-
like transport formula (based on deep water conditions)
-4000 -2000 0 2000 4000 6000 8000
0
2000
4000
6000
8000
10000
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
0
1000
2000
3000
4000
5000
6000
7000

15. 15
Shadowing

16. 16
• Central scheme becomes unstable when angle >45º
• Upwind scheme creates propagating front as in spit
Upwind correction
Central scheme Upwind scheme

17. 17
Other features
• Coastline changes are computed based on the transport gradients,
with modifications to deal with high-angle instabilities.
• Regridding takes place continuously to allow the growing of spits
and other forms.

18. 18
Overwashing, merging, splitting up
• A set of routines is called every time step to check whether
overwashing takes place, spits get too narrow and break up, or
sections merge.

19. 19
• No spreading
• Spreading 90o
• Spreading 180o
Island merging tests
0 yr 1 yr 2 yr 4 yr3 yr 5 yr 6 yr

20. 20
Van Rijn’s bestiary of coastal forms

21. 21
Sensitivity to resolution

22. 22
Innovative
mega
nourishment
Sand Motor

23. 23
Sand Motor modelled with ShorelineS

24. 24
Sand Motor 2011-2016

25. 25
Error metrics
A
B
C
D
A
B
C
D
E
E

26. 26
St Louis, Senegal
• Small breach to
reduce lagoon
water levels in
2003
• Grew to 5 km
width

27. 27
• Coastlines extracted from LANDSAT imagery
• Long period of southward migration
• Until artificial opening in 2003
• Schematized wave climate
• Mean direction 310 deg N
• Hs = 1.4 m
• Spreading +/- 30 deg
• Simplest CERC formula
• Calibration factor adjusted in calibration
• Problem: inlet closes
Calibration 1984-2003

28. 28
• Two options:
• Implement two-way coupling with a 2DH morphological
model that describes the effect of river flow and tide
• Moving coastline modifies the 2D bathymetry
• Erosion/sedimentation near the coast affects the
coastline
• Implement a heuristic model that
• Maintains width of the channel (could be function of
discharge or tidal prism)
• Pushes back when the coastline moves the channel
centre line
• Distributes the retreat of the narrowest parts towards
neighbouring points
Simulating inlet/river mouth behaviour
Let’s
try this
first

29. 29
Interaction with river mouth/inlet
Green line: original
coast line;
red line : rough input
sketch of river axis ;
blue line :
automatically refined
and moved to exact
center line ;
black line : adjusted
coastlines based on an
equilibrium width of
500 m and adjustment
factor of 0.1.

30. 30

31. 31

32. 32

33. 33

34. 34

35. 35

36. 36

37. 37

38. 38

39. 39

40. 40

41. 41

42. 42

43. 43

44. 44
Spit locations and width of opening

45. 45
St Louis validation 2003-2018
• After artificial breaching
• Initial losses to new flood delta mimicked in heuristic
flood_delta function
• Explains the initial stalling of the migration of the northern spit

46. 46

47. 47

48. 48

49. 49

50. 50

51. 51

52. 52

53. 53

54. 54

55. 55

56. 56

57. 57

58. 58

59. 59

60. 60

61. 61

62. 62

63. 63
• Presence of large-scale features (headlands, shoals, canyons)
can significantly affect shoreline orientation.
• ShorelineS can use a ‘lookup table’ of nearshore wave
conditions defined on a 2D grid
• This can be generated by an offline model such as SWAn or
with an inline wave propagation model
• Example: coastline near Port Bouet, Ivory Coast, which is
influenced by the Trou Sans Fond canyon
Effect of large-scale refraction

64. 64
Port Bouet, Ivory Coast

65. 65
Port Bouet, Ivory Coast
x coordinate (km)→
ycoordinate(km)→
bed level (m)
00-Jan-0000 00:07:10
375 380 385 390 395 400 405
560
565
570
575
580
585
-600
-400
-200
0
200
400
600
x coordinate (km)→
ycoordinate(km)→
bed level (m)
00-Jan-0000 00:03:10
375 380 385 390 395 400 405
560
565
570
575
580
585
120
140
160
180
200
220
240
260

66. 66
Effect of large-scale refraction on coastline evolution
With refraction
Without refraction

67. 67
Lobitho Spit, Angola
MSc Casper Mudde
No large-scale refraction With large-scale refraction

68. 68
Improved modelling of groyne bypassing
MSc Mohamed Ghonim
• Accurate positioning of groynes
• Partial bypassing and transmission

69. 69
Field test: Al Gamil beach, Egypt
Shoreline 2011
Shoreline 2013
Shoreline 2015
Shoreline 2017
Shoreline 2018
1
2
3
4
5
6
7
8
9
10
11
12
13
14
100 m 300m200 m0 m

70. 70
Conclusions ShorelineS
• Fun new model
• Prototype for next generation coastline model for engineering
purposes
• Is available in open source Matlab code
• Great for explaining coastal processes
• Easy to add more processes
• Needs very little input that is readily available:
• Initial coastline
• Rocky parts or structures
• Wave climate

71. 71
• Coupling with dune foot (Mohamed)
• Barrier overwashing and rollover (Ahmed)
• Tidal inlet migration (Dano, Ahmed)
• Wave diffraction (Ahmed)
• Large-scale wave refraction (Bas, Casper, Dano)
• Ensemble Kalman Filter (Shadrack, Johan, Sean)
• Case studies in Portugal, Alaska, Senegal, Angola, NL
Current research

72. 72
• What would you like to add
• What cases could you bring
• What could be the ambition
• How would you like to use it
• …
Over to you…

73. 73
• New approach to
coastline
modelling
• Available at
shorelines.nl
• Can run in
interactive mode
Conclusions