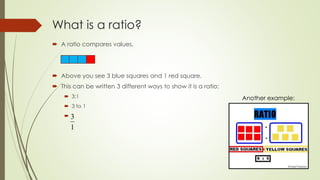
This document discusses ratios and proportions. It defines a ratio as a comparison of values and shows examples of ratios written in different formats like 3:1 or 3 to 1. Ratios can be scaled up or down by multiplying both values by the same number. A proportion is a statement that two ratios are equal to each other. To determine if ratios form a proportion, you cross multiply the terms - if you get the same number, the ratios are proportional; if the numbers are different, they are not proportional. Examples are provided to illustrate determining proportionality through cross multiplying.

1. Do ratios form a
proportion?

2. What is a ratio?
 A ratio compares values.
 Above you see 3 blue squares and 1 red square.
 This can be written 3 different ways to show it is a ratio:
 3:1
 3 to 1

1
3
Another example:

3. Scale up or scale down . . .
 A ratio can always be scaled up or scaled down.
 For example:
 3:1 is the same as 6:2
 It may be easier to see if you think of it like equivalent fractions and set them
equal:
2
6
1
3
 Here the numerator (top) and denominator (bottom)
are both multiplied by 2 so the ratio is still the same.

4. Proportion
 A proportion says that two ratios are equal.
 Example:
 Another example:
4
2
2
1

3
1
12
4


5. How do you know if ratios form a
proportion?
 Remember a proportion is a statement that two ratios are equal.
 When you are given a problem the way to check to see if they are
proportional is to cross multiply:
 20 * 5 =100
 25 * 4 = 100
5
4
25
20

We need to check to see if these are proportional.
- First cross multiply
- Then we see if we get the same number.
- If we have the same number they are proportional.
100 = 100
So these are proportional!

6. Let’s look at a few more examples . . .
 Are the ratios below proportional?
 Cross multiply first
 8 * 40 = 320
 10 * 32 = 320
 You end up with the same
number.
 Are the ratios below proportional?
 Cross multiply first
 10 * 5 = 50
 20 + 4 = 80
 You do not have the same
number.
40
32
10
8

320=320
So they are proportional!
5
4
20
10

50 ≠ 80
So they are NOT proportional!