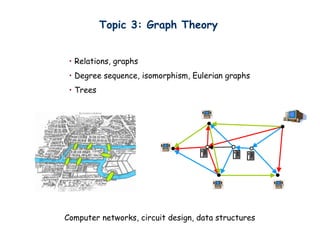
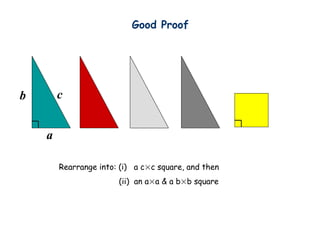
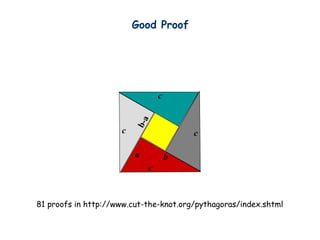
The document outlines a course on discrete mathematics for computer science, detailing the syllabus, materials, and evaluation criteria. Key topics include logic, counting, graph theory, and number theory, which serve as foundations for efficient computer system design, algorithms, and internet security. The course employs a textbook and includes assessments such as homework, quizzes, exams, and potential bonus questions.

1. Discrete Structures for
Computer Science
Ruoming Jin
MW 2:15 – 3:00pm
Spring 2010
rm MSB115

2. Course Material
 Textbook: Discrete Mathematics and Its Applications
 Kenneth H. Rosen, McGraw Hill

3. Course Requirements
 Homework, 20%
 Quiz, 20%
Three Intermediate Exams: 10%
 Final Exam, 30%
 Bonus Questions 5-10%

4. Why Discrete Math?
Design efficient computer systems.
•How did Google manage to build a fast search engine?
•What is the foundation of internet security?
algorithms, data structures, database,
parallel computing, distributed systems,
cryptography, computer networks…
Logic, sets/functions, counting, graph theory…

5. What is discrete mathematics?
logic, sets, functions, relations, etc
Logic: artificial intelligence (AI), database, circuit design
Counting: probability, analysis of algorithm
Graph theory: computer network, data structures
Number theory: cryptography, coding theory

6. Topic 1: Logic and Proofs
Logic: propositional logic, first order logic
Proof: induction, contradiction
How do computers think?
Artificial intelligence, database, circuit, algorithms

7. Topic 2: Counting
• Sets
• Combinations, Permutations, Binomial theorem
• Functions
• Counting by mapping, pigeonhole principle
• Recursions, generating functions
Probability, algorithms, data structures

8. Topic 2: Counting
How many steps are needed to sort n numbers?

9. Topic 3: Graph Theory
• Relations, graphs
• Degree sequence, isomorphism, Eulerian graphs
• Trees
Computer networks, circuit design, data structures

10. Topic 4: Number Theory
• Number sequence
• Euclidean algorithm
• Prime number
• Modular arithmetic
Cryptography, coding theory, data structures

11. 2 2 2
a b c
 
Familiar?
Obvious?
c
b
a
Pythagorean theorem

12. c
b
a
Rearrange into: (i) a cc square, and then
(ii) an aa & a bb square
Good Proof

13. c
c
c
a b
c
b
-
a
Good Proof
81 proofs in http://www.cut-the-knot.org/pythagoras/index.shtml