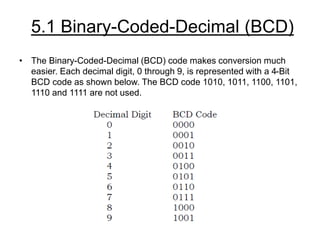
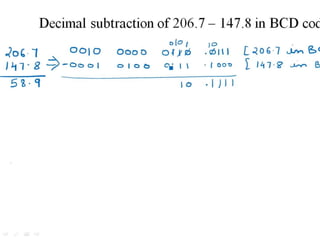
The document discusses 1's and 2's complement in the binary number system, explaining how to calculate them with given binary examples. It then introduces binary-coded decimal (BCD) as a method to simplify conversions between decimal and binary, detailing the representation of each decimal digit with a 4-bit BCD code. Additionally, it covers BCD addition and subtraction techniques, outlining corrections needed for invalid codes or borrowing during operations.

1. 1’s and 2’s complement

2. • Binary number system is the type of most
popular Number Representation
techniques that used in digital systems.
• In the Binary System, there are only two
symbols or possible digit values, i.e., 0 (off)
and 1 (on). Represented by any device that
only 2 operating states or possible conditions.

3. 1’s complement
• 1’s complement of a given binary number is
obtained by replacing 1 instead of 0 and 0
instead of 1
Find out 1’s complement of binary number
• 101101 1’s complement is 010010
• 111001 1’s complement is 000110
• 01010110 1’s complement is 10101001

4. • Example-1: Find 1’s complement of binary
number 10101110.
• Example-2: Find 1’s complement of binary
number 10001.001.
• Example-3: Find 1’s complement of each 3 bit
binary number.

5. 2’s complement
• 2’s complement of a given binary number is obtained
by adding1 to 1’s complement
Find out 2’s complement of binary number
• 101101
1’s complement is 010010
2’s complement is 010010+1=010011
• 111001
1’s complement is 000110
2’s complement is 000110+1=000111
• 01010110
1’s complement is 10101001
2’s comp.. is 10101001+1=10101010

6. 5.0 Binary-Coded-Decimal (BCD)
• Conversions between decimal and binary can become long and
complicated for large numbers.
• For example, convert 87410 to binary. The answer is 11011010102,
but it takes quite a lot of time and effort to make this conversion. We
call this straight binary coding.

7. 5.1 Binary-Coded-Decimal (BCD)
• The Binary-Coded-Decimal (BCD) code makes conversion much
easier. Each decimal digit, 0 through 9, is represented with a 4-Bit
BCD code as shown below. The BCD code 1010, 1011, 1100, 1101,
1110 and 1111 are not used.

8. • Conversion between BCD and decimal is accomplished by replacing
a 4-bit BCD for each decimal digit. For example, 87410 = 1000 0111
0100BCD.
• BCD is not another number system like binary, octal, decimal and
hexadecimal. It is in fact the decimal system with each digit encoded
in its binary equivalent. A BCD code is not the same as a straight
binary number. For example, the BCD code requires 12 bits, while
the straight binary number requires only 10 bits to represent 87310.
5.2 Decimal  BCD Conversion

9. • A BCD code is converted into a decimal number by taking groups of
4 bits, starting from LSB, and replacing them with a BCD code. For
example, 1 1001 0111 1000 BCD = 197810
5.3 BCD  Decimal Conversion

10. BCD ADDITION:-
• Addition of BCD (8421) is performed by
adding two digits of binary, starting from least
significant digit. In case if
• the result is an illegal code (greater than 9) or
if there is a carry out of one then add 0110(6)
and add the
• resulting carry to the next most significant.

12. BCD SUBTRACTION:-
• The BCD subtraction is performed by subtracting
the digits of each 4 – bit group of the subtrahend
from corresponding 4 – bit group of the minuend
in the binary starting from the LSD.
• If there is no borrow from the next higher group
then no correction is required. If there is a
borrow from the next group, then 6 (0110) is
subtracted from the difference term of this
group.
• For example:-
• Subtract 147.8 from 206.7 using 8421 BCD code.