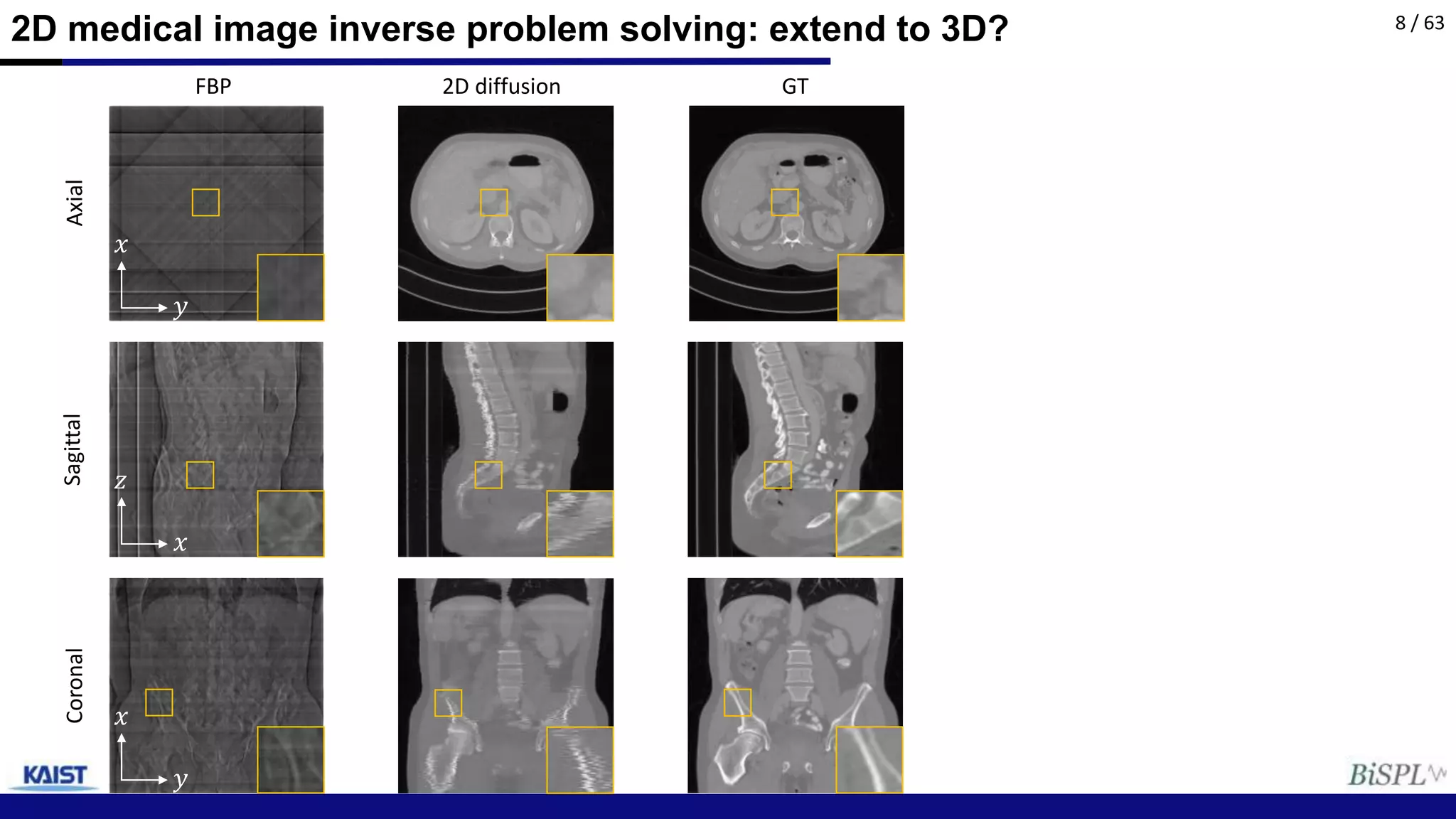
This document proposes a method called Fast DiffusionMBIR to solve 3D inverse problems using pre-trained 2D diffusion models. It augments the 2D diffusion prior with a model-based total variation prior to encourage consistency across image slices. The method performs denoising across image slices in parallel using a 2D diffusion score function, and then jointly optimizes data consistency and the total variation prior between slices. It shares primal and dual variables between iterations for faster convergence. Results on sparse-view CT reconstruction show coherent volumetric results across all slices.

![http://yang-song.github.io/blog/2021/score/
Background: Diffusion models and Stein score
Explicit score matching
Denoising score matching
Equivalent (Vincent et al. 2010)
𝜽∗
= argmin
𝜽
𝔼[‖∇𝐱log 𝑝 𝐱 − 𝐬𝜽(𝐱)‖2
2
]
𝜽∗ = argmin
𝜽
𝔼[‖∇𝐱log 𝑝 𝐱 | 𝐱 − 𝐬𝜽(𝐱)‖2
2
]
2 / 63](https://image.slidesharecdn.com/diffusionmbirpresentationslide-230313023314-a5670ea9/75/DiffusionMBIR_presentation_slide-pptx-2-2048.jpg)