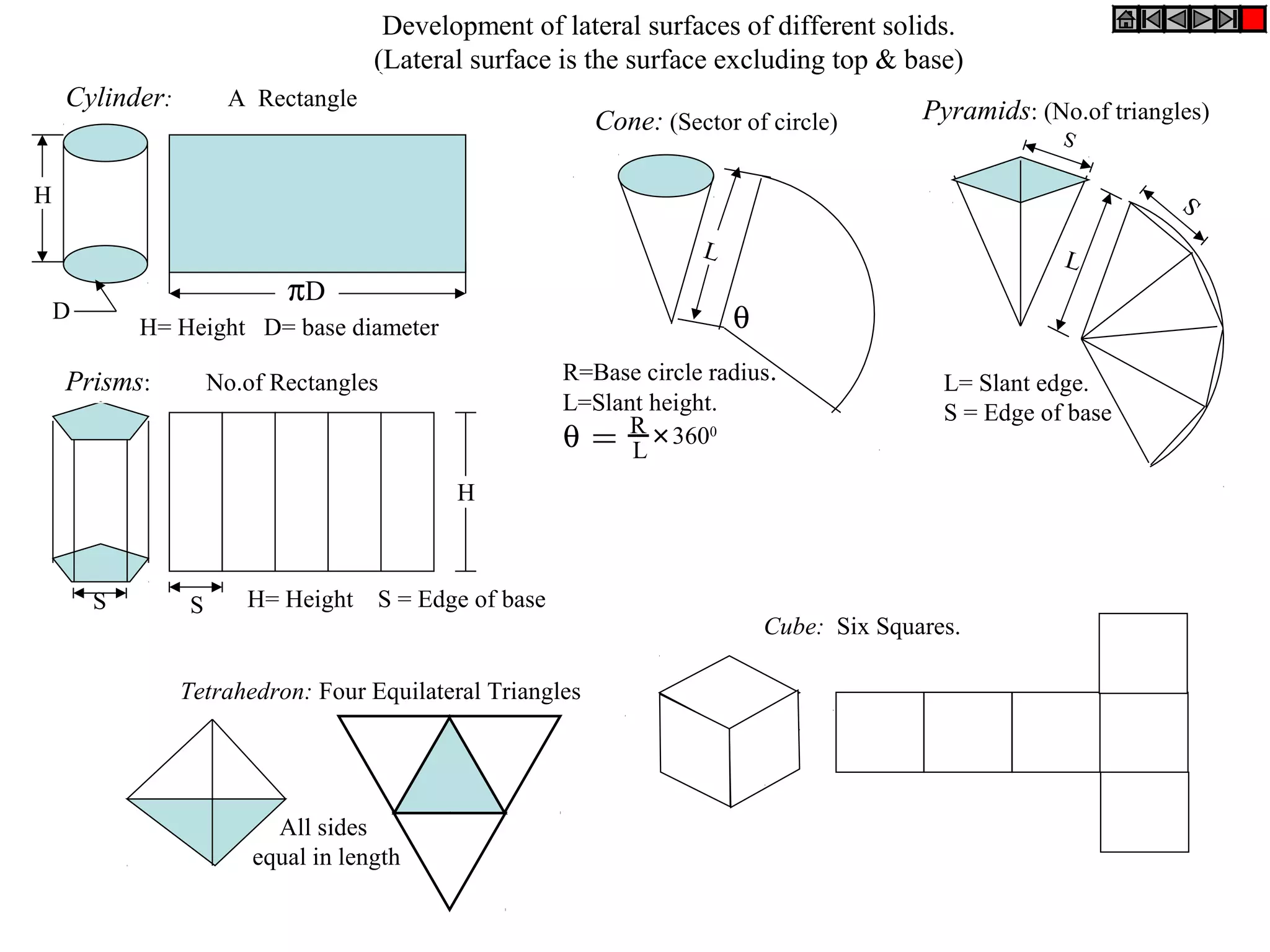
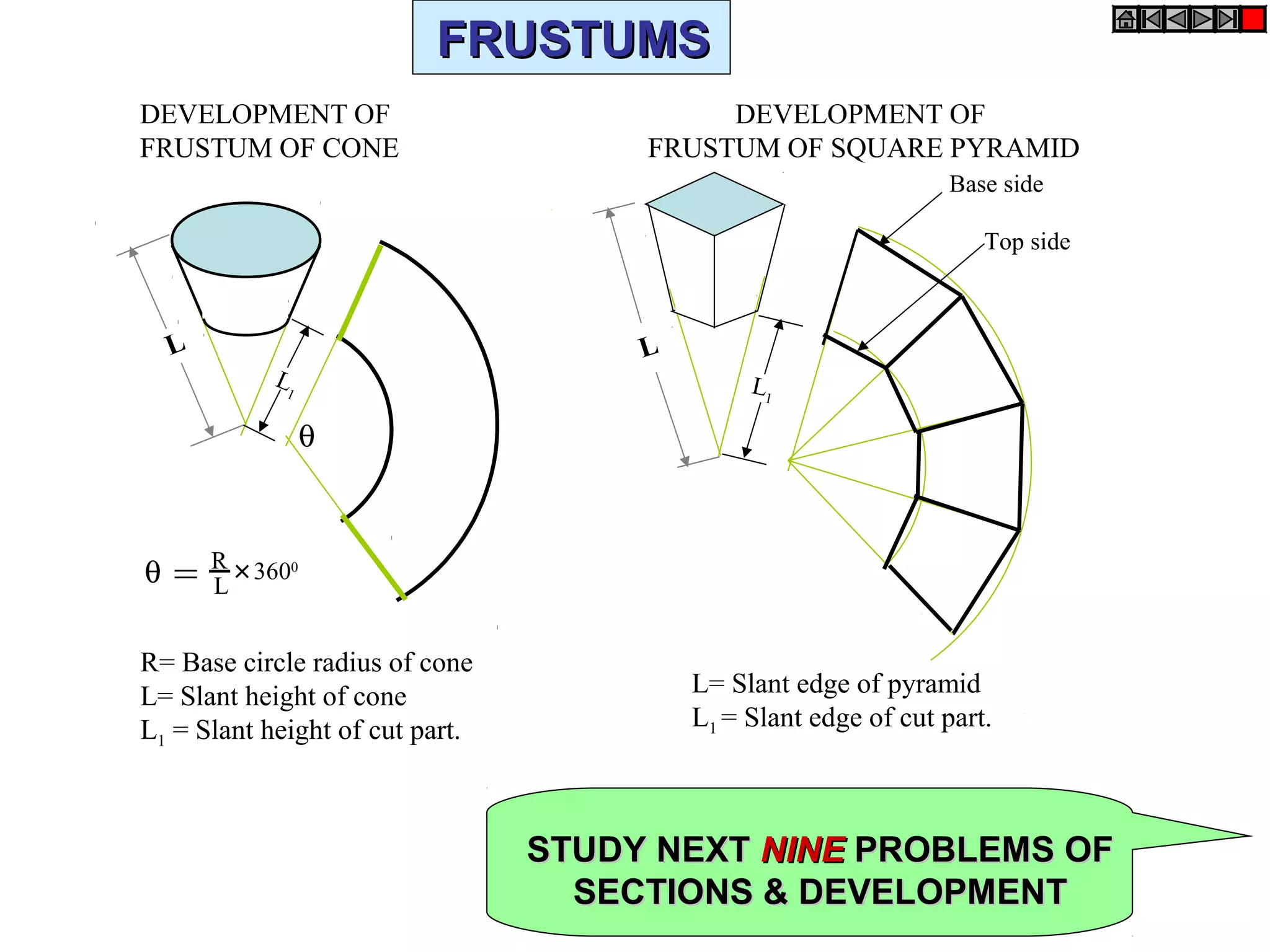
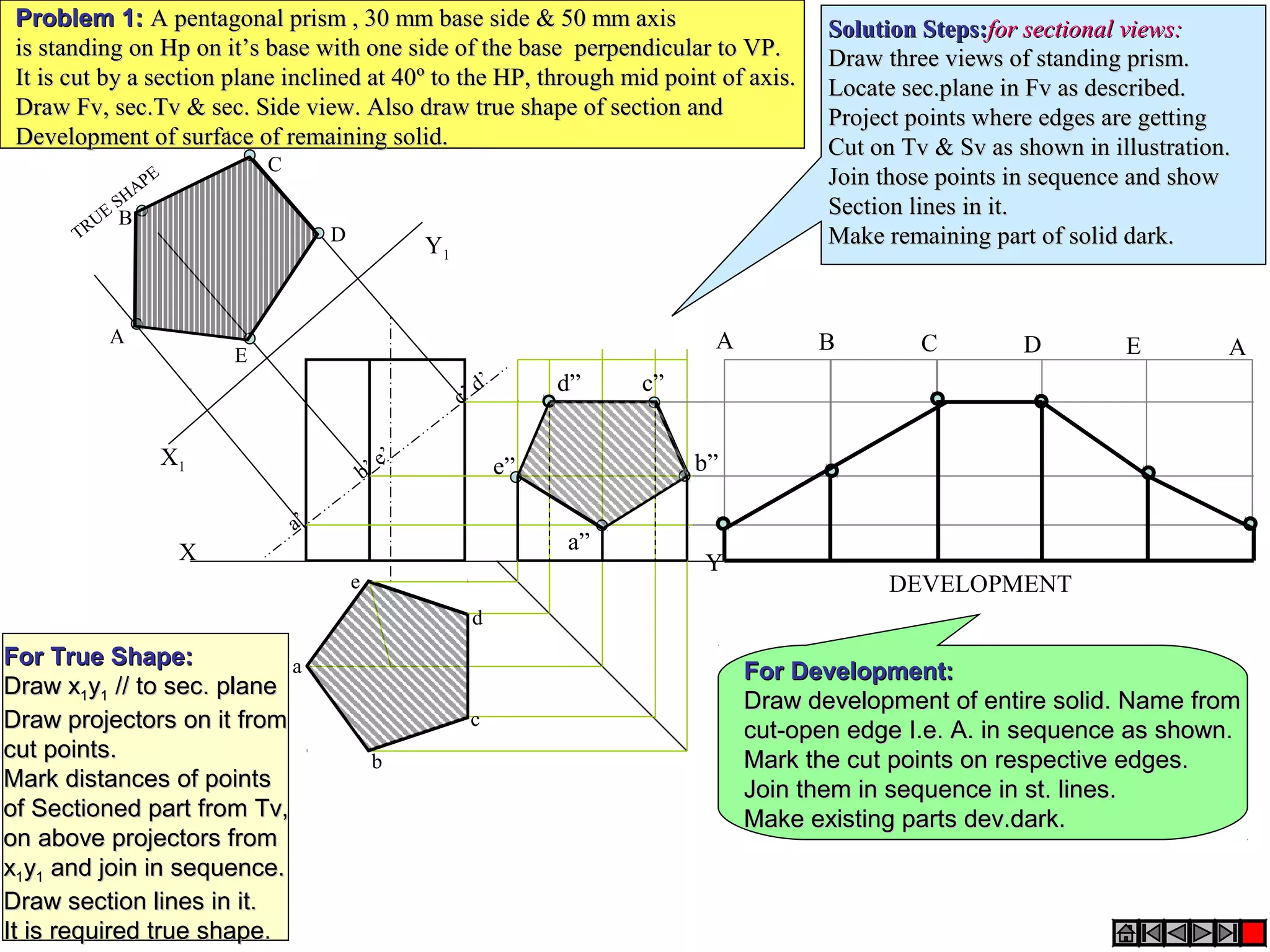
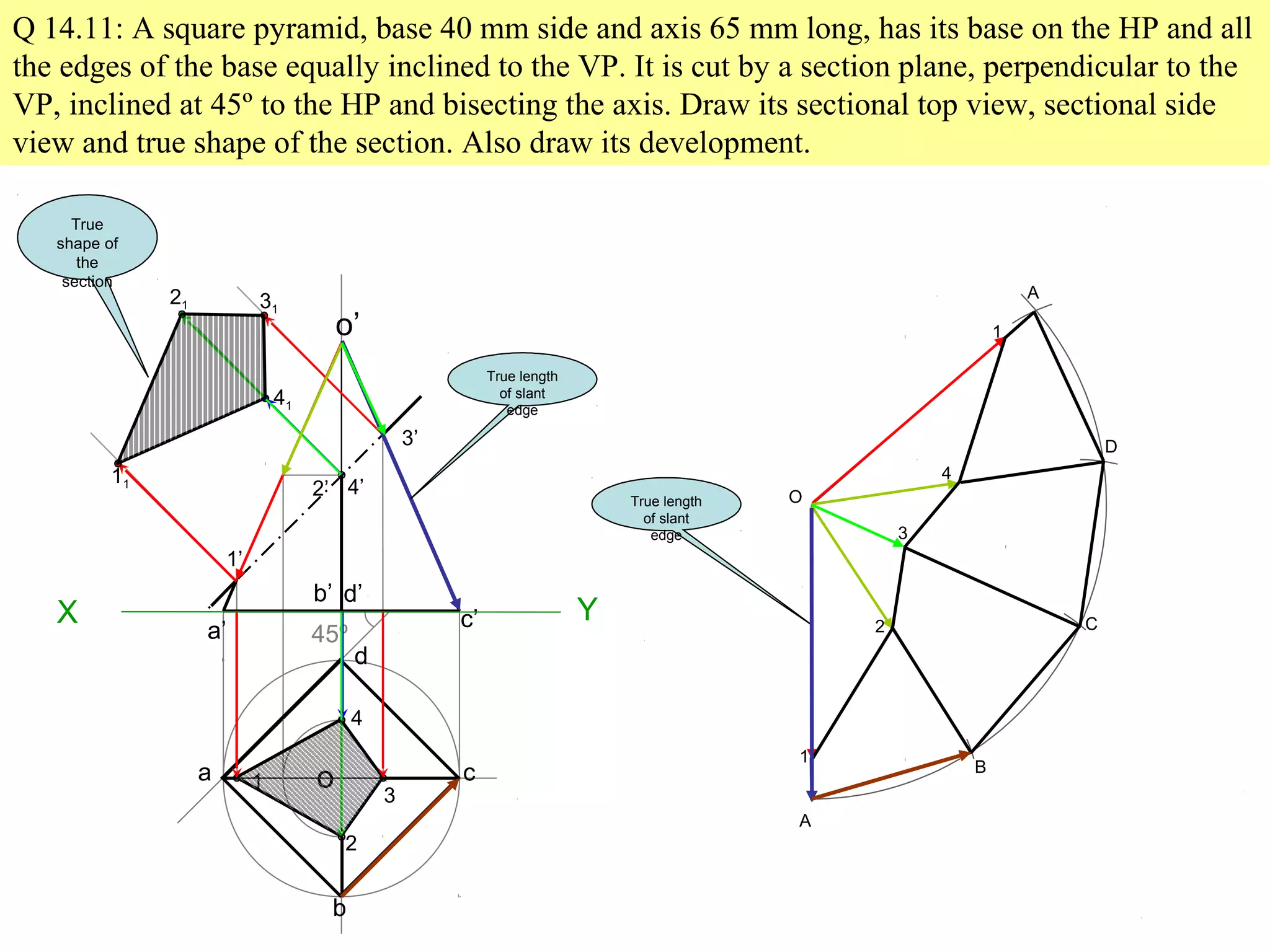
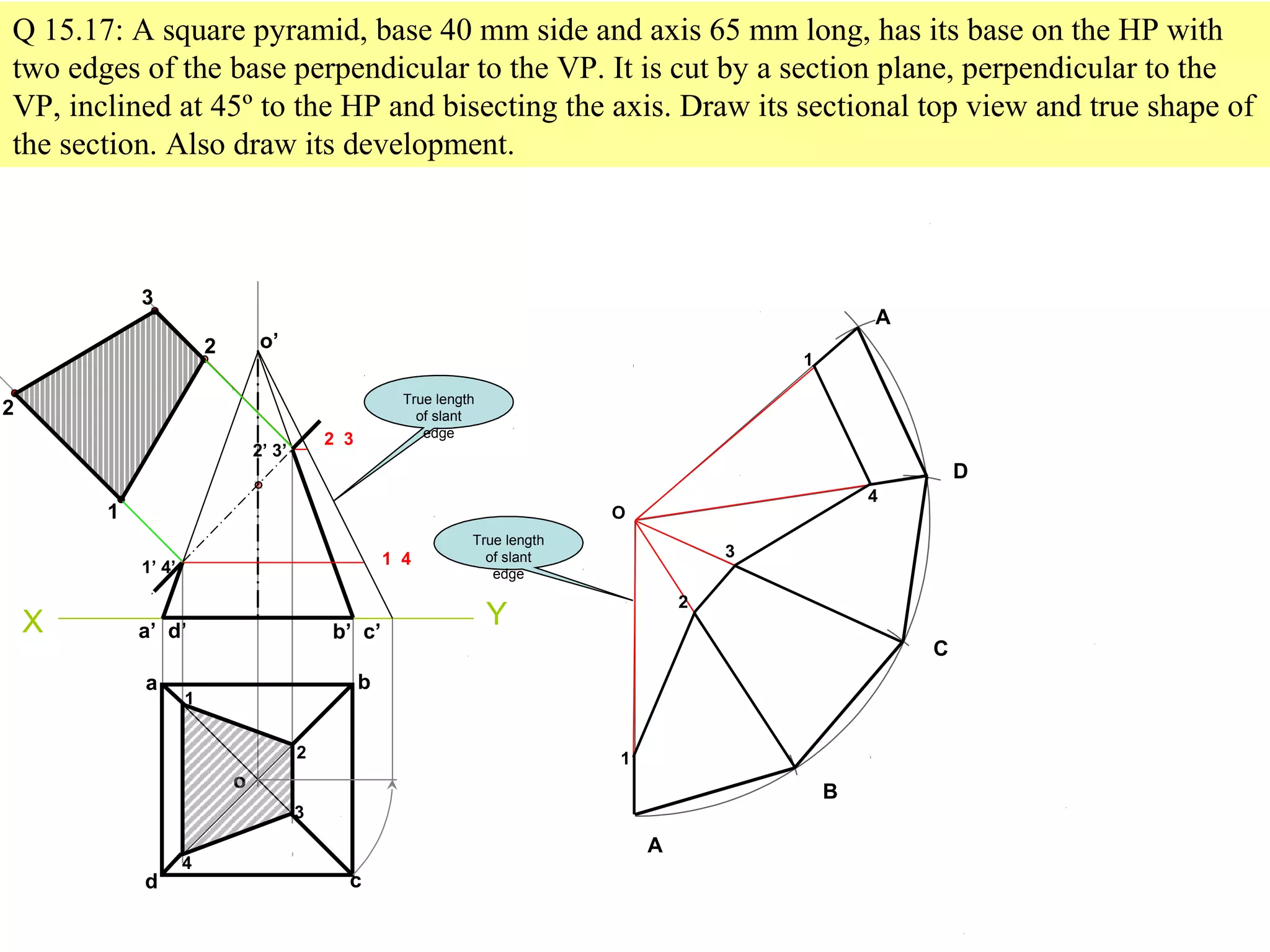
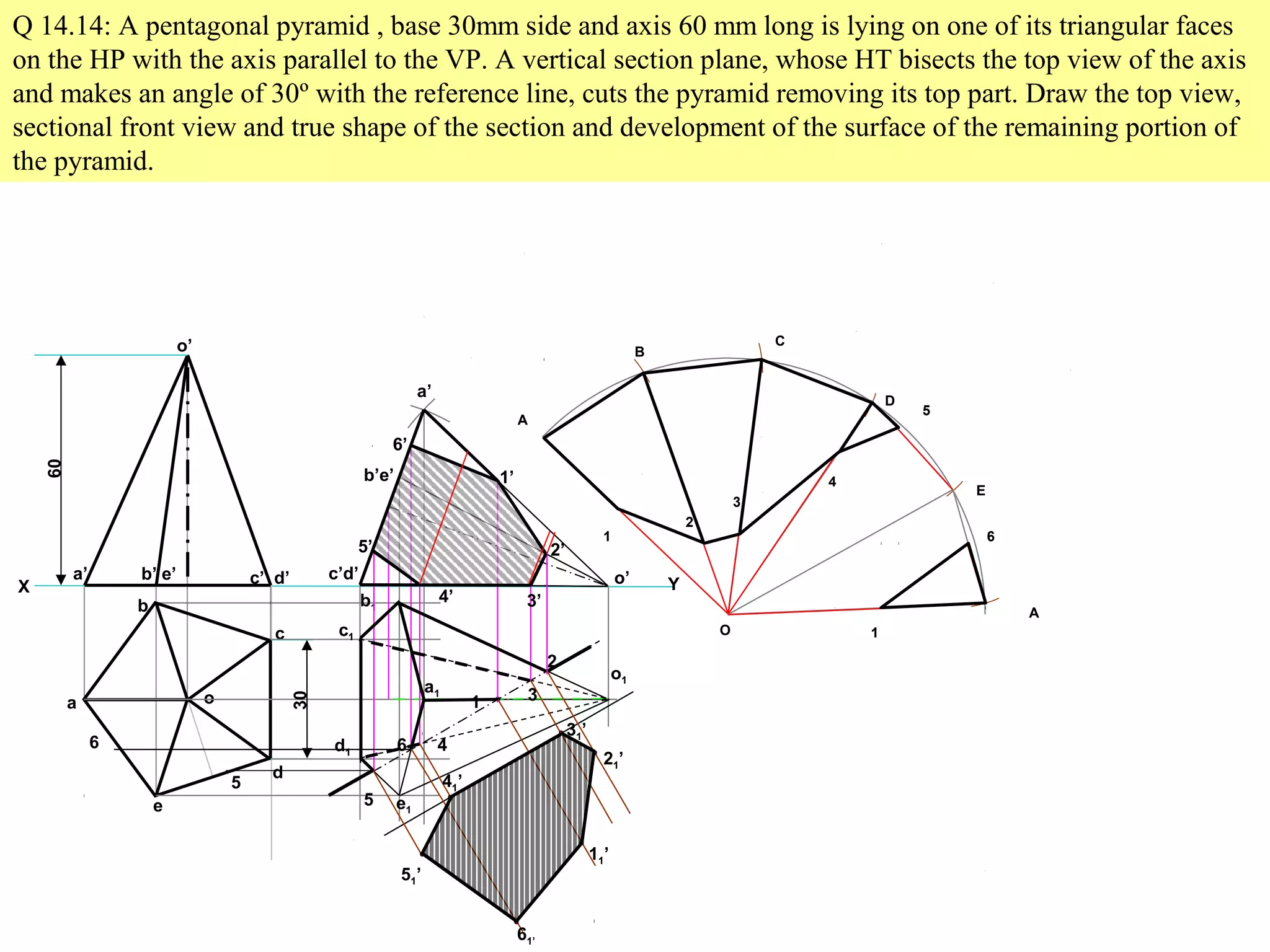
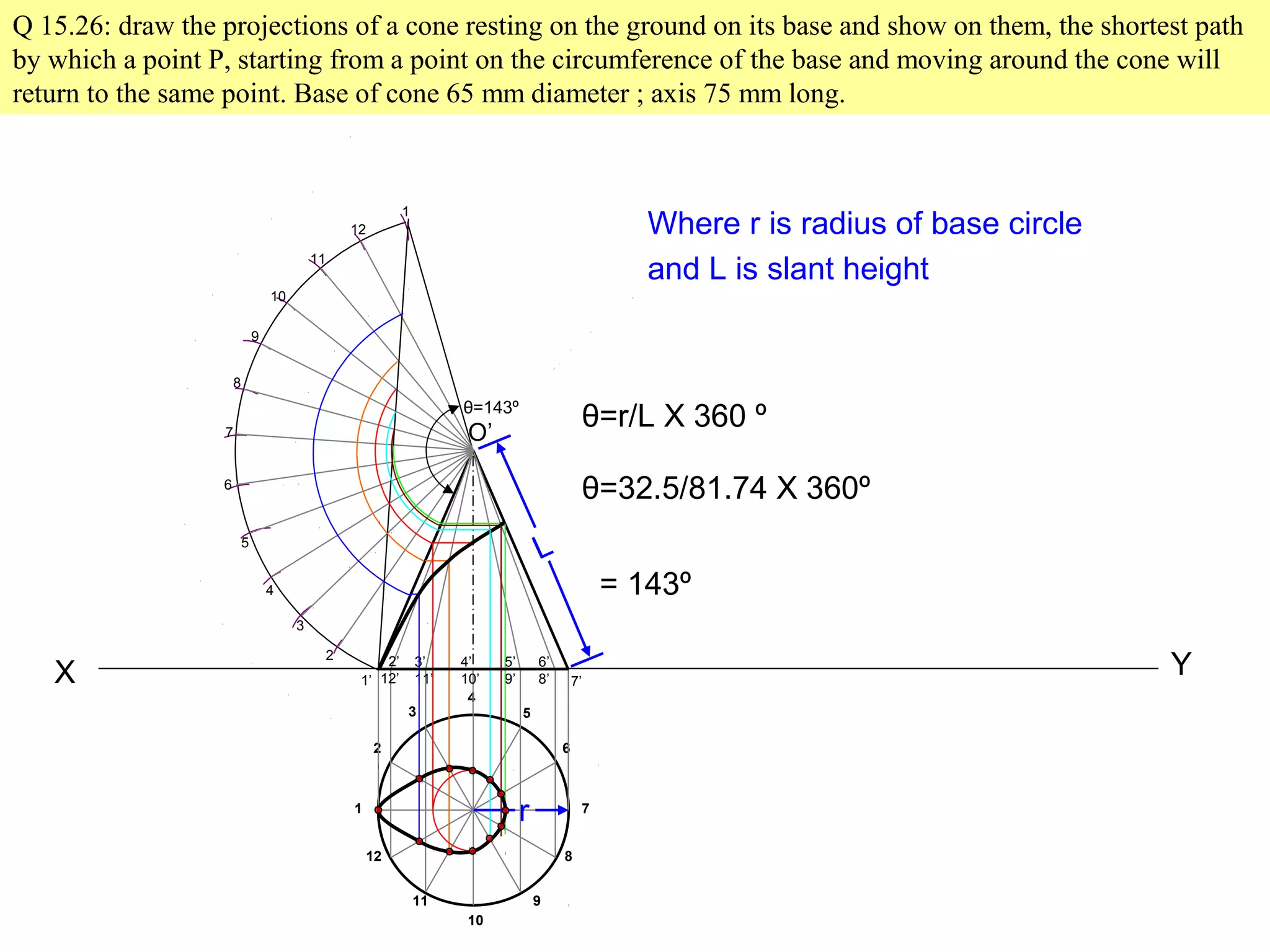
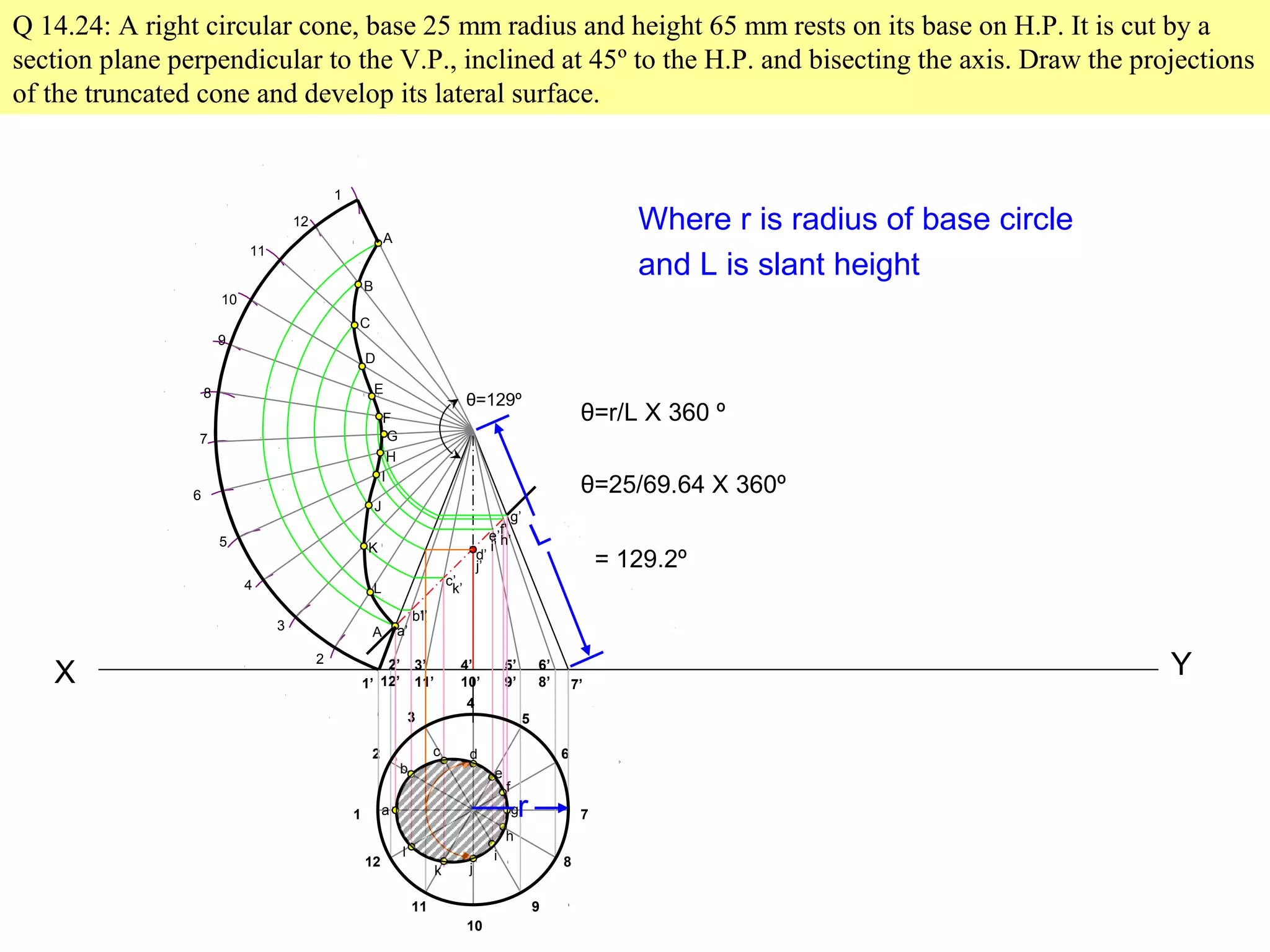
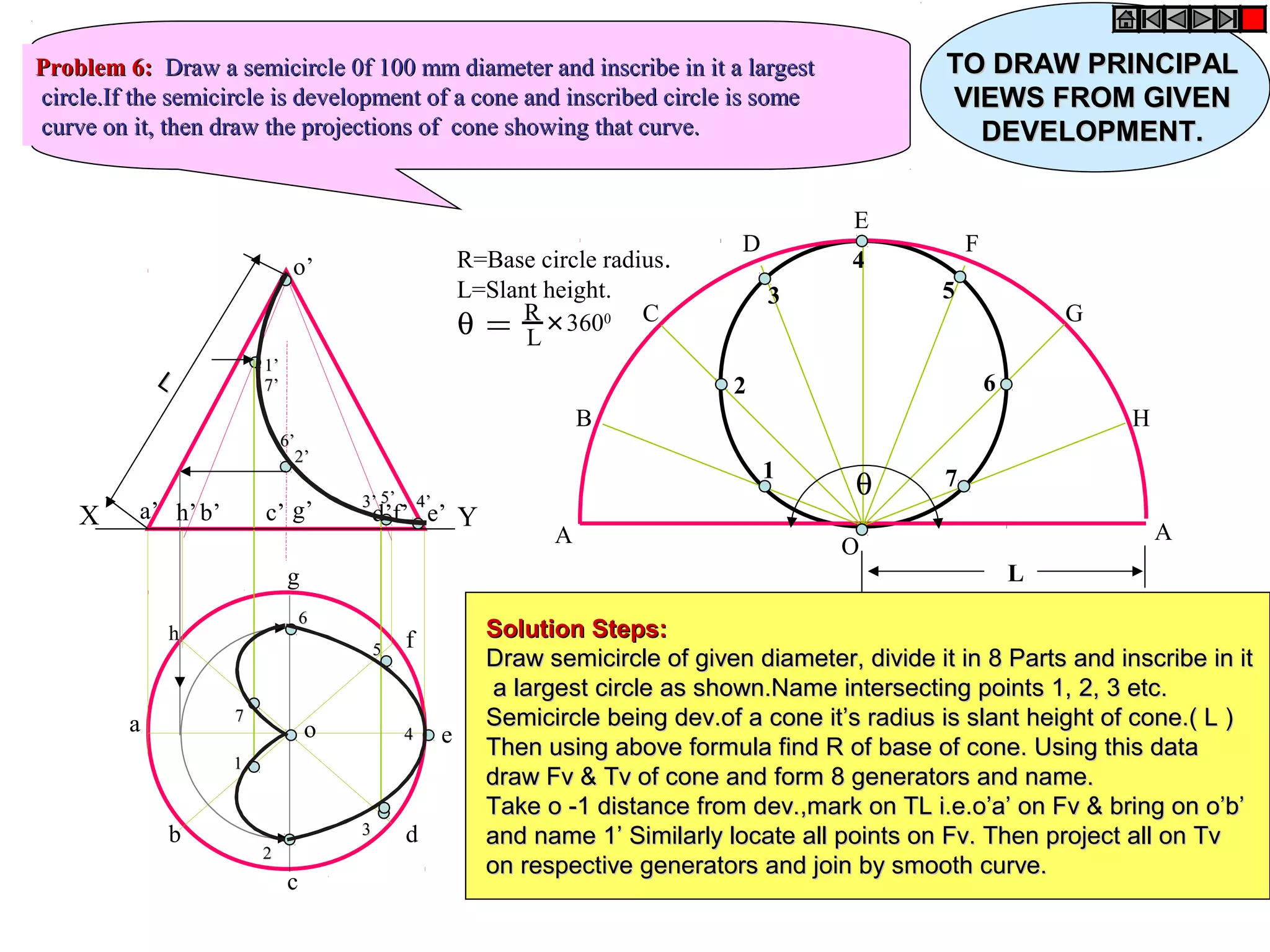
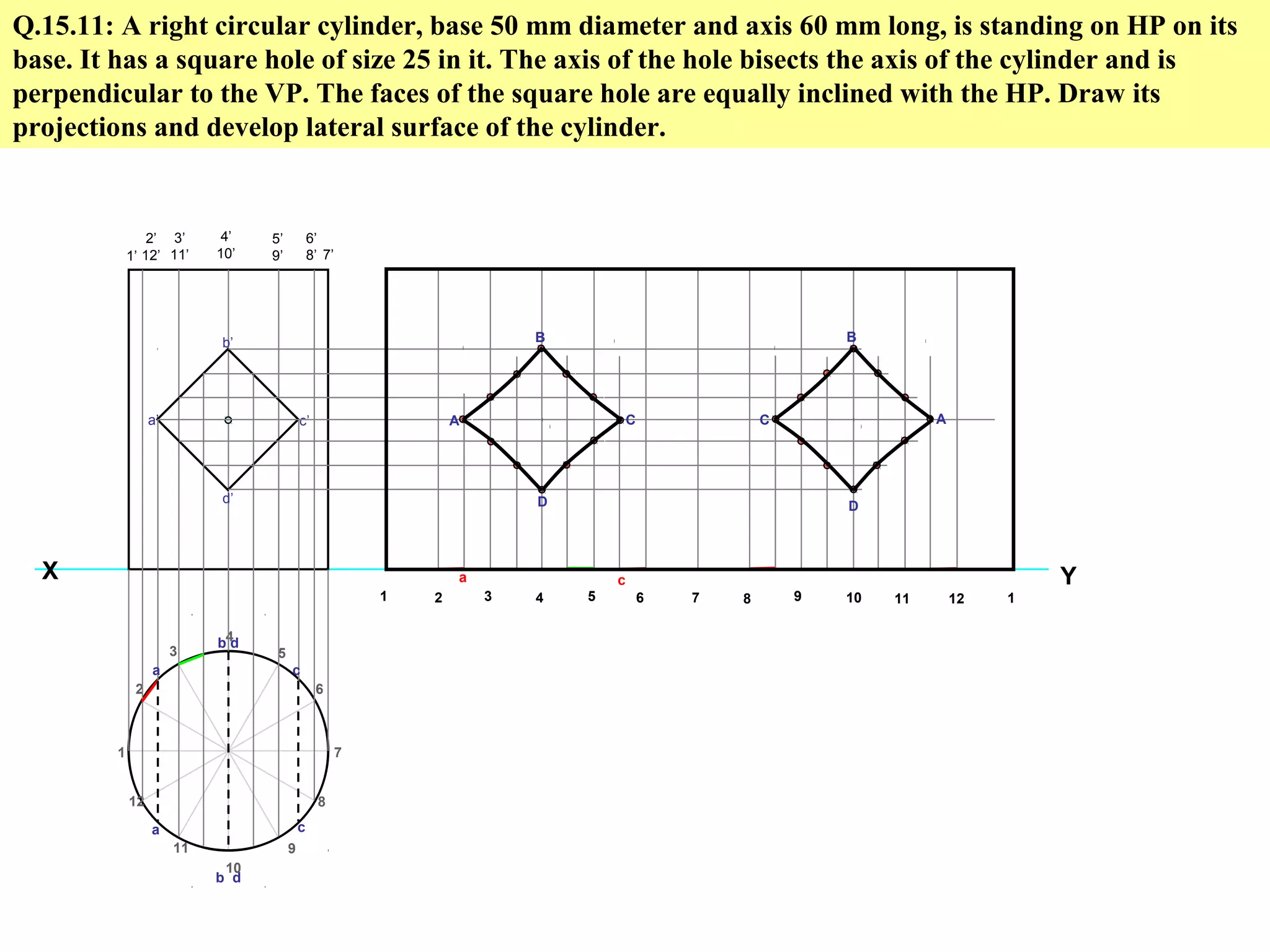
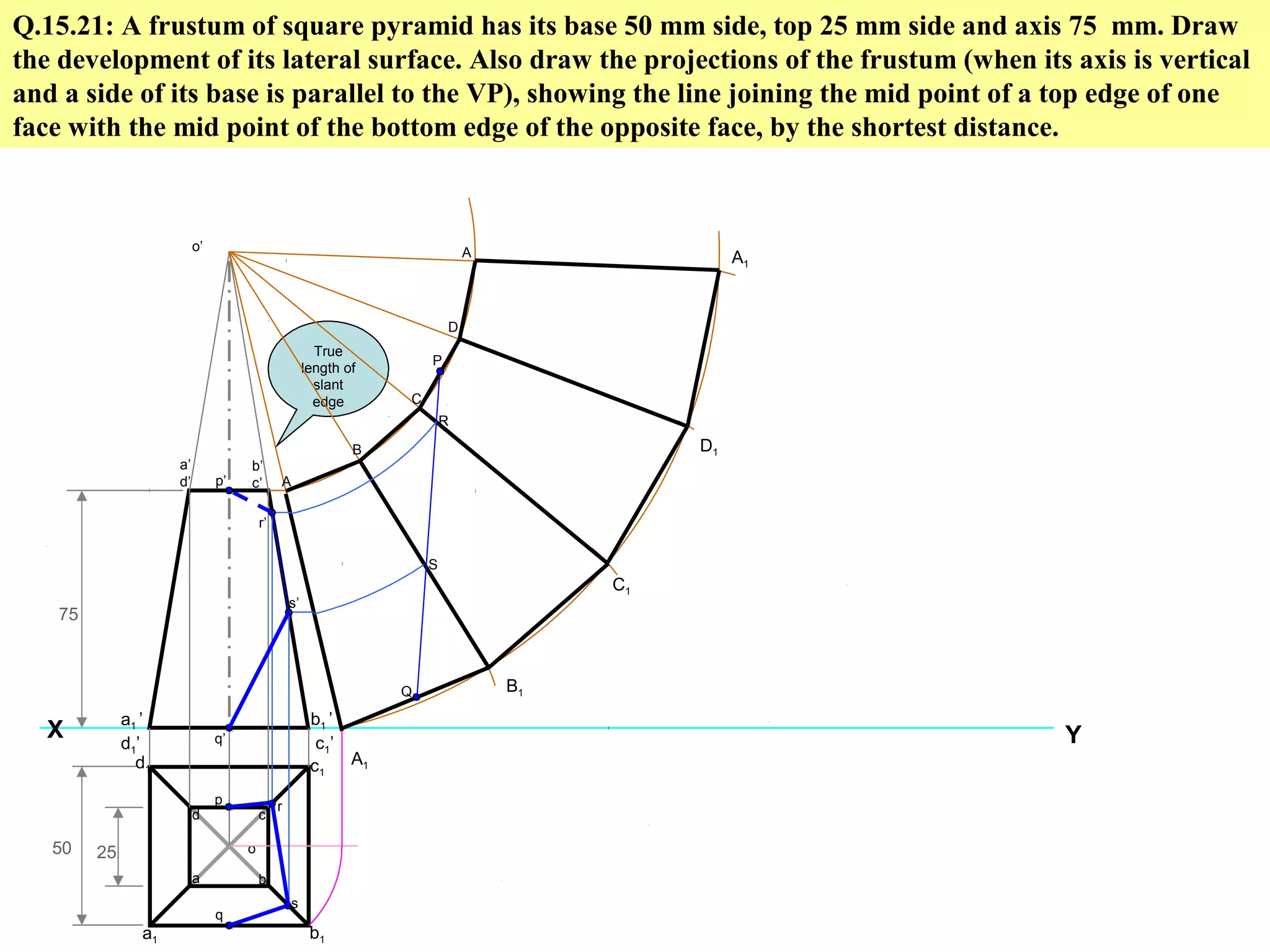
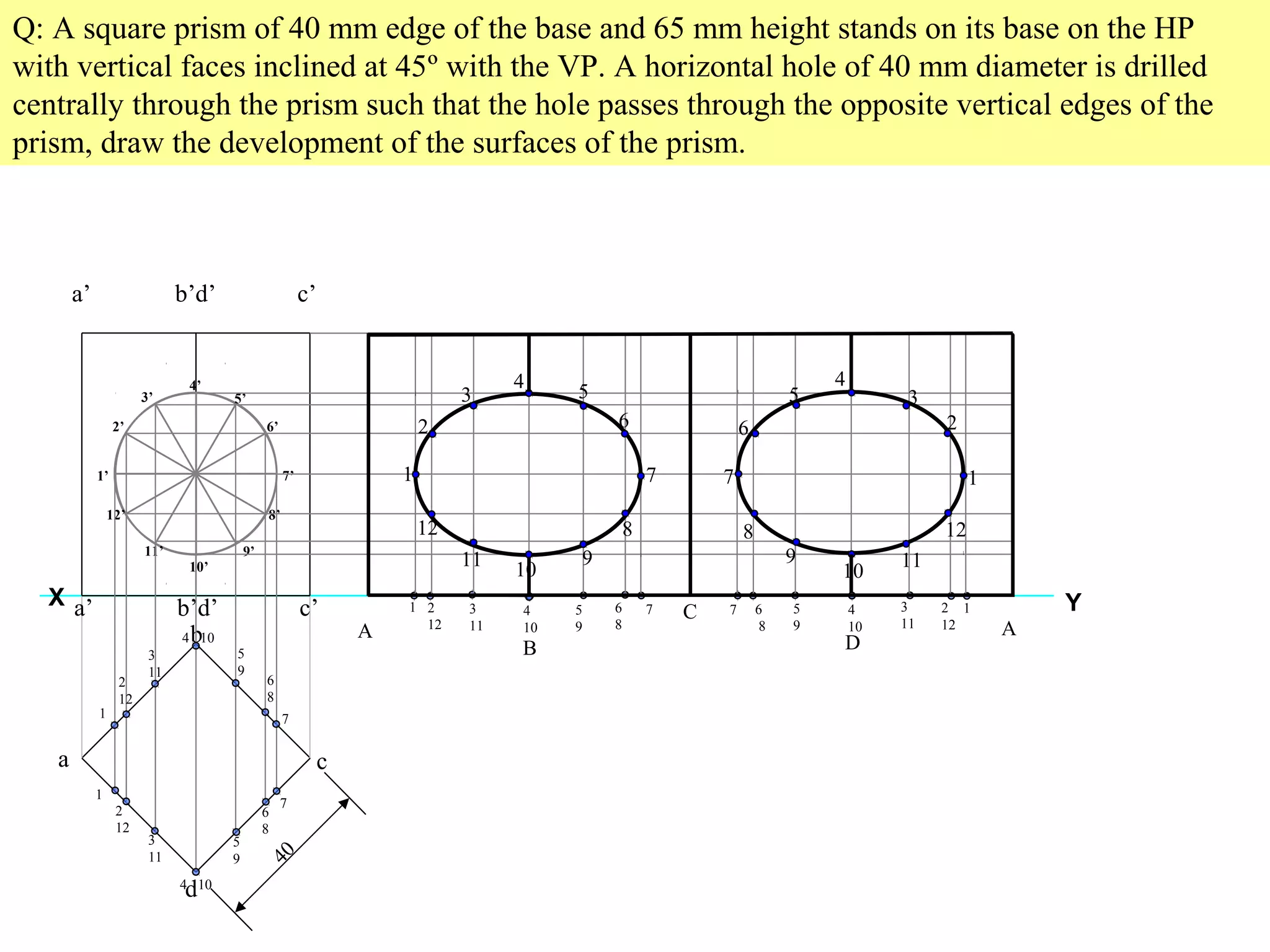
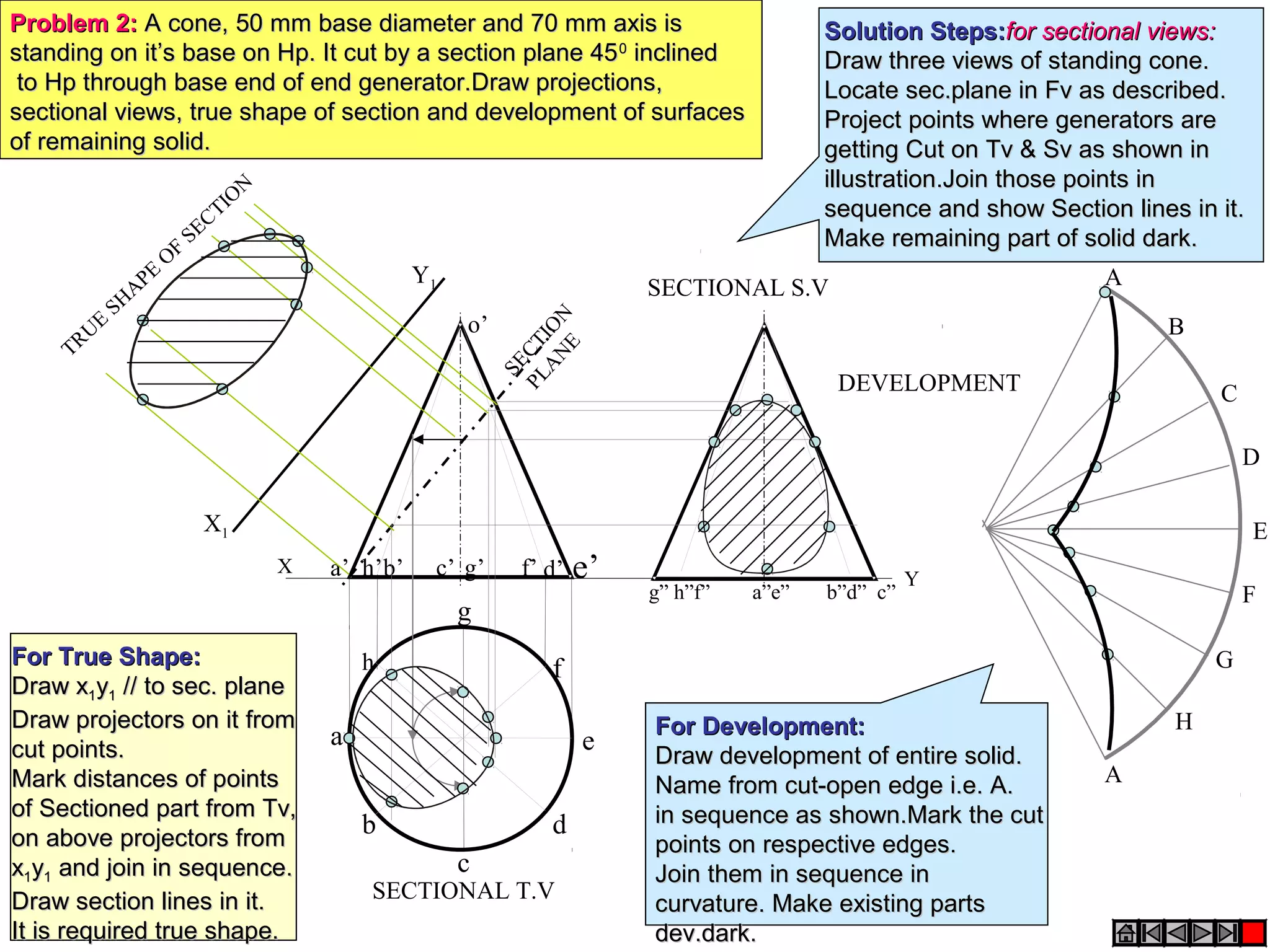
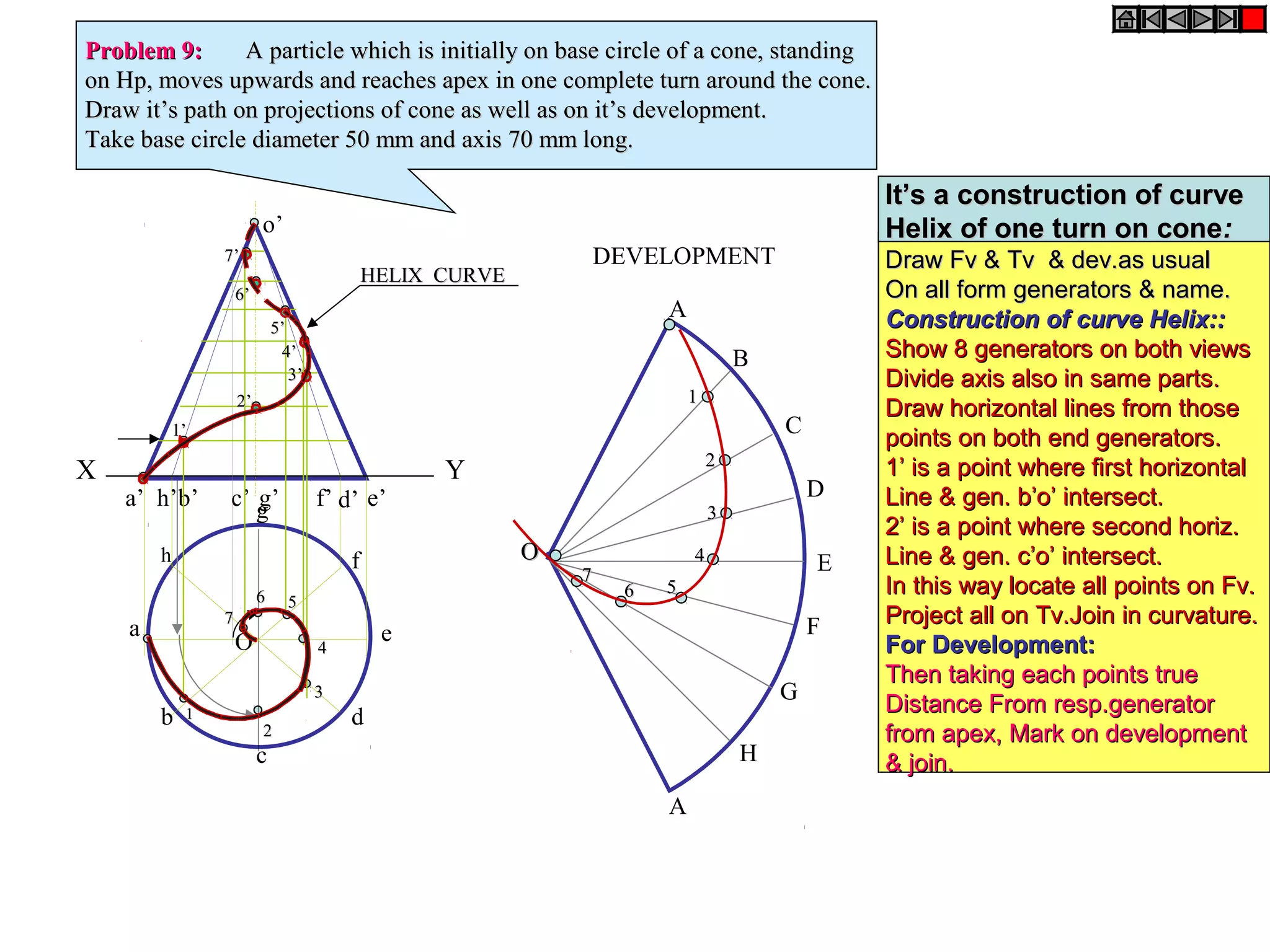
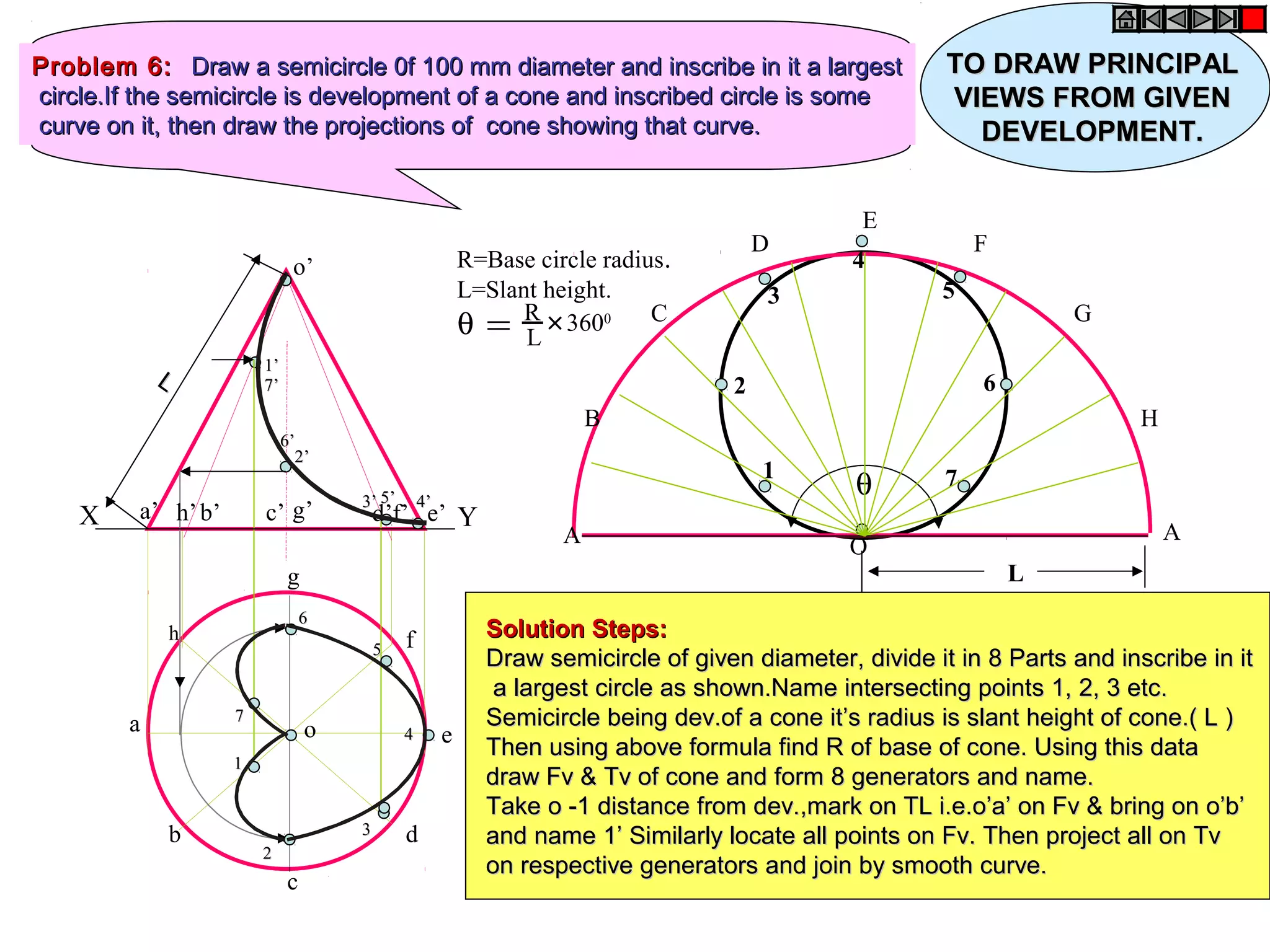
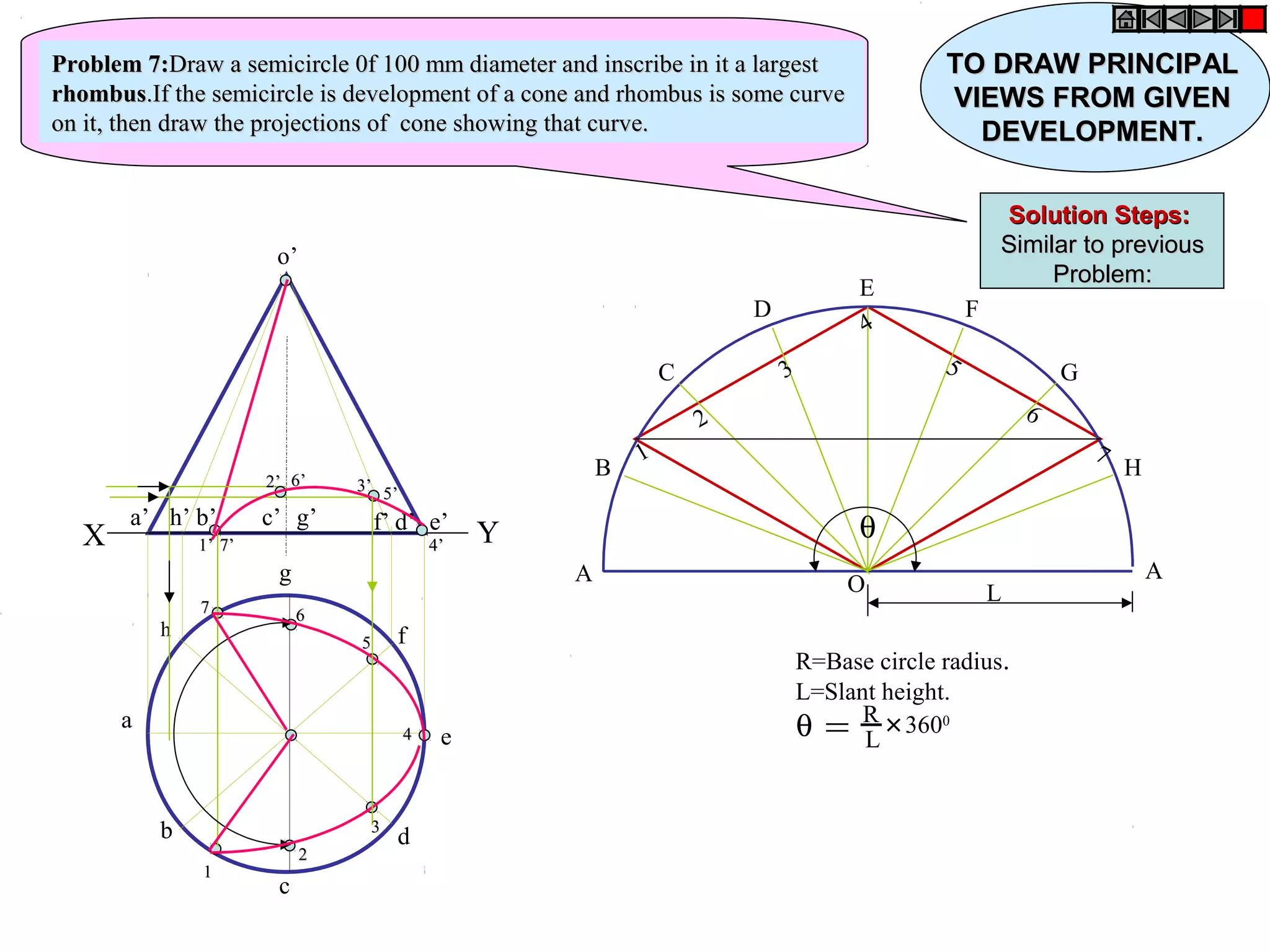
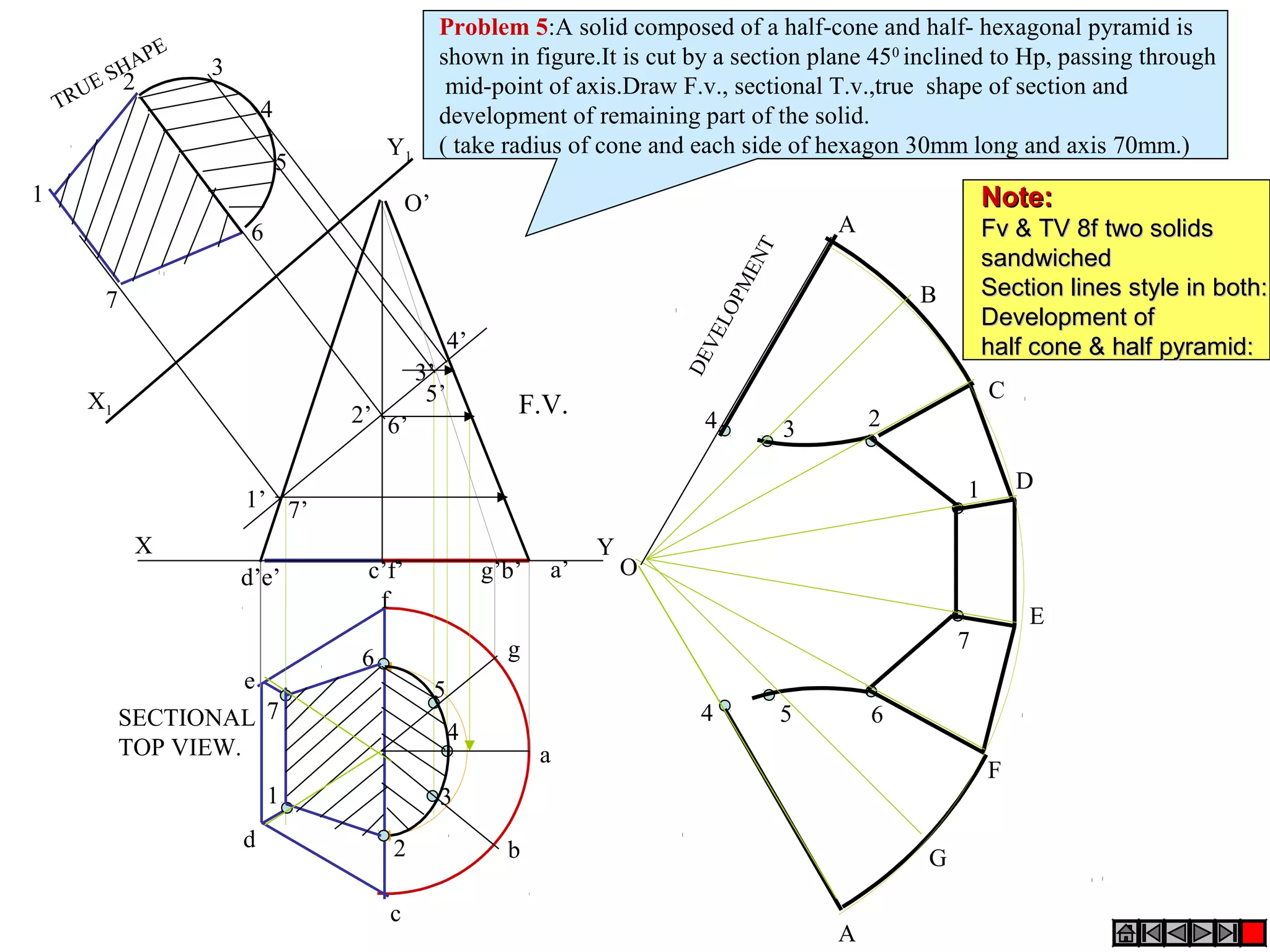
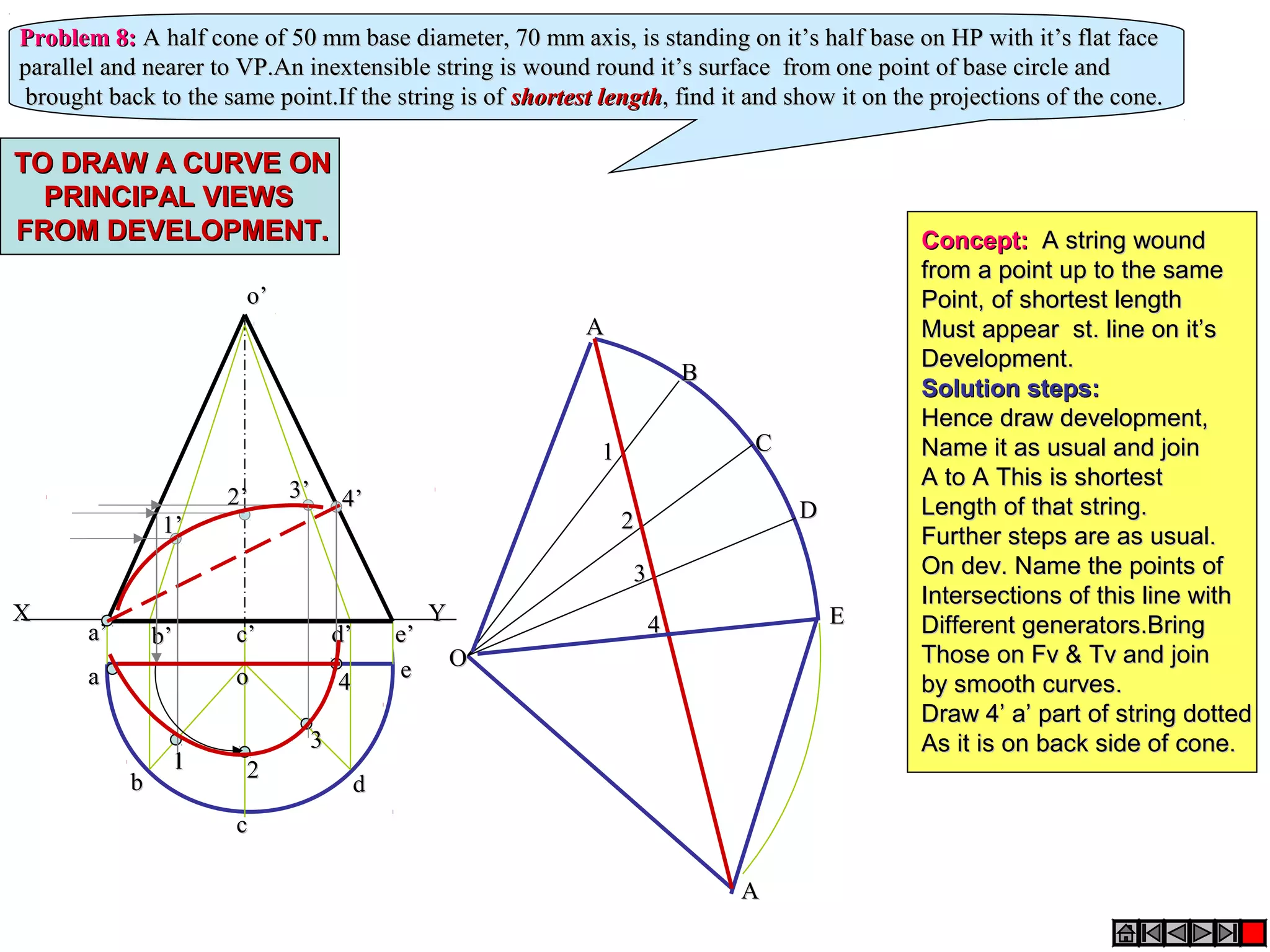
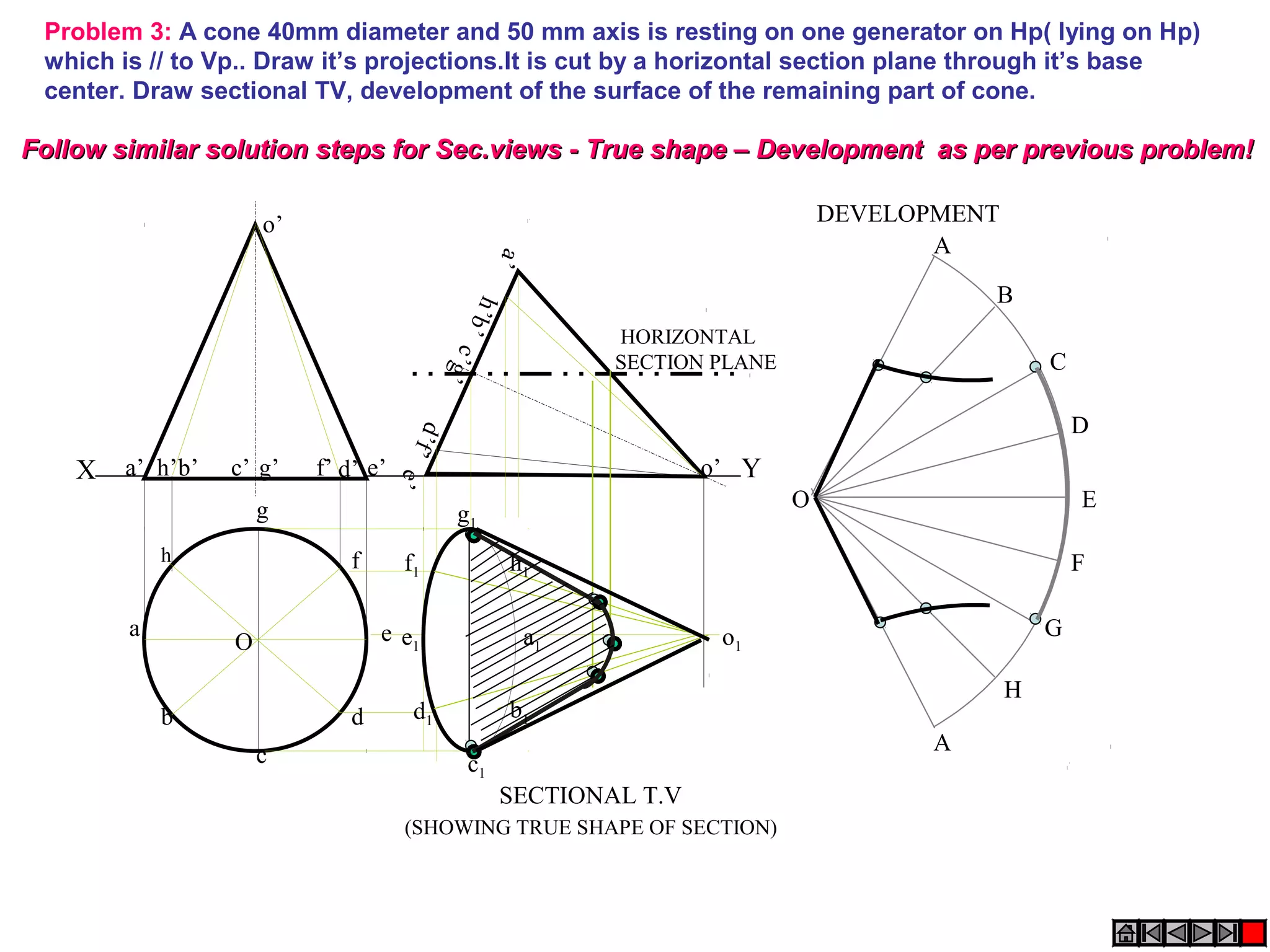
The document discusses sections and developments of solids. It defines sectioning a solid as cutting it with an imaginary cutting plane to understand its internal details. The cutting plane is called the section plane. It shows how to draw the true shape of a section and the development of the remaining solid. It provides examples of typical section planes and shapes formed for different solids. It also defines development as the shape of an unfolded sheet representing the lateral surfaces of a hollow solid. Examples of its engineering applications are given. The document concludes with problems demonstrating how to draw sections, true shapes and developments of various solids.