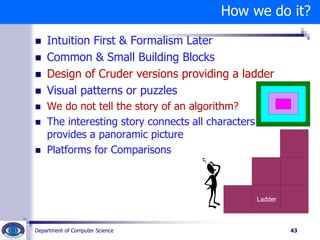
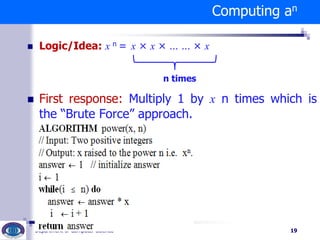
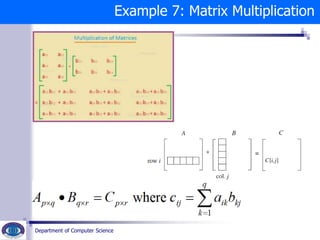
The document discusses the brute force algorithm design technique. It provides examples of problems that can be solved using brute force, including swapping variables, computing powers and factorials, sorting, searching, and matrix multiplication. Brute force involves systematically enumerating all possible candidates for solutions and checking if each candidate satisfies the problem's statement. The document outlines brute force algorithms for several problems and discusses the strengths and weaknesses of the brute force approach.




























![Department of Computer Science
Brute-Force Polynomial Evaluation
Problem: Find the value of polynomial
p(x) = anxn + an-1xn-1 +… + a1x1 + a0
at a point x = x0
Brute-force algorithm
p 0.0
for i n downto 0 do
power 1
for j 1 to i do //compute xi
power power x
p p + a[i] power
return p
Example-9](https://image.slidesharecdn.com/bruteforce1-231226145156-feb7ee7e/85/Design-and-Analysis-of-Algorithm-Brute-Force-1-ppt-32-320.jpg)
![Department of Computer Science
Polynomial Evaluation: Improvement
We can do better by evaluating from right to left:
Better brute-force algorithm
p a[0]
power 1
for i 1 to n do
power power x
p p + a[i] power
return p
Example-9](https://image.slidesharecdn.com/bruteforce1-231226145156-feb7ee7e/85/Design-and-Analysis-of-Algorithm-Brute-Force-1-ppt-33-320.jpg)
![Department of Computer Science
Problem: Design an algorithm convert a 2D array
into 1D array
Solution:
What is input
An 2D-array A[i][j]. e. g. int [5][5]
What should be the output
You could picture the conversion
to the corresponding 1-D array
like this:
Example-10
:](https://image.slidesharecdn.com/bruteforce1-231226145156-feb7ee7e/85/Design-and-Analysis-of-Algorithm-Brute-Force-1-ppt-34-320.jpg)
![Department of Computer Science
Which designing technique?
Brute-Force
Logic/Idea
A 1-D array looks like this:int [5] :
You could picture the conversion to the corresponding 1-D array
like this
Example-10
:](https://image.slidesharecdn.com/bruteforce1-231226145156-feb7ee7e/85/Design-and-Analysis-of-Algorithm-Brute-Force-1-ppt-35-320.jpg)
![Department of Computer Science
Logic/Idea
But an alternative way of thinking about it is to
picture the original array, but re-labelled - like this
Example-10
:
2-D array index [i][j] => 1-D array index [i*5 + j]](https://image.slidesharecdn.com/bruteforce1-231226145156-feb7ee7e/85/Design-and-Analysis-of-Algorithm-Brute-Force-1-ppt-36-320.jpg)
![Department of Computer Science
Example-10
ALGORITHM Convert2d_into_1D(arr2D[i][j], arr1D [n*m])
Input:
OutPut:
for (i = 0; i < n; ++i)
{
for (j = 0; j < m; ++j)
{ // mapping 2D array to 1D array
arr1D[i * m + j] = arr2D[i][j];
}
}
2-D array index [i][j] => 1-D array index [i*5 + j]](https://image.slidesharecdn.com/bruteforce1-231226145156-feb7ee7e/85/Design-and-Analysis-of-Algorithm-Brute-Force-1-ppt-37-320.jpg)