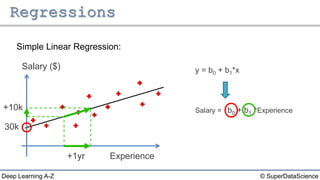
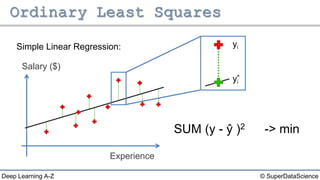
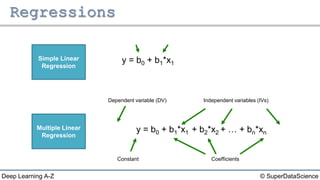
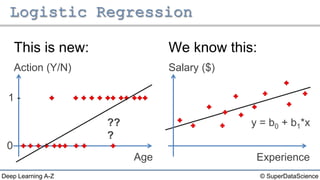
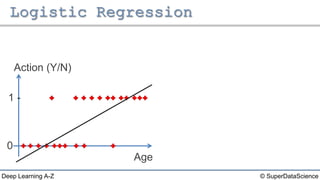
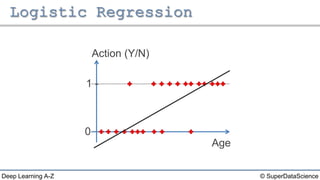
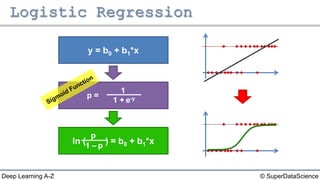
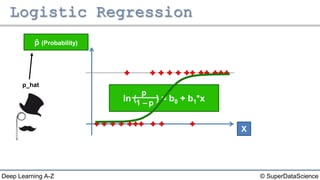
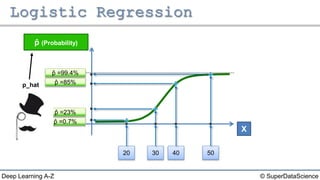
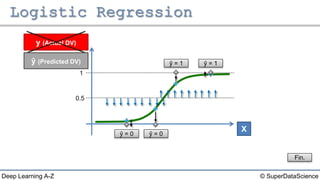
The document discusses different types of regression models: - Simple linear regression predicts a dependent variable from a single independent variable. - Multiple linear regression predicts a dependent variable from multiple independent variables. - Logistic regression predicts a binary dependent variable (e.g. yes/no) from independent variables by modeling the probability.

1. © SuperDataScienceDeep Learning A-Z

2. © SuperDataScienceDeep Learning A-Z

3. © SuperDataScienceDeep Learning A-Z
Simple Linear
Regression
y = b0 + b1*x1
Dependent variable (DV) Independent variable (IV)
CoefficientConstant

4. © SuperDataScienceDeep Learning A-Z
Simple Linear Regression:
Salary ($)
Experience
y = b0 + b1*x
Salary = b0 + b1 *Experience
+1yr
+10k
30k

5. © SuperDataScienceDeep Learning A-Z

6. © SuperDataScienceDeep Learning A-Z
Simple Linear Regression:
Salary ($)
Experience
yî
yi
SUM (y - ŷ )2 -> min

7. © SuperDataScienceDeep Learning A-Z

8. © SuperDataScienceDeep Learning A-Z
Simple Linear
Regression
Multiple Linear
Regression
y = b0 + b1*x1
y = b0 + b1*x1 + b2*x2 + … + bn*xn
Dependent variable (DV) Independent variables (IVs)
Constant Coefficients

9. © SuperDataScienceDeep Learning A-Z

10. © SuperDataScienceDeep Learning A-Z
y = b0 + b1*x1 + … + bn*xn
Linear Regression:
y = b0 + b1*x
- Simple:
- Multiple:

11. © SuperDataScienceDeep Learning A-Z
We know this:This is new:
Salary ($)
Experience
y = b0 + b1*x??
?
Action (Y/N)
Age
0
1 -

12. © SuperDataScienceDeep Learning A-Z
Action (Y/N)
Age
0
1 -

13. © SuperDataScienceDeep Learning A-Z
1 -
Action (Y/N)
Age
0

14. © SuperDataScienceDeep Learning A-Z
1 -
Action (Y/N)
Age
0

15. © SuperDataScienceDeep Learning A-Z
y = b0 + b1*x
1 + e-y
1
p =
ln ( ) = b0 + b1*x1 – p
p

16. © SuperDataScienceDeep Learning A-Z

17. © SuperDataScienceDeep Learning A-Z
ln ( ) = b0 + b1*x1 – p
p
y (Actual DV)
X
p̂ (Probability)
p_hat

18. © SuperDataScienceDeep Learning A-Z
X
p̂ (Probability)
20 30 40 50
p̂ =0.7%
p̂ =23%
p̂ =85%
p̂ =99.4%
p_hat

19. © SuperDataScienceDeep Learning A-Z
X
p̂ (Probability)y (Actual DV)
ŷ (Predicted DV)
0.5
ŷ = 0 ŷ = 0
ŷ = 1 ŷ = 1
1
Fin.