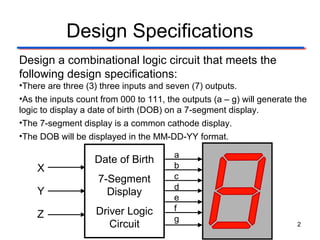
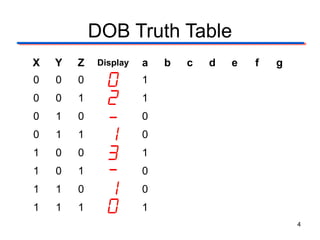
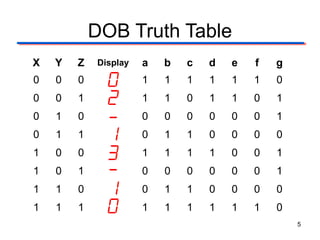
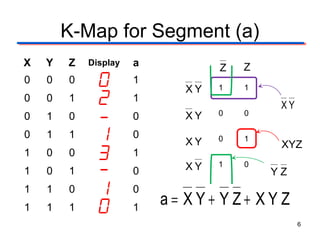
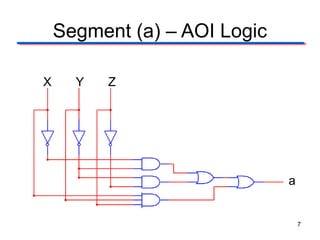
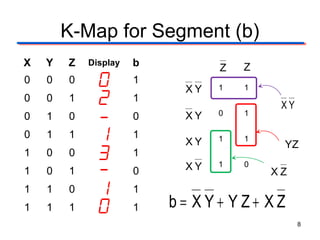
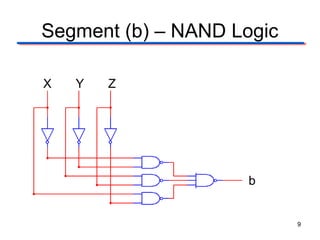
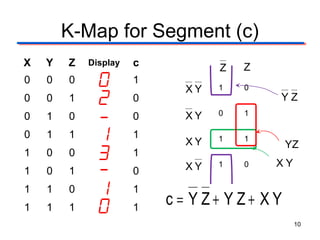
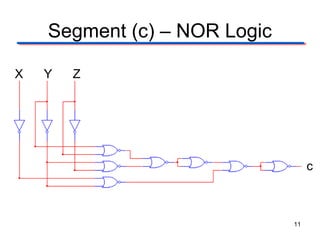
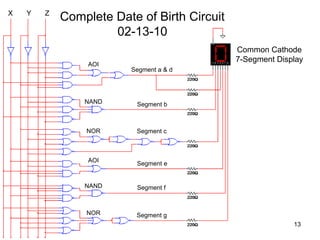
This document describes the design of a combinational logic circuit to display a date of birth on a 7-segment display. The circuit has 3 inputs (X, Y, Z) that will cycle through binary codes to represent dates. It drives 7 outputs (a-g) to control the display segments. Truth tables and K-maps are used to derive the logic expressions for each segment. The final circuit uses AOI, NAND and NOR gates to generate the correct segment outputs from the 3 inputs to display the date 02-13-10.