Recommended
PPTX
Τα οικόσημα - Μέρος 2.pptx
DOCX
PDF
PPT
PPTX
PDF
PDF
PPT
DOCX
Φύλλο εργασίας Ιουδαϊσμός.docx
PPTX
PDF
ระดับของสมรรถนะหลักของข้าราชการกรุงเทพมหานคร
PPT
การวิเคราะห์อัลกอริทึม(algorithm analysis)
DOC
أسئلة اختبارات اللغة الإنجليزية لمسابقة المعلمين
PPT
PDF
ชุดฝึกทักษะกีฬาเรื่องการยิงประตูและการป้องกันประตูกีฬาแฮนด์บอล
PDF
PPT
PPSX
علامات الاسم والفعل والحرف
PDF
PPTX
1.5α Η ΣΧΕΣΗ ΜΑΣ ΜΕ ΤΟΝ ΘΕΟ
PDF
PDF
DOCX
PPTX
1-9.Χριστούγεννα με κείμενα (2022)
PDF
เอกสารประกอบการสอน เล่มที่ 7 เรื่อง การตรวจสอบและแก้ไขข้อขัดข้องระบบไฟฟ้าในบ้าน
PDF
ข้อสอบศลปะ ป.6 ภูมิปัญญาทางดนตรี
PPT
DOCX
แบบสำรวจรายการแข่งทักษะวิชาการ
PPT
dokumen.tips_binary-search-tree-5698bcbd37e20.ppt
PPT
More Related Content
PPTX
Τα οικόσημα - Μέρος 2.pptx
DOCX
PDF
PPT
PPTX
PDF
PDF
PPT
What's hot
DOCX
Φύλλο εργασίας Ιουδαϊσμός.docx
PPTX
PDF
ระดับของสมรรถนะหลักของข้าราชการกรุงเทพมหานคร
PPT
การวิเคราะห์อัลกอริทึม(algorithm analysis)
DOC
أسئلة اختبارات اللغة الإنجليزية لمسابقة المعلمين
PPT
PDF
ชุดฝึกทักษะกีฬาเรื่องการยิงประตูและการป้องกันประตูกีฬาแฮนด์บอล
PDF
PPT
PPSX
علامات الاسم والفعل والحرف
PDF
PPTX
1.5α Η ΣΧΕΣΗ ΜΑΣ ΜΕ ΤΟΝ ΘΕΟ
PDF
PDF
DOCX
PPTX
1-9.Χριστούγεννα με κείμενα (2022)
PDF
เอกสารประกอบการสอน เล่มที่ 7 เรื่อง การตรวจสอบและแก้ไขข้อขัดข้องระบบไฟฟ้าในบ้าน
PDF
ข้อสอบศลปะ ป.6 ภูมิปัญญาทางดนตรี
PPT
DOCX
แบบสำรวจรายการแข่งทักษะวิชาการ
Similar to avl tree ,b-tree
PPT
dokumen.tips_binary-search-tree-5698bcbd37e20.ppt
PPT
PPTX
PPT
PPT
PPT
More from tumetr
DOCX
ขั้นตอนการสร้าง Facebook page
PPTX
ตั้งรับ ขับเคลื่อนธุรกิจและผลักดันคนไอทีไทยสู่-Aec-2015
PPTX
PPTX
PPT
The system-analysis-and-design
PPT
การพัฒนาและติดตั้งระบบ(System implementation)
PPT
PPT
ส่วนจัดการสื่อประสานผู้ใช้(User interface-management)
PPT
PPT
An approach-to-planning-software-projects
PPT
PPT
PPTX
ทรัพยากรมนุษย์และการออกแบบงาน
PPTX
กลยุทธ์การเลือกทำเลที่ตั้งสถานประกอบการ
PPT
กลยุทธ์การวางผังสถานประกอบการ
PDF
หน่วยที่ 5.3.2 การสุขาภิบาลอาหาร
PDF
หน่วยที่ 5.3.1 สารปนเปื้อนในอาหาร
PDF
หน่วยที่ 5.2 ผลิตภัณฑ์อาหารเพื่อสุขภาพ
PPT
โครงสร้างข้อมูลแบบลิงค์ลิสต์ (linklist)
PPT
การจัดเรียงข้อมูล (sorting)
avl tree ,b-tree 1. 2. AVL Tree (Adelson-Velskii and
Landis Tree)
นิยามของ AVL Tree
1. เป็น binary search tree
2. เป็น Balanced tree
Balanced tree หมายถึง Tree ที่มีคุณสมบัติ
ดังนี้คือ ทุกโหนดใน tree ต้องมีค่านำ้าหนักประจำา
โหนด เป็น -1 , 0 หรือ 1 เท่านั้น
นำ้าหนักของโหนด R = ความสูงของ TL - ความสูง
ของ TR
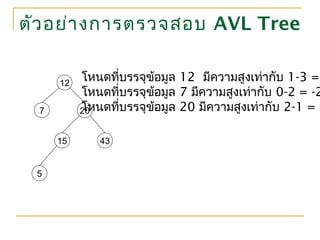
3. ตัวอย่างการตรวจสอบ AVL Tree
5
12
7 20
15 43
โหนดที่บรรจุข้อมูล 12 มีความสูงเท่ากับ 1-3 =
โหนดที่บรรจุข้อมูล 7 มีความสูงเท่ากับ 0-2 = -2
โหนดที่บรรจุข้อมูล 20 มีความสูงเท่ากับ 2-1 = 1
4. 5. 6. 2. Right of Right
เกิดเมื่อมีการแทรกโหนดเข้าไปด้าน sub-tree ฝั่ง
ขวาของโหนดลูกทางขวา
15
11
5 24
45 15
11
5 24
45
82
เกิด Imbalance
เดิมต้นไม้สมดุลย์ ต้นไม้ไม่สมดุลย์
7. 8. 4. Left of Right
มื่อมีการแทรกโหนดเข้าไปด้าน sub-tree ฝั่งขวาของโหนดลูกทา
15
11
5 24
45 15
11
5 24
45
18
เกิด Imbalance
9. การทำา Balancing Tree
1. Single rotation
การหมุน 1 ครั้ง ใช้กรณีเกิด Left of Left
และ Right of Right
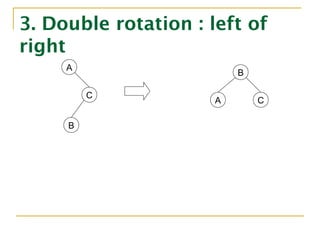
2. Double rotation
การหมุน 2 ครั้ง ใช้กรณีเกิด Right of Left
และ Left of Right
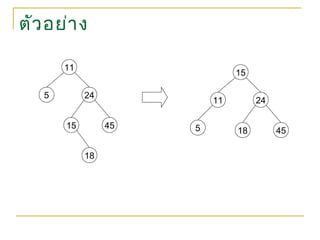
10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. ตัวอย่าง
ร้าง AVL Tree จากข้อมูลที่นำาเข้ามาตามลำาดับดังต่อไปน
23, 54, 34, 2, 14, 7, 26, 16, 87, 21, 9
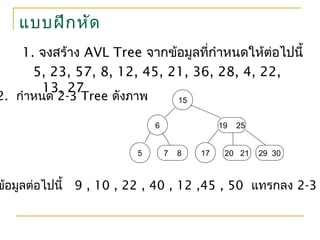
21. 22. 23. 24. แบบฝึกหัด
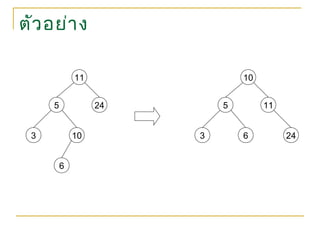
1. จงสร้าง AVL Tree จากข้อมูลที่กำาหนดให้ต่อไปนี้
5, 23, 57, 8, 12, 45, 21, 36, 28, 4, 22,
13, 27
2. กำาหนด 2-3 Tree ดังภาพ 15
19 256
5 7 8 17 20 21 29 30
ข้อมูลต่อไปนี้ 9 , 10 , 22 , 40 , 12 ,45 , 50 แทรกลง 2-3