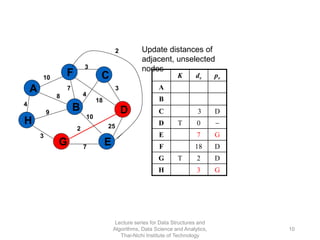
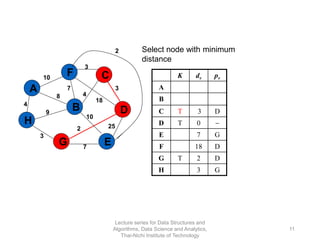
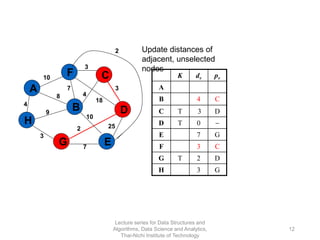
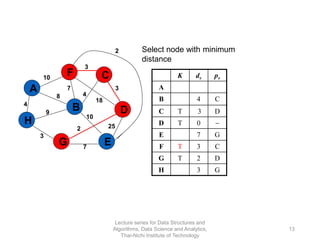
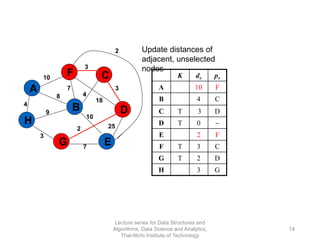
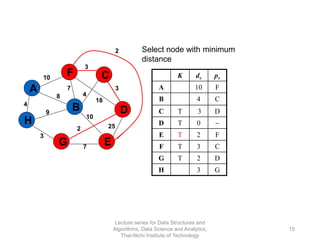
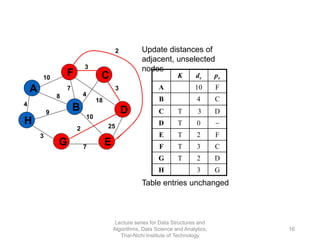
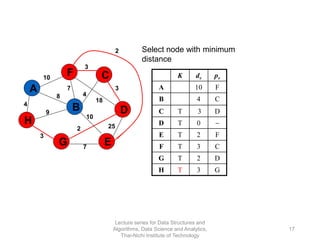
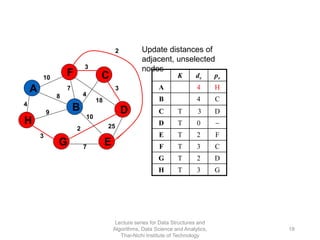
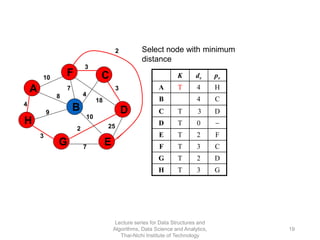
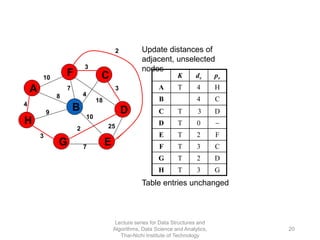
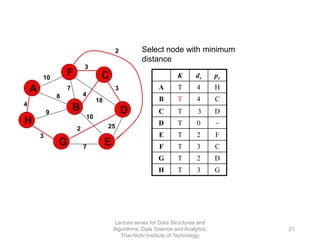
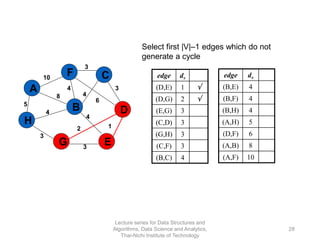
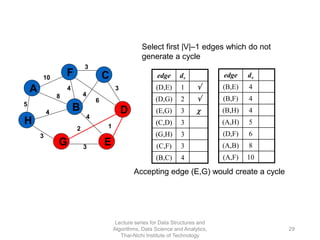
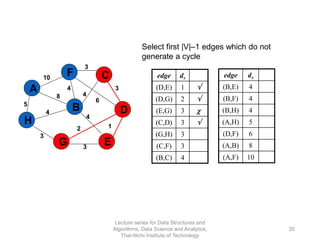
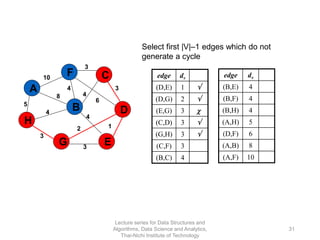
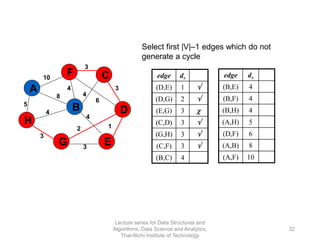
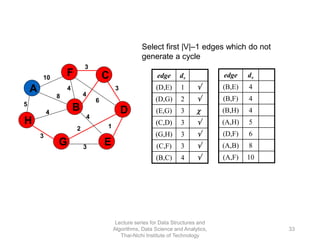
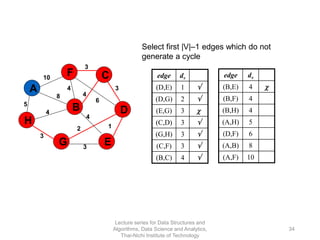
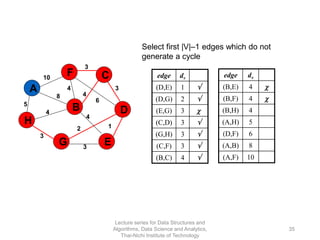
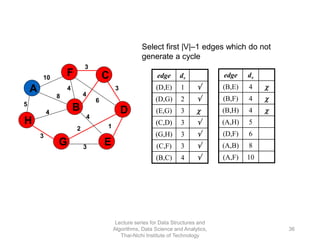
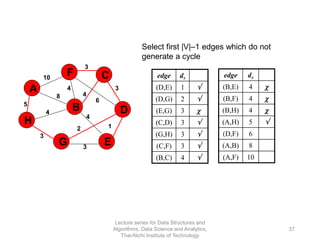
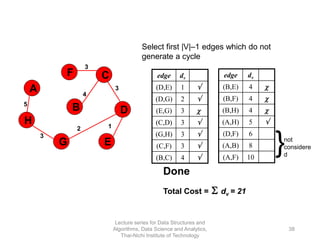
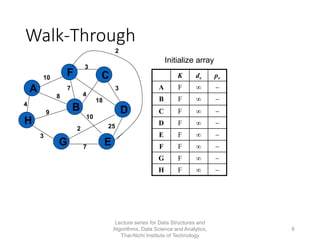
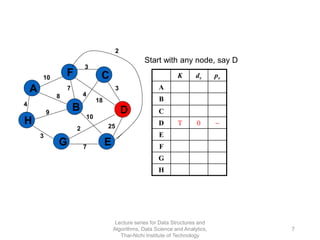
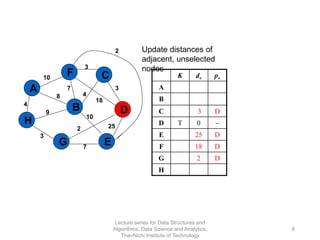
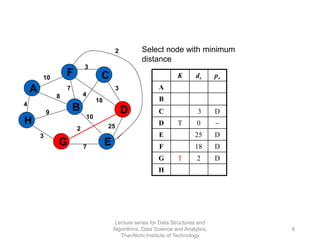
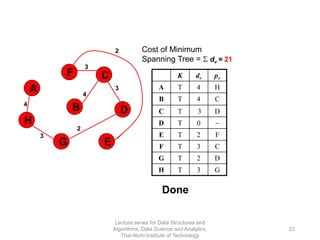
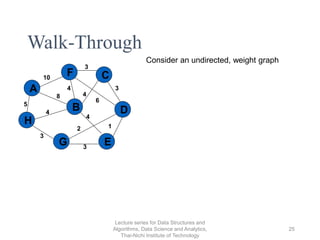
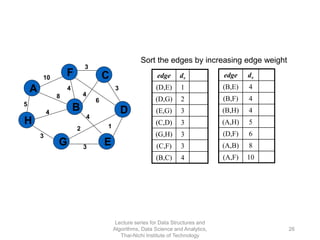
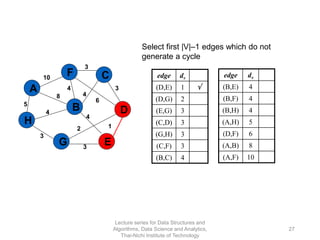
The document discusses minimum spanning trees and provides examples of Prim's and Kruskal's algorithms. It includes: - A definition of minimum spanning tree as a subgraph that spans all nodes with minimum total edge weight. - Characteristics of Prim's and Kruskal's algorithms such as working with undirected, weighted/unweighted graphs and producing optimal solutions greedily. - A walk-through example of Prim's algorithm on a graph and calculating the minimum spanning tree cost.

1. Data Structures and
Algorithms
Week 8: Minimum Spanning Trees
Ferdin Joe John Joseph, PhD
Faculty of Information Technology
Thai-Nichi Institute of Technology, Bangkok

2. Week 8
• Minimum Spanning Trees
• Implementation in Java
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
2

3. Definition
• A Minimum Spanning Tree (MST) is a subgraph of
an undirected graph such that the subgraph spans
(includes) all nodes, is connected, is acyclic, and
has minimum total edge weight
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
3

4. Algorithm Characteristics
• Both Prim’s and Kruskal’s Algorithms work with
undirected graphs
• Both work with weighted and unweighted graphs but
are more interesting when edges are weighted
• Both are greedy algorithms that produce optimal
solutions
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
4

5. Prim’s Algorithm
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
5

6. Walk-Through
Initialize array
K dv pv
A F ∞ −
B F ∞ −
C F ∞ −
D F ∞ −
E F ∞ −
F F ∞ −
G F ∞ −
H F ∞ −
4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
6

7. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Start with any node, say D
K dv pv
A
B
C
D T 0 −
E
F
G
H
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
7

8. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A
B
C 3 D
D T 0 −
E 25 D
F 18 D
G 2 D
H
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
8

9. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A
B
C 3 D
D T 0 −
E 25 D
F 18 D
G T 2 D
H
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
9

10. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A
B
C 3 D
D T 0 −
E 7 G
F 18 D
G T 2 D
H 3 G
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
10

11. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A
B
C T 3 D
D T 0 −
E 7 G
F 18 D
G T 2 D
H 3 G
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
11

12. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A
B 4 C
C T 3 D
D T 0 −
E 7 G
F 3 C
G T 2 D
H 3 G
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
12

13. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A
B 4 C
C T 3 D
D T 0 −
E 7 G
F T 3 C
G T 2 D
H 3 G
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
13

14. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 −
E 2 F
F T 3 C
G T 2 D
H 3 G
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
14

15. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H 3 G
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
15

16. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H 3 G
2
Table entries unchanged
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
16

17. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A 10 F
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
17

18. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A 4 H
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
18

19. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A T 4 H
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
19

20. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Update distances of
adjacent, unselected
nodes
K dv pv
A T 4 H
B 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2
Table entries unchanged
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
20

21. 4
25
A
H
B
F
E
D
C
G 7
2
10
18
3
4
3
7
8
9
3
10
Select node with minimum
distance
K dv pv
A T 4 H
B T 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
21

22. 4
A
H
B
F
E
D
C
G
2
3
4
3
3
Cost of Minimum
Spanning Tree = Σ dv = 21
K dv pv
A T 4 H
B T 4 C
C T 3 D
D T 0 −
E T 2 F
F T 3 C
G T 2 D
H T 3 G
2
Done
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
22

23. Java Implementation
https://www.geeksforgeeks.org/prims-minimum-
spanning-tree-mst-greedy-algo-5/
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
23

24. Kruskal’s Algorithm
Work with edges, rather than nodes
Two steps:
– Sort edges by increasing edge weight
– Select the first |V| – 1 edges that do not
generate a cycle
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
24

25. Walk-Through
Consider an undirected, weight graph
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
25

26. Sort the edges by increasing edge weight
edge dv
(D,E) 1
(D,G) 2
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
26

27. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
27

28. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
28

29. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Accepting edge (E,G) would create a cycle
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
29

30. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
30

31. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
31

32. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
32

33. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
33

34. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 χ
(B,F) 4
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
34

35. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 χ
(B,F) 4 χ
(B,H) 4
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
35

36. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 χ
(B,F) 4 χ
(B,H) 4 χ
(A,H) 5
(D,F) 6
(A,B) 8
(A,F) 10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
36

37. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G 3
2
4
6
3
4
3
4
8
4
3
10 edge dv
(B,E) 4 χ
(B,F) 4 χ
(B,H) 4 χ
(A,H) 5 √
(D,F) 6
(A,B) 8
(A,F) 10
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
37

38. Select first |V|–1 edges which do not
generate a cycle
edge dv
(D,E) 1 √
(D,G) 2 √
(E,G) 3 χ
(C,D) 3 √
(G,H) 3 √
(C,F) 3 √
(B,C) 4 √
5
1
A
H
B
F
E
D
C
G
2
3
3
3
edge dv
(B,E) 4 χ
(B,F) 4 χ
(B,H) 4 χ
(A,H) 5 √
(D,F) 6
(A,B) 8
(A,F) 10
Done
Total Cost = Σ dv = 21
4
}not
considere
d
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
38

39. Java Implementation
https://www.geeksforgeeks.org/kruskals-minimum-
spanning-tree-algorithm-greedy-algo-2/
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
39

40. Next Week
Search Algorithms
Lecture series for Data Structures and
Algorithms, Data Science and Analytics,
Thai-Nichi Institute of Technology
40