This document describes research on efficient data structures and algorithms for solving range aggregate problems. It begins with introductions to computational geometry and classic problems in the field like finding the closest pair of points. It then discusses concepts like output sensitivity and different computation models. Range searching data structures like range trees are described for solving problems like orthogonal range queries. The document outlines solving problems related to planar range maxima and planar range convex hull queries. It proposes preprocessing point data to speed up queries for problems like reporting the skyline points within a 2-sided range.






![Introduction
Background Knowledge
Problems Solved
Conclusion and Future Work
Output Sensitvity
Computation Models
Range Search
Orthogonal Range Successor Queries
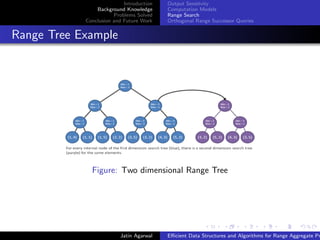
Example
Given an unsorted array of n numbers and any given query
q = [a, b] report all the numbers x in range a < x < b.
5 9 3 1 7 6 4 12 2
Figure: Unsorted Array of Numbers
Jatin Agarwal Efficient Data Structures and Algorithms for Range Aggregate Pr](https://image.slidesharecdn.com/defence-160706143708/85/MS-Thesis-7-320.jpg)






















![Introduction
Background Knowledge
Problems Solved
Conclusion and Future Work
Planar Range Maxima
Planar Range Convex Hull and Related problems
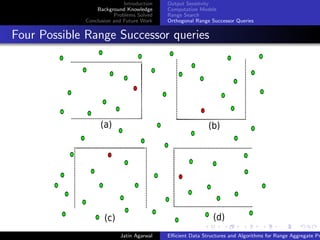
Problem Statements
Given a set S of n points in a plane and an orthogonal query Q of
the form [a, b] × [c, d] where [a, b] is a range on the x-axis and
[c, d] is a range on the y-axis, report the skyline points in S ∩ Q.
Problem 1: Report the skyline inside S ∩ Q. Here
Q = [a, +∞] × [c, +∞].
Problem 2: Count the number of points on the skyline of S ∩ Q.
Here Q = [a, +∞] × [c, +∞].
Problem 3: Report the skyline inside S ∩ Q. Here
Q = [a, +∞] × [c, d].
Problem 4: Count the number of points on the skyline of S ∩ Q.
Here Q = [a, +∞] × [c, d].
Jatin Agarwal Efficient Data Structures and Algorithms for Range Aggregate Pr](https://image.slidesharecdn.com/defence-160706143708/85/MS-Thesis-34-320.jpg)




![Introduction
Background Knowledge
Problems Solved
Conclusion and Future Work
Planar Range Maxima
Planar Range Convex Hull and Related problems
2-sided query
Given any query Q = [a, +∞] × [c, +∞].
query q=(a,c)
Figure: 2-sided query to unbounded on top and right
Jatin Agarwal Efficient Data Structures and Algorithms for Range Aggregate Pr](https://image.slidesharecdn.com/defence-160706143708/85/MS-Thesis-39-320.jpg)




![Introduction
Background Knowledge
Problems Solved
Conclusion and Future Work
Planar Range Maxima
Planar Range Convex Hull and Related problems
2-sided Range counting
count = index[pt] − index[pb] + 1 takes constant O(1) time.
(a,c)
pt
pb
Figure: 2-sided Range Counting
Query Time complexity:O(log n)
Jatin Agarwal Efficient Data Structures and Algorithms for Range Aggregate Pr](https://image.slidesharecdn.com/defence-160706143708/85/MS-Thesis-44-320.jpg)
![Introduction
Background Knowledge
Problems Solved
Conclusion and Future Work
Planar Range Maxima
Planar Range Convex Hull and Related problems
Our results on 2-sided queries
Theorem
Given a set S of n points in R2, we can pre-process S into a data
structure of size O(n) in time O(n log n) such that, given an
2-sided query Q = [a, ∞] × [c, ∞], we can report/count the
maximal points of S ∩ Q in time O(log n + k)/O(log n), where k
is the number of points reported.
Jatin Agarwal Efficient Data Structures and Algorithms for Range Aggregate Pr](https://image.slidesharecdn.com/defence-160706143708/85/MS-Thesis-45-320.jpg)


![Introduction
Background Knowledge
Problems Solved
Conclusion and Future Work
Planar Range Maxima
Planar Range Convex Hull and Related problems
3-sided Reporting query
Report the skyline inside S ∩ Q. Here Q = [a, +∞] × [c, d].
Infy
InfyInfy
(a,d)
(a,c)
Figure: 3-sided query to find maxima
Jatin Agarwal Efficient Data Structures and Algorithms for Range Aggregate Pr](https://image.slidesharecdn.com/defence-160706143708/85/MS-Thesis-48-320.jpg)






![Introduction
Background Knowledge
Problems Solved
Conclusion and Future Work
Planar Range Maxima
Planar Range Convex Hull and Related problems
3-sided Range counting
count =
count[pt] − count[pb] + 1
takes constant O(1) time.
In this example count is
3 = 4 − 1 + 1.
Time complexity:O(log n)
Infy
InfyInfy
1
2
1
2
3
4
5
6
3
4
5
3
4
5
4
56
12
3
pt
pb
(a,d)
(a,c)
Figure: 3-sided Range Counting
Jatin Agarwal Efficient Data Structures and Algorithms for Range Aggregate Pr](https://image.slidesharecdn.com/defence-160706143708/85/MS-Thesis-55-320.jpg)
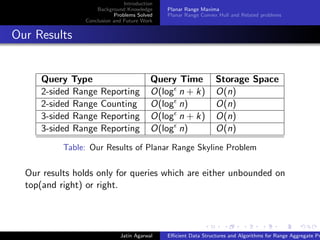
![Introduction
Background Knowledge
Problems Solved
Conclusion and Future Work
Planar Range Maxima
Planar Range Convex Hull and Related problems
Conjecture
Conjecture
Given a set S of n points in R2, it may be possible to pre-process
S into a data structure of size O(n log n) in time O(n log n) such
that, given an 4-sided orthogonal query Q = [a, b] × [c, d], we can
report and count the number of maximal points of S ∩ Q in time
O(log n + k) and O(log n + k) respectively.
Jatin Agarwal Efficient Data Structures and Algorithms for Range Aggregate Pr](https://image.slidesharecdn.com/defence-160706143708/85/MS-Thesis-57-320.jpg)



![Introduction
Background Knowledge
Problems Solved
Conclusion and Future Work
Planar Range Maxima
Planar Range Convex Hull and Related problems
Problem Statements
We are given a set P of n points in R2 and a query
q = [xlt, xrt] × [yb, yt]. We wish to pre-process P into a data
structure such that given an orthogonal query region q, we can
efficiently
Problem 1: Report the points on convex hull of P ∩ q.
Problem 2: Count the number of points on the convex hull of
P ∩ q.
Problem 3: Find the area of the convex hull of P ∩ q.
Problem 4: Find the perimeter of the convex hull of P ∩ q.
Jatin Agarwal Efficient Data Structures and Algorithms for Range Aggregate Pr](https://image.slidesharecdn.com/defence-160706143708/85/MS-Thesis-61-320.jpg)











![Introduction
Background Knowledge
Problems Solved
Conclusion and Future Work
Planar Range Maxima
Planar Range Convex Hull and Related problems
Counting points on a Convex hull
Each candidate convex hull
contribute some part from
array A.
Difference of indices at this
boundaries gives us the
count.
For example
index[p8] − index[p9] + 1 as
shown in figure.
Therefore computing count
for candidate convex hull
takes O(1) time.
p1
p2
p3
p4
p6
p5
p7
p10
p8
p9
p11
p4 p2 p1 p5 p9 p11 p8
A
Jatin Agarwal Efficient Data Structures and Algorithms for Range Aggregate Pr](https://image.slidesharecdn.com/defence-160706143708/85/MS-Thesis-73-320.jpg)
![Introduction
Background Knowledge
Problems Solved
Conclusion and Future Work
Planar Range Maxima
Planar Range Convex Hull and Related problems
Perimeter of the convex hull
We store commutative sum
of perimeter in Array P.
Each candidate convex hull
contribute some perimeter
to total perimeter A.
Difference of indices at this
boundaries gives us the
perimeteri .
P[p8] − P[p9] + 1 gives
perimeter as shown in figure.
Therefore computing
perimeteri for candidate
convex hull takes O(1) time.
p1
p2
p3
p4
p6
p5
p7
p10
p8
p9
p11
p4 p2 p1 p5 p9 p11 p8
A
p42 p41 p43 p46 p411 p48 p44P
Jatin Agarwal Efficient Data Structures and Algorithms for Range Aggregate Pr](https://image.slidesharecdn.com/defence-160706143708/85/MS-Thesis-74-320.jpg)







