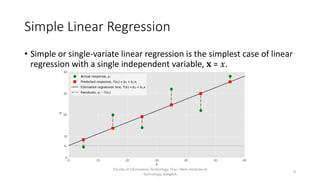
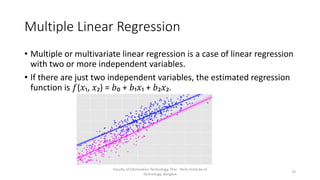
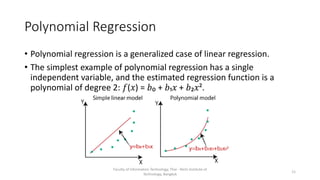
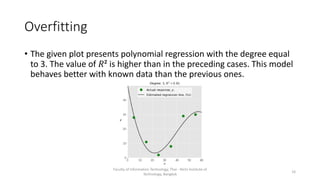
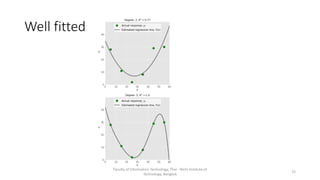
This document discusses different types of linear regression models including simple, multiple, and polynomial linear regression. It provides code examples for implementing linear regression using scikit-learn and statsmodels. Key steps covered include importing packages, providing data, creating and fitting regression models, obtaining results like coefficients and metrics, making predictions on new data, and visualizing models. Types of linear regression covered are simple linear regression with one variable, multiple linear regression with two or more variables, and polynomial regression with higher degree polynomials.

1. Programming for Data
Analysis
Week 9
Dr. Ferdin Joe John Joseph
Faculty of Information Technology
Thai – Nichi Institute of Technology, Bangkok

2. Today’s lesson
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
2
• Linear Regression

3. Prerequisite
• Pandas
• Numpy
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
3

4. New Library needed
• Scikit Learn
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
4

5. Regression
• Regression analysis is one of the most important fields in statistics
and machine learning.
• There are many regression methods available.
• Linear regression is one of them.
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
5

6. Linear Regression
• Linear regression is probably one of the most important and widely
used regression techniques.
• It’s among the simplest regression methods.
• One of its main advantages is the ease of interpreting results.
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
6

7. Types of Linear Regression
• Simple Linear Regression
• Multiple Linear Regression
• Polynomial Regression
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
7

8. Simple Linear Regression
• Simple or single-variate linear regression is the simplest case of linear
regression with a single independent variable, 𝐱 = 𝑥.
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
8

9. Simple Linear Regression
• It starts with a given set of input-output (𝑥-𝑦) pairs (green circles).
• These pairs are your observations.
• For example, the leftmost observation (green circle) has the input 𝑥 =
5 and the actual output (response) 𝑦 = 5.
• The next one has 𝑥 = 15 and 𝑦 = 20, and so on.
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
9

10. Multiple Linear Regression
• Multiple or multivariate linear regression is a case of linear regression
with two or more independent variables.
• If there are just two independent variables, the estimated regression
function is 𝑓(𝑥₁, 𝑥₂) = 𝑏₀ + 𝑏₁𝑥₁ + 𝑏₂𝑥₂.
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
10

11. Polynomial Regression
• Polynomial regression is a generalized case of linear regression.
• The simplest example of polynomial regression has a single
independent variable, and the estimated regression function is a
polynomial of degree 2: 𝑓(𝑥) = 𝑏₀ + 𝑏₁𝑥 + 𝑏₂𝑥².
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
11

12. Underfitting and Overfitting
• Underfitting occurs when a model can’t accurately capture the
dependencies among data, usually as a consequence of its own
simplicity.
• Overfitting happens when a model learns both dependencies among
data and random fluctuations.
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
12

13. Underfitting
• The given plot shows a linear regression line that has a low 𝑅². It
might also be important that a straight line can’t take into account the
fact that the actual response increases as 𝑥 moves away from 25
towards zero. This is likely an example of underfitting.
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
13

14. Overfitting
• The given plot presents polynomial regression with the degree equal
to 3. The value of 𝑅² is higher than in the preceding cases. This model
behaves better with known data than the previous ones.
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
14

15. Well fitted
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
15

16. Linear Relationship
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
16
Positive Linear Relationship Negative Linear Relationship

17. Simple Linear Regression With scikit-learn
There are five basic steps when you’re implementing linear regression:
• Import the packages and classes you need.
• Provide data to work with and eventually do appropriate transformations.
• Create a regression model and fit it with existing data.
• Check the results of model fitting to know whether the model is
satisfactory.
• Apply the model for predictions.
• Visualize
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
17

18. Import the packages and classes you need
• The first step is to import the package numpy and the class
LinearRegression from sklearn.linear_model:
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
18

19. Provide data
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
19

20. Create a model and fit it
model = LinearRegression()
model = LinearRegression().fit(x, y)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
20

21. Get results
• r_sq = model.score(x, y)
• print('coefficient of determination:', r_sq)
• print('intercept:', model.intercept_)
• print('slope:', model.coef_)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
21

22. Predict Response
• y_pred = model.predict(x)
• print('predicted response:', y_pred, sep='n’)
• y_pred = model.intercept_ + model.coef_ * x
• print('predicted response:', y_pred, sep='n')
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
22

23. Predict Response
• x_new = np.arange(5).reshape((-1, 1))
• print(x_new)
• y_new = model.predict(x_new)
• print(y_new)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
23

24. Display in a plot
import matplotlib.pyplot as plt
plt.plot(x, y, label = "actual")
plt.plot(x_new, y_new, label = "Predicted")
plt.legend()
plt.show()
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
24

25. Multiple Linear Regression
• Import packages, classes and data
• Create Model and fit it
• Get results
• Predict Response
• Visualize
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
25

26. Get Data
x = [[0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60, 35]]
y = [4, 5, 20, 14, 32, 22, 38, 43]
x, y = np.array(x), np.array(y)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
26

27. Create Model and fit
model = LinearRegression().fit(x, y)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
27

28. Get Results
r_sq = model.score(x, y)
print('coefficient of determination:', r_sq)
print('intercept:', model.intercept_)
print('slope:', model.coef_)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
28

29. Predict Response
y_pred = model.predict(x)
print('predicted response:', y_pred, sep='n’)
y_pred = model.intercept_ + np.sum(model.coef_ * x, axis=1)
print('predicted response:', y_pred, sep='n’)
y_pred=model.predict(x)
y_pred=model.intercept_+np.sum(model.coef_*x,axis=1)
x_new = [[0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60,
35]]
y_new = model.predict(x_new)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
29

30. Polynomial Regression
• Import packages and classes
• Provide Data
• Create a model and fit it
• Get results
• Predict Response
• Visualize
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
30

31. Import packages and classes
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
31

32. Provide Data
x = np.array([5, 15, 25, 35, 45, 55]).reshape((-1, 1))
y = np.array([15, 11, 2, 8, 25, 32])
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
32

33. Transform input data
transformer = PolynomialFeatures(degree=2, include_bias=False)
transformer.fit(x)
x_ = transformer.transform(x)
x_ = PolynomialFeatures(degree=2, include_bias=False).fit_transform(x)
print(x_)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
33

34. Create a model and fit it
model = LinearRegression().fit(x_, y)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
34

35. Get Results
# Step 4: Get results
r_sq = model.score(x_, y)
intercept, coefficients = model.intercept_, model.coef_
# Step 5: Predict
y_pred = model.predict(x_)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
35

36. Advanced Linear Regression using stats
models
• Import Packages
• Provide Data and Transform inputs
• Create Model and fit it
• Get Results
• Predict Response
• Visualize
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
36

37. Import packages
import statsmodels.api as sm
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
37

38. Provide data and transform inputs
x = [[0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60, 35]]
y = [4, 5, 20, 14, 32, 22, 38, 43]
x, y = np.array(x), np.array(y)
x = sm.add_constant(x)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
38

39. Create Model and fit it
model = sm.OLS(y, x)
results = model.fit()
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
39

40. Get Results
print(results.summary())
print('coefficient of determination:', results.rsquared)
print('adjusted coefficient of determination:', results.rsquared_adj)
print('regression coefficients:', results.params)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
40

41. Predict Response
print('predicted response:', results.fittedvalues, sep='n')
print('predicted response:', results.predict(x), sep='n’)
x_new = sm.add_constant(np.arange(10).reshape((-1, 2)))
print(x_new)
y_new = results.predict(x_new)
print(y_new)
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
41

42. DSA 207 – Linear Regression
• Linear Regression
Faculty of Information Technology, Thai - Nichi Institute of
Technology, Bangkok
42