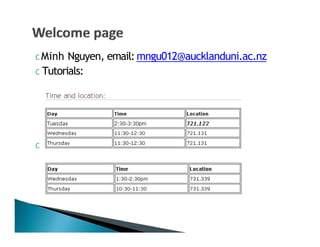
This document discusses floating point numbers and how they are represented in computers using binary rather than decimal. It notes that floating point numbers are approximations and certain calculations may result in numbers like 0.999999999 instead of the expected 1. This is due to the limitations of binary representation. It then explains how floating point numbers use a significand and exponent to represent a wide range of values with limited precision. Finally, it provides some examples of converting between decimal and IEEE 754 single-precision floating point format.

1. Data representation‐ floatingpoints

2. C Minh Nguyen, email: mngu012@aucklanduni.ac.nz
C Tutorials:
C Office hours:

3. C Floating numbers are not accurate represented incomputer
C For example, if one multiplies :
C One might perhaps expect to get a result of exactly 1, which
is the correct answer when applying an exact rational
number or algebraic model. In practice, however, the
result on a digital computer or calculator may prove to be
something such as 0.9999999999999999 (as one might
find when doing the calculation on paper) or,in certain
cases, perhaps 0.99999999923475.
C The latter result seems to indicate a bug, but it is actually
an unavoidable consequence of the use of a binary
floating‐point approximation. Decimal floating‐point,
computer algebra systems, and certain bignum systems
would give either the answer of 1 or
0.9999999999999999...

4. C Fixed‐pointnumbers:
◦ A number of bits sufficient for the precision and range
required must be chosen to store the fractional and integer
parts of a number. For example, using a 32‐bit format, 16 bits
might be used for the integer and 16 for the fraction.

5. C However, using this form of encoding means thatsome
numbers cannot be represented in binary. For
example, for the fraction 1/5 (in decimal, this is 0.2),
the closest one can getis:
C Demonsstration

7. C In the decimal system, we are familiar with floating‐point
numbers of theform:
◦ 1.1030402 × 105 = 1.1030402 × 100000 = 110304.02
C or,more compactly:
◦ 1.1030402E5
C which means "1.103402 times 1 followed by 5 zeroes". We
have a certain numeric value (1.1030402) known as a
"significand", multiplied by a power of 10 (E5, meaning 105
or 100,000), known as an "exponent". If we have a negative
exponent, that means the number is multiplied by a 1 that
many places to the right of the decimal point. For example:
◦ 2.3434E‐6 = 2.3434 × 10‐6 = 2.3434 × 0.000001 = 0.0000023434

8. C Demonstrationmovie:
C http://www.cs.auckland.ac.nz/compsci210s1c/lectures/angela/float.htm
C The advantage of this scheme is that by using the exponent we
can get a much wider range of numbers, even if the number of
" "
" "
digits in the significand,or the numeric precision ,is much
smaller than the range. Similar binary floating‐point formatscan
be defined for computers. There are a number of such schemes,
the most popular has been defined by IEEE (Institute of
Electrical & ElectronicEngineers).
C A 32‐bit float value is sometimes called a "real32" or a "single",
meaning single‐precision floating‐point value .
C A 64‐bit float is sometimes called a "real64" or a "double",
meaning "double‐precision floating‐pointvalue".

9. C Exercise1:ConvertC2200000from IEEE754Floating Point
(Single Precision) todecimal
C Exercise2:Convert2.25from Decimal to IEEE754Floating
Point (SinglePrecision)
C Exercise3:ConvertC210000016from IEEE754Floating
Point (Single Precision) todecimal
C Exercise4:Convert2.25from Decimal to IEEE754Floating
Point (SinglePrecision)