The document provides links to video lectures on multiplication techniques involving bases of 10, 20, and 50. It also includes videos on multiplying multi-digit numbers. There are also sections on division, approximation, ratio comparison, squaring numbers using different bases, cubing numbers, and some miscellaneous math problems. The document serves as a reference for learning different multiplication, division, and number operations through online video tutorials.

2. MULTIPLICATION – VIDEO LECTURES
These videos will guide you to quicker multiplication. Anything which is quick saves
your time during problem solving in competitive exams.
Multiplication techniques involving base 10, 20 and 50
1. http://www.youtube.com/watch?v=Rgw9Ik5ZGaY
2. http://www.youtube.com/watch?v=SV1dC1KAl_U
3. http://www.youtube.com/watch?v=E2Az_6gH74w
Multiplication of a three digit number and a two digit number
• http://www.youtube.com/embed?listType=user_uploads&list=tecmath
Multiply two 4-digit number (You can use the same concept to multiply two 2-
digit numbers or two 3-digit numbers and so on)
• https://www.youtube.com/watch?v=7X85-tylGTQ
P.S : goo.gl/arGhzt @ PrepVelvet

3. DIVISON
There are three golden rules of approximation:
• Range of approximation should be 2% with respect to the actual result.
• Approximation should be done only if the options are at a considerable gap,
say 5% atleast.
• One of the key things to be kept in mind while doing approximation is the
direction of the approximation i.e., one should know if the actual result will be
more or less than the approximated result.
We should know that in any division, if the numerator and the denominator are
both either increased or decreased by the same percentage, then the result will
be exactly the same. While it is practically not possible to find such situations
always, we will use this to know the direction while doing approximation for the
above calculation:

4. APPROXIMATION 1
Eliminate the unit digit of both the numerator and the denominator
Now, the objective is to break the numerator into the parts of the denominator.
354 = 209(50% of 418) + 145
145 = 105(25% of 418 approx.) + 40
40 = 10% of 418
Hence, net value = 85% = 0.85
Is this value more or less than the actual value?
Let us compare it with the actual result = 0.8483, which is a slightly less than the
approximated result of ours.

5. APPROXIMATION 2
Eliminate the unit and tens place digit of both the numerator and the
denominator
35 = 20.5(50% 0f 41) + 14.5
14.5 = 12(30% of 40 approx.) +2.5 = 30% of 41 + 6% of 41(approx.)
[Since 0.41 = 1% of 41]
Hence, net value = 86% = 0.86. This is slightly more than the actual value.

6. RATIO COMPARISON
Cross Multiplication
• Cross multiplying the numerator of the 1st fraction with the denominator of
the 2nd fraction and denominator of the 1st fraction with the numerator of the
2nd fraction,
• Since, 198 is greater than 195; so the 1st fraction (11/15) is greater than the
2nd fraction (13/18).

7. RATIO COMPARISON
Decimal Comparision

8. RATIO COMPARISON
Percentage Comparison
• In the 1st case, percentage change in numerator (100%↑) = percentage change in
denominator (100%↑), So ratios are equal.
• In the 2nd case, percentage change in the numerator (200%↑) > percentage
change in the denominator(100%↑). So the 2nd ratio is greater than the 1st ratio.
• In the 3rd case, percentage change in the numerator (200%↑) < percentage
change in the denominator (300%↑). So the 1st ratio is greater than the 2nd ratio.

9. SQUARE OF NUMBERS

10. SQUARE – BASE 10
Square of 9.
1. 9 is 1 less than 10, decrease it still further to 8. This is the left side of our
answer. •
2. On the right hand side put the square of the deficiency that is 12.
3. Hence, the answer is 81. •
Similarly, 82 = 64, 72 = 49. •
For numbers above 10, instead of looking at the deficit we look at the
surplus.
For example,
112 = (11 + 1). 10 + 12 = 121
142 = (14 + 4). 10 + 42 = 18 . 10 + 16 = 196
and so on.

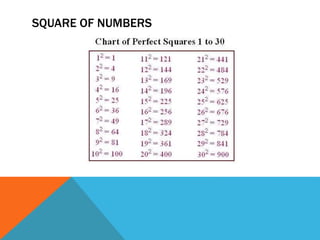
11. SQUARE- BASE 50N
Square of 64
1. Number is close to 50. Assume 50 as the base.
2. 64² = (50+14)² = 50² + 2*50*14 + 14² = 2500 + 1400 + 196
3. This may be written as :
64² = [(100’s in (base)]² + Surplus|Surplus²
= 25 + 14|196 = (39+1)|96 = 4096
Similarly
• (68)2 = 25 + 18 | 324 = 46 | 24 = 4624
• (76)2 = 25 + 26 | 676 = 57 | 76 = 5776
• (42)2 = 25 − 8 | 64 = 17 | 24 = 1724

12. SQUARE- BASE 50N
Square of 113
1. Number is close to 100. So we take 100 as the base.
2. 113² = (100 + 13)² = 100² + 2*100*13 + 13²
3. This may be written as : { note n = 2 }
113² = [100’s in (Base)]2 + 2 × Surplus | Surplus2
= 100 + 26|169
= 12769
• Had this been 162, we would have multiplied 3 in surplus before adding it into
[100’s in (Base)]2 because assumed base here is 150.
• (162)2 = [100’s in (Base)]2 + 3 × Surplus | Surplus2
• = 225 + 3 × 12 | 122 = 262 | 44

13. SQUARE OF NUMBERS – 10ª METHOD
This method is applied when the number is close to 10n.
With base as 10n, find the surplus or deficit (×) Again answer can be arrived at in two
parts (B + 2x) |x2
The right-hand part will consist of n digits. Add leading zeros or carry forward the extra
to satisfy this condition.
1082 = (100 + 2 × 8) | 82 = 116 | 64 = 11664
932 = (100 – 2 × 7) | (−7)2 = 86 | 49 ⇒ 8649
10062 = (1000 + 2 × 6) | 62 = 10|12 | 036 = 1012036
The right-hand part will consist of 2 digits. Add leading zeros or carry forward the extra
to satisfy this condition.
632 = (25 + 13) | 132 = 38 | 169 = 3969
382 = (25 – 12) + (−12)2 = 13 | 144 = 1444

14. SQUARING @ PREPVELVET
http://goo.gl/W5HbNY

15. CUBING
We can find the cube of any number close to a power of 10 say 10n with base = 10n by
finding the surplus or the deficit (x). The answer will be obtained in three parts.
B + 3x | 3 . x2 | x3
The left two parts will have n digits.
1043
Base B = 100 and surplus = x = 4
(100 + 3 × 4)|3 × 42|43 = 112|48|64 = 1124864
1093
Base B = 100 and x = 9
(100 + 3 × 9)|3 × 92 |93 = 127|243|729 = 1295029
983
Base B = 100 and x = −2
(100 − 3 × 2) | 3 × (−2)2 | (−2)3 = 94 | 12 | −8 = 94 | 11 | 100 – 8 = 941192

16. SQUARE AND CUBE ROOT
Watch this video to grasp the concept
goo.gl/5yRBDM
Alternate link :
https://www.youtube.com/watch?v=f61A_iQtVv0

17. MISC
N1 -> Numerator 1
N2 -> Numerator 2
D1 -> Denominator 1
D2 -> Denominator 2
1. 6x+13x = 12x+ 7x => x= 0 {No need to argue over this :P }
2. (x+7)(x+10) = (x+14)(x+5) = > x = 0 {Why ? Coz 7*10=14*5}
3. Same numerator
1/(2x-1) + 1/(3x-2) = 0 = > 2x-1+3x-2 = 0 => 5x -3 = 0 => x=5/3
4. (2x+9)/(2x+7) = (2x+7)/(2x+9) => 4x+16 =0 => x= -4

18. MISC
D1+D2 = D3+D4 = 2x -16 => x=8
X-3+x-9 = 2(x-12) => (x-6) = 0 => x=6
Observe: N1 + D1 = N2 + D2 = 2x + 8.
Therefore, x = −4.