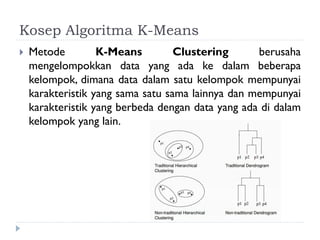
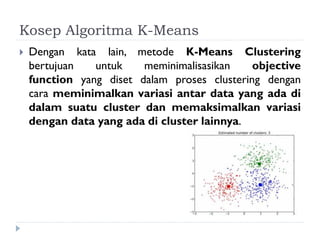
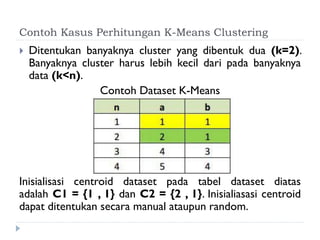
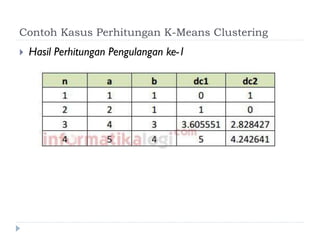
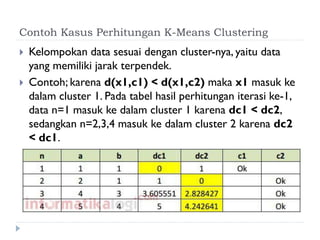
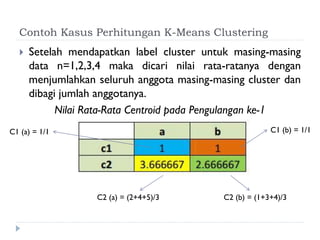
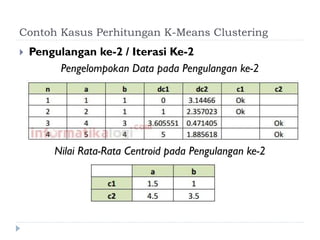
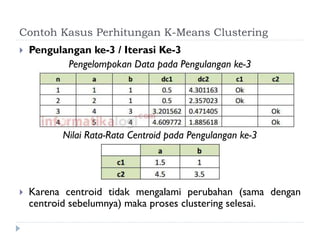
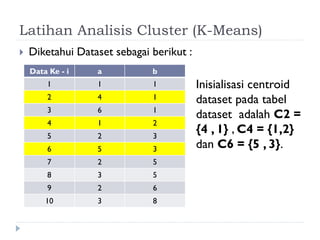
Dokumen ini membahas tentang algoritma k-means yang digunakan untuk analisis cluster dalam data mining. Algoritma ini dapat mengelompokkan data berdasarkan atribut tertentu ke dalam sejumlah cluster dengan meminimalisasi variasi intra-cluster dan memaksimalkan variasi inter-cluster. K-means adalah metode unsupervised yang memerlukan inisialisasi centroid dan memiliki sensitivitas terhadap pembangkitan centroid awal.

1. Algoritma K-Means : Analisis Cluster
pada Data Mining
Dedi Darwis, M.Kom.

2. Kosep Algoritma K-Means
 Clustering adalah pengelompokan sejumlah obyek yang
besar berdasarkan ciri atau atribut tertentu ke dalam
sejumlah kelompok atau cluster.
 Algoritma K-Mean merupakan algoritma yang relatif
sederhana untuk mengklasifikasikan atau
mengelompokkan sejumlah besar obyek dengan atribut
tertentu ke dalam kelompok-kelompok sebanyak K.
 K-Mean salah satu metode data clustering non hirarki
yang berusaha mempartisi data yang ado ke dalam
bentuk satu atau lebih cluster atau kelompok.

3. Kosep Algoritma K-Means
 Terdapat dua jenis data clustering yang sering
dipergunakan dalam proses pengelompokan data yaitu
Hierarchical dan Non-Hierarchical, dan K-Means
merupakan salah satu metode data clustering non-
hierarchical atau Partitional Clustering.

4. Kosep Algoritma K-Means
 Metode K-Means Clustering berusaha
mengelompokkan data yang ada ke dalam beberapa
kelompok, dimana data dalam satu kelompok mempunyai
karakteristik yang sama satu sama lainnya dan mempunyai
karakteristik yang berbeda dengan data yang ada di dalam
kelompok yang lain.

5. Kosep Algoritma K-Means
 Dengan kata lain, metode K-Means Clustering
bertujuan untuk meminimalisasikan objective
function yang diset dalam proses clustering dengan
cara meminimalkan variasi antar data yang ada di
dalam suatu cluster dan memaksimalkan variasi
dengan data yang ada di cluster lainnya.

6. Kosep Algoritma K-Means
 K-Means merupakan metode data clustering yang
digolongkan sebagai metode pengklasifikasian
yang bersifat unsupervised (tanpa arahan).
 Pengkategorian metode-metode pengklasifikasian data
antara supervised dan unsupervised classification
didasarkan pada adanya dataset yang data itemnya sudah
sejak awal mempunyai label kelas atau tidak.
 Untuk data yang sudah mempunyai label kelas, metode
pengklasifikasian yang digunakan merupakan
metode supervised classification dan untuk data yang
belum mempunyai label kelas, metode pengklasifikasian
yang digunakan adalah metode unsupervised
classification.

7. Cara Kerja Algoritma K-Means
1. Tentukan jumlah cluster
2. Alokasikan data ke dalam cluster secara random
3. Hitung centroid/rata-rata dari data yang ada di masing-
masing cluster
4. Alokasikan masing-masing data ke centroid/rata-rata
terdekat
5. Kembali ke Step 3, apabila masih ada data yang
berpindah cluster atau apabila perubahan nilai centroid,
ada yang di atas nilai threshold yang ditentukan atau
apabila perubahan nilai pada objective function yang
digunakan di atas nilai threshold yang ditentukan

8. Karakteristik K-Means
 K-Means sangat cepat dalam proses clustering
 K-Means sangat sensitif pada pembangkitan centroid awal
secara random
 Memungkinkan suatu cluster tidak mempunyai anggota
 Hasil clustering dengan K-Means bersifat tidak unik (selalu
berubah-ubah) – terkadang baik, terkadang jelek
 K-means sangat sulit untuk mencapai global optimum

9. Karakteristik K-Means
 Memperhatikan input dalam algoritma K-Means, dapat
dikatakan bahwa algoritma ini hanya mengolah data kuantitatif
atau numerik.
 Sebuah basis data tidak mungkin hanya berisi satu macam tipe
data saja, akan tetapi beragam tipe.
Sebuah basis data dapat berisi data-
data dengan tipe sebagai berikut: binary, nominal, ordinal,
interval dan ratio.
 Berbagai macam atribut dalam basis data yang berbeda tipe
disebut sebagai data multivariate.
Tipe data seperti nominal dan ordinal harus diolah terlebih
dahulu menjadi data numerik (bisa dilakukan dengan cara
diskritisasi), sehingga dapat diberlakukan algoritma K-
Means dalam pembentukan clusternya.

10. Contoh Kasus Perhitungan K-Means Clustering
 Ditentukan banyaknya cluster yang dibentuk dua (k=2).
Banyaknya cluster harus lebih kecil dari pada banyaknya
data (k<n).
Contoh Dataset K-Means
Inisialisasi centroid dataset pada tabel dataset diatas
adalah C1 = {1 , 1} dan C2 = {2 , 1}. Inisialiasasi centroid
dapat ditentukan secara manual ataupun random.

11. Contoh Kasus Perhitungan K-Means Clustering
 Untuk pengulangan berikutnya (pengulangan ke-1 sampai
selesai), centroid baru dihitung dengan menghitung nilai
rata-rata data pada setiap cluster.
 Jika centroid baru berbeda dengan centroid sebelumnya,
maka proses dilanjutkan ke langkah berikutnya. Namun
jika centroid yang baru dihitung sama dengan centroid
sebelumnya, maka proses clustering selesai.

12. Contoh Kasus Perhitungan K-Means Clustering
 Rumus yang digunakan untuk menghitung distance space
atau jarak data dengan centroid menggunakan Euclidiean
Distance.
Persamaan Euclidean Distance :

13. Contoh Kasus Perhitungan K-Means Clustering
 Pengulangan ke-1 / Iterasi ke-1
 Jarak data dengan Centroid C1 adalah:

14. Contoh Kasus Perhitungan K-Means Clustering
 Jarak data dengan Centroid C2 adalah:
 Untuk seterusnya, hitung jarak pada setiap baris data

15. Contoh Kasus Perhitungan K-Means Clustering
 Hasil Perhitungan Pengulangan ke-1

16. Contoh Kasus Perhitungan K-Means Clustering
 Kelompokan data sesuai dengan cluster-nya, yaitu data
yang memiliki jarak terpendek.
 Contoh; karena d(x1,c1) < d(x1,c2) maka x1 masuk ke
dalam cluster 1. Pada tabel hasil perhitungan iterasi ke-1,
data n=1 masuk ke dalam cluster 1 karena dc1 < dc2,
sedangkan n=2,3,4 masuk ke dalam cluster 2 karena dc2
< dc1.

17. Contoh Kasus Perhitungan K-Means Clustering
 Setelah mendapatkan label cluster untuk masing-masing
data n=1,2,3,4 maka dicari nilai rata-ratanya dengan
menjumlahkan seluruh anggota masing-masing cluster dan
dibagi jumlah anggotanya.
Nilai Rata-Rata Centroid pada Pengulangan ke-1
C2 (a) = (2+4+5)/3 C2 (b) = (1+3+4)/3
C1 (a) = 1/1 C1 (b) = 1/1

18. Contoh Kasus Perhitungan K-Means Clustering
 Pengulangan ke-2 / Iterasi Ke-2
Pengelompokan Data pada Pengulangan ke-2
Nilai Rata-Rata Centroid pada Pengulangan ke-2

19. Contoh Kasus Perhitungan K-Means Clustering
 Pengulangan ke-3 / Iterasi Ke-3
Pengelompokan Data pada Pengulangan ke-3
Nilai Rata-Rata Centroid pada Pengulangan ke-3
 Karena centroid tidak mengalami perubahan (sama dengan
centroid sebelumnya) maka proses clustering selesai.

20. Latihan Analisis Cluster (K-Means)
 Diketahui Dataset sebagai berikut :
Data Ke - i a b
1 1 1
2 4 1
3 6 1
4 1 2
5 2 3
6 5 3
7 2 5
8 3 5
9 2 6
10 3 8
Inisialisasi centroid
dataset pada tabel
dataset adalah C2 =
{4 , 1} , C4 = {1,2}
dan C6 = {5 , 3}.