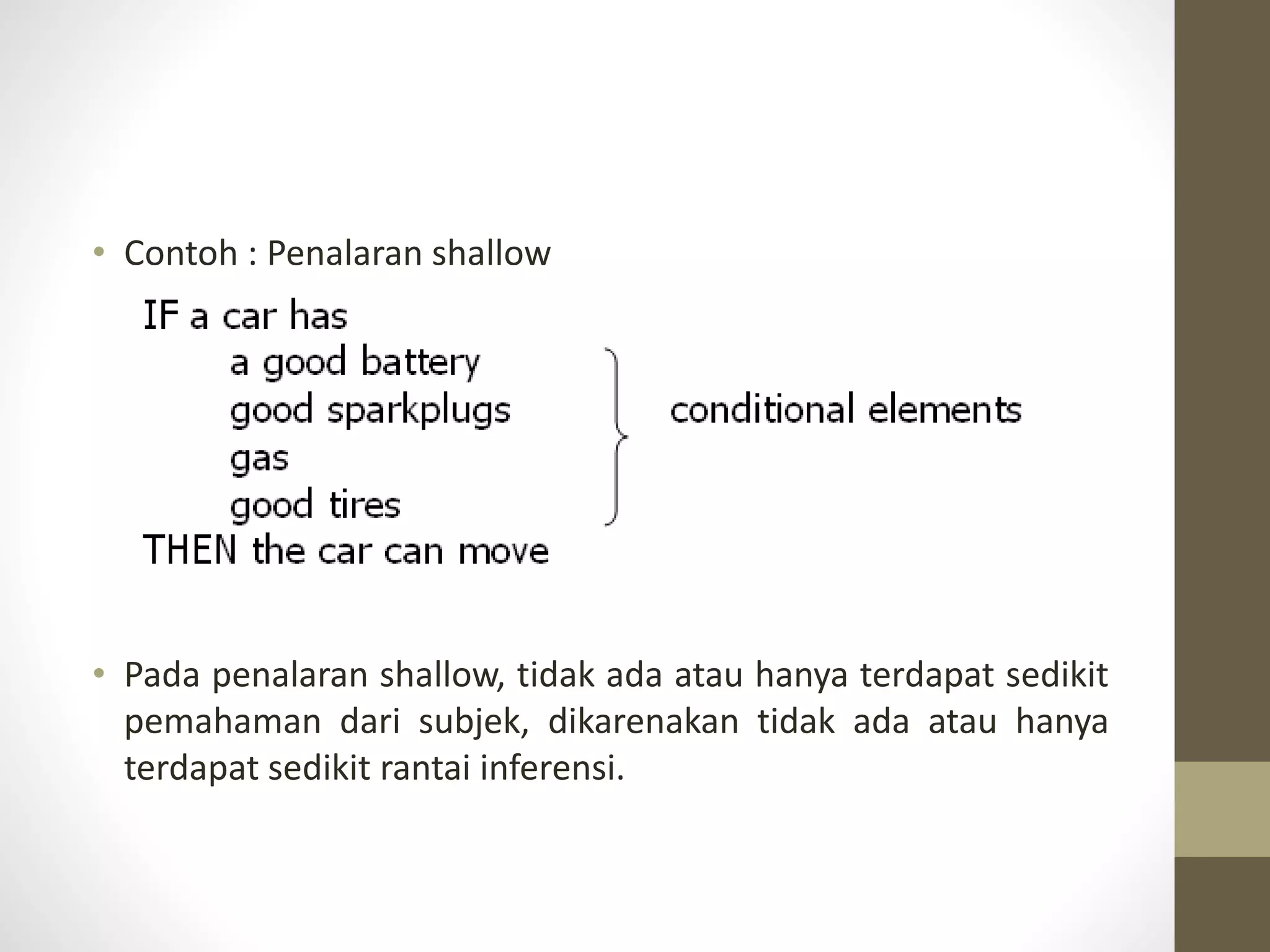
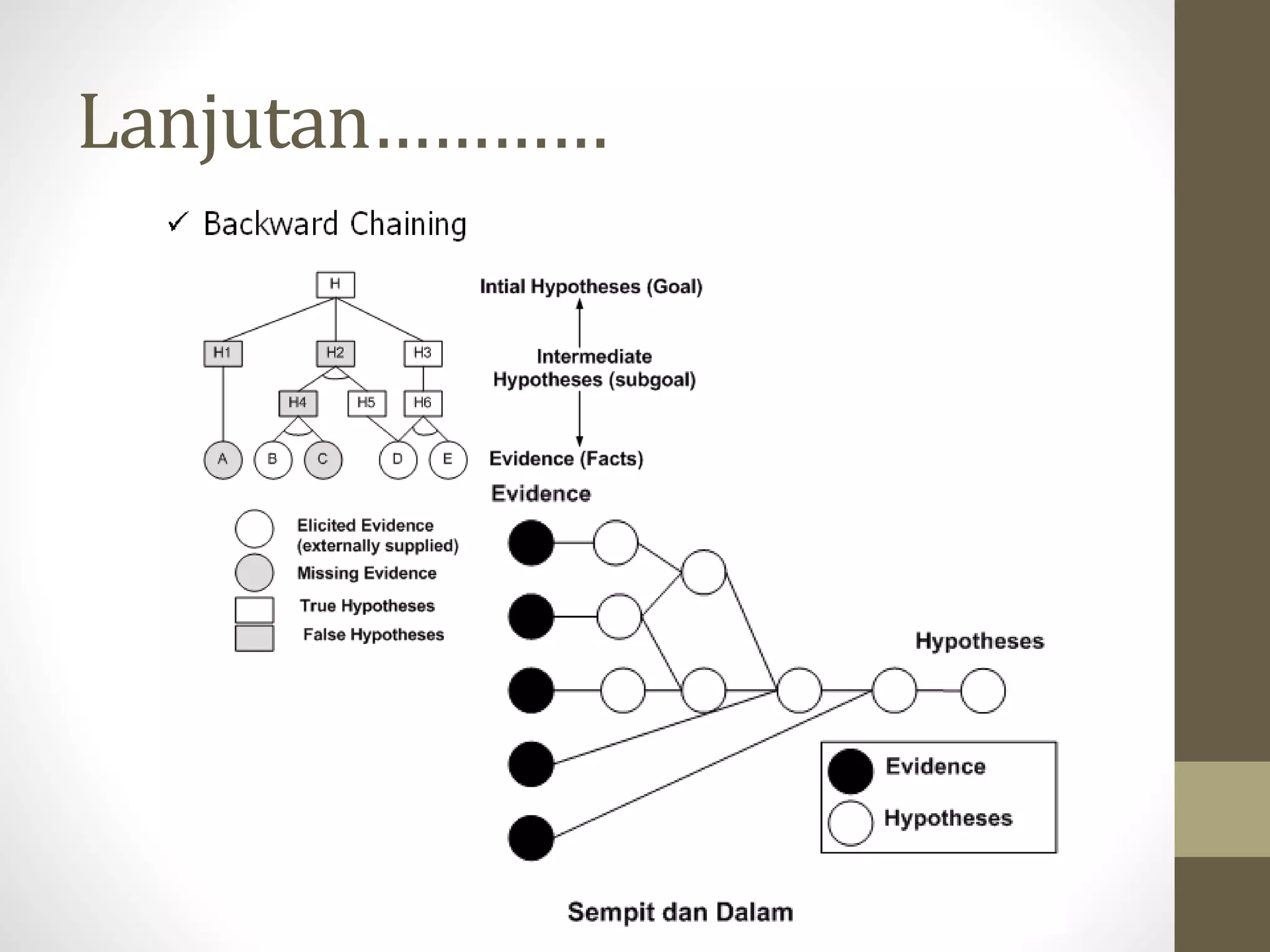
Dokumen ini menjelaskan berbagai metode inferensi dalam graf, pohon, dan lattice, serta menerangkan konsep logika deduktif, silogisme, dan aturan inferensi. Berbagai jenis inferensi, seperti modus ponens dan modus tollens, serta kritik terhadap logika proposisi dan penggunaan logika predikat juga dibahas. Selain itu, dokumen ini mencakup penalaran causal, rantai inferensi seperti forward dan backward chaining, serta konsep meta-knowledge dalam sistem pakar.