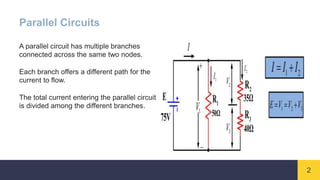
The current division rule is used to determine the current flowing through different branches of a parallel circuit. It states that the total current entering a parallel circuit will divide among the branches based on each branch's resistance. The current through each branch can be calculated using the current division rule formula, which relates the branch currents to the total current and the resistances of each branch. The current division rule is useful for circuit analysis and design, though it assumes resistances are purely resistive without stray capacitance or inductance effects.

1. Current Division Rule
SlideMake.com

2. 1
Introduction
The current division rule is a principle used
in electrical circuit analysis.
It helps determine the current flowing
through different branches of a parallel
circuit.
It is based on the concept that the total
current entering a junction is equal to the
sum of the currents leaving the junction.

3. 2
Parallel Circuits
A parallel circuit has multiple branches
connected across the same two nodes.
Each branch offers a different path for the
current to flow.
The total current entering the parallel circuit
is divided among the different branches.

4. 3
Current Division Rule Formula
The current division rule is mathematically
represented as follows:
- I1 = (I
R2) / (R1 + R2)
- I2 = (I
R1) / (R1 + R2)
- I1 and I2 represent the currents flowing
through R1 and R2 respectively.
- I is the total current entering the parallel
circuit.
- R1 and R2 are the resistances of the
respective branches.

5. 4
Applying the Current Division Rule
To apply the current division rule, first
identify the resistances of the parallel
branches.
Determine the total current entering the
parallel circuit.
Substitute the values into the current
division rule formula.

6. 5
Example Problem
Consider a parallel circuit with two
resistors: R1 = 10 ohms and R2 = 20
ohms.
The total current entering the parallel circuit
is 2 Amperes.
Using the current division rule formula, we
can find the currents flowing through each
branch.

7. 6
Applying the Formula
Substituting the given values into the
current division rule formula:
- I1 = (2
20) / (10 + 20) = 0.8 Amperes
- I2 = (2
10) / (10 + 20) = 1.2 Amperes

8. 7
Results
The current through R1 is 0.8 Amperes.
The current through R2 is 1.2 Amperes.
The sum of the currents through both
branches equals the total current entering
the parallel circuit.

9. 8
Practical Applications
The current division rule is often used in
electronic circuit design.
It helps analyze and optimize the current
distribution in parallel circuits.
It is particularly useful in designing circuits
with multiple components that require
different current levels.

10. 9
Limitations
The current division rule assumes that the
resistances in the parallel branches are
purely resistive.
It does not consider the effects of stray
capacitance or inductance.
It is most accurate when the resistances
are significantly larger than the reactances.

11. 10
Conclusion
The current division rule is a valuable tool
for analyzing parallel circuits.
It allows us to determine the currents
flowing through different branches.
By understanding and applying this rule,
engineers and designers can optimize
circuit performance.