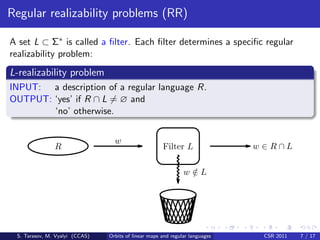
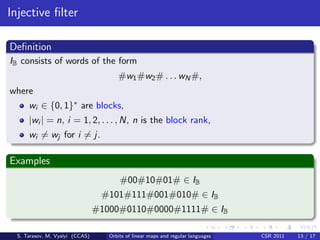
This document discusses the relationships between orbits of linear maps and regular languages. It shows that the chamber hitting problem (CHP) and permutation filter realizability problem are Turing equivalent. It also shows that the injective filter and surjective filter realizability problems are decidable by reducing them to problems about orbits. However, the regular realizability problem for the track product of the periodic and permutation filters is undecidable, as it can reduce the undecidable zero in the upper right corner problem.

1. Orbits of Linear Maps and Regular Languages
S. Tarasov, M. Vyalyi
Dorodnitsyn Computing Center of RAS
CSR 2011
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 1 / 17

2. Contents
1 Orbits of linear maps
2 Regular realizability (RR)
3 Examples of relation between RR and linear algebra
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 2 / 17

3. Chamber hitting problem
Definition
An orbit OrbΦ x is {Φk x : k ∈ Z+ }, where Φ : Qd → Qd is a linear map
and x ∈ Qd .
Definition
A chamber HS = {x ∈ Qd : sign(hi (x)) = si for 1 i m}, where hi are
affine functions and s ∈ {±1, 0}m is a sign pattern.
Chamber hitting problem (CHP)
INPUT: Φ, x0 , h1 , . . . , hm , s.
OUTPUT: ‘yes’ if OrbΦ x0 ∩ Hs = ∅ and
‘no’ otherwise.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 3 / 17

4. Chamber hitting problem
Definition
An orbit OrbΦ x is {Φk x : k ∈ Z+ }, where Φ : Qd → Qd is a linear map
and x ∈ Qd .
Definition
A chamber HS = {x ∈ Qd : sign(hi (x)) = si for 1 i m}, where hi are
affine functions and s ∈ {±1, 0}m is a sign pattern.
Chamber hitting problem (CHP)
INPUT: Φ, x0 , h1 , . . . , hm , s.
OUTPUT: ‘yes’ if OrbΦ x0 ∩ Hs = ∅ and
‘no’ otherwise.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 3 / 17

5. Chamber hitting problem
Definition
An orbit OrbΦ x is {Φk x : k ∈ Z+ }, where Φ : Qd → Qd is a linear map
and x ∈ Qd .
Definition
A chamber HS = {x ∈ Qd : sign(hi (x)) = si for 1 i m}, where hi are
affine functions and s ∈ {±1, 0}m is a sign pattern.
Chamber hitting problem (CHP)
INPUT: Φ, x0 , h1 , . . . , hm , s.
OUTPUT: ‘yes’ if OrbΦ x0 ∩ Hs = ∅ and
‘no’ otherwise.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 3 / 17

6. Special cases: the orbit problem
Orbit problem
INPUT: Φ, x, y .
OUTPUT: ‘yes’ if y ∈ OrbΦ x and
‘no’ otherwise.
In this case the chamber is {y }.
Theorem (Kannan, Lipton, 1986)
There exists a polynomial time algorithm for the orbit problem.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 4 / 17

7. Special cases: the orbit problem
Orbit problem
INPUT: Φ, x, y .
OUTPUT: ‘yes’ if y ∈ OrbΦ x and
‘no’ otherwise.
In this case the chamber is {y }.
Theorem (Kannan, Lipton, 1986)
There exists a polynomial time algorithm for the orbit problem.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 4 / 17

8. Problems reducible to CHP
Skolem problem
INPUT: a1 , . . . , ad ; b1 , . . . , bd .
xn — a linear recurrent sequence
d
xn = ai xn−i , (n > d), xn = bn (1 n d)
i=1
OUTPUT: ‘yes’ if xn = 0 for some n and
‘no’ otherwise.
Positivity problem
INPUT: a1 , . . . , ad ; b1 , . . . , bd ; xn is LRS.
OUTPUT: ‘yes’ if xn > 0 for all n and
‘no’ otherwise.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 5 / 17

9. Problems reducible to CHP
Skolem problem
INPUT: a1 , . . . , ad ; b1 , . . . , bd .
xn — a linear recurrent sequence
d
xn = ai xn−i , (n > d), xn = bn (1 n d)
i=1
OUTPUT: ‘yes’ if xn = 0 for some n and
‘no’ otherwise.
Positivity problem
INPUT: a1 , . . . , ad ; b1 , . . . , bd ; xn is LRS.
OUTPUT: ‘yes’ if xn > 0 for all n and
‘no’ otherwise.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 5 / 17

10. State of the art
Open questions
Is CHP decidable? Is Skolem problem decidable? Is positivity problem
decidable?
Known decidability results for small d
d =2 d =3 d =4 d =5
Skolem folklore Vereshchagin, 1985 Halava et al.,
2005
Pos. pr. Halava et al., Laohakosol,
2006 Tangsupphathawat,
2009
CHP Sechin, 2011
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 6 / 17

11. Regular realizability problems (RR)
A set L ⊂ Σ∗ is called a filter. Each filter determines a specific regular
realizability problem:
L-realizability problem
INPUT: a description of a regular language R.
OUTPUT: ‘yes’ if R ∩ L = ∅ and
‘no’ otherwise.
w
R Filter L w ∈R∩L
w∈L
/
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 7 / 17

12. Permutation filter
Definition
PB ⊂ {#, 0, 1}∗ consists of permutation words, i.e., words of the form
#w1 #w2 # . . . wN #,
where
wi ∈ {0, 1}∗ are blocks,
|wi | = n, i = 1, 2, . . . , N (n is the block rank),
N = 2n , n 1,
each binary word of length n is a block.
Examples
#00#11#10#01# ∈ PB
#10#11#00#01# ∈ PB
#10#01#00#11# ∈ PB
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 8 / 17

13. Orbits vs Regular realizability
Theorem (Tarasov, Vyalyi, 2010)
CHP and PB -realizability problem are Turing equivalent.
From PB -realizability to CHP
Reduction starts from a Q-linear extension of the transition monoid.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 9 / 17

14. Orbits vs Regular realizability
Theorem (Tarasov, Vyalyi, 2010)
CHP and PB -realizability problem are Turing equivalent.
From PB -realizability to CHP
Reduction starts from a Q-linear extension of the transition monoid.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 9 / 17

15. From CHP to PB -realizability
The idea is to represent an arithmetic computation in a ‘natural’ form.
The main construction
R1 , R2 — regular languages.
How to check that there exists an integer n such that
Card({w : |w | = n ∧ w ∈ R1 }) = Card({w : |w | = n ∧ w ∈ R2 })?
(♣)
Regular expression
E = #((R1 ∩ R2 )#)∗ ((R1 R2 )#(R2 R1 )#)∗ ((R1 ∩ R2 )#)∗
(♣) is equivalent to E ∩ PB = ∅.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 10 / 17

16. From CHP to PB -realizability
The idea is to represent an arithmetic computation in a ‘natural’ form.
The main construction
R1 , R2 — regular languages.
How to check that there exists an integer n such that
Card({w : |w | = n ∧ w ∈ R1 }) = Card({w : |w | = n ∧ w ∈ R2 })?
(♣)
Regular expression
E = #((R1 ∩ R2 )#)∗ ((R1 R2 )#(R2 R1 )#)∗ ((R1 ∩ R2 )#)∗
(♣) is equivalent to E ∩ PB = ∅.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 10 / 17

17. From CHP to PB -realizability
The idea is to represent an arithmetic computation in a ‘natural’ form.
The main construction
R1 , R2 — regular languages.
How to check that there exists an integer n such that
Card({w : |w | = n ∧ w ∈ R1 }) = Card({w : |w | = n ∧ w ∈ R2 })?
(♣)
Regular expression
E = #((R1 ∩ R2 )#)∗ ((R1 R2 )#(R2 R1 )#)∗ ((R1 ∩ R2 )#)∗
(♣) is equivalent to E ∩ PB = ∅.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 10 / 17

18. From CHP to PB -realizability
The idea is to represent an arithmetic computation in a ‘natural’ form.
The main construction
R1 , R2 — regular languages.
How to check that there exists an integer n such that
Card({w : |w | = n ∧ w ∈ R1 }) = Card({w : |w | = n ∧ w ∈ R2 })?
(♣)
Regular expression
E = #((R1 ∩ R2 )#)∗ ((R1 R2 )#(R2 R1 )#)∗ ((R1 ∩ R2 )#)∗
(♣) is equivalent to E ∩ PB = ∅.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 10 / 17

19. More examples of relation between RR and linear algebra
undecidable track product of the periodic and permutation filter
unknown permutation filter
decidable surjective filter injective filter
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 11 / 17

20. Surjective filter
Definition
SB consists of words of the form
#w1 #w2 # . . . wN #,
where
wi ∈ {0, 1}∗ are blocks,
|wi | = n, i = 1, 2, . . . , N, n is the block rank,
each binary word of length n is a block.
Examples
#00#00#11#10#01# ∈ SB
#10#11#10#00#01# ∈ SB
#10#01#00#01#11# ∈ SB
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 12 / 17

21. Injective filter
Definition
IB consists of words of the form
#w1 #w2 # . . . wN #,
where
wi ∈ {0, 1}∗ are blocks,
|wi | = n, i = 1, 2, . . . , N, n is the block rank,
wi = wj for i = j.
Examples
#00#10#01# ∈ IB
#101#111#001#010# ∈ IB
#1000#0110#0000#1111# ∈ IB
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 13 / 17

22. Decidability results
Theorem
IB -realizability problem is decidable.
SB -realizability problem is decidable.
Proofs are based on converting IB -realizability problem (resp.,
SB -realizability problem) to a problem about orbits.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 14 / 17

23. Decidability results
Theorem
IB -realizability problem is decidable.
SB -realizability problem is decidable.
Proofs are based on converting IB -realizability problem (resp.,
SB -realizability problem) to a problem about orbits.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 14 / 17

24. An undecidable problem
Zero in the Upper Right Corner Problem (ZURC)
INPUT: A1 , . . . , AN are D × D integer matrices.
OUTPUT: ‘yes’ if there exists a sequence j1 , . . . , j such that
(Aj1 Aj2 . . . Aj )1D = 0 and
‘no’ otherwise.
Theorem (Bell, Potapov, 2006)
The ZURC problem is undecidable for N = 2 and D = 18.
The ZURC problem is reduced to the regular realizability problem for the
track product of periodic and permutation filters.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 15 / 17

25. An undecidable problem
Zero in the Upper Right Corner Problem (ZURC)
INPUT: A1 , . . . , AN are D × D integer matrices.
OUTPUT: ‘yes’ if there exists a sequence j1 , . . . , j such that
(Aj1 Aj2 . . . Aj )1D = 0 and
‘no’ otherwise.
Theorem (Bell, Potapov, 2006)
The ZURC problem is undecidable for N = 2 and D = 18.
The ZURC problem is reduced to the regular realizability problem for the
track product of periodic and permutation filters.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 15 / 17

26. An undecidable problem
Zero in the Upper Right Corner Problem (ZURC)
INPUT: A1 , . . . , AN are D × D integer matrices.
OUTPUT: ‘yes’ if there exists a sequence j1 , . . . , j such that
(Aj1 Aj2 . . . Aj )1D = 0 and
‘no’ otherwise.
Theorem (Bell, Potapov, 2006)
The ZURC problem is undecidable for N = 2 and D = 18.
The ZURC problem is reduced to the regular realizability problem for the
track product of periodic and permutation filters.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 15 / 17

27. Track product
For languages L1 ⊂ ({#} ∪ Σ1 )∗ , L2 ⊂ ({#} ∪ Σ2 )∗ the track product
L1 L2 ⊂ ({#} ∪ Σ1 × Σ2 )∗ .
Projections
a1 a2 a3
... # # ...
b 1 b2 b3
π1 π2
. . . # a1 a2 a3 # . . . . . . # b 1 b 2 b3 # . . .
Definition of L1 L2
L1 L2 = {w ∈ ({#} ∪ Σ1 × Σ2 )∗ | π1 w ∈ L1 ; π2 w ∈ L2 }
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 16 / 17

28. Track product
For languages L1 ⊂ ({#} ∪ Σ1 )∗ , L2 ⊂ ({#} ∪ Σ2 )∗ the track product
L1 L2 ⊂ ({#} ∪ Σ1 × Σ2 )∗ .
Projections
a1 a2 a3
... # # ...
b 1 b2 b3
π1 π2
. . . # a1 a2 a3 # . . . . . . # b 1 b 2 b3 # . . .
Definition of L1 L2
L1 L2 = {w ∈ ({#} ∪ Σ1 × Σ2 )∗ | π1 w ∈ L1 ; π2 w ∈ L2 }
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 16 / 17

29. Track product of periodic and permutation filters
Definitions
Periodic filter PerΣ ⊂ ({#} ∪ Σ)∗ consists of words of the form
#w #w # . . . w #,
where w ∈ {0, 1}∗ .
Definition of the permutation filter PΣ over the alphabet {#} ∪ Σ is
similar to the binary case.
Theorem
ZURC ≤m (PerΣ1 PΣ2 )-regular realizability for |Σ1 | = 2, |Σ2 | = 648.
Informally, the periodic part is to represent a sequence of matrices and the
permutation part is to encode the condition that the URC entry is 0.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 17 / 17

30. Track product of periodic and permutation filters
Definitions
Periodic filter PerΣ ⊂ ({#} ∪ Σ)∗ consists of words of the form
#w #w # . . . w #,
where w ∈ {0, 1}∗ .
Definition of the permutation filter PΣ over the alphabet {#} ∪ Σ is
similar to the binary case.
Theorem
ZURC ≤m (PerΣ1 PΣ2 )-regular realizability for |Σ1 | = 2, |Σ2 | = 648.
Informally, the periodic part is to represent a sequence of matrices and the
permutation part is to encode the condition that the URC entry is 0.
S. Tarasov, M. Vyalyi (CCAS) Orbits of linear maps and regular languages CSR 2011 17 / 17