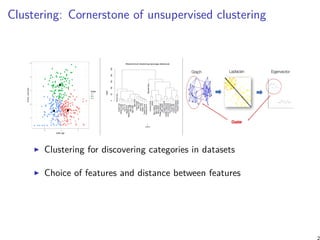
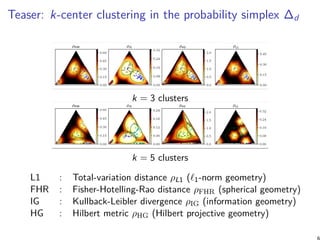
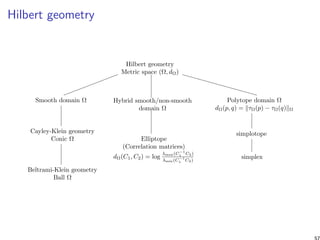
- The document discusses different geometric approaches for clustering multinomial distributions, including total variation distance, Fisher-Rao distance, Kullback-Leibler divergence, and Hilbert cross-ratio metric. - It benchmarks k-means clustering using these four geometries on the probability simplex, finding that Hilbert geometry clustering yields good performance with theoretical guarantees. 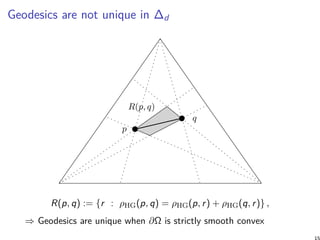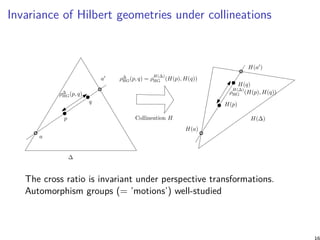- The Hilbert cross-ratio metric defines a non-Riemannian Hilbert geometry on the simplex with polytopal balls, and satisfies information monotonicity properties desirable for clustering distributions.

1. Clustering in Hilbert geometry for machine
learning
Frank Nielsen1 Ke Sun2
1Sony Computer Science Laboratories Inc, Japan
2CSIRO, Australia
December 2018
@FrnkNlsn
https://arxiv.org/abs/1704.00454
1

2. Clustering: Cornerstone of unsupervised clustering
Clustering for discovering categories in datasets
Choice of features and distance between features
2

3. Motivations
Which geometry and distance are appropriate for a space of
probability distributions? for a space of correlation matrices?
Information geometry [5] focuses on the differential-geometric
structures associated to spaces of parametric distributions...
Benchmark different geometric space modelings
3

4. The probability simplex space
Many tasks in text mining, machine learning, computer vision
deal with multinomial distributions (or mixtures thereof),
living on the probability simplex
Which distance and underlying geometry should we
consider for handling the space of multinomials?
(L1): Total-variation distance and ℓ1-norm geometry
(FRH): Fisher-Rao distance and spherical Riemannian
geometry
(IG): Kullback-Leibler/f -divergences and information geometry
(HG): Hilbert cross-ratio metric and Hilbert projective
geometry
Benchmark experimentally these different geometries by
considering k-means/k-center clusterings of multinomials
4

5. The space of multinomial distributions
Probability simplex (standard simplex):
∆d := {p = (λ0
p, . . . , λd
p ) : pi > 0,
∑d
i=0 λi
p = 1}.
Multinomial distribution
X = (X0, . . . , Xd ) ∼ Mult(p = (λ0
p, . . . , λd
p ), m) with
probability mass function:
Pr(X0 = m0, . . . , Xd = md ) =
m!
∏d
i=0 mi !
d∏
i=0
(
λi
p
)mi
,
d∑
i=0
mi = m
Binomial (d = 1), Bernoulli (d = 1, m = 1),
multinoulli/categorical/discrete (m = 1 and d > 1)
. . . . . .
. . . . . .
. . . . . . . . . . . .
sampling
inference
k
i=1 wiMult(pi)
Categorical data
set of normalized histograms point set in the probability simplex
p1
p2
p3
H1
H2
H3
5

6. Teaser: k-center clustering in the probability simplex ∆d
k = 3 clusters
k = 5 clusters
L1 : Total-variation distance ρL1 (ℓ1-norm geometry)
FHR : Fisher-Hotelling-Rao distance ρFHR (spherical geometry)
IG : Kullback-Leibler divergence ρIG (information geometry)
HG : Hilbert metric ρHG (Hilbert projective geometry)
6

7. Review of four types of
geometry for the
probability simplex ∆d
7

8. Total variation distance and ℓ1-norm geometry
L1 metric distance ρL1:
ρL1(p, q) =
d∑
i=0
|λi
p − λi
q|
Total variation is ρTV(p, q) = 1
2∥λp − λq∥1 ≤ 1
Satisfies the information monotonicity by coarse-graining the
histogram bins
(TV is a f -divergence for generator f (u) = 1
2|u − 1|):
0 ≤ ρL1(p′
, q′
) ≤ ρL1(p, q),
for p′ = Ap and q′ = Aq for a positive d′ × d
column-stochastic matrix A, with d′ < d
ℓ1-norm-induced distance:
ρL1(p, q) = ∥λp − λq∥1
8

9. The shape of ℓ1-balls in ∆d
For trinomials in ∆2 (with λ2 = 1 − (λ0 + λ1)), the ρL1
distance is given by:
ρL1(p, q) = |λ0
p − λ0
q| + |λ1
p − λ1
q| + |λ0
q − λ0
p + λ1
q − λ1
p|.
ℓ1-distance is polytopal: cross-polytope
Z = conv(±ei : i ∈ [d]) also called co-cube (orthoplex)
Shape of ℓ1-balls:
BallL1 (p, r) = (λp ⊕ rZ) ∩ H∆d
In 2D, regular octahedron cut by H∆2 = hexagonal shapes.
9

10. Visualizing the 1D/2D/3D shapes of L1 balls in ∆d
Illustration courtesy of ’Geometry of Quantum States’, [1]
10

11. Fisher-Hotelling-Rao Riemannian geometry (1930)
Fisher metric tensor [gij] (constant positive curvature):
gij(p) =
δij
λi
p
+
1
λ0
p
.
Statistical invariance yields unique Fisher metric [2]
Distance is a geodesic length (Levi-Civita connection ∇LC
with metric-compatible parallel transport)
Rao metric distance between two multinomials on Riemannian
manifold (∆d , g):
ρFHR(p, q) = 2 arccos
( d∑
i=0
√
λi
pλi
q
)
.
Can be embedded in the positive orthant of an Euclidean
d-sphere of Rd+1 by using the square root representation
λ →
√
λ = (
√
λ0, . . . ,
√
λd )
11

12. Kullback-Leibler divergence and information geometry
Kullback-Leibler (KL) divergence ρIG:
ρIG(p, q) =
d∑
i=0
λi
p log
λi
p
λi
q
.
Satisfies the information monotonicity (f -divergence with
f (u) = − log u) when coarse-graining ∆d → ∆d′ (with
d′ < d): 0 ≤ If (p′ : q′) ≤ If (p : q). Fisher-Rao ρFHR does
not satisfy the information monotonicity
Dualistic structure: dually flat manifold (∆d , g, ∇m, ∇e)
(exponential connection ∇e and mixture connection ∇m, with
∇LC = ∇m+∇e
2 ), or expected α-geometry (∆d , g, ∇−α, ∇α)
for α ∈ R. Dual parallel transport that is metric compatible.
∆d is both an exponential family and a mixture family (= a
dually flat space)
12

13. Hilbert cross ratio metric & geometry
Log cross ratio distance:
(metric satisfying the triangle inequality)
ρHG(M, M′
) =
{
log |A′M||AM′|
|A′M′||AM| , M ̸= M′,
0 M = M′.
Euclidean line segments are geodesics (but not unique,
Busemann’s G-space)
Hilbert Geometry (HG) holds for any open convex compact
subset domain (e.g., ∆d , elliptope of correlation matrices)
13

14. Euclidean shape of balls in Hilbert projective geometry
Hilbert balls in ∆d : hexagons shapes (2D) [10], rhombic
dodecahedra (3D), polytopes [4] with d(d + 1) facets in
dimension d.
1.5
3.0
4.5
6.0
Not Riemannian/differential-geometric geometry because
infinitesimally small balls have not ellipsoidal shapes. (Tissot
indicatrix in Riemannian geometry)
A video explaining the shapes of Hilbert balls:
https://www.youtube.com/watch?v=XE5x5rAK8Hk&t=1s
14

15. Geodesics are not unique in ∆d
p
q
R(p, q)
R(p, q) := {r : ρHG(p, q) = ρHG(p, r) + ρHG(q, r)} ,
⇒ Geodesics are unique when ∂Ω is strictly smooth convex
15

16. Invariance of Hilbert geometries under collineations
∆
H(∆)p
q H(p)
H(q)
ρ∆
HG(p, q) ρ
H(∆)
HG (H(p), H(q))
a
a
H(a)
H(a )
Collineation H
ρ∆
HG(p, q) = ρ
H(∆)
HG (H(p), H(q))
The cross ratio is invariant under perspective transformations.
Automorphism groups (= ’motions’) well-studied
16

17. Hilbert geometry generalizes Cayley-Klein hyperbolic
geometry
Defined for a quadric domain
(curved elliptical/hyperbolic Mahalanobis distances [6])
Video: https://www.youtube.com/watch?v=YHJLq3-RL58
17

18. Computing Hilbert metric distance in general
M (t0 ≤ 0) and M′ (t1 ≥ 1): intersection points of the line
(1 − t)p + tq with ∂∆d .
Expression using t0 and t1:
ρHG(p, q) = log
(1 − t0)t1
(−t0)(t1 − 1)
= log
(
1 −
1
t0
)
−log
(
1 −
1
t1
)
.
18

19. Relationship with Birkhoff projective geometry
Instead of considering the (d − 1)-dimensional simplex ∆d ,
consider the the pointed cone Rd
+,∗.
Birkhoff projective metric on positive histograms:
ρBG(˜p, ˜q) := log maxi,j∈[d]
˜pi ˜qj
˜pj ˜qi
is scale-invariant ρBG(α˜p, β˜q) = ρBG(˜p, ˜q), for any α, β > 0.
O
˜p
˜q
p
q
e1 = (1, 0)
e2 = (0, 1)
∆1
R2
+,∗
ρHG(p, q)
ρBG(˜p, ˜q)
19

20. Hilbert simplex distance satisfies the information
monotonicity
Birhkoff proved (1957) :
ρBG(M˜p, M˜q) ≤ κ(M) × ρBG(˜p, ˜q)
where κ(M) is the contraction ratio of the binning scheme.
κ(M) :=
√
a(M) − 1
√
a(M) + 1
< 1, a(M) := maxi,j,k,l
Mi,kMj,l
Mj,kMi,l
< ∞.
A first example of non-separable distance that preserves
information monotonicity!
20

21. Shape of Hilbert balls in an open simplex
A ball in the Hilbert simplex geometry has a Euclidean
polytope shape with d(d + 1) facets [4]
In 2D, Hilbert balls have 2(2 + 1) = 6 hexagonal shapes
varying with center locations. In 3D, the shape of balls are
rhombic-dodecahedron
When the domain is not simplicial, Hilbert balls can have
varying complexities [10]
No metric tensor in Hilbert geometry because infinitesimally
the ball shapes are polytopes and not ellipsoids.
Hilbert geometry can be studied via Finsler geometry
21

22. Isometry of Hilbert simplex geometry with a normed vector
space (∆d
, ρHG) ∼= (V d
, ∥ · ∥NH)
V d = {v ∈ Rd+1 :
∑
i vi = 0} ⊂ Rd+1
Map p = (λ0, . . . , λd ) ∈ ∆d to v(x) = (v0, . . . , vd ) ∈ V d :
vi
=
1
d + 1

d log λi
−
∑
j̸=i
log λj

 = log λi
−
1
d + 1
∑
j
log λj
.
λi
=
exp(vi )
∑
j exp(vj)
.
Norm ∥ · ∥NH in V d defined by the shape of its unit ball
BV = {v ∈ V d : |vi − vj| ≤ 1, ∀i ̸= j}.
Polytopal norm-induced distance:
ρV (v, v′
) = ∥v − v′
∥NH = inf
{
τ : v′
∈ τ(BV ⊕ {v})
}
,
Norm does not satisfy parallelogram law (no inner product)
22

23. Visualizing the isometry: (∆d
, ρHG) ∼= (V d
, ∥ · ∥NH)
23

24. Some distance profiles in ∆d
Reference point (3/7,3/7,1/7)
24

25. Some distance profiles in ∆d
Reference point (5/7,1/7,1/7)
25

26. Comparisons of four main distances for 1D case
Rao distance (=circle arc length, Riemanian geometry):
ρFHR(p, q) = 2 arccos
(
√
λpλq +
√
(1 − λp)(1 − λq)
)
.
KL divergence (dually flat ±1-geometry):
ρIG(p, q) = λp log
λp
λq
+ (1 − λp) log
1 − λp
1 − λq
.
L1 distance (norm geometry):
ρIG(p, q) = |λp − λq|
Hilbert distance (metric geometry):
ρHG(p, q) = log
λp
1 − λp
− log
λq
1 − λq
.
26

27. Benchmarking these
geometries with
center-based clustering
27

28. k-means++ clustering (seeding initialization)
For an arbitrary distance D, define the k-means objective
function (NP-hard to minimize):
ED(Λ, C) =
1
n
n∑
i=1
minj∈{1,...,k}D(pi : cj)
k-means++: Pick uniformly at random at first seed c1, and
then iteratively choose the (k − 1) remaining seeds according
to the following probability distribution:
Pr(cj = pi ) =
D(pi , {c1, . . . , cj−1})
∑n
i=1 D(pi , {c1, . . . , cj−1})
(2 ≤ j ≤ k).
A randomized seeding initialization of k-means, can be further
locally optimized using Lloyd’s batch iterative updates, or
Hartigan’s single-point swap heuristic [9], etc.
28

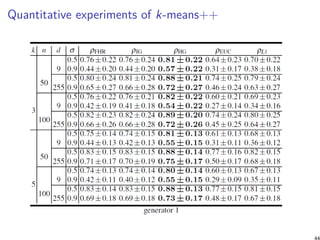
29. Performance analysis of k-means++ [8]
Let κ1 and κ2 be two constants such that κ1 defines the
quasi-triangular inequality property:
D(x : z) ≤ κ1 (D(x : y) + D(y : z)) , ∀x, y, z ∈ ∆d
,
and κ2 handles the symmetry inequality:
D(x : y) ≤ κ2D(y : x), ∀x, y ∈ ∆d
.
Theorem
The generalized k-means++ seeding guarantees with high
probability a configuration C of cluster centers such that:
ED(Λ, C) ≤ 2κ2
1(1 + κ2)(2 + log k)E∗
D(Λ, k)
29

30. Performance analysis of k-means++ in a metric space
In any metric space (X, d), the k-means++ wrt the squared
metric distance d2 is 16(2 + log k)-competitive.
Proof: Symmetric distance (κ2 = 1). Quasi-triangular inequality
property:
d(p, q) ≤ d(p, q) + d(q, r),
d2
(p, q) ≤ (d(p, q) + d(q, r))2
,
d2
(p, q) ≤ d2
(p, q) + d2
(q, r) + 2d(p, q)d(q, r).
Let us apply the inequality of arithmetic and geometric means:
√
d2(p, q)d2(q, r) ≤
d2(p, q) + d2(q, r)
2
.
Thus we have
d2
(p, q) ≤ d2
(p, q)+d2
(q, r)+2d(p, q)d(q, r) ≤ 2(d2
(p, q)+d2
(q, r)).
That is, the squared metric distance satisfies the 2-approximate
triangle inequality, and κ1 = 2.
30

31. Performance analysis of k-means++
In any normed space (X, ∥ · ∥), the k-means++ with
D(x, y) = ∥x − y∥2 is 16(2 + log k)-competitive.
In any inner product space (X, ⟨·, ·⟩), the k-means++ with
D(x, y) = ⟨x − y, x − y⟩ is 16(2 + log k)-competitive.
Hilbert simplex geometry is isometric to a normed vector
space [4] (Theorem 3.3):
(∆d
, ρHG) ≃ (V d
, ∥ · ∥NH)
Theorem
k-means++ seeding in a Hilbert simplex geometry in fixed
dimension is 16(2 + log k)-competitive.
31

32. Clustering in ∆2 with k-means++
k = 3 clusters
k = 5 clusters
32

33. k-Center clustering
Cost function for a k-center clustering with centers C (|C| = k) is:
fD(Λ, C) = maxpi ∈Λmincj ∈C D(pi : cj)
For Hilbert simplex clustering, consider the equivalent normed
space:
r∗
HG = minc∈∆d maxi∈{1,...,n}ρHG(pi , c),
r∗
NH = minv∈V d maxi∈{1,...,n}∥vi − v∥NH.
33

34. k-Center clustering: farthest first traversal heuristic
Guaranteed approximation factor of 2 in any metric space [3]
34

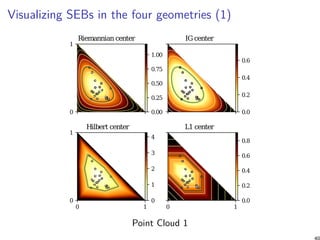
35. Smallest Enclosing Ball (SEB)
Given a finite point set {p1, . . . , pn} ∈ ∆d , the SEB in Hilbert
simplex geometry is centered at
c∗
= arg min
c∈∆d
maxi∈{1,...,n}ρHG(c, xi ),
with radius
r∗
= minc∈∆d maxi∈{1,...,n}ρHG(c, xi ).
Decision problem can be solved by Linear Programming (LP),
and optimization as a LP-type problem [7]
Do not scale well in high dimensions
35

36. Fast approximations for the smallest enclosing ball
Start from an initial point, compute farthest point to current
center, displace center along a geodesic to farthest point, repeat!
36

37. Convergence rate
0 100 200 300
#iterations
0.0
0.2
0.4
0.6
0.8
1.0
Hilbertdistance
d=9; n=10
d=255; n=10
d=9; n=100
d=255; n=100
0 100 200 300
#iterations
0.0
0.2
0.4
0.6
0.8
1.0
relativeHilbertdistance
d=9; n=10
d=255; n=10
d=9; n=100
d=255; n=100
Hilbert distance with the true Hilbert center
Hilbert distance between the current minimax center and the true
center (left) or their Hilbert distance divided by the Hilbert radius
of the dataset (right). The plot is based on 100 random points in
∆9/∆255.
37

38. Examples of smallest enclosing balls in HG and HNG
0
1
Simplex
2 -2
2
-2
After isometry
0
1
2
3
4
0.0
0.8
1.6
2.4
3.2
0
1
Simplex
2 -2
2
-2
After isometry
0
1
2
3
4
0.0
0.8
1.6
2.4
3.2
3 points on the border
38

39. Examples of smallest enclosing balls in HG and HNG
0
1
Simplex
2 -2
2
-2
After isometry
0
1
2
3
4
0.0
0.8
1.6
2.4
3.2
0
1
Simplex
2 -2
2
-2
After isometry
0
1
2
3
4
0.0
0.8
1.6
2.4
3.2
2 points on the border
39

40. Visualizing SEBs in the four geometries (1)
0
1
Riemannian center IG center
0 1
0
1
Hilbert center
0 1
L1 center
0.00
0.25
0.50
0.75
1.00
0.0
0.2
0.4
0.6
0
1
2
3
4
0.0
0.2
0.4
0.6
0.8
Point Cloud 1
40

41. Visualizing smallest enclosing balls (2)
0
1
Riemannian center IG center
0 1
0
1
Hilbert center
0 1
L1 center
0.0
0.3
0.6
0.9
1.2
0.0
0.2
0.4
0.6
0.8
0
1
2
3
4
0.0
0.2
0.4
0.6
0.8
Point Cloud 2
41

42. Visualizing smallest enclosing balls (3)
0
1
Riemannian center IG center
0 1
0
1
Hilbert center
0 1
L1 center
0.0
0.3
0.6
0.9
1.2
0.00
0.25
0.50
0.75
1.00
0
1
2
3
4
0.00
0.25
0.50
0.75
1.00
Point Cloud 3
42

43. Quantitative experiments: Protocol
pick uniformly a random center c = (λ0
c, . . . , λd
c ) ∈ ∆d .
any random sample p = (λ0, . . . , λd ) associated with c is
independently generated by
λi
=
exp(log λi
c + σϵi )
∑d
i=0 exp(log λi
c + σϵi )
,
where σ > 0= noise level parameter, and each ϵi follows
independently a standard Gaussian distribution (generator 1)
or the Student’s t-distribution (5 dof, generator 2).
perform clustering based on the configurations n ∈ {50, 100},
d ∈ {9, 255}, σ ∈ {0.5, 0.9},
ρ ∈ {ρFHR, ρIG, ρHG, ρEUC, ρL1}. The number of clusters k is
set to the ground truth.
repeat the clustering experiment based on 300 different
random datasets. The performance is measured by the
normalized mutual information (NMI, the larger the better). 43

44. Quantitative experiments of k-means++
44

45. Quantitative experiments of k-means++
45

46. k-means++: Positive histograms (non-normalized)
d = 10, N = 50 random samples. σ = noise level.
random sample p multiplied by a random scalar ∼ Γ(10, 0.1).
For each configuration, repeat 300 runs and report the mean and
standard
k σ ρIG+ ρrIG+ ρsIG+ ρBG
3 0.5 0.66 ± 0.21 0.67 ± 0.20 0.66 ± 0.21 0.86 ± 0.18
3 0.9 0.37 ± 0.16 0.38 ± 0.19 0.37 ± 0.19 0.62 ± 0.22
5 0.5 0.68 ± 0.13 0.68 ± 0.12 0.70 ± 0.12 0.85 ± 0.11
5 0.9 0.42 ± 0.10 0.43 ± 0.11 0.44 ± 0.12 0.63 ± 0.13
46

47. Quantitative experiments of k-center
47

48. Quantitative experiments of k-center
48

49. Discussion
Experimentally, we observe that
HG > FHR > IG
HG even better for large amount of noise
Intuitively, HG balls are more compact and better capture the
clustering structure
Not surprisingly, Euclidean geometry gets the poorest score!
49

50. A Hilbert geometry for the
elliptope = space of
correlation matrices
50

51. Elliptope: Space of correlation matrices
Cd
= {Cd×d : C ≻ 0; Cii = 1, ∀i}
C is convex: If C1, C2 ∈ C, then (1 − λ)C1 + λC2 ∈ C for
0 < λ < 1.
51

52. Printed 3D elliptopes
52

53. Distances between correlation matrices
Hilbert distance in the elliptope:
ρHG(C1, C2) = log
∥C1 − C′
2∥∥C′
1 − C2∥
∥C1 − C′
1∥∥C2 − C′
2∥
.
with C′
1 and C′
2 the intersection correlation matrices with the
boundary of the elliptope (no closed form, bisection method in
practice)
Fröbenius distance, L2 norm (Euclidean geometry)
L1 norm
Log-det divergence:
ρLD(C1, C2) = tr(C1C−1
2 ) − log |C1C−1
2 | − d.
53

54. Hilbert/Birkhoff elliptope distance formula
Birkhoff projective metric between covariance matrices:
ρBG(Σ1, Σ2) = log
λmax(Σ−1
1 Σ2)
λmin(Σ−1
1 Σ2)
= ∥ log λ(Σ−1
1 Σ2)∥var
Hilbert metric between correlation matrices:
ρHG(C1, C2) = log
λmax(C−1
1 C2)
λmin(C−1
1 C2)
Invariance properties:
ρHG(C1, C2) = ρHG(C−1
1 , C−1
2 )
ρHG(AC1B, AC2B) = ρHG(C1, C2), ∀A, B ∈ GL(d)
54

55. Experiments: k-means++ on correlation matrices
n = 100 3 × 3 matrices with k = 3 clusters (points in C3, cluster of
almost identical size)
Each cluster is independently generated according to
P ∼ W−1
(I3×3, ν1),
Ci ∼ W−1
(P, ν2),
where W−1(A, ν) = inverse Wishart distribution with scale matrix
A and ν degrees of freedom
Ci is a point in the cluster associated with P.
500 independent runs
ν1 ν2 ρHG ρEUC ρL1 ρLD
4 10 0.62 ± 0.22 0.57±0.21 0.56±0.22 0.58±0.22
4 30 0.85 ± 0.18 0.80±0.20 0.81±0.19 0.82±0.20
4 50 0.89 ± 0.17 0.87±0.17 0.86±0.18 0.88±0.18
5 10 0.50 ± 0.21 0.49±0.21 0.48±0.20 0.47±0.21
5 30 0.77 ± 0.20 0.75±0.21 0.75±0.21 0.75±0.21
5 50 0.84 ± 0.19 0.82±0.19 0.82±0.20 0.84 ± 0.18
55

56. Experiments with Thompson metric on covariance matrices
ρTG(P, Q) := maxi | log λi (P−1
Q)|.
Matrix Pi belongs to a cluster c generated based on
Pi = Qcdiag(Li )Q⊤
c + σAi A⊤
i , where Qc is a random matrix of
orthonormal columns, Li follows a gamma distribution, the entries
of (Ai )d×d follow iid. standard Gaussian distribution, and σ =
noise level parameter.
Li σ ρIG ρrIG ρsIG ρTG
Γ(2, 1) 0.1 0.81 ± 0.09 0.82 ± 0.10 0.81 ± 0.10 0.81 ± 0.09
Γ(2, 1) 0.3 0.51 ± 0.11 0.54 ± 0.11 0.53 ± 0.11 0.52 ± 0.11
Γ(5, 1) 0.1 0.93 ± 0.07 0.93 ± 0.08 0.92 ± 0.08 0.92 ± 0.08
Γ(5, 1) 0.3 0.70 ± 0.10 0.72 ± 0.12 0.71 ± 0.10 0.70 ± 0.11
56

57. Hilbert geometry
Hilbert geometry
Metric space (Ω, dΩ)
Smooth domain Ω
Cayley-Klein geometry
Conic Ω
Beltrami-Klein geometry
Ball Ω
Polytope domain Ω
dΩ(p, q) = τΩ(p) − τΩ(q) Ω
simplex
simplotope
Hybrid smooth/non-smooth
domain Ω
Elliptope
(Correlation matrices)
dΩ(C1, C2) = log
λmax(C−1
1 C2)
λmin(C−1
1 C2)
57

58. Summary and conclusion [11]
Introduced Hilbert/Birkhoff geometry for the probability
simplex (= space of categorical distributions) and the
elliptope (= space of correlation matrices). But also
simplotope (product of simplices), etc.
Hilbert simplex geometry is isometric to a normed vector
space (hilds for any Hilbert polytopal geometry)
Non-separable distance that satisfies the information
monotonicity (contraction ratio of linear operator)
Novel closed form Hilbert/Birkhoff distance formula for the
correlation (metric) and covariance matrices (projective
metric)
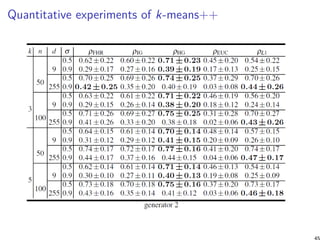
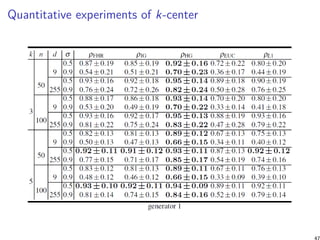
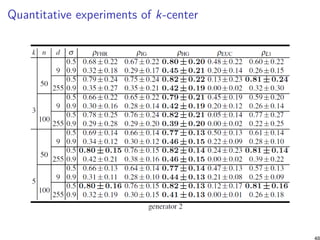
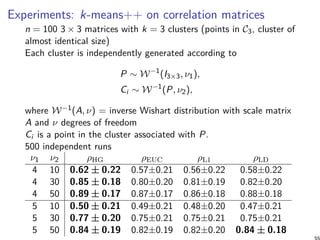
Benchmark experimentally four types of geometry for k-means
and k-center clusterings
Hilbert/Birkhoff geometry experimentally well-suited for
58

59. References I
Ingemar Bengtsson and Karol Życzkowski.
Geometry of quantum states: an introduction to quantum entanglement.
Cambridge university press, 2017.
L. L. Campbell.
An extended čencov characterization of the information metric.
American Mathematical Society, 98(1):135–141, 1986.
Teofilo F Gonzalez.
Clustering to minimize the maximum intercluster distance.
Theoretical Computer Science, 38:293–306, 1985.
Bas Lemmens and Roger Nussbaum.
Birkhoff’s version of Hilbert’s metric and its applications in analysis.
Handbook of Hilbert Geometry, pages 275–303, 2014.
Frank Nielsen.
An elementary introduction to information geometry.
ArXiv e-prints, August 2018.
Frank Nielsen, Boris Muzellec, and Richard Nock.
Classification with mixtures of curved Mahalanobis metrics.
In IEEE International Conference on Image Processing (ICIP), pages 241–245, 2016.
Frank Nielsen and Richard Nock.
On the smallest enclosing information disk.
Information Processing Letters, 105(3):93–97, 2008.
Frank Nielsen and Richard Nock.
Total Jensen divergences: Definition, properties and k-means++ clustering, 2013.
arXiv:1309.7109 [cs.IT].
59

60. References II
Frank Nielsen and Richard Nock.
Further heuristics for k-means: The merge-and-split heuristic and the (k, l)-means.
arXiv preprint arXiv:1406.6314, 2014.
Frank Nielsen and Laëtitia Shao.
On balls in a polygonal Hilbert geometry.
In 33st International Symposium on Computational Geometry (SoCG 2017). Schloss
Dagstuhl–Leibniz-Zentrum fuer Informatik, 2017.
Frank Nielsen and Ke Sun.
Clustering in Hilbert simplex geometry.
CoRR, abs/1704.00454, 2017.
60