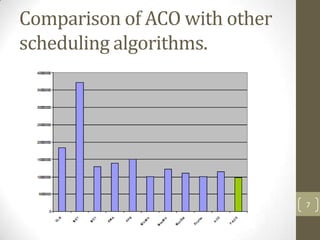
This document discusses using machine learning algorithms for job scheduling in a grid computing environment. It aims to minimize makespan, the total time to complete all tasks, by learning from past scheduling experiences. It proposes using ant colony optimization, where artificial ants probabilistically choose task-machine pairs to incrementally find optimal schedules. The algorithm is compared to other scheduling methods and extended to online scheduling by classifying jobs with attributes to appropriate machines. A feasibility study demonstrates classification and scheduling of test jobs using machine learning tools.

1. Job Scheduling in Grid Environment using
machine learning Algorithms
GUIDE: T R SWAPNA
JAYAKRISHNAN B
CB.EN.P2CSE12007
1

2. Motivation
• The resource scheduling in grid is a NP complete problem
• The choice of the best pairs of jobs and resources cannot be
determined accurately.
• Only way it can do this is by past experience.
• This gives high scope for machine learning algorithms which
makes system learn from previous experiences
2

3. Objective
• Minimize makespan of Grid System
• Makespan is used to measure the throughput of the grid
system.
• Makespan is the total completion time of a particular task on
a machine
3

4. Alternative solutions
• Grid scheduling algorithms such as
Opportunistic load balancing (OLB)
Maximum Standard deviation heuristic
• ANT COLONY OPTIMIZATION(ACO)
[1]
• ACO is a population based search optimization technique
developed in the year 1997
• This algorithm simulates a colony of artificial ants that behave
as cooperative agents where they are allowed to search and
reinforce pathways (solutions) in order to find the optimal
ones.
• This approach which is population based has been successfully
applied to many NP-hard optimization problems.
4

5. Algorithm
Step 1: Construct the ETC matrix
Step 2:Repeat steps 3 to 10
Step 3:Set all initial values
pheromone evapouration value ƿ = 0.5.
pheromone trail T0 = 0.01 (initial deposit)
Free(0 to m-1) = 0
k = any number of ants.
Step 4:For each ant do step 5 to 7.
Step 5:Select the <task,machine> pair randomly.
Step 6:Repeat following steps until all tasks are finished
(i) calcutate the heuristic function nhj.(0<h<i)
(ii) Assign higher probabilty to tasks that have high
standard deviation among tasks
(iii) calculate the probability matrix P for all machines m
5

6. Select the next <task,machine> pair according to the
probablitiy matix P.
Step 7: Find the Best Solution from the solutions of all ants.
Step 8:Update the pheromone trail.
Step 9:Compare the previous sloution with the current solution
and save the better solution.
6

7. Comparison of ACO with other
scheduling algorithms.
7

8. Proposed solution
Avoid Local optimum problem.
Solution is to implement multiple Ant colonies .
Update the pheromone value taking average of all colonies.
Extending job onto Online Environment.
• Each job is charecterized by a set of attributes.
• A job can be classified by following attributes.
• Number of reads.
• Number of writes.
• Classify the jobs according to the attibutes into particular classes.
• Train the scheduler with the training data.
• The scheduler will classify the job to the machine which the
classifier have mapped onto.
8

9. Feasibility study
• The jobs are classified onto appropriate machine using
read and write operations per job,using machine learning tool
WEKA.
• Using the excel based tool SOLVER ,training data set is given
as input .
•
Constraint is given as ∑min(makespan).
•
New testing data classfied automatically.
• Neural networks can also be used for classification.
9

10. Conclusion
• Grid scheduling can be implemented within Polynomial time
by adopting machine learning algorithms.
• ACO algorithm performs better than traditional scheduling
algorithms.
• The scheduling can be extended onto an online environment
by applying suitable classification algorithms.
10

11. References
• [1].Ant Colony System: A Cooperative Learning Approach to the
Salesman Problem , Marco Dorigo,IEEE 1997
Traveling
• [2].An Improved Ant Algorithm for Grid Scheduling Problem,
Bagherzadeh, Mojtaba MadadyarAdeh,IEEE 2009
Jamshid
• [3].Task Scheduling with Load Balancing using Multiple Ant Colonies Optimization
in Grid Computing, Liang Bai, Yan-Li Hu, Song-Yang Lao, Wei-Ming Zhang,2010
IEEE
• [4].A Task scheduling for grid scheduling using Ant colony Optimization,Jun
Mao,IEEE 2011
• [5].Evaluating Scheduling Algorithms on Distributed
Ryan J. Wisnesky
Computational Grids,
• [6] Improved job grouping based PSO algorithm for task scheduling in grid
computing,Sudha sadhasivam,IJEST 2010
• [7] Wikipedia-Particle Swarm optimization.
11